Redis缓存设计与性能优化
多级缓存架构
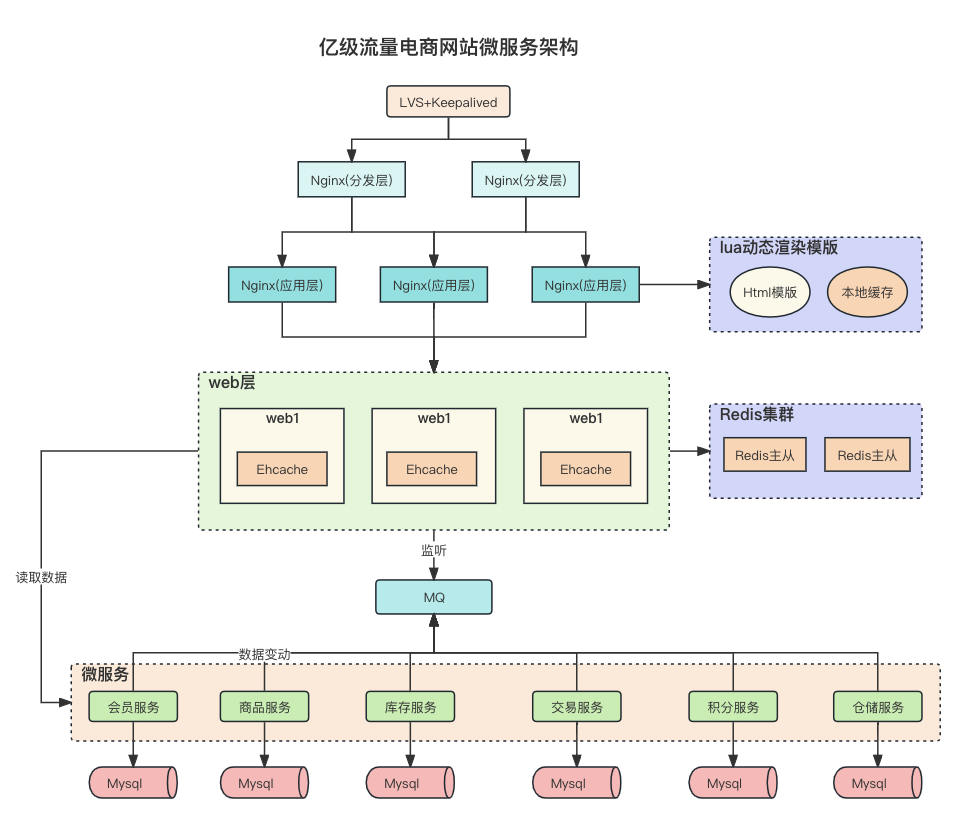
缓存设计
缓存穿透
- 缓存穿透是指查询一个根本不存在的数据, 缓存层和存储层都不会命中, 通常出于容错的考虑, 如果从存储层查不到数据则不写入缓存层。
- 缓存穿透将导致不存在的数据每次请求都要到存储层去查询, 失去了缓存保护后端存储的意义。
造成缓存穿透的基本原因有两个:
- 自身业务代码或者数据出现问题。
- 一些恶意攻击、 爬虫等造成大量空命中。
缓存穿透问题解决方案:
1、缓存空对象
String get(String key) {// 从缓存中获取数据String cacheValue = cache.get(key);// 缓存为空if (StringUtils.isBlank(cacheValue)) {// 从存储中获取String storageValue = storage.get(key);cache.set(key, storageValue);// 如果存储数据为空, 需要设置一个过期时间(300秒)if (storageValue == null) {cache.expire(key, 60 * 5);}return storageValue;} else {// 缓存非空return cacheValue;}
}
相关文章:

Redis缓存设计与性能优化
多级缓存架构 缓存设计 缓存穿透 缓存穿透是指查询一个根本不存在的数据, 缓存层和存储层都不会命中, 通常出于容错的考虑, 如果从存储层查不到数据则不写入缓存层。缓存穿透将导致不存在的数据每次请求都要到存储层去查询, 失去…...
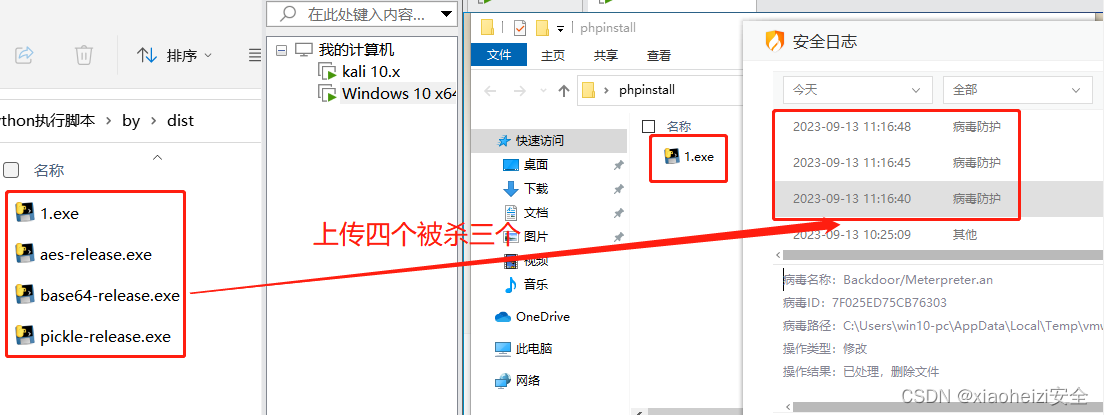
免杀对抗-Python-混淆算法+反序列化-打包生成器-Pyinstall
Python-MSF/CS生成shellcode-上线 cs上线 1.生成shellcode-c或者python 2.打开pycharm工具,创建一个py文件,将原生态执行代码复制进去 shellcode执行代码: import ctypesfrom django.contrib.gis import ptr#cs#shellcodebytearray(b"生…...

C#__线程池的简单介绍和使用
/*线程池原理:(有备无患的默认备用后台线程)特点:线程提前建好在线程池;只能用于运行时间较短的线程。*/class Program{static void Main(string[] args){for (int i 0; i < 10; i){ThreadPool.QueueUserWorkItem(Download); …...
)
安全员(岗位职责)
一、 安全员 是工程项目安全生产、文明施工的直接管理者和责任人,在业务上向 公司 负责; 二、贯彻安全条例和文明施工标准是安全员 工作 准则,执行相关规章、规程是安全员的责任; 三、办理开工前安全监审和安全开工审批,编制项目工程安全监督计划,上报安全措施和分项工程安全施…...
unity 使用声网(Agora)实现语音通话
第一步、先申请一个声网账号 [Agora官网链接](https://console.shengwang.cn/) 第二步在官网创建项目 ,选择无证书模式,证书模式需要tokenh和Appld才能通话 第三步 官网下载SDK 然后导入到unity,也可以直接在unity商店…...
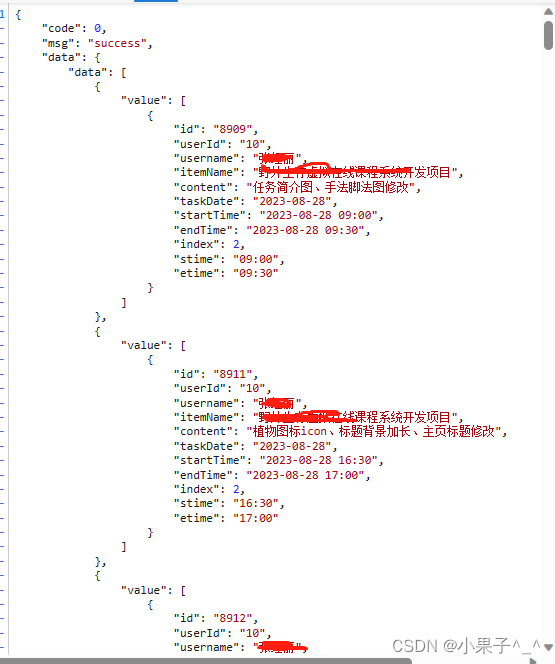
vue2.X 中使用 echarts5.4.0实现项目进度甘特图
vue2.X 中使用 echarts5.4.0实现项目进度甘特图 效果图: 左侧都是名称,上面是时间,当中的内容是日志内容 组件: gantt.vue <template><div id"main" style"width: 100%; height: 100%"></…...

《PostgreSQL与NoSQL:合作与竞争的关系》
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🐅🐾猫头虎建议程序员必备技术栈一览表📖: 🛠️ 全栈技术 Full Stack: 📚…...

【FAQ】视频监控管理平台/视频汇聚平台EasyCVR安全检查相关问题及解决方法3.0
智能视频监控系统/视频云存储/集中存储/视频汇聚平台EasyCVR具备视频融合汇聚能力,作为安防视频监控综合管理平台,它支持多协议接入、多格式视频流分发,视频监控综合管理平台EasyCVR支持海量视频汇聚管理,可应用在多样化的场景上&…...

Java 8 新特性解读及应用实践
Java 8 新特性解读及应用实践 一、简介二、Lambda表达式三、流式编程四、日期/时间API1. 概述2. LocalDate、LocalTime、LocalDateTime等类的使用3. 格式化与解析 五、重复注解和类型注解1. 概念与作用2. 重复注解实例3. 类型注解实例 六、小结回顾 一、简介 Java 8带来了众多…...

C++项目实战——基于多设计模式下的同步异步日志系统-④-日志系统框架设计
文章目录 专栏导读模块划分日志等级模块日志消息模块日志消息格式化模块日志消息落地模块日志器模块日志器管理模块异步线程模块 模块关系图 专栏导读 🌸作者简介:花想云 ,在读本科生一枚,C/C领域新星创作者,新星计划导…...

计算机专业毕业设计项目推荐02-个人医疗系统(Java+原生Js+Mysql)
个人医疗系统(Java原生JsMysql) **介绍****系统总体开发情况-功能模块****各部分模块实现** 介绍 本系列(后期可能博主会统一为专栏)博文献给即将毕业的计算机专业同学们,因为博主自身本科和硕士也是科班出生,所以也比较了解计算机专业的毕业设计流程以…...

Nginx__高级进阶篇之LNMP动态网站环境部署
动态网站和LNMP(LinuxNginxMySQLPHP)都是用于建立和运行 web 应用程序的技术。 动态网站是通过服务器端脚本语言(如 PHP、Python、Ruby等)动态生成网页内容的网站。通过这种方式,动态网站可以根据用户的不同请求生成不…...

Zebec 生态 AMA 回顾:Nautilus 以及 $ZBC 的未来
在9月7日,Zebec创始人Sam做客社区,并进行了“Nautilus Chain以及$ZBC的未来”主题的AMA访谈。Sam在本次访谈中对Nautilus Chain生态的价值捕获、Zebec生态布局规划、可能会推出的Nautilus Chain治理通证NAUT进行了解读。本文将对本次AMA进行回顾与总结。…...

NXP iMX8MM 修改 UART4至 Cortex-A53 核心
By Toradex秦海 1). 简介 NXP iMX8MM SoC UART-4 接口在默认的 ATF(ARM Trusted Firmware) 中被 RDC 分配给了 Cortex-M4 核心,用作 M4 核心的 Debug UART。如果这时候在 Cortex-A53 核心 Linux Devcie-tree 配置中使能 UART-4,就会出现 Kernel Oops 错…...
C#控制台程序中使用log4.net来输出日志
Apache log4net 库是一个帮助程序员将日志语句输出到各种输出目标的工具。log4net 是优秀的 Apache log4j™ 框架到 Microsoft .NET 运行时的端口。 我喜欢他可以自定义输出,区分等级等特点。 导入库 我们在工程里添加NuGet的包。输入名称log4net ࿰…...

用GPT干的18件事,能够真正提高学习生产力,建议收藏
用GPT干的18件事,能够真正提高学习生产力,建议收藏。 语法更正 文本翻译 语言转换 代码解释 修复代码错误 作为百科全书 信息提取 好友聊天 创意生成器 采访问题 论文大纲 故事创作 问题类比 创建 SQL 需求 情感分析 将产品描述转变为广告 关键字提取 闲…...

线性代数的本质(二)——线性变换与矩阵
文章目录 线性变换与矩阵线性变换与二阶方阵常见的线性变换复合变换与矩阵乘法矩阵的定义列空间与基矩阵的秩逆变换与逆矩阵 线性变换与矩阵 线性变换与二阶方阵 本节从二维平面出发学习线性代数。通常选用平面坐标系 O x y Oxy Oxy ,基向量为 i , j \mathbf i,…...

JavaScript获取字符串的字节长度
概要 提示:大家都知道,获取字符串的长度可用length来获取。 那么获取这段字符串的字节数呢?英文字母肯定lenght和字节数都一样:都是1而中文lenght1,字节数2因此,需要作的就是把中文字符的字节数计算出来。 …...

[2023.09.13]: Rust Lang,避不开的所有权问题
Rust的所有权问题,在我学Rust的时候就跳过了,因为我知道这玩意儿没有场景就不好理解。没想到场景很快就出现了。 在开发Yew应用组件的时候,涉及到了事件,闭包,自然就引出了所有权问题。 话不多说,下面让我们…...
Redux中间件源码解析与实现
基本介绍 本文中涉及到的关键npm包的版本信息如下: react 的版本为18.2.0 redux的版本为4.1.2 redux-thunk版本为2.4.2 redux-promise版本为0.6.0 redux-logger版本为3.0.6 在Redux源码解析与实现(一)Redux源码解析与实现(二&…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...
