JavaScript获取字符串的字节长度
概要
提示:大家都知道,获取字符串的长度可用length来获取。 那么获取这段字符串的字节数呢?英文字母肯定lenght和字节数都一样:都是1而中文lenght=1,字节数=2因此,需要作的就是把中文字符的字节数计算出来。
例如:
let str = "abcd";
console.log(str.length) // 4
let str = "字符串";
console.log(str.length) // 3
提示:很显然这么获取字节长度是不对的。
实践
我们可以换一种思路,既然要求是获取字符串的字符长度,我们可以先把字符串直接转换成字节,然后直接获取字节的长度就可以了。
JavaScript如何将字符串转换为字节数组
方法:使用TextEncoder
TextEncoder() 构造函数总是返回一个新创建的 TextEncoder 对象,该对象将生成具有 UTF-8 编码的字节流。TextEncoder 接口不继承任何属性。
TextEncoder是一个内置的API,可用于将字符串转换为字节数组。以下是使用TextEncoder的示例代码:
// js字符获取字节长度
let str = "/测试测试/test1.js"
let encoder = new TextEncoder();
let bytes = encoder.encode(str);
console.log(bytes.length) //22
上述代码中,我们首先创建一个TextEncoder实例,然后使用encode方法将字符串转换为字节数组。最后,我们通过控制台输出字节数组。请注意,TextEncoder是现代浏览器的标准API,因此在旧版本的浏览器中可能不可用。
相关文章:

JavaScript获取字符串的字节长度
概要 提示:大家都知道,获取字符串的长度可用length来获取。 那么获取这段字符串的字节数呢?英文字母肯定lenght和字节数都一样:都是1而中文lenght1,字节数2因此,需要作的就是把中文字符的字节数计算出来。 …...

[2023.09.13]: Rust Lang,避不开的所有权问题
Rust的所有权问题,在我学Rust的时候就跳过了,因为我知道这玩意儿没有场景就不好理解。没想到场景很快就出现了。 在开发Yew应用组件的时候,涉及到了事件,闭包,自然就引出了所有权问题。 话不多说,下面让我们…...
Redux中间件源码解析与实现
基本介绍 本文中涉及到的关键npm包的版本信息如下: react 的版本为18.2.0 redux的版本为4.1.2 redux-thunk版本为2.4.2 redux-promise版本为0.6.0 redux-logger版本为3.0.6 在Redux源码解析与实现(一)Redux源码解析与实现(二&…...

关于rsync用不了之后
1.尝试找出rsync使用错误原因: 我遇见一个问题:rsync:read errors mapping:communication error on send (70),我查了一下这个问题很大可能是网络链接导致的,然后我用nslookup指令查看了/train2…...

由一个多线程并发保存而引发的思考
1. 问题描述 问题描述,现A表(用户查看实验的次数)有user_id和exp_id两个字段,其中user_id加exp_id不唯一。B表有user_id,exp_id以及exp_num三个字段,其中user_id加exp_id唯一(表中未建唯一索引)。 现需要将A表的数据同步到B表,单机模式通过定时任务同步。A表的数据有…...

python-vlc
文章目录 关于 python-vlc安装使用关于 python-vlc Python vlc bindings github : https://github.com/oaubert/python-vlcPython bindings (ctypes-based) for VLC http://olivieraubert.net/vlc/python-ctypes/关于 VLC 可参考 macOS - 安装使用 VLC https://blog.csdn.net/…...
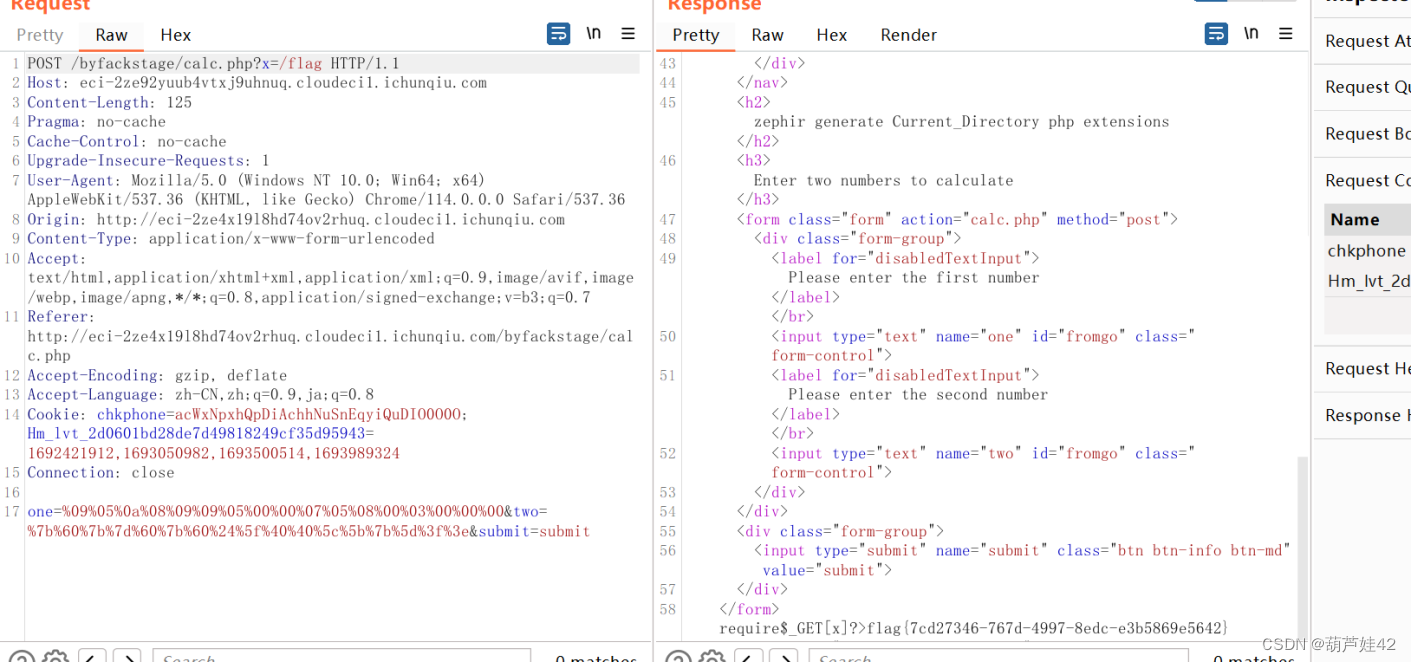
2023长城杯 web部分题目(seekingeasy_extension)
seeking 下载题目附件得到: <?php error_reporting(0); header("HINT:POST n range(1,10)");$image $_GET[image]; echo "这里什么也没有,或许吧。"; $allow range(1, 10); shuffle($allow); if (($_POST[n] $allow[0])) …...
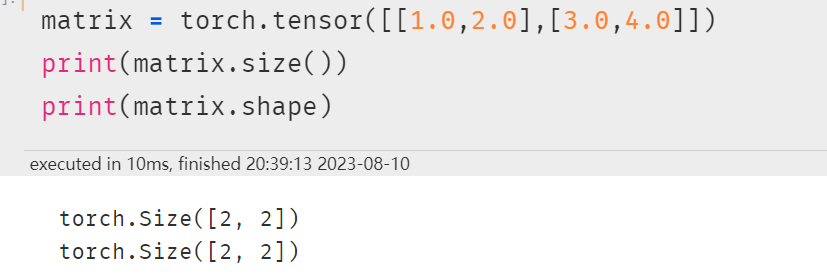
2-1 张量数据结构
张量概念 张量是什么? 单个元素叫标量(scalar),一个序列叫向量(vector),多个序列组成的平面叫矩阵(matrix),多个平面组成的立方体叫张量(tensor&…...

QSqlQuery查询语句
SqlQuery 封装了在 QSqlDatabase 上执行的 SQL 查询中创建、导航和检索数据所涉及的功能。 可用于执行 DML(数据操作语言)语句,如 SELECT、INSERT、UPDATE 和 DELETE, 以及 DDL(数据定义语言)语句ÿ…...
用c语言编写出三底模型
以下是一个用C语言实现三底模型的示例代码。这个程序通过循环遍历输入的股票数据,判断是否出现三底形态,如果是,则输出买入信号,否则输出卖出信号。 c语言 #include <stdio.h> #include <stdlib.h> // 判断是否出现…...

15 Python使用MySQL
概述 在上一节,我们介绍了如何在Python中使用网络,包括:套接字编程、socketserver等内容。在这一节,我们将介绍如何在Python中使用MySQL。MySQL是最流行的关系型数据库管理系统之一,由瑞典MySQL AB公司开发,…...

3、Nginx 常用的命令和配置文件
文章目录 3、nginx 常用的命令和配置文件3.1 nginx 常用的命令:3.2 nginx.conf 配置文件3.2.1 地址3.2.2 内容3.2.2 vim不正常退出后再次打开信息提示解决方法 3.3 第一部分:全局块3.4 第二部分:events 块3.4 第三部分:http 块①、…...

python经典百题之兔子出生问题
这是一个经典的 Fibonacci 数列问题,可以通过递归或循环来解决。 递归方法: 由题意可知,第 n 个月的兔子数等于第 n-1 个月的兔子数加上第 n-2 个月的兔子数。设 f(n) 表示第 n 个月的兔子数,则有: f(n) f(n-1) f…...

不定积分的概念和性质
目录 原函数 不定积分 不定积分的几何意义 原函数的存在定理 不定积分的性质 不定积分是微积分的一个关键部分,它涉及到一个函数的不定积分的计算。不定积分可以理解为求一个函数的原函数,也被称为反导数。原函数是一个函数,使得该函数的…...

远程访问服务器JupyterLab的配置方法
远程访问服务器JupyterLab的配置方法 环境及工具注意 基本步骤生成密码生成并修改配置文件*错误:jupyter localhost 已拒绝连接*后台运行jupyter后台关闭 其实就是在服务器运行JupyterLab,然后在本地浏览器访问 环境及工具 服务器:Ubuntu 1…...
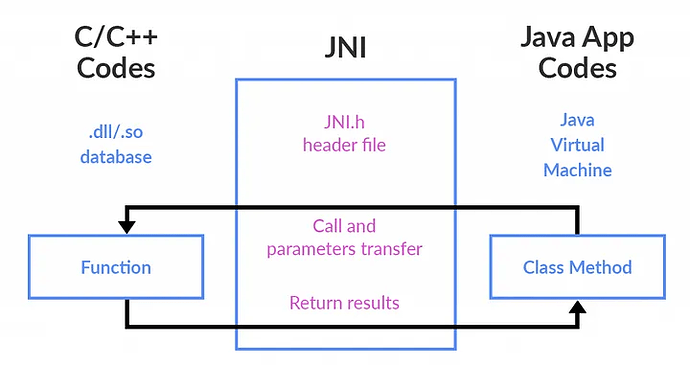
Java native 关键字
如你在看 JDK 的源代码的时候,大概率会看到很多方法使用了 native 关键字。 下面是 String 对象 JDK 中的源代码,就带有了一个 native 关键字。 native 是干什么用的 简单来说就是 Java 的 native 方法的实现不是用 Java 实现的,可能在其他…...
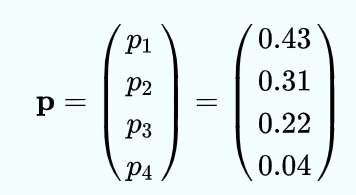
【线性代数】沉浸式线性代数在线学习网站
地址:http://immersivemath.com/ila/index.html 这是全球第一本带交互式图形的线性代数教材,作者是 J. Strm, K. strm, and T. Akenine-Mller。 全书一共十章,各章节内容如下: 接下来我将对各章节进行简单的总结,另外…...

Kotlin中特性、数据类、伴生对象、顶层函数
Kotlin中的函数参数和属性声明 在 Kotlin 中,函数参数和属性有不同的声明方式和行为。这些特性使得 Kotlin 代码更加安全、易于理解和维护。 函数参数的只读性 fun sum(a: Int, b: Int): Int {var modifiedA aif (modifiedA > 0) {modifiedA 1}//三元表达式v…...

《PostgreSQL物化视图:创建、维护与应用》
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🐅🐾猫头虎建议程序员必备技术栈一览表📖: 🛠️ 全栈技术 Full Stack: 📚…...

shell脚本之test命令
shell脚本之test命令 数值比较:2. 字符串比较:3. 文件测试:4. 逻辑操作:5. 其他测试: test命令在Shell脚本中用于进行条件测试和条件判断。它用于检查文件、字符串和数值的各种条件,并返回一个状态码&#…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
