jdk 中的 keytool 的使用,以及提取 jks 文件中的公钥和私钥
这里暂时只需要知道如何使用就可以了。
首先是生成一个密钥,
keytool -genkeypair -alias fanyfull -keypass ffkp123456 -validity 365 -storepass ffsp123456 -keystore fanyfull.jks -keyalg RSA
解释一下这里的选项,
- -alias 密钥对的名称
- -keypass 密钥密码
- -validity 有效期,这里是以天为单位
- -storepass 存储库的密码
- -keystore 指定生成的密钥文件存放的位置,这里的
fanyfull.jks表示的是当前目录下的fanyfull.jks,如果没有,就生成这个文件 - -keyalg 指定这个密钥对生成的算法,这里用的是 RSA 算法
如果想查看生成的 jks 文件的详细信息,可以使用以下命令,
keytool -list -v -alias fanyfull -storepass ffsp123456 -keystore .\fanyfull.jks
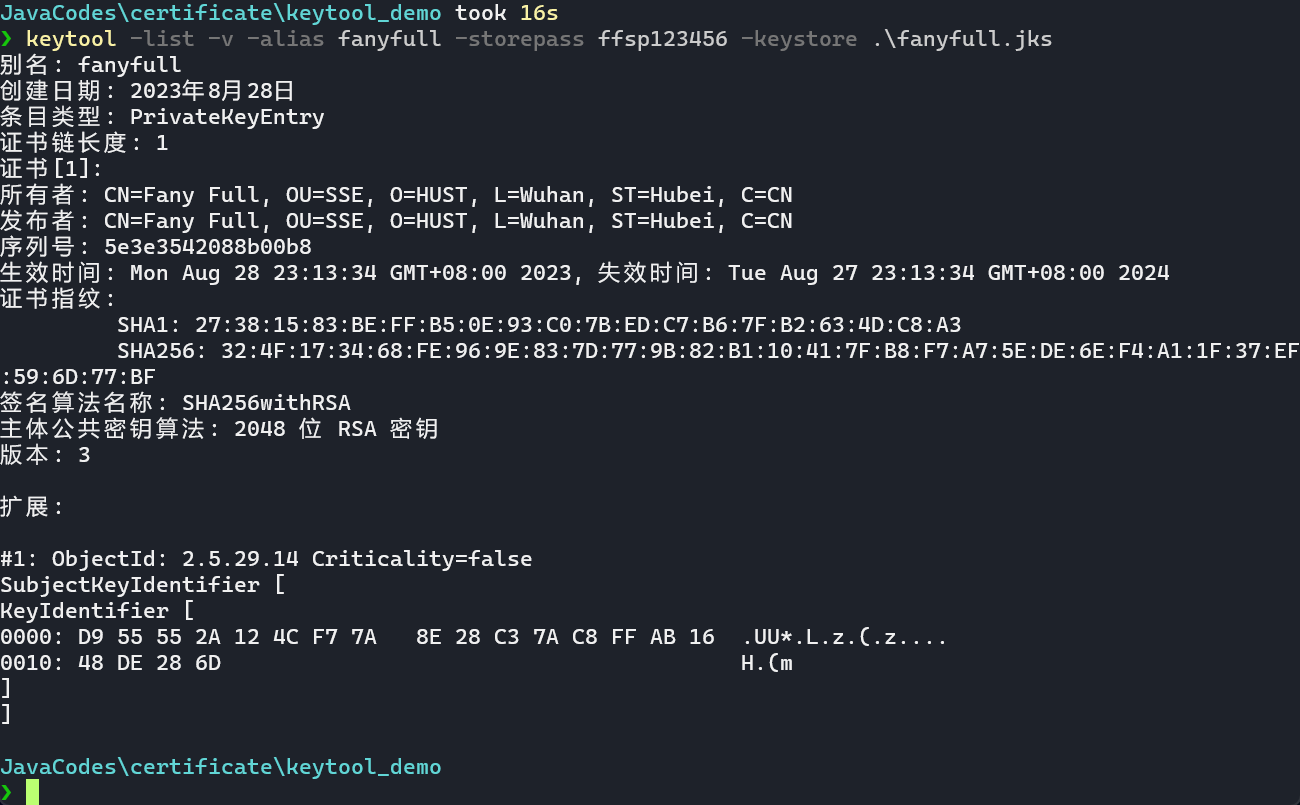
然后是提取私钥,
keytool -importkeystore -srckeystore .\fanyfull.jks -destkeystore fanyfull.p12 -deststoretype PKCS12 -srcalias fanyfull -deststorepass ffsp123456 -destkeypass ffkp123456
然后根据提示输入 storepass 即可,

然后,可以使用 openssl 工具来提取其中的私钥,
openssl pkcs12 -nodes -in .\fanyfull.p12 -out private.pem
我们可以查看一下这里的私钥,
这里的 BEGIN PRIVATE KEY 和 END PRIVATE KEY 之间的内容就是我们的私钥。
然后是提取公钥,
openssl pkey -in .\private.pem -pubout -out public.pem
我们可以查看一下这里的公钥,
这里的 BEGIN PUBLIC KEY 和 END PUBLIC KEY 之间的内容就是我们的私钥。
而,如果我们单纯地只是想提取证书的话,那么,可以使用以下的命令,
keytool -export -alias fanyfull -keystore .\fanyfull.jks -file public.cert -rfc相关文章:

jdk 中的 keytool 的使用,以及提取 jks 文件中的公钥和私钥
这里暂时只需要知道如何使用就可以了。 首先是生成一个密钥, keytool -genkeypair -alias fanyfull -keypass ffkp123456 -validity 365 -storepass ffsp123456 -keystore fanyfull.jks -keyalg RSA解释一下这里的选项, -alias 密钥对的名称-keypass …...
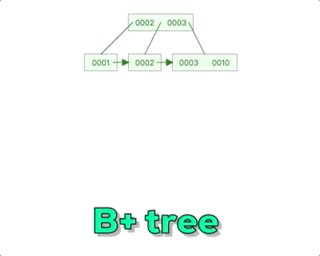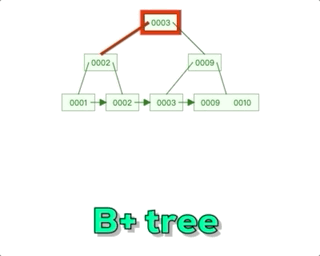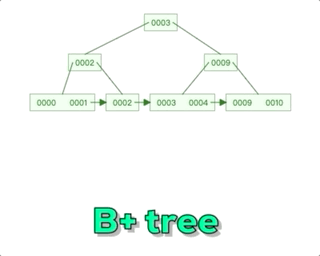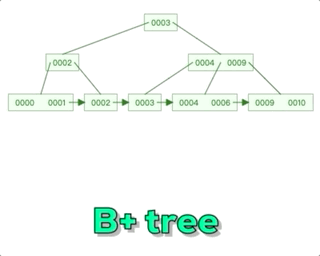
Mysql--技术文档--B+树-数据结构的认知
阿丹解读: 之前的文章中写道了有关mysql底层索引,那么在数据量特别大的情况下。mysql采用了B来管理索引。和存储的数据。 Mysql--技术文档--索引-《索引为什么查找数据快?》-超底层详细说明索引_一单成的博客-CSDN博客 B树解读:…...
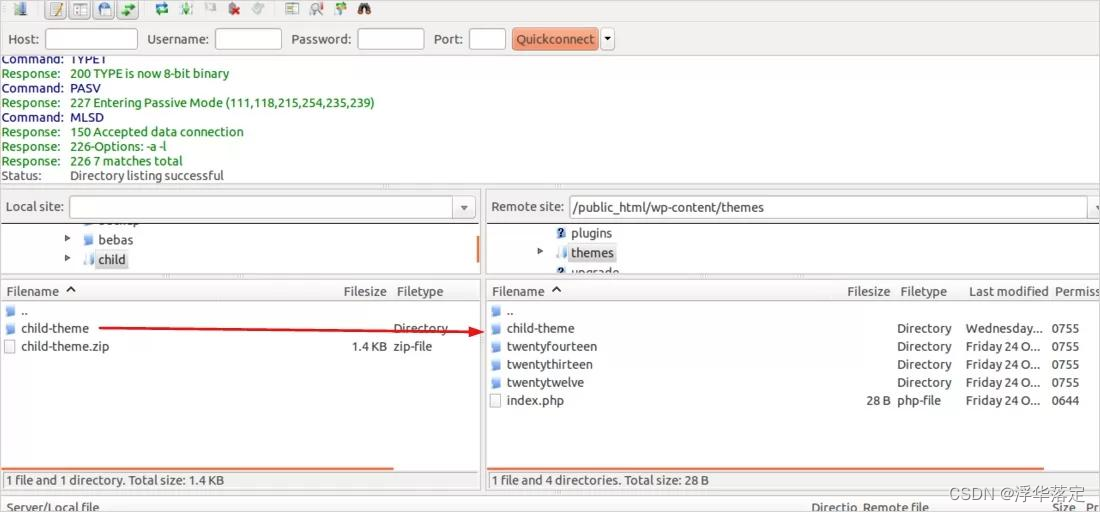
cms之wordpress主题安装
WordPress主题安装教程的方法有两种,分为在线安装和上传安装,下面是主题详细安装方法的步骤。 后台在线安装主题 从后台的主题界面在线安装主题是最方便的WordPress主题安装方式。方法如下: 1 在WordPress后台,转到外观→主题 …...
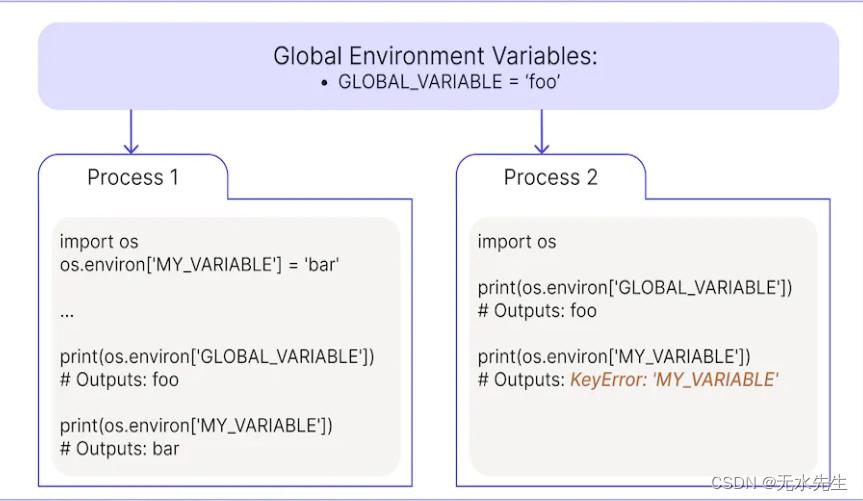
【Python程序设计】Python 中的环境变量【05/8】
一、说明 以下文章是有关 Python 数据工程系列文章的一部分,旨在帮助数据工程师、数据科学家、数据分析师、机器学习工程师或其他刚接触 Python 的人掌握基础知识。本篇将讲述环境变量的问题。 迄今为止,本初学者指南包括: 第 1 部分…...
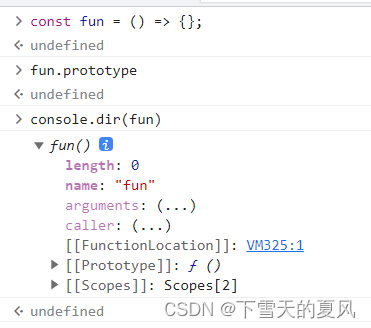
查漏补缺 - ES6
目录 1,let 和 const1,会产生块级作用域。2,如何理解 const 定义的变量不可被修改? 2,数组3,对象1,Object.is()2,属性描述符3,常用API4,得到除某个属性之外的新对象。 4…...
:最初的项目思路(SLAM))
基于视觉重定位的室内AR导航APP的大创项目思路(1):最初的项目思路(SLAM)
文章目录 最初的项目思路(SLAM):后文: 前情提要: 是第一次做项目的小白,文章内的资料介绍如有错误,请多包含! 最初的项目思路(SLAM): 由于我们在…...
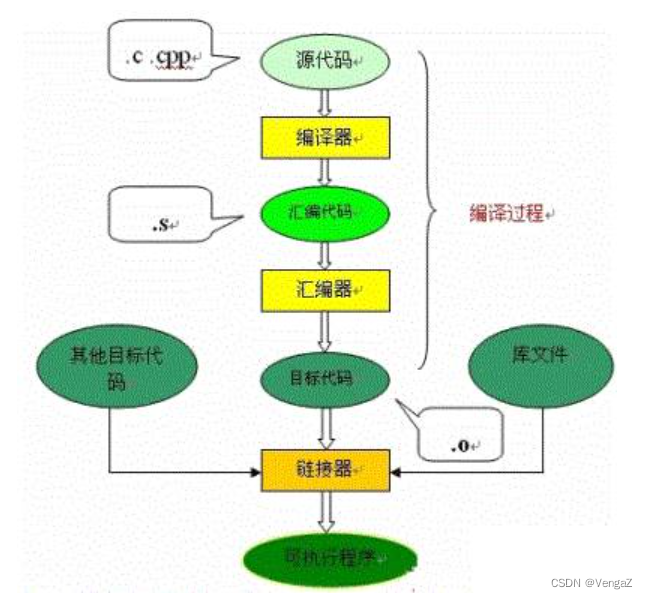
C 编译原理
C 编译原理 目录 C 编译原理引入GCC 工具链介绍C运行库 编译准备工作编译过程1.预处理2.编译3.汇编4.链接 分析ELF文件1.ELF文件的段2.反汇编ELF C语言编译过程 - 摘录编译预处理编译、优化汇编链接过程 引入 大家肯定都知道计算机程序设计语言通常分为机器语言、汇编语言和高…...

服务管理工具systemctl
服务管理工具systemctl Linux服务管理两种方式 service 和 systemctl systemd 是Linux系统最新的初始化系统(init),作用是提高系统的启动速度,尽可能启动较少的进程,尽可能更多进程并发启动. systemd 对应的进程管理命令是systemctlsystemctl 是systemd的主命令,用于管理系统…...
Spring boot环境搭建
使用IDE工具:IntelliJ IDEA 目录 一、安装JAVA 二、安装maven(Java项目管理工具) 三、安装IDE 四、在IDE中配置spring boot项目环境 1、配置jdk 2、配置maven 3、安装创建spring boot项目插件:Spring Assistant 4、安装简…...

【C++】list的模拟实现【完整理解版】
目录 一、list的概念引入 1、vector与list的对比 2、关于struct和class的使用 3、list的迭代器失效问题 二、list的模拟实现 1、list三个基本函数类 2、list的结点类的实现 3、list的迭代器类的实现 3.1 基本框架 3.2构造函数 3.3 operator* 3.4 operator-> 3…...
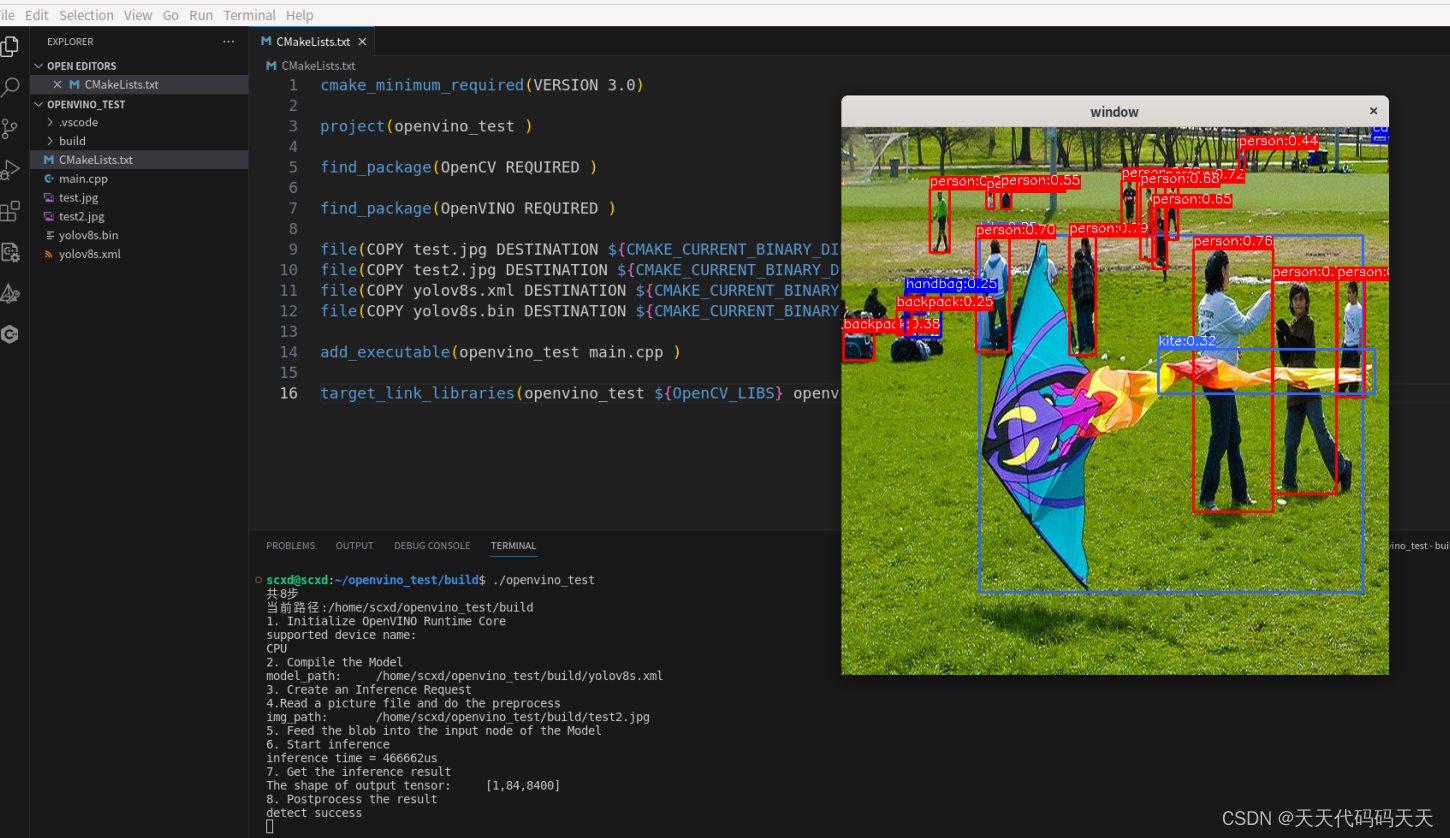
Linux C++ OpenVINO 物体检测 Demo
目录 main.cpp #include <iostream> #include <string> #include <vector> #include <openvino/openvino.hpp> #include <opencv2/opencv.hpp> #include <dirent.h> #include <stdio.h> #include <time.h> #include …...

解决运行Docker镜像报错:version `GLIBC_2.32‘ not found
解决运行Docker镜像,报错:version GLIBC_2.32’ not found 详细报错日志 xapi-backend % docker logs 036de55b5bc6 ./xapi-backend: /lib/aarch64-linux-gnu/libc.so.6: version GLIBC_2.32 not found (required by ./xapi-backend) ./xapi-backend: …...

网络层--IP协议
引入: IP协议主要解决什么问题呢? IP协议提供一种将数据从主机A 发送到 主机B的能力。(有能力不一定能做到,比如小明很聪明,可以考100分,但是他也不是每次搜能考100分࿰…...
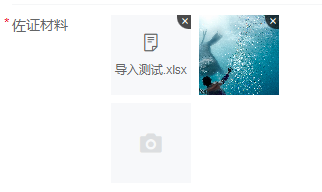
Vue2 | Vant uploader实现上传文件和图片
需求: 实现图片和文件的上传,单个图片超过1M则压缩,全部文件加起来不得超过10M。 效果: 1. html <van-form ref"form"><van-field name"uploader" label"佐证材料" required><t…...

第二十一章 Classes
文章目录 第二十一章 ClassesClasses类名和包类定义的基本内容 第二十一章 Classes Classes 类定义并不是 ObjectScript 的正式组成部分。相反,可以在类定义的特定部分中使用 ObjectScript(特别是在方法定义中,可以在其中使用其他实现语言&…...

Ubuntu不能上网解决办法
问题及现象 Ubuntu的虚拟机(18.04)总是莫名就不能上网了。 使用ifconfig -a 查看,ensxx(xx为虚拟机分配的id号)对应的网卡有mac地址,但是没有分配ip地址。 Network中也没有Wired的选项。 临时解决方案 使…...
百度飞浆OCR识别表格入门python实践
1. 百度飞桨(PaddlePaddle) 百度飞桨(PaddlePaddle)是百度推出的一款深度学习平台,旨在为开发者提供强大的深度学习框架和工具。飞桨提供了包括OCR(光学字符识别)在内的多种功能,可…...

直接插入排序、希尔排序详解。及性能比较
直接插入排序、希尔排序详解。及性能比较 一、 直接插入排序1.1 插入排序原理1.2 代码实现1.3 直接插入排序特点总结 二、希尔排序 ( 缩小增量排序 )2.1 希尔排序原理2.2 代码实现2.3 希尔排序特点总结 三、直接插入排序和希尔排序性能大比拼 !!!3.1 如何对比性能?准…...

2023备战秋招Java面试八股文合集
Java就业大环境仍然根基稳定,市场上有很多机会,技术好的人前景就好,就看你有多大本事了。小编得到了一份很不错的资源,建议大家可以认真地来看看以下的资料,来提升一下自己的核心竞争力,在面试中轻松应对面…...

SLAM中的二进制词袋生成过程和工作原理
长期视觉SLAM (Simultaneous Localization and Mapping)最重要的要求之一是鲁棒的位置识别。经过一段探索期后,当长时间未观测到的区域重新观测时,标准匹配算法失效。 当它们被健壮地检测到时,回环检测提供正确的数据关联以获得一致的地图。…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
