递归学习——记忆化搜索
目录
编辑
一,概念和效果
二,题目
1.斐波那契数
1.题目
2.题目接口
3.解题思路
2.不同的路径
1.题目
2.题目接口
3.解题思路
3.最长增长子序列
1.题目
2.题目接口
3.解题思路
4.猜数字游戏II
1.题目
2.题目接口
3.解题思路
总结:
一,概念和效果
记忆化搜索可以说是带备忘录的递归,实现这个算法的目的便是减少递归时对同一个节点的多次遍历从而提高学习效率。学习这个算法,理解这个算法最好的方式便是通过能够用记忆化搜索的题目来理解。
二,题目
1.斐波那契数
1.题目
斐波那契数 (通常用
F(n)表示)形成的序列称为 斐波那契数列 。该数列由0和1开始,后面的每一项数字都是前面两项数字的和。也就是:F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1给定
n,请计算F(n)。
2.题目接口
class Solution {
public:int fib(int n) {}
};3.解题思路
相信大家都知道如何解决斐波那契数的问题。这个问题的经典解决方式便是运用到递归解法。使用递归时要明确的便是递归的出口。斐波那契数的递归出口便是在n == 0或者n==1时。这两个条件下的返回值便是它们本身。当n不等于0和1时f(n) = f(n-1)+f(n-2)条件成立。
根据以上思路便可以写出如下解题代码:
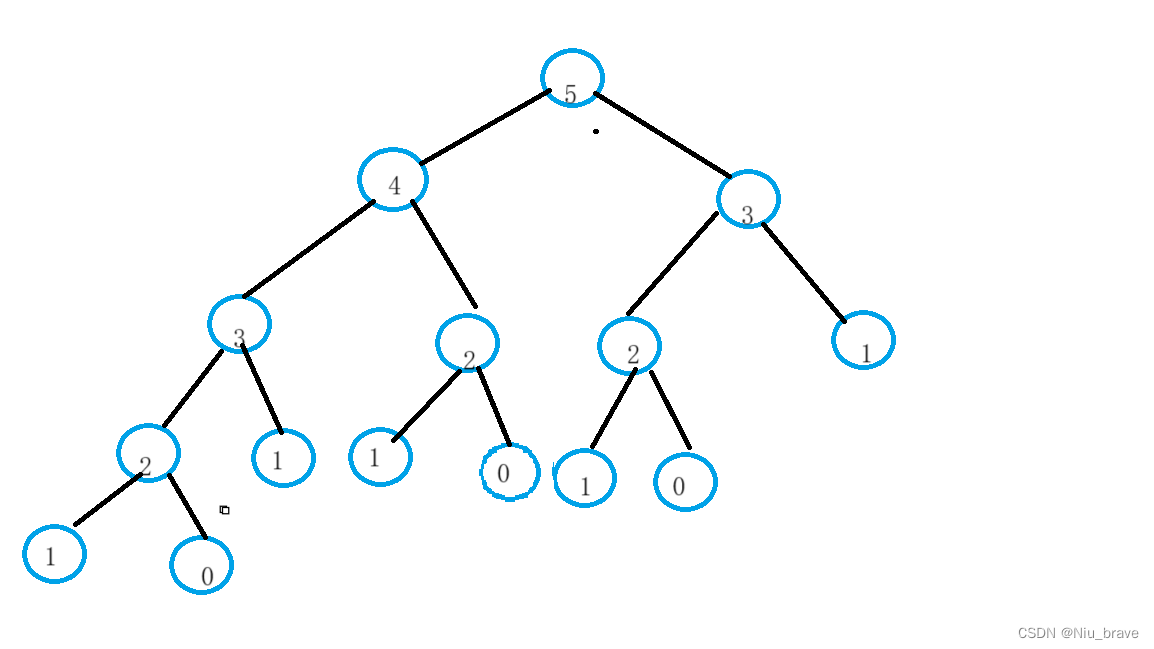
class Solution { public:int fib(int n) {return dfs(n);}int dfs(int n){if(n == 0||n == 1){return n;}return dfs(n-1)+dfs(n-2);} };但是我们都知道在递归时会有大量的重复计算。比如当n == 5时递归展开图如下:
在这里可以看到2这个节点被求了很多次,这样子便是很大的浪费了。这个时候为了提高效率便可以采用记忆化搜索的方式。记忆化搜索的实现其实也非常的简单,也就是当我们得到一个结果时便将其记录下来。当我们想要再次遍历相同的节点时只要看前面是否有记录过,若记录过便不再访问直接返回之前记录过的结果就行了。比如斐波那契数列这道题的记忆化搜索方式的解题代码如下:
class Solution { public:vector<int>memo;//表示备忘录int fib(int n) {memo = vector<int>(n+1);//初始化return dfs(n);}int dfs(int n){if(n == 0||n == 1){return n;}if(memo[n]!=0)//册中已求便无需再求{return memo[n];}memo[n] = dfs(n-1)+dfs(n-2);//记录在册return memo[n];} };
2.不同的路径
1.题目
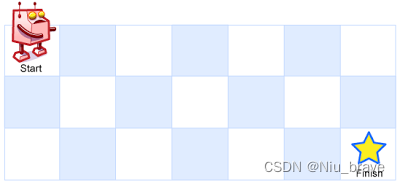
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
2.题目接口
class Solution {
public:int uniquePaths(int m, int n) {}
};3.解题思路
因为机器人只能向前或者向下走,所以要到达finish位置的话首先就要到达finish的上面和左边这两个位置:
要到达这两个位置的话便又要到达这两个位置的上面和下面位置。以次类推得到公式:
f(finishi,finishj) = f(finishi-1,finishj)+f(finishi,finishj-1)。得到这个关系我们便可以知道这道题和斐波那契数列有的一拼,所以自然就会想到递归的解法。在这里便要寻找递归条件了。
1.因为目中给的m与n表示的是网格的长与宽。所以当m == 1&&n == 1时就意味着网格里面只有一个格子,也就是机器人就在右下角的格子了所以返回1。
2.当给的m与n中有一个为0的话,也就是网格的长或者宽为0,也就表示没有格子于是返回0。
根据以上分析写出代码如下:
class Solution { public:int uniquePaths(int m, int n) {return dfs(m,n);} int dfs(int m,int n){if(m == 1&&n==1){return 1;}if(m ==0||n==0){return 0;}return dfs(m-1,n)+dfs(m,n-1);} };
但是这个代码会超时,所以我们得优化这个代码让这个代码变得更快。优化的方式便是记忆化搜索:
class Solution { public:vector<vector<int>>memo;int uniquePaths(int m, int n) {memo = vector<vector<int>>(m+1,vector<int>(n+1));return dfs(m,n);} int dfs(int m,int n){if(memo[m][n]!=0){return memo[m][n];}if(m == 1&&n==1){return 1;}if(m ==0||n==0){return 0;}memo[m][n] = dfs(m-1,n)+dfs(m,n-1);return memo[m][n];} };
可以看到这道题的记忆化搜索处理方式和上一道题一毛一样。
3.最长增长子序列
1.题目
给你一个整数数组
nums,找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,
[3,6,2,7]是数组[0,3,1,6,2,2,7]的子序列。
2.题目接口
class Solution {
public:int lengthOfLIS(vector<int>& nums) {}
};3.解题思路
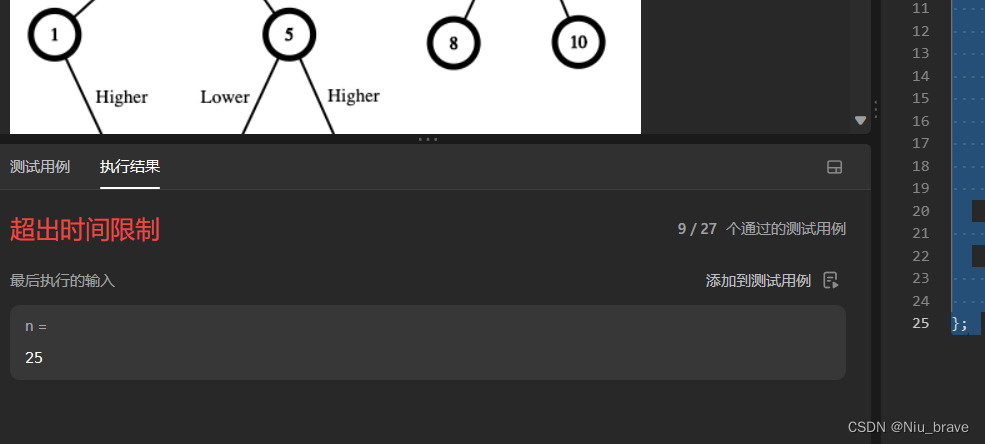
这道题的解题思路其实也不太难,就是要遍历一下每一个下标然后求出以每一个下标的起点为开始位置的子序列长度。但是因为我们要求的是最大长度所以需要比较更新最大长度。以这个思路写成代码如下:
class Solution { public:int len; int lengthOfLIS(vector<int>& nums) {len = nums.size();int ret = 0;for(int i = 0;i<len;i++){ret = max(ret,dfs(i,nums));//得到以某个下标为起点的最大长度} return ret;}int dfs(int i,vector<int>&nums){int ret = 1;//每一个子序列的最小长度为1for(int x =i+1;x<len;x++ ){if(nums[x]>nums[i]){ret = max(ret,dfs(x,nums)+1);//求出以每一个下标为起点的子序列长度,并每次都更新一下}}return ret;//返回最大值} };但是以上代码是通不过的,因为时间限制:
那该怎么办呢?其实很简单,还是和前两道题一样要采用一个记忆化搜索的策略:
class Solution { public:int len; vector<int>memo;int lengthOfLIS(vector<int>& nums) {len = nums.size();memo = vector<int>(len,1);int ret = 0;for(int i = 0;i<len;i++){ret = max(ret,dfs(i,nums));} return ret;}int dfs(int i,vector<int>&nums){if(memo[i]!=1)//判断一下{return memo[i];}int ret = 1;for(int x =i+1;x<len;x++ ){if(nums[x]>nums[i]){ret = max(ret,dfs(x,nums)+1);}}memo[i] = ret;//记录一下return ret;} };然后便过掉了:
4.猜数字游戏II
1.题目
我们正在玩一个猜数游戏,游戏规则如下:
- 我从
1到n之间选择一个数字。- 你来猜我选了哪个数字。
- 如果你猜到正确的数字,就会 赢得游戏 。
- 如果你猜错了,那么我会告诉你,我选的数字比你的 更大或者更小 ,并且你需要继续猜数。
- 每当你猜了数字
x并且猜错了的时候,你需要支付金额为x的现金。如果你花光了钱,就会 输掉游戏 。给你一个特定的数字
n,返回能够 确保你获胜 的最小现金数,不管我选择那个数字 。
2.题目接口
class Solution {
public:int getMoneyAmount(int n) {}
};3.解题思路
这道题该咋做呢?或者说这道题是什么意思呢?以输入一个数字10为例吧。我们要猜数字时便要在[1,10]之间猜测。于是我们猜数字策略便有很多种。比如一下几种:
1.当开始位置为1时
这里的至少要1+2+3+4+5+6+7+8块钱。
2.当我们一开始便选到5时:
还有一种便是这道题目给的最优解法:
在这个最优解法里边我们要做的便是找到这里的最大钱数也就是7+9 = 16。所以我们要做的便暴力搜索找出这个最优策略里的最大钱数。怎么做呢?其实还是遍历,抽象成下图:
这里一个一个试验的i便是为了得到最优模型而设计的。返回最大值便是为了得到每一个模型里面的最坏情况然后让每一个情况比较一下得到最优模型的最坏情况。写成代码如下:
class Solution { public:int getMoneyAmount(int n) {return dfs(1,n);}int dfs(int left,int right){if(left>=right)//当数组范围中只有一个数字或者范围不合法时便返回0。{return 0;}int ret = INT_MAX;//记录最优模型的最坏情况。for(int head = left;head<right;head++){int l = dfs(left,head-1)+head;//左结果int r = dfs(head+1,right)+head;//右结果ret = min(ret,max(l,r));//最优模型下的追怀情况}return ret;} };这样便得到了代码了,这个代码是对的但是遗憾的是这个代码过不了:
接下来采用记忆化搜索方式:
class Solution { public:vector<vector<int>>memo;int getMoneyAmount(int n) {memo = vector<vector<int>>(n+1,vector<int>(n+1));return dfs(1,n);}int dfs(int left,int right){if(memo[left][right]!=0){return memo[left][right];}if(left>=right){return 0;}int ret = INT_MAX;for(int head = left;head<right;head++){int l = dfs(left,head-1)+head;int r = dfs(head+1,right)+head;ret = min(ret,max(l,r));}memo[left][right] = ret;return ret;} };这样便可以过掉了:
总结:
其实记忆化搜索的目的便是实现剪枝操作,提高递归效率。当我们的递归操作里有大量的重复的递归操作时便可以用记忆化搜索的方式来提高递归效率。
相关文章:
递归学习——记忆化搜索
目录 编辑 一,概念和效果 二,题目 1.斐波那契数 1.题目 2.题目接口 3.解题思路 2.不同的路径 1.题目 2.题目接口 3.解题思路 3.最长增长子序列 1.题目 2.题目接口 3.解题思路 4.猜数字游戏II 1.题目 2.题目接口 3.解题思路 总结&a…...

ChatGPT帮助一名儿童确诊病因,之前17位医生无法确诊
9月13日,Today消息,一位名叫Alex的4岁儿童得了一种浑身疼痛的怪病,每天需要服用Motrin(美林)才能止痛。3年的时间,看了17名医生无法确诊病因。(新闻地址:https://www.today.com/heal…...

Laf 云开发平台及其实现原理
Laf 产品介绍 自我介绍 大家好,我是来自 Laf 团队的王子俊,很高兴今天能在这里给大家分享我们 Laf 云开发平台及其实现原理。本来想说一点什么天气之类的话作为开头,但主持人都说完啦,我就不多说了,还是直接开始今天…...

浅谈STL|STL函数对象篇
一.函数对象概念 概念: 重载函数调用操作符的类,其对象常称为函数对象 函数对象使用重载的()时,行为类似函数调用,也叫仿函数 本质: 函数对象(仿函数)是一个类,不是一个函数 特点 函数对象在使用时,可以像普通函数那…...
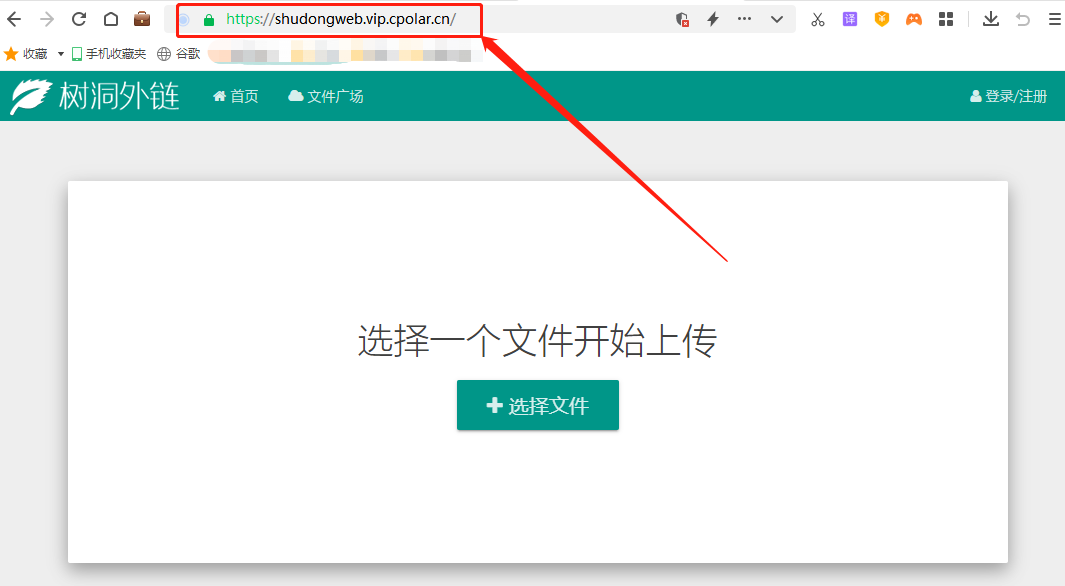
自建私人图床方案:使用Cpolar+树洞外链轻松部署超轻量级图床,实现高效图片存储
文章目录 1.前言2. 树洞外链网站搭建2.1. 树洞外链下载和安装2.2 树洞外链网页测试2.3 cpolar的安装和注册 3.本地网页发布3.1 Cpolar临时数据隧道3.2 Cpolar稳定隧道(云端设置)3.3 Cpolar稳定隧道(本地设置) 4.公网访问测试5.结语…...

从零基础到精通Flutter开发:一步步打造跨平台应用
💂 个人网站:【工具大全】【游戏大全】【神级源码资源网】🤟 前端学习课程:👉【28个案例趣学前端】【400个JS面试题】💅 寻找学习交流、摸鱼划水的小伙伴,请点击【摸鱼学习交流群】 导言 Flutter是一种流行…...

SpringBoot整合WebSocket【代码】
系列文章目录 一、SpringBoot连接MySQL数据库实例【tk.mybatis连接mysql数据库】 二、SpringBoot连接Redis与Redisson【代码】 三、SpringBoot整合WebSocket【代码】 四、SpringBoot整合ElasticEearch【代码示例】 文章目录 系列文章目录代码下载地址一、效果演示二、引入依赖…...
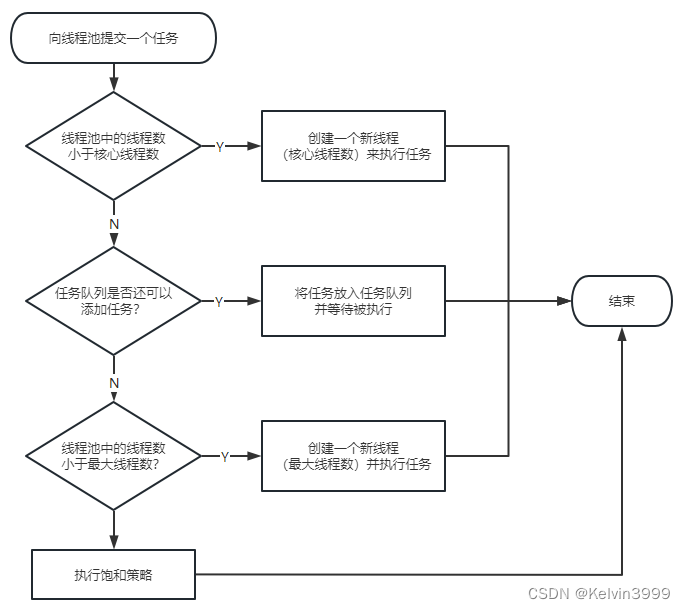
微服务 第一章 Java线程池技术应用
系列文章目录 第一章 Java线程池技术应用 文章目录 系列文章目录[TOC](文章目录) 前言1、Java创建线程方式回顾1.1、继承Thread类(只运行一次)1.1.1、改造成主线程常驻,每秒开启新线程运行1.1.2、匿名内部类1.1.3、缺点1.1.4、扩展知识:Java内部类1.1.4…...
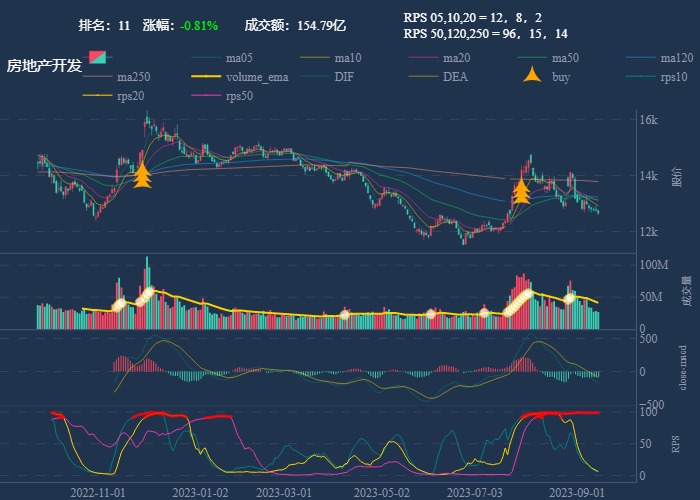
行业追踪,2023-09-14
自动复盘 2023-09-14 凡所有相,皆是虚妄。若见诸相非相,即见如来。 k 线图是最好的老师,每天持续发布板块的rps排名,追踪板块,板块来开仓,板块去清仓,丢弃自以为是的想法,板块去留让…...

传输层协议--UDP
引入 传输层负责数据能够从发送端传输到接收端。 端口号(Port) 端口号标识了一个主机上进行通信的一个进程。 两个问题: 1. 一个进程可以绑定多个端口号吗?--可以 2.一个端口号可以绑定多个进程吗?--不可以 我们…...
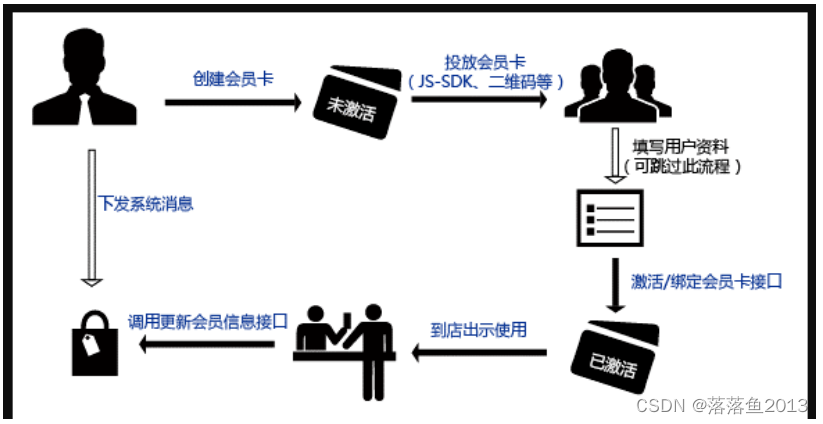
微信会员卡开发流程
功能需求: 通过微信第三方平台创建的模板小程序,想要实现用户在小程序支付一定金额后领取会员卡,领取会员卡后可给用户下发一定数量的优惠券,并且实现用户在小程序消费享受商品折扣。 开发流程: 一、了解微信的3个平…...

《算法竞赛·快冲300题》每日一题:“点灯游戏”
《算法竞赛快冲300题》将于2024年出版,是《算法竞赛》的辅助练习册。 所有题目放在自建的OJ New Online Judge。 用C/C、Java、Python三种语言给出代码,以中低档题为主,适合入门、进阶。 文章目录 题目描述题解C代码Java代码Python代码 “ 点…...
)
常见高级语言的输入与输出训练(一)
文章目录 题目概述1 输入描述: 输出描述: 输入 输出 示例C语言代码 题目概述2 题目描述 输入描述: 输出描述: 输入 输出 示例Java代码 前言 本文主要讲解两个算法题的代码实现 题目概述1 计算ab 打开以下链接可以查看正确的代码 数据范围:数据组数满…...

恭喜!龙蜥获得 2023 大学生操作系统设计赛二等奖及特殊贡献奖
经过多月的激烈角逐,2023 全国大学生系统能力大赛操作系统设计赛(以下简称“2023 大学生操作系统赛”) 圆满结束。经过 2023 大学生操作系统赛评审组和技术委员会的复核,面向全国公布了此次大赛的获奖名单。龙蜥社区不负众望&…...
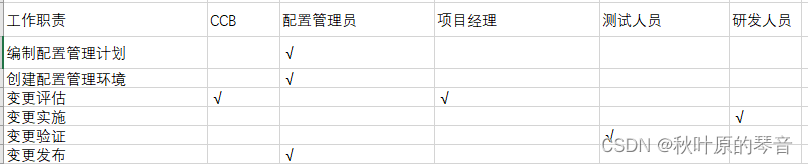
中项系统集成项目管理2023上半年真题及解析
中项系统集成项目管理2023上半年真题及解析 上午题1. 在 (1) 领域,我国还远未达到世界先进水平,需要发挥新型举国体制优势,集中政府和市场两方面的力量全力发展2. ChatGPT于 2022年 11 月 30 日发布,它是人工智能驱动的 (2) 工具3…...

实时显示当前文件夹下的文件大小,shell脚本实现
图片来源于网络,如果侵权请联系博主删除! 需求: 写一个shell终端命令,实时显示当前文件夹下的文件大小 实现: 您可以使用以下的Shell脚本命令来实时显示当前文件夹下的文件大小: while true; docleardu …...
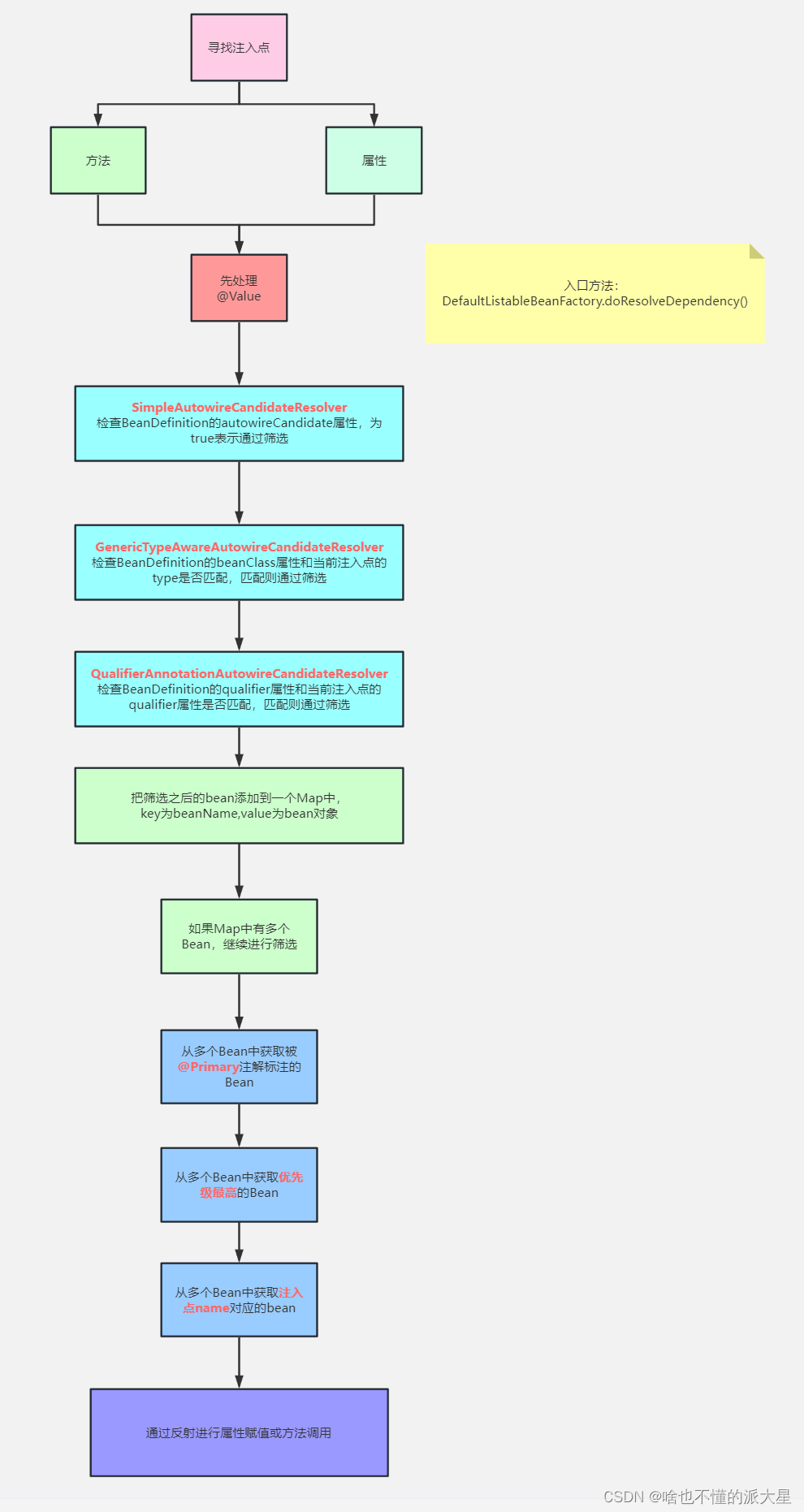
7、Spring之依赖注入源码解析(下)
resolveDependency()实现 该方法表示,传入一个依赖描述(DependencyDescriptor),该方法会根据该依赖描述从BeanFactory中找出对应的唯一的一个Bean对象。 @Nullable Object resolveDependency(DependencyDescriptor descriptor, @Nullable String requestingBeanName,@Null…...
图片码二次渲染绕过
目录 一、环境 1、代码 2、文件处理方式 3、图片码的制作 二、绕过图片重构 1、可行性分析 2、数据比对 3、完成绕过 一、环境 以upload-labs靶场第十七关为例 1、代码 源码为: <?php include ../config.php; include ../head.php; include ../menu.…...

点评项目核心内容
目录 拦截器设置 集群的session共享问题 基于redis实现共享session登录 创建bean对象技巧 什么是缓存 使用缓存来处理对象 使用String类型缓存来处理集合 缓存更新策略 主动更新策略 缓存穿透 空串""和null的区别 缓存null值解决穿透问题 缓存雪崩 缓存击穿…...

海外商城小程序为什么这么受欢迎?
随着全球化的进程海外商城小程序在近年来获得了广泛的关注和使用。海外商城小程序是一种基于互联网技术的应用程序,为用户提供了便捷的购物体验和跨境交易服务。本文将深入探讨海外商城小程序的受欢迎原因,从多个维度进行分析就其未来发展进行思考&#…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...