【C语言】每日一题(半月斩)——day2

目录
一.选择题
1、以下程序段的输出结果是( )
2、若有以下程序,则运行后的输出结果是( )
3、如下函数的 f(1) 的值为( )
4、下面3段程序代码的效果一样吗( )
5、对于下面的说法,正确的是( )
二,编程题
1.尼科彻斯定理
2.等差数列
一.选择题
1、以下程序段的输出结果是( )
int main()
{char s[] = "\\123456\123456\t";printf("%d\n", strlen(s));return 0;
}
A: 12 B:13 C: 16 D: 以上都不对
解析:
考察的是转义字符
\\ 表示字符'\',\123表示字符'{',\t表示制表符;
转义字符通常考察两种:
①\ddd ddd表示1~3个八进制
②\xhh hh表示1~2个十六进制
正确答案:A
2、若有以下程序,则运行后的输出结果是( )
#include <stdio.h>
#define N 2
#define M N + 1
#define NUM (M + 1) * M / 2
int main()
{printf("%d\n", NUM);return 0;
}
A: 4 B: 8 C: 9 D: 6
解析:
考察的是define宏定义
宏只是替换,替换后NUM的样子是(2+1+1)*2+1/2,计算得8 ;
#define是宏定义,只进行替换
正确答案:B
3、如下函数的 f(1) 的值为( )
int f(int n)
{static int i = 1;if (n >= 5)return n;n = n + i;i++;return f(n);
}A:5 B:6 C:7 D:8
解析:
考察的是函数递归static修饰的局部变量——称为静态局部变量
static实际修改了局部变量的存储类型,将原本应该存储在栈区的局部变量存储在静态区。静态区上数据存储的特点是,程序结束变量才被释放。我们常见的全局变量就是存储在静态区上。现在我们分析static修饰后作用域和生命周期的变化:
【作用域】:作用域不变,只是出作用域不被销毁
【生命周期】:生命周期变长,程序结束生命周期才结束正确答案:C

4、下面3段程序代码的效果一样吗( )
int b;
①const int* a = &b;
②int const* a = &b;
③int* const a = &b;A: (2)=(3) B: (1)=(2) C: 都不一样 D: 都一样
解析:
考察的是const;
将变量转成常量
但并不是真正的变成常量,只是语法形式变成常量;本质上还是变量,
counst 修饰的变量不能再被改变;
修饰指针有两种方法
counst int* p ;
int * counst p;
- const 放在的左边
限制的指针指向的内容,也就是说: 不能通过指针来修改指针指向的内容
但是指针变量是可以修改的,也就是指针指向其他变量的
- const 放在的右边
限制的是指针变量本身,指针变量不能再指向其他对象
但是可以通过指针变量来修改指向的内容
正确答案:B
5、对于下面的说法,正确的是( )
A: 对于 struct X{short s;int i;char c;},sizeof(X)等于sizeof(s) + sizeof(i) + sizeof(c)
B: 对于某个double变量 a,可以使用 a == 0.0 来判断其是否为零
C: 初始化方式 char a[14] = "Hello, world!"; 和char a[14]; a = "Hello, world!";的效果相同
D: 以上说法都不对
解析:
考察的是结构体和sizeof;
A.没有考虑内存对齐
B.考察浮点型的比较,由于浮点型存在误差,不能直接判断两个数是否相等,通常采用比较两个数差的绝对值是否小于一个很小的数,作为误差
C.第二种的a代表首元素的地址,地址是常量不可以改变
正确答案:D
二,编程题
1.尼科彻斯定理
验证尼科彻斯定理,即:任何一个整数m的立方都可以写成m个连续奇数之和。
例如:
1^3=1
2^3=3+5
3^3=7+9+11
4^3=13+15+17+19
输入一个正整数m(m≤100),将m的立方写成m个连续奇数之和的形式输出。
数据范围:1≤m≤100
尼科彻斯定理——牛客网
#include<math.h>
int main()
{int m = 0;scanf("%d", &m);//获得m的三次幂的数int ret = pow(m, 3);printf("m的立方数:%d\n", ret);//如果m是1if (m == 1){printf("%d", m);}//找到首个元素int num = m * m - m + 1;//进行循环找到后面m个数字for (int i = 0; i < m; i++){//打印首个数字if (i == 0){printf("%d ", num);}//打印后面的else {printf("+ %d ", num);}num += 2;}return 0;
}通过示例发现,我们只要找到相加数字串的首个数字就可以通过+2的方式找到后面m-1个;
4^3=13+15+17+19;
首数字13是4*4-4+1得到的数字,然后就是通过循环找到后面几个数字;
2.等差数列
等差数列 2,5,8,11,14。。。。
(从 2 开始的 3 为公差的等差数列)
输出求等差数列前n项和
数据范围:1≤n≤1000
输入描述:
输入一个正整数n。
输出描述:
输出一个相加后的整数。
等差数列———牛客网
int main()
{int n = 0;int arr[1000];scanf("%d", &n);//将等差数列存入数组for (int i = 0; i < 1000; i++){arr[i] = 3 * (i + 1) - 1;}//将等差数累加int sum = 0;for (int j = 0; j < n; j++){sum = sum + arr[j]; }printf("%d", sum);return 0;
}

相关文章:

【C语言】每日一题(半月斩)——day2
目录 一.选择题 1、以下程序段的输出结果是( ) 2、若有以下程序,则运行后的输出结果是( ) 3、如下函数的 f(1) 的值为( ) 4、下面3段程序代码的效果一样吗( ) 5、对于下面的说法,正确的是…...

电脑如何查看代理服务器IP?
许多人在使用互联网时可能会遇到需要使用代理服务器的情况。但是,你知道如何在电脑上查看代理服务器IP吗?本文将为您分享简单易懂的方法,帮助您轻松了解代理设置的秘密! 代理服务器在网络世界中担任着重要的角色,它可…...

【C++11】{}初始化、std::initializer_list、decltype、STL新增容器
文章目录 1. C11简介2. 统一的列表初始化2.1 {}初始化2.2 std::initializer_list 3. 声明3.1 auto3.2 decltype 4. nullptr5. 范围for循环6. 智能指针7. C11STL中的一些变化8. 演示代码 1. C11简介 在2003年C标准委员会曾经提交了一份技术勘误表(简称TC1…...

【FPGA项目】进阶版沙盘演练——报文收发(报文处理、CDC、CRC)
前言 书接上文【FPGA项目】沙盘演练——基础版报文收发_子墨祭的博客-CSDN博客,前面我们做了基础版的报文收发,相信对逻辑设计有了一定的认知,在此基础上,继续完善一个实际报文收发可能会遇到的一些处理: 报文处理握手…...

【程序员装机】自定义Edge浏览器用户目录
文章目录 前言修改Edge用户目录的批处理脚本上述批处理脚本的功能包括 总结 前言 本文将介绍Edge浏览器用户目录的批处理脚本方式修改,以自定义Edge浏览器的磁盘缓存目录和用户数据目录。 修改Edge用户目录的批处理脚本 以下是一个用于修改Edge浏览器用户目录的批…...
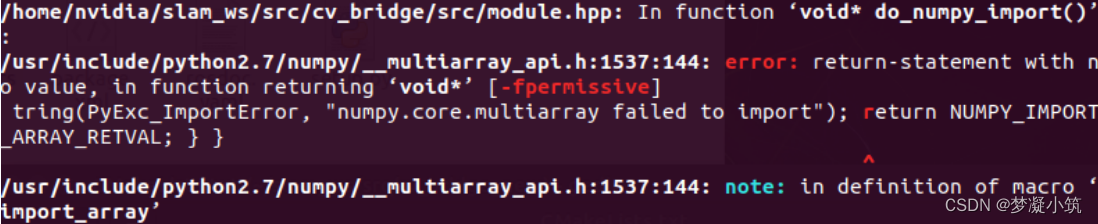
ubuntu18、20 cv_bridge 与自带opencv版本冲突问题
背景: nvidia tx2、xvaier 装机自带 ubuntu18 opencv4 后来我们会安装melodic的ros,ros中的cv_bridge 默认cv版本是3.2.0 编译带cv_bridge的代码时,会报错会崩溃,因为版本冲突了 为了解决该问题, 行之有效的一种…...

贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析免疫球蛋白、前列腺癌数据...
原文链接:http://tecdat.cn/?p22702 贝叶斯回归分位数在最近的文献中受到广泛关注,本文实现了贝叶斯系数估计和回归分位数(RQ)中的变量选择,带有lasso和自适应lasso惩罚的贝叶斯(点击文末“阅读原文”获取…...
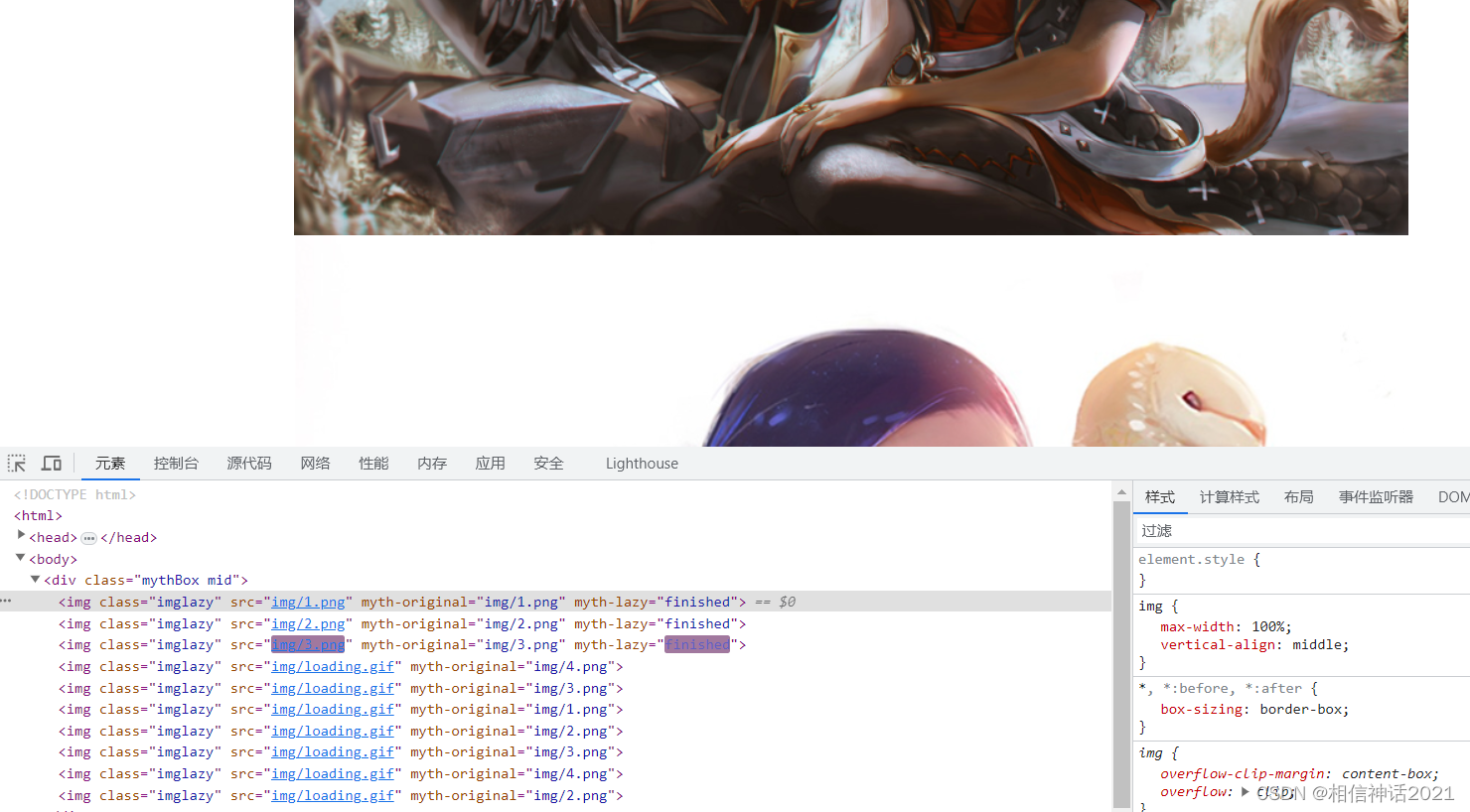
css自学框架之图片懒加载
首先解释一下什么叫图片懒加载。图片懒加载是一种在页面加载时,延迟加载图片资源的技术,也就是说图片资源在需要的时候才会加载,就是在屏幕显示范围内加载图片,屏幕显示范围外图片不加载。 一、关键函数 用到的关键函数…...

RoutingKafkaTemplate,DefaultKafkaProducerFactory和 ReplyingKafkaTemplate
一、RoutingKafkaTemplate 1.1、RoutingKafkaTemplate 能做什么 RoutingKafkaTemplate可以根据目标topic名称在运行时选择生产者。 RoutingKafkaTemplate 不支持事务、execute、flush或metrics操作,因为这些操作的主题未知。 1.2、使用前提 RoutingKafkaTemplate 和 KafkaT…...

Flutter动态化开发之Fair实战
一、背景 目前移动端应用的版本更新, 最常见的方式是定期发版,无论是安卓还是iOS,都需要提交新的安装包到应用市场进行审核。审核通过后,用户在应用市场进行App的下载更新。而动态化, 就是不依赖更新程序安装包, 就能动态实时更新页面的技术。 相比动态化技术,定期发版…...

Stream流编程
流格式 Stream<T> filter(Predicate<? super T> predicate);-----> 参数:public interface Predicate<T> (函数式接口)----> 抽象方法:boolean test(T t);-----> 参数:public interface Consumer<T> (函…...
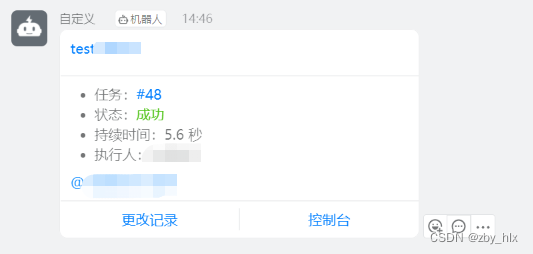
jenkins自动化脚本集成时钉钉消息未发送
在进行jenkins自动化脚本集成时,需要配置钉钉发送消息。钉钉的配置正确,测试钉钉消息发送成功,但是当构建项目时,却没有收到钉钉消息,报错如下: [钉钉插件]发送消息时报错: java.lang.NullPointerExceptio…...

java面试题第七天
一、java面试题第七天 1.方法重载和重写的区别? 方法重载:在同一个类中,不同的方法拥有同样的方法名,不一样的参数列表,这就叫做方法重载 **方法的重写:**描述的是父类和子类之间的。当父类的功能无法满…...
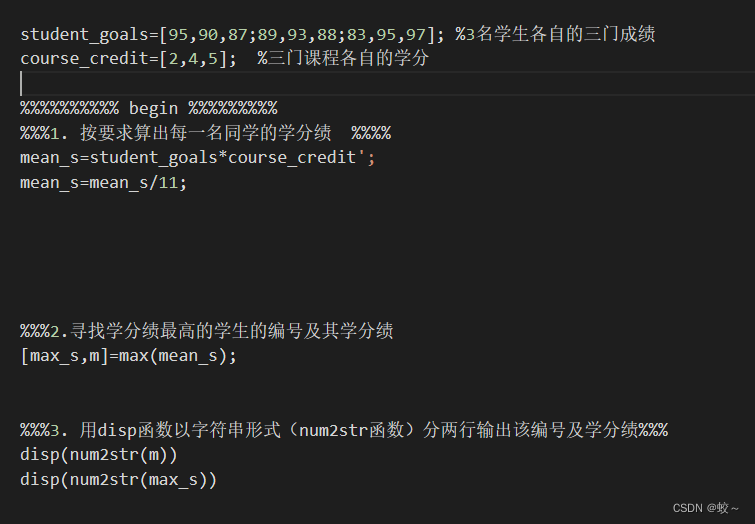
MATLAB入门-矩阵的运算
MATLAB入门-矩阵的运算 本篇文章为学习笔记,课程链接为:头歌 相关知识 常见的矩阵运算有算术运算、关系运算和逻辑运算。MATLAB中的所有变量都是以矩阵的形式存储的,单个变量就相当于一个1*1的矩阵。 算术运算 下面展示的是常见的矩阵之…...

[X3m]ros交叉编译
ros需要安装以下包 PYTHON_PACKAGE_LIST"lark lark-parser netifaces pyyaml ifcfg pyunicodedata " TogetheROS.Bot | TogetheROS.Bot用户手册 编译tros.b 1 使用docker文件 该部分操作均在开发机的docker内完成。 ## 创建目录 cd /mnt/data/kairui.wang/…...
【漏洞库】Fastjson_1.2.47_rce
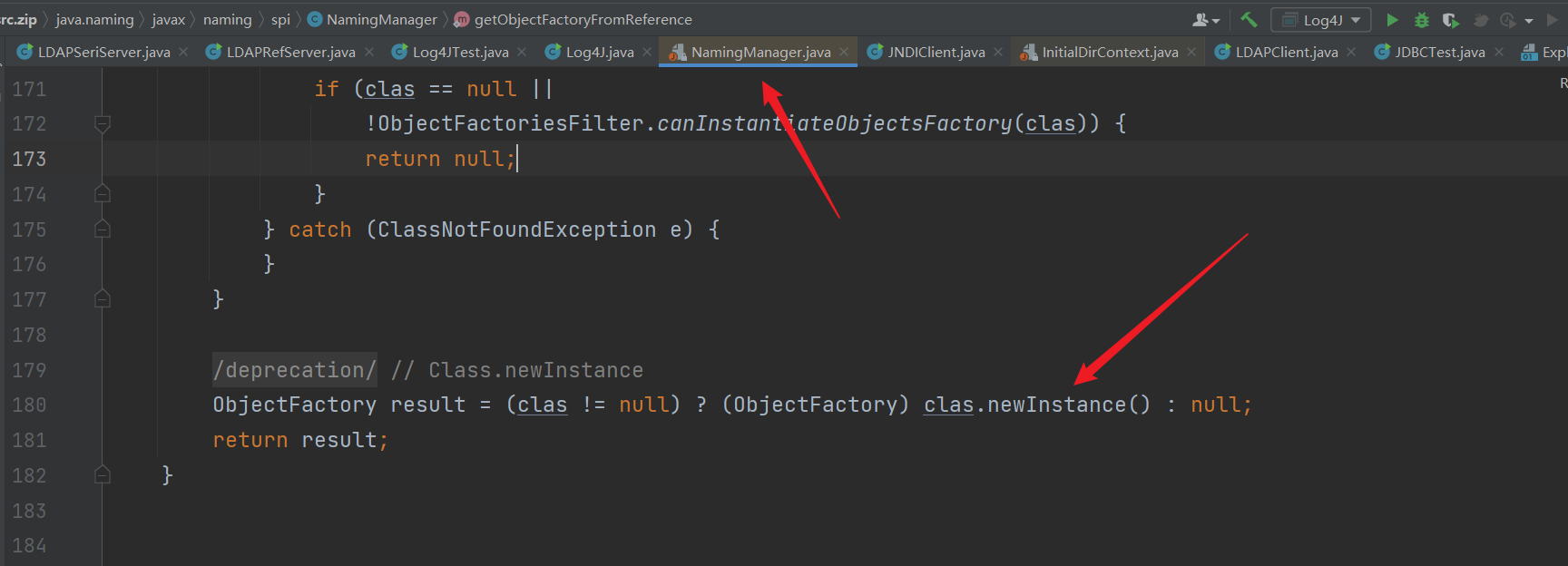
文章目录 漏洞描述漏洞编号漏洞评级影响版本漏洞复现- 利用工具- 漏洞环境- 漏洞扫描- 漏洞验证- 深度利用- GetShell- EXP 编写 漏洞挖掘- 寻找入口点- 指纹信息 修复建议- 漏洞修复 漏洞原理 漏洞描述 Fastjson是阿里巴巴公司开源的一款json解析器,其性能优越&am…...
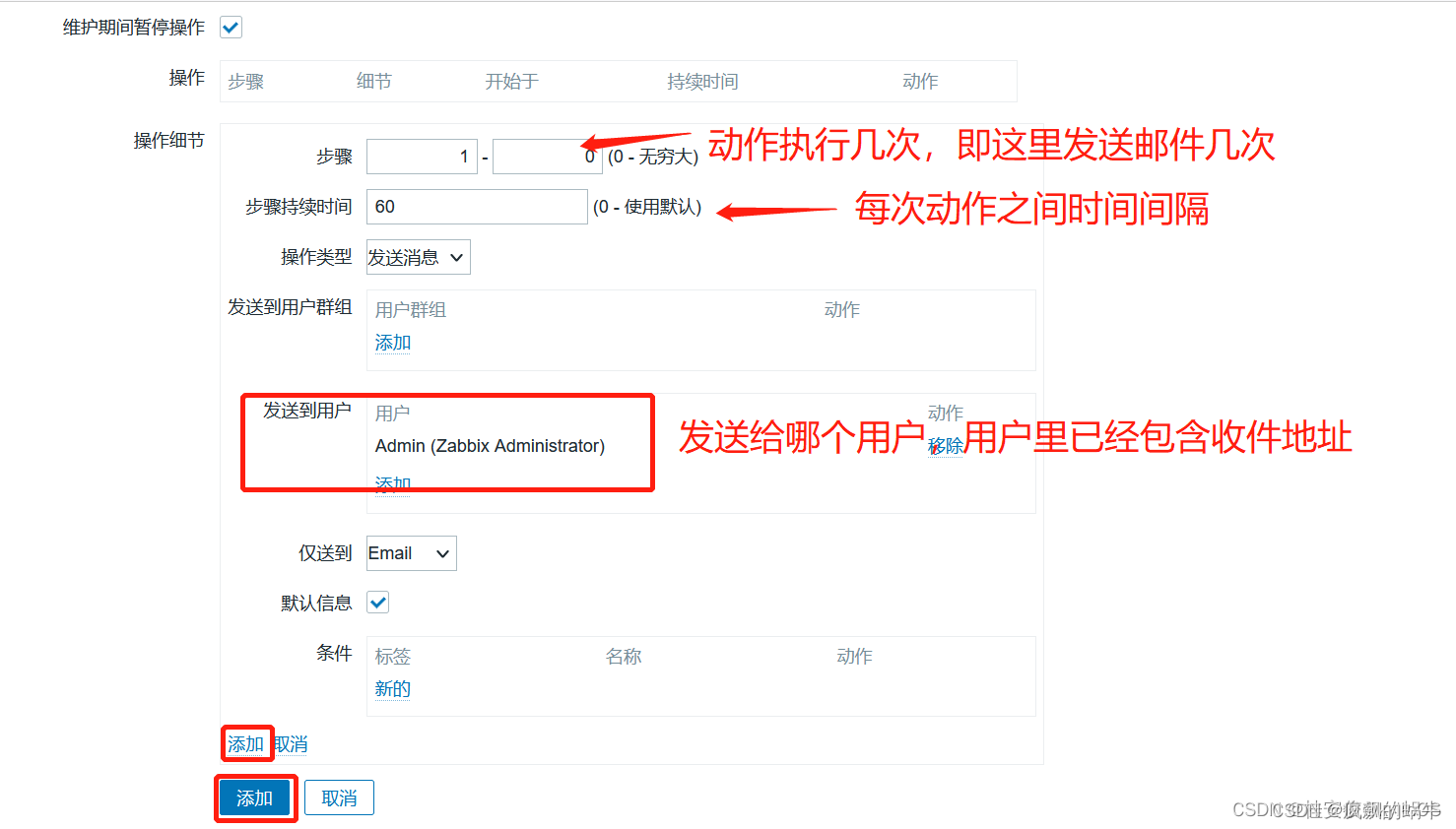
zabbix 钉钉微信企微告警(动作操作消息内容模板)
一、环境配置 1、配置zabbix服务端 2、配置监控主机&监控项&监控模板 zabbix配置安装_this page is used to test the proper operation of _疯飙的蜗牛的博客-CSDN博客 二、触发器 触发器的本质就是一个条件判断,对于不同的监控数据来说,我…...

阿里云国际站云服务器数据备份方法有哪些?
阿里云国际站云服务器是一种根据云计算技术的虚拟服务器,它能够经过互联网提供计算资源和服务。在运用云服务器的过程中,数据备份是非常重要的一个环节。本文将介绍云服务器数据备份的办法,包含手动备份、主动备份和数据同步。 一、手动备份 …...

游戏笔记本电脑可以进行 3D 建模和渲染吗?有哪些优势与缺点?
3D 建模和渲染是创建令人惊叹的数字艺术、动画和游戏体验的最流行和最广泛使用的工具之一。随着技术的进步,对运行这些模型的强大计算机的需求呈指数级增长。对于那些寻求强大机器来处理 3D 建模任务的人来说,游戏笔记本电脑已成为一个可行的选择。 游戏…...

【AI】推理系统和推理引擎的整体架构
本文主要是对 B 站 Up 主 ZOMI酱 推理系统系列视频 的理解,可以认为是重点笔记。 一、深度学习模型的全生命周期 相信很多人和我一样,刚看到深度学习模型中的推理系统或推理引擎时是一头雾水,因为学习 DL 时通常关注于模型的设计和训练。下图…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...
