当前位置： 首页 > news >正文

【Spring Boot自动装配】

news 2026/3/29 9:33:07

Spring Boot启动的时候会通过@EnableAutoConfiguration注解找到META-INF/spring.factories配置文件中的所有自动配置类，并对其进行加载，而这些自动配置类都是以AutoConfiguration结尾来命名的，它实际上就是一个JavaConfig形式的Spring容器配置类，它能通过以Properties结尾命名的类中取得在全局配置文件中配置的属性如：server.port，而XxxxProperties类是通过@ConfigurationProperties注解与全局配置文件中对应的属性进行绑定的。
启动类的@SpringBootApplication注解由@SpringBootConfiguration，@EnableAutoConfiguration，@ComponentScan三个注解组成，三个注解共同完成自动装配；

  • @SpringBootConfiguration 注解标记启动类为配置类
  • @ComponentScan 注解实现启动时扫描启动类所在的包以及子包下所有标记为bean的类由IOC容器注册为bean
  • @EnableAutoConfiguration通过 @Import 注解导入 AutoConfigurationImportSelector类，然后通过AutoConfigurationImportSelector 类的 selectImports 方法去读取需要被自动装配的组件依赖下的spring.factories文件配置的组件的类全名，并按照一定的规则过滤掉不符合要求的组件的类全名，将剩余读取到的各个组件的类全名集合返回给IOC容器并将这些组件注册为bean。

相关文章：

【Spring Boot自动装配】

Spring Boot启动的时候会通过EnableAutoConfiguration注解找到META-INF/spring.factories配置文件中的所有自动配置类，并对其进行加载，而这些自动配置类都是以AutoConfiguration结尾来命名的，它实际上就是一个JavaConfig形式的Spring容器配置…...

编程日记 2023/9/15 6:57:18

windows彻底卸载unity

1.控制面板卸载 双击打开桌面的控制面板，选择卸载程序，选中Unity和UnityHub右击卸载。 2.清除unity的注册表 在运行中输入“regedit”双击打开注册表界面 删除 HKEY_CURRENT_USER\Software\Unity 下所有项 删除 HKEY_CURRENT_USER\Software\Unity Tec…...

编程日记 2023/9/15 6:53:14

Java项目-苍穹外卖-Day10-SpirngTask及WebSocket

文章目录 前言SpringTask介绍SpringTask_corn表达式Spring_Task入门案例 订单状态定时处理需求分析代码开发功能测试 WebScoket介绍入门案例 来单提醒需求分析代码开发功能测试 客户催单代码开发功能测试 前言 本章实现的业务功能 超时未支付订单自动取消，配送中订…...

编程日记 2023/9/15 6:51:12

Spring IOC 容器：掌握 Spring 的核心技术

Spring 是一个非常流行和强大的 Java 开发框架，它可以帮助我们简化和优化 Java 项目的开发过程。Spring 的核心技术之一就是 IOC（Inversion of Control，控制反转），它可以实现对象之间的解耦，让对象的创建和…...

编程日记 2023/9/15 6:50:11

python实现批量从excel列表显示图片网址中下载图片

遇到一个需求：给了一个excel表，里面有很多网址图片，要把图片下载到本地。手动操作的话就是在浏览器里输入网址，再图片另存为保存。这篇文章介绍一下使用python代码批量实现 第一步操作就是实现从网上下图片，这个用到了…...

编程日记 2023/9/15 6:49:10

java 单元测试Junit

所谓单元测试，就是针对最小的功能单元，编写测试代码对其进行正确性测试。为了测试更加方便，有一些第三方的公司或者组织提供了很好用的测试框架，给开发者使用。这里介绍一种Junit测试框架。Junit是第三方公司开源出来的&#xff0…...

编程日记 2023/9/15 6:48:09

Java中Timer和TimerTask的使用

这两个类使用起来非常方便，可以完成我们对定时器的绝大多数需求 Timer类是用来执行任务的类，它接受一个TimerTask做参数 Timer有两种执行任务的模式,最常用的是schedule,它可以以两种方式执行任务:1:在某个时间(Data)，2:在某个固定的时间之后…...

编程日记 2023/9/15 6:45:07

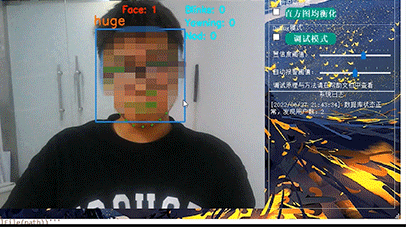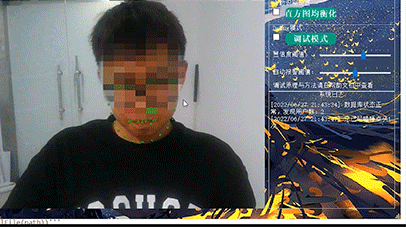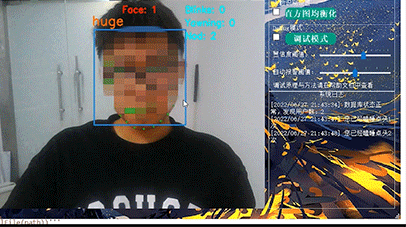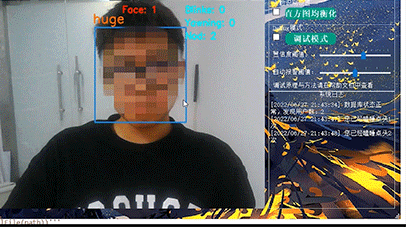
计算机竞赛 机器视觉 opencv 深度学习 驾驶人脸疲劳检测系统 -python

文章目录 0 前言1 课题背景2 Dlib人脸识别2.1 简介2.2 Dlib优点2.3 相关代码2.4 人脸数据库2.5 人脸录入加识别效果 3 疲劳检测算法3.1 眼睛检测算法3.2 打哈欠检测算法3.3 点头检测算法 4 PyQt54.1 简介4.2相关界面代码 5 最后 0 前言 🔥 优质竞赛项目系列&#x…...

编程日记 2023/9/15 6:44:06

DFS寻找从s到t的所有路径

问题描述&#xff1a; 输入一个有向图&#xff0c;输出从s到t的所有路径的结点 输入&#xff1a; 3 3 0 1 1 2 0 2输出&#xff1a; 0 1 2 0 2 代码&#xff1a; #include<bits/stdc.h> using namespace std;const int N 103; vector<int>e[N];//用行为N的…...

编程日记 2023/9/15 6:38:02

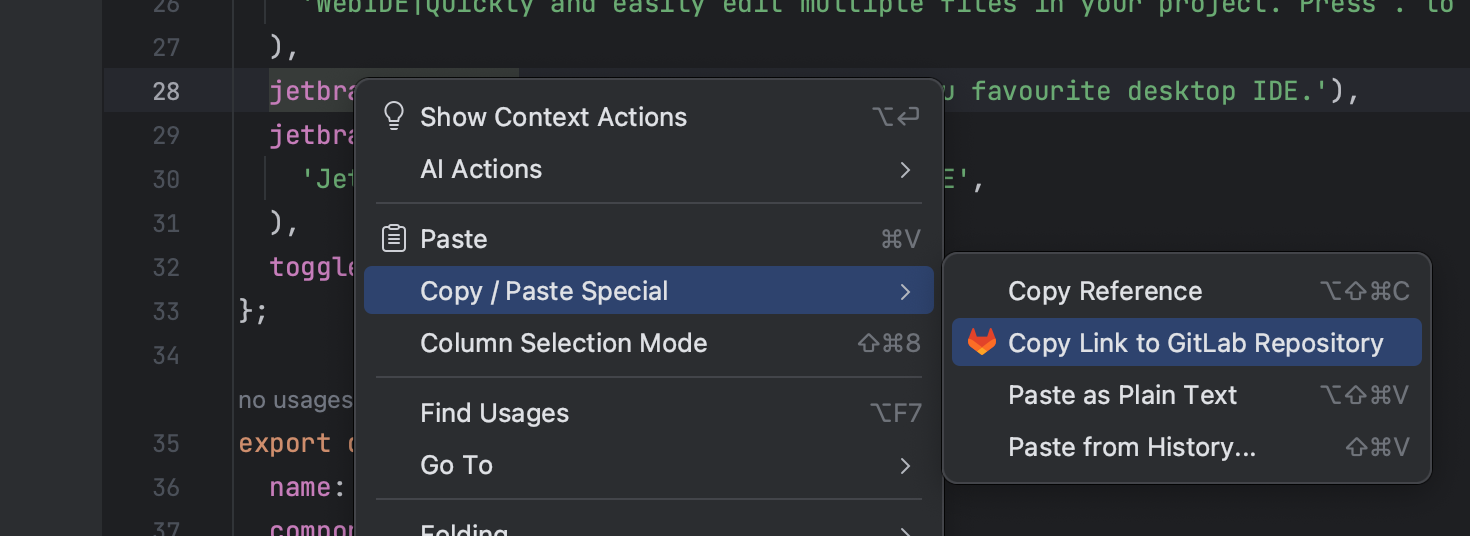
分享！JetBrains IDE中的GitLab支持

GitLab是流行的基于git的软件开发和部署平台之一&#xff0c;虽然很长一段时间以来&#xff0c;所有基本git操作都已经可以通过GitLab实现&#xff0c;但GitLab集成仍是JetBrains社区的一大最热门请求。为此&#xff0c;JetBrains团队今年与GitLab联手提供了这种类型的集成。 …...

编程日记 2023/9/15 6:37:01

jq弹窗拖动改变宽高

预览效果 <div classtishiMask><div class"tishiEm"><div id"coor"></div><div class"topNew ismove"><span class"ismove">提示</span><p onclick"closeTishi()"></p&…...

编程日记 2023/9/15 6:35:59

时间不确定度在分布式系统中的说明

On the one hand 时间不确定度问题和影响在分布式系统中 说明 时钟不确定度&#xff08;Clock Uncertainty&#xff09;是指在分布式系统中&#xff0c;由于网络延迟、时钟漂移等因素导致系统中各个节点时钟的不同步现象。这种不同步可能会影响到分布式系统的一致性和正确性…...

编程日记 2023/9/15 6:34:58

VMware vCenter 从6.7跨版本升级至7.0U3N

本文尝试使用 vCenter Server Appliance 管理界面 (VAMI) 进行对vCenter Server Appliance7应用进行小版本升级&#xff0c;从6.7.0.47000升级到7.0.3.01600&#xff08;7.0U3N&#xff09;。 一、升级前的准备工作 1、检查当前运行环境&#xff08;当前为6.7.0.47000&#x…...

编程日记 2023/9/15 6:33:58

大麦订单生成器最新版 大麦订单一键生成截图

1.可以一键添加&#xff0c;生成的假订单没有水印&#xff0c;界面也很真实。 2.在软件中输入生成的信息&#xff0c;这是产品信息&#xff0c;选择生成的产品图像&#xff0c;最后生成它。 后台一键生成&#xff0c;独立后台管理 教程&#xff1a;解压源码&#xff0c;修改数…...

编程日记 2023/9/15 6:32:57

如何对Map集合的key进行大小写转换？

工具类&#xff1a; ToUpperCaseKeyMapUtil.java public class ToUpperCaseKeyMapUtil {//对单一的mappublic static <T> Map<String, T> toUpperCaseKeyMap(Map<String, T> map) {if (map ! null) {List<String> mapKeyList new ArrayList<>…...

编程日记 2023/9/15 6:31:56

将函数实现放到CPP报“无法解析的外部符号...”，系VS Bug

发现一个现象&#xff0c;就是项目中有一个类&#xff0c;如果将函数实现全部放到头文件中&#xff0c;编译不报错&#xff0c;如果将函数实现放到CPP中则始终提示“无法解析的外部符号...”&#xff0c;考虑到放到头文件中能正常编译运行&#xff0c;显然这里不符合“无法解析…...

编程日记 2023/9/15 6:29:54

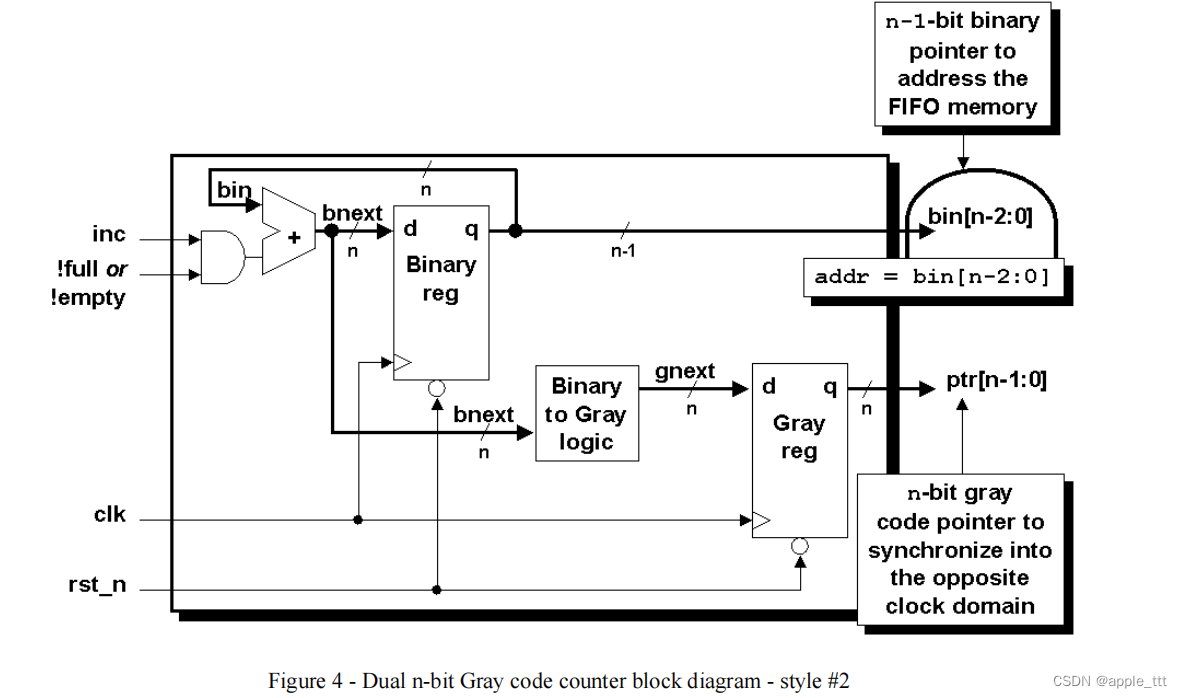
异步FIFO设计的仿真与综合技术（3）

概述 本文主体翻译自C. E. Cummings and S. Design, “Simulation and Synthesis Techniques for Asynchronous FIFO Design 一文&#xff0c;添加了笔者的个人理解与注释&#xff0c;文中蓝色部分为笔者注或意译。前文链接&#xff1a; 异步FIFO设计的仿真与综合技术&#xf…...

编程日记 2023/9/15 6:28:53

什么是区块链，解释区块链的原理和应用场景

1、什么是区块链&#xff0c;解释区块链的原理和应用场景。 区块链是一种分布式数据库&#xff0c;它由一系列按照时间顺序排列的数据块组成&#xff0c;并采用密码学方式保证不可篡改和不可伪造。区块链技术最初起源于比特币&#xff0c;作为比特币的底层技术&#xff0c;用于…...

编程日记 2023/9/15 6:27:52

使用bert进行文本二分类

构建BERT&#xff08;Bidirectional Encoder Representations from Transformers&#xff09;的训练网络可以使用PyTorch来实现。下面是一个简单的示例代码&#xff1a; import torch import torch.nn as nn from transformers import BertModel, BertTokenizer# Load BERT to…...

编程日记 2023/9/15 6:26:51

用Windows Installer CleanUp Utility 在windows server上面将软件卸载干净，比如SQLSERVER

这里写自定义目录标题 下载文件&#xff1a;Windows Installer CleanUp Utility。 通过以上工具可以将一个应用程序卸载干净。...

编程日记 2023/9/15 6:25:50

Anything-v5模型微调启示：Pixel Fashion Atelier对动漫风格像素化表达的重构

Anything-v5模型微调启示&#xff1a;Pixel Fashion Atelier对动漫风格像素化表达的重构 1. 项目背景与设计理念 Pixel Fashion Atelier是一个创新的图像生成工作站&#xff0c;它巧妙融合了Stable Diffusion的强大生成能力与Anything-v5模型对动漫风格的精准把控。这个项目最…...

编程新知 2026/3/29 9:22:02

终极指南：如何快速配置HsMod插件提升炉石传说游戏体验

终极指南&#xff1a;如何快速配置HsMod插件提升炉石传说游戏体验 【免费下载链接】HsMod Hearthstone Modify Based on BepInEx 项目地址: https://gitcode.com/GitHub_Trending/hs/HsMod HsMod是一个基于BepInEx框架开发的炉石传说游戏插件&#xff0c;专为希望提升游…...

编程新知 2026/3/29 7:19:23

广汽埃安品牌车型AION UT在奥地利麦格纳工厂正式量产启动并成功下线 | 美通社头条

、美通社消息&#xff1a;3月18日&#xff0c;广汽欧洲业务发展迎来重要里程碑——旗下埃安品牌车型AION UT在奥地利麦格纳(Magna)工厂正式实现量产启动(SOP)并成功下线&#xff0c;标志着广汽在欧洲本地化战略迈入实质性推进阶段。AION UT是广汽欧洲本地化战略的重要核心车型&…...

编程新知 2026/3/29 6:08:22

从nvidia-smi到npu-smi：给CUDA开发者的华为昇腾NPU监控指南

从nvidia-smi到npu-smi&#xff1a;CUDA开发者快速掌握昇腾NPU监控的实战手册 当你的技术栈从英伟达GPU扩展到华为昇腾NPU时&#xff0c;监控工具的使用体验就像从自动挡切换到手动挡——虽然最终目的地相同&#xff0c;但操作逻辑需要重新适应。作为曾经每天与nvidia-smi打交道…...

编程新知 2026/3/29 5:48:06

AI原生应用开发：边缘设备上的实时目标检测实现

AI原生应用开发&#xff1a;边缘设备上的实时目标检测实现关键词&#xff1a;AI原生应用开发、边缘设备、实时目标检测、计算机视觉、深度学习摘要&#xff1a;本文聚焦于AI原生应用开发中在边缘设备上实现实时目标检测这一重要课题。详细介绍了边缘设备实时目标检测的核心概念…...

编程新知 2026/3/29 4:35:20

HRN模型与PID控制结合：实时面部动画调节系统

HRN模型与PID控制结合&#xff1a;实时面部动画调节系统 1. 引言 想象一下&#xff0c;你正在制作一部动画电影&#xff0c;主角的面部表情需要精确到每一帧的微妙变化。传统的手工调整方式耗时耗力&#xff0c;而自动生成的表情又往往缺乏自然流畅的过渡。这就是为什么我们需…...

编程新知 2026/3/29 3:30:40

BongoCat：让桌面交互充满生命力的开源伴侣

BongoCat&#xff1a;让桌面交互充满生命力的开源伴侣 【免费下载链接】BongoCat 让呆萌可爱的 Bongo Cat 陪伴你的键盘敲击与鼠标操作&#xff0c;每一次输入都充满趣味与活力&#xff01; 项目地址: https://gitcode.com/gh_mirrors/bong/BongoCat 在数字化工作与娱乐…...

编程新知 2026/3/29 3:16:34

LVGL显存、FreeRTOS堆栈、全局变量：在128KB RAM的STM32F407上如何做内存预算与平衡？

LVGL显存、FreeRTOS堆栈与全局变量的内存博弈&#xff1a;STM32F407的128KB RAM精算指南 当一块STM32F407芯片的128KB RAM需要同时供养LVGL的华丽界面、FreeRTOS的多任务调度以及应用层的全局变量时&#xff0c;开发者面临的挑战不亚于一位财务总监在有限预算下平衡多个部门的开…...

编程新知 2026/3/29 2:54:17

springboot-vue+nodejs大学生作业管理系统的设计与实现

目录技术栈选择系统模块划分开发阶段规划部署方案设计进度与风险管理项目技术支持源码获取详细视频演示 &#xff1a;文章底部获取博主联系方式&#xff01;同行可合作技术栈选择 后端采用Spring Boot框架&#xff0c;提供RESTful API接口&#xff0c;处理业务逻辑和数据持久化…...

编程新知 2026/3/29 2:54:17

AI原生应用中的个性化推荐算法实战解析

AI原生应用中的个性化推荐算法实战解析 关键词&#xff1a;AI原生应用、个性化推荐、协同过滤、深度学习推荐模型、冷启动问题 摘要&#xff1a;在AI技术深度渗透的今天&#xff0c;“AI原生应用”&#xff08;AI Native Apps&#xff09;已从概念走向落地。这类应用的核心特征…...

编程新知 2026/3/29 0:37:10