当前位置： 首页 > news >正文

uniapp抽取组件绑定事件中箭头函数含花括号无法解析

news 2026/2/8 1:25:00

版本:  "@dcloudio/uni-ui": "^1.4.27", "vue": ">= 2.6.14 < 2.7"... 

箭头函数后含有花括号的时候, getData就拿不到val参数 , 解决办法就是去除花括号

// 错误代码:
<SearchComp @change="(val) => { getData({ val }) } "></SearchComp>// 正确代码
<SearchComp @change="(val) => getData({ val }) "></SearchComp>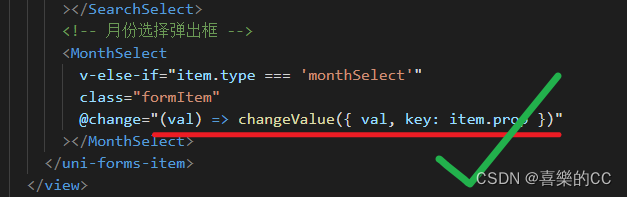

相关文章：

uniapp抽取组件绑定事件中箭头函数含花括号无法解析

版本: "dcloudio/uni-ui": "^1.4.27", "vue": "> 2.6.14 < 2.7"... 箭头函数后含有花括号的时候, getData就拿不到val参数 , 解决办法就是去除花括号 // 错误代码: <SearchComp change"(val) > { getData({ val …...

编程日记 2023/9/15 9:24:44

猫头虎博主第四期赠书活动：《精通Go语言：(第2版) 》

&#x1f337;&#x1f341; 博主猫头虎&#xff08;&#x1f405;&#x1f43e;&#xff09;带您 Go to New World✨&#x1f341; &#x1f984; 博客首页——&#x1f405;&#x1f43e;猫头虎的博客&#x1f390; &#x1f433; 《面试题大全专栏》 &#x1f995; 文章图文…...

编程日记 2023/9/15 9:20:39

【学习总结】EasyExcel合并同列不同行，表格数据相同的行

实体类 Data HeadRowHeight(50) ContentStyle(horizontalAlignment HorizontalAlignmentEnum.CENTER, verticalAlignment VerticalAlignmentEnum.CENTER, wrapped BooleanEnum.TRUE) public class CriterionDataExportDTO {ColumnWidth(15)ExcelProperty(value "所属…...

编程日记 2023/9/15 9:19:38

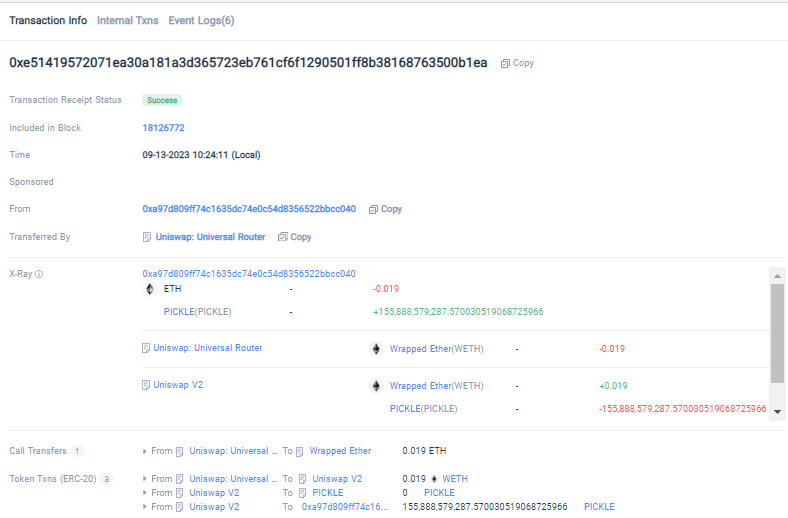
Tokenview X-ray功能：深入探索EVM系列浏览器的全新视角

Tokenview作为一家领先的多链区块浏览器&#xff0c;为了进一步优化区块链用户的使用体验&#xff0c;我们推出了X-ray&#xff08;余额透视&#xff09;功能。该功能将帮助您深入了解EVM系列浏览器上每个地址的交易过程&#xff0c;以一种直观、简洁的方式呈现地址的进出账情况…...

编程日记 2023/9/15 9:17:37

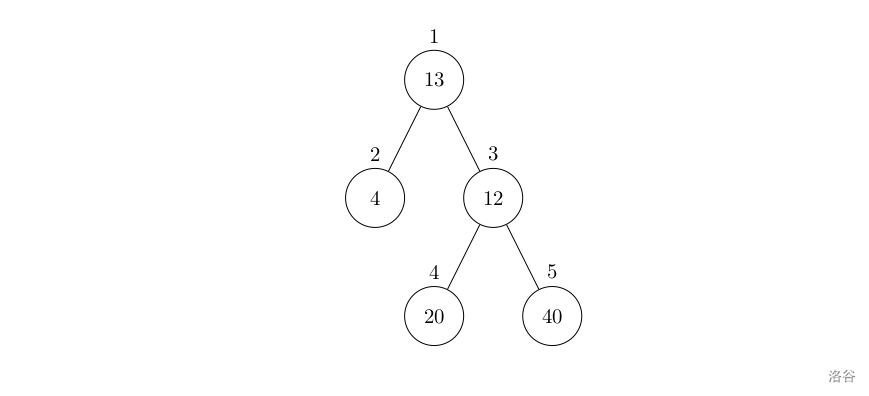
【洛谷 P1364】医院设置 题解（图论+深度优先搜索）

医院设置 题目描述 设有一棵二叉树&#xff0c;如图&#xff1a; 其中&#xff0c;圈中的数字表示结点中居民的人口。圈边上数字表示结点编号&#xff0c;现在要求在某个结点上建立一个医院&#xff0c;使所有居民所走的路程之和为最小&#xff0c;同时约定&#xff0c;相邻接…...

编程日记 2023/9/15 9:15:35

【Java基础】- RMI原理和使用详解

【Java基础】- RMI原理和使用详解 文章目录 【Java基础】- RMI原理和使用详解一、什么RMI二、RMI原理2.1 工作原理图2.2 工作原理 三、RMI远程调用步骤3.1 RMI远程调用运行流程图3.2 RMI 远程调用步骤 四、JAVA RMI简单实现4.1 如何实现一个RMI程序4.2 JAVA实现RMI程序 一、什么…...

编程日记 2023/9/15 9:10:30

无水印免费4K视频素材网站 可商用-Free Stock Video

Free Stock Video是一个在线无水印免费4K视频素材网站&#xff0c;提供各种类型的4k、1080p的视频素材共免费下载&#xff0c;包括美食、水、自然、冬季、无人机、云朵、慢动作、夕阳、动态背景、缩时摄影、旅游和烟火&#xff0c;也可通过关键词搜索方式找到相关视频素材内容&…...

编程日记 2023/9/15 9:09:29

kubesphere中间件部署

微服务部署前中间件部署 一、MySQL部署 1.1 使用Docker实现MySQL主从复制 docker run -p 3307:3306 --name mysql-master \ -v /mydata/mysql/master/log:/var/log/mysql \ -v /mydata/mysql/master/data:/var/lib/mysql \ -v /mydata/mysql/master/conf:/etc/mysql \ -e My…...

编程日记 2023/9/15 9:08:28

使用 AWS S3 SDK 访问 COS-腾讯云国际站代充

腾讯云国际站对象存储&#xff08;Cloud Object Storage&#xff0c;COS&#xff09;提供了 AWS S3 兼容的 API&#xff0c;因此当用户的数据从 S3 迁移到 COS 之后&#xff0c;只需要进行简单的配置修改&#xff0c;即可让客户端应用轻松兼容 COS 服务。下面unirech小编主要介…...

编程日记 2023/9/15 9:07:27

c语言每日一练(15)

前言&#xff1a;每日一练系列&#xff0c;每一期都包含5道选择题&#xff0c;2道编程题&#xff0c;博主会尽可能详细地进行讲解&#xff0c;令初学者也能听的清晰。每日一练系列会持续更新&#xff0c;上学期间将看学业情况更新。 五道选择题&#xff1a; 1、程序运行的结果…...

编程日记 2023/9/15 9:05:26

如何利用软文推广进行SEO优化（打造优质软文，提升网站排名）

在当今的互联网时代&#xff0c;SEO优化成为了网站推广的关键。而软文推广作为一种有效的推广方式&#xff0c;其优点不仅仅局限于SEO&#xff0c;还可以带来更多的曝光和用户流量。本文将深入探讨如何做好软文推广&#xff0c;从而提升网站排名和流量。 了解目标受众群体 内容…...

编程日记 2023/9/15 9:03:22

Java线程池ExecutorService和Executors应用(Spring Boot微服务)

记录&#xff1a;476 场景&#xff1a;在Spring Boot微服务中使用ExecutorService管理Java线程池。使用Executors创建线程池。使用Runnable接口实现类提交线程任务到线程池执行。 版本&#xff1a;JDK 1.8,Spring Boot 2.6.3。 1.线程和线程池基础 JDK自带线程和线程池包位…...

编程日记 2023/9/15 9:01:21

机器学习笔记之最优化理论与方法(八)无约束优化问题——常用求解方法(中)

机器学习笔记之最优化理论与方法——基于无约束优化问题的常用求解方法[中] 引言回顾&#xff1a;最速下降算法的缺陷经典牛顿法基本介绍经典牛顿法的问题经典牛顿法的优点与缺陷经典牛顿法示例 修正牛顿法介绍拟牛顿法拟牛顿法的算法过程 矩阵 B k 1 \mathcal B_{k1} Bk1​的…...

编程日记 2023/9/15 8:59:19

Django系列：Django简介与MTV架构体系概述

Django系列 Django简介与MTV架构体系概述 作者&#xff1a;李俊才 &#xff08;jcLee95&#xff09;&#xff1a;https://blog.csdn.net/qq_28550263 邮箱 &#xff1a;291148484163.com 本文地址&#xff1a;https://blog.csdn.net/qq_28550263/article/details/132890054 【介…...

编程日记 2023/9/15 8:58:18

锐捷交换机WEB管理系统EXCU_SHELL密码信息泄漏漏洞

一、漏洞简介 锐捷交换机 WEB 管理系统 EXCU_SHELL存在密码信息泄露漏洞&#xff0c;攻击者可从漏洞获取到管理员账号密码&#xff0c;从而以管理员权限登录。 二、影响版本 锐捷交换机 WEB 管理系统 三、资产测绘 hunterweb.body"img/free_login_ge.gif"&&…...

编程日记 2023/9/15 8:55:15

线性代数(六) 线性变换

前言 《线性空间》定义了空间&#xff0c;这章节来研究空间与空间的关联性 函数 函数是一个规则或映射&#xff0c;将一个集合中的每个元素&#xff08;称为自变量&#xff09;映射到另一个集合中的唯一元素&#xff08;称为因变量&#xff09;。 一般函数从 “A” 的每个元…...

编程日记 2023/9/15 8:52:13

Python基础运算分享

Python的运算符和其他语言类似 &#xff08;我们暂时只了解这些运算符的基本用法&#xff0c;方便我们展开后面的内容&#xff0c;高级应用暂时不介绍&#xff09; 数学运算 >>>print 19 # 加法>>>print 1.3-4 # 减法>>>print 3*5 …...

编程日记 2023/9/15 8:50:10

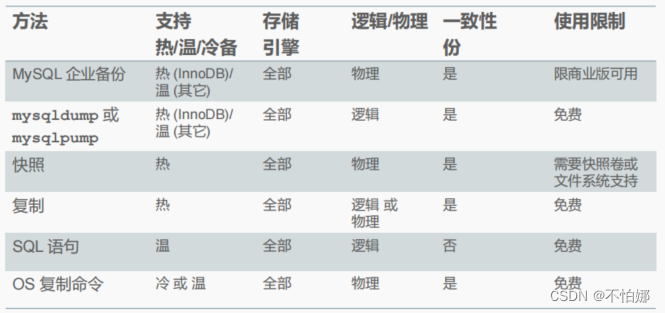
【MySQL】mysql中有哪几种类型的备份技术？它们各自有什么优缺点？

为什么要备份&#xff1f;备份类型&#xff08;从类型的角度&#xff09;备份技术&#xff08;从技术手段的角度&#xff09;不同备份方法的比较感谢 &#x1f496; 为什么要备份&#xff1f; 数据库或它所在的平台可能会出现问题&#xff0c;这时候数据库中的数据可能就遭到了…...

编程日记 2023/9/15 8:49:09

5基于pytorch的多目标粒子群算法，MOPSO,引导种群逼近真实Pareto前沿，算法运行结束后将外部存档中粒子作为获得的Pareto最优解近似。

基于pytorch的多目标粒子群算法&#xff0c;MOPSO,引导种群逼近真实Pareto前沿&#xff0c;算法运行结束后将外部存档中粒子作为获得的Pareto最优解近似。程序已调通&#xff0c;可以直接运行。 5pytorch多目标粒子群算法最优解5pytorch多目标粒子群算法最优解 (xiaohongshu.co…...

编程日记 2023/9/15 8:46:06

002 Linux 权限

前言 本文将会向您介绍关于linux权限方面的内容&#xff0c;包括文件类型&#xff0c;如何切换用户、基本权限、粘滞位等等 Linux具体的用户 超级用户&#xff1a;可以再linux系统下做任何事情&#xff0c;不受限制 普通用户&#xff1a;在linux下做有限的事情。 超级用户的…...

编程日记 2023/9/15 8:45:05

【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15

缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下&#xff1a; struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

编程新知 2025/11/27 21:52:13

深入浅出：JavaScript 中的 `window.crypto.getRandomValues()` 方法

深入浅出&#xff1a;JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中&#xff0c;随机数的生成看似简单&#xff0c;却隐藏着许多玄机。无论是生成密码、加密密钥&#xff0c;还是创建安全令牌&#xff0c;随机数的质量直接关系到系统的安全性。Jav…...

编程新知 2025/10/8 4:56:09

《用户共鸣指数（E）驱动品牌大模型种草：如何抢占大模型搜索结果情感高地》

在注意力分散、内容高度同质化的时代&#xff0c;情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现&#xff0c;消费者对内容的“有感”程度&#xff0c;正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中&#xff0…...

编程新知 2026/2/2 1:48:09

HBuilderX安装（uni-app和小程序开发）

下载HBuilderX 访问官方网站&#xff1a;https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本&#xff1a; Windows版&#xff08;推荐下载标准版&#xff09; Windows系统安装步骤 运行安装程序&#xff1a; 双击下载的.exe安装文件 如果出现安全提示&…...

编程新知 2026/1/31 12:52:04

【配置 YOLOX 用于按目录分类的图片数据集】

现在的图标点选越来越多&#xff0c;如何一步解决&#xff0c;采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集&#xff08;每个目录代表一个类别&#xff0c;目录下是该类别的所有图片&#xff09;&#xff0c;你需要进行以下配置步骤&#x…...

编程新知 2026/1/30 4:52:56

LLM基础1_语言模型如何处理文本

基于GitHub项目&#xff1a;https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken&#xff1a;OpenAI开发的专业"分词器" torch&#xff1a;Facebook开发的强力计算引擎&#xff0c;相当于超级计算器 理解词嵌入&#xff1a;给词语画"…...

编程新知 2025/9/25 5:16:24

python报错No module named ‘tensorflow.keras‘

是由于不同版本的tensorflow下的keras所在的路径不同&#xff0c;结合所安装的tensorflow的目录结构修改from语句即可。 原语句&#xff1a; from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后&#xff1a; from tensorflow.python.keras.lay…...

编程新知 2025/9/24 7:39:50

基于SpringBoot在线拍卖系统的设计和实现

摘 要 随着社会的发展&#xff0c;社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统&#xff0c;主要的模块包括管理员&#xff1b;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

编程新知 2026/1/26 13:25:02

【笔记】WSL 中 Rust 安装与测试完整记录

#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统&#xff1a;Ubuntu 24.04 LTS (WSL2)架构&#xff1a;x86_64 (GNU/Linux)Rust 版本&#xff1a;rustc 1.87.0 (2025-05-09)Cargo 版本&#xff1a;cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

编程新知 2026/1/26 14:15:48

【网络安全】开源系统getshell漏洞挖掘

审计过程&#xff1a; 在入口文件admin/index.php中&#xff1a; 用户可以通过m,c,a等参数控制加载的文件和方法&#xff0c;在app/system/entrance.php中存在重点代码&#xff1a; 当M_TYPE system并且M_MODULE include时&#xff0c;会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

编程新知 2026/1/31 2:59:25