第二十八章 Classes - 引用其他类的方法
文章目录
- 第二十八章 Classes - 引用其他类的方法
- 引用其他类的方法
- 对当前实例的引用
第二十八章 Classes - 引用其他类的方法
引用其他类的方法
在方法(或例程)中,使用下面的语法来引用其他类中的方法:
要调用类方法并访问其返回值,请使用如下表达式:
##class(Package.Class).MethodName(arguments)
iris.cls("Package.Class").MethodName(arguments)
例如:
Set x=##class(Util.Utils).GetToday()
x=iris.cls("Util.Utils").GetToday()
也可以调用一个类方法而不访问它的返回值,如下所示:
Do ##class(Util.Utils).DumpValues()
iris.cls("Util.Utils").DumpValues()
注意:##class不区分大小写。
- 要调用实例方法,创建一个实例,然后在
ObjectScript或Python中使用如下表达式来调用该方法并访问其返回值:
instance.MethodName(arguments)
例如:
Set x=instance.GetName()
x=instance.GetName()
你也可以在不访问返回值的情况下调用实例方法,方法如下:
Do instance.InsertItem("abc")
instance.InsertItem("abc")
并非所有方法都有返回值,因此请选择适合情况的语法。
对当前实例的引用
在实例方法中,有时需要引用当前实例本身,而不是实例的属性或方法。例如,在调用其他代码时,可能需要将当前实例作为参数传递。
在ObjectScript中,使用特殊变量$THIS来引用当前实例。在Python中,使用变量self来引用当前实例。
Set sc=header.ProcessService($this)
sc=header.ProcessService(self)
相关文章:

第二十八章 Classes - 引用其他类的方法
文章目录 第二十八章 Classes - 引用其他类的方法引用其他类的方法对当前实例的引用 第二十八章 Classes - 引用其他类的方法 引用其他类的方法 在方法(或例程)中,使用下面的语法来引用其他类中的方法: 要调用类方法并访问其返回值,请使用如下表达式:…...
Android 中集成 TensorFlow Lite图片识别
在上图通过手机的相机拍摄到的物体识别出具体的名称,这个需要通过TensorFlow 训练的模型引用到项目中;以下就是详细地集成 TensorFlow步骤,请按照以下步骤进行操作: 在项目的根目录下的 build.gradle 文件中添加 TensorFlow 的 Ma…...
NSSCTF之Misc篇刷题记录(16)
NSSCTF之Misc篇刷题记录(16) [黑盾杯 2020]encrypt[UTCTF 2020]Spectre[UTCTF 2020]Observe closely NSSCTF平台:https://www.nssctf.cn/ PS:所有FLAG改为NSSCTF [黑盾杯 2020]encrypt UTAxSlUwTkRWRVo3Um1GclpWOWxibU55ZVhCMGFX…...

域名解析--nslookup和dig
dig (Domain Information Groper) dig 是一个功能强大且更灵活的 DNS 查询工具,通常在 Linux 和 macOS 等 Unix-like 操作系统上使用。以下是 dig 的一些常见用法和区别: 查询域名信息 dig example.com这将返回与指定域名相关的 DNS 记录,…...
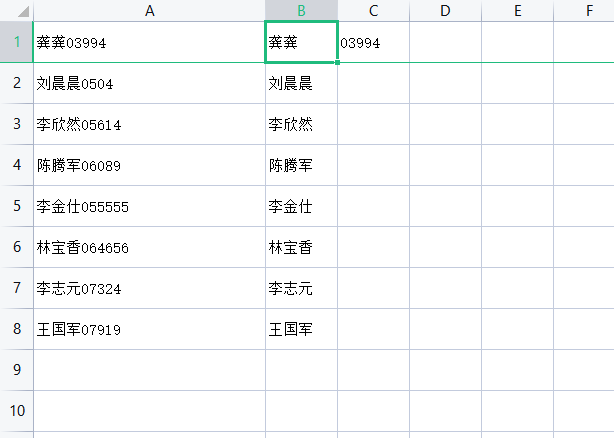
EXCEL如何把一个单元格内的文本和数字分开?例如:龚龚15565 = 龚龚 15565
使用工具:WPS 举例: EXCEL如何把一个单元格内的文本和数字批量分开?不使用数据分列。 第一步、将第二行数据冻结 第二步、在B1、C1单元格输入需要分开的示例 第三步、点击选中B1单元格,输入快捷键【CTRLE】进行填充。B2单元格也是…...
uniapp抽取组件绑定事件中箭头函数含花括号无法解析
版本: "dcloudio/uni-ui": "^1.4.27", "vue": "> 2.6.14 < 2.7"... 箭头函数后含有花括号的时候, getData就拿不到val参数 , 解决办法就是去除花括号 // 错误代码: <SearchComp change"(val) > { getData({ val …...

猫头虎博主第四期赠书活动:《精通Go语言:(第2版) 》
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

【学习总结】EasyExcel合并同列不同行,表格数据相同的行
实体类 Data HeadRowHeight(50) ContentStyle(horizontalAlignment HorizontalAlignmentEnum.CENTER, verticalAlignment VerticalAlignmentEnum.CENTER, wrapped BooleanEnum.TRUE) public class CriterionDataExportDTO {ColumnWidth(15)ExcelProperty(value "所属…...
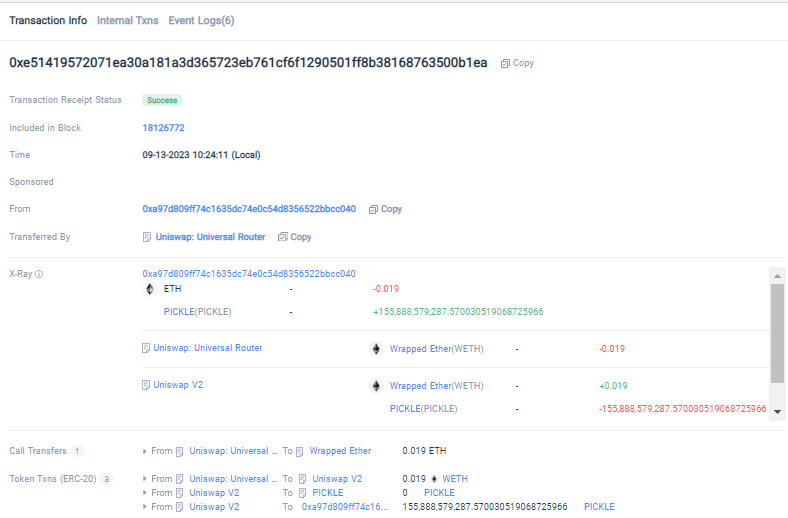
Tokenview X-ray功能:深入探索EVM系列浏览器的全新视角
Tokenview作为一家领先的多链区块浏览器,为了进一步优化区块链用户的使用体验,我们推出了X-ray(余额透视)功能。该功能将帮助您深入了解EVM系列浏览器上每个地址的交易过程,以一种直观、简洁的方式呈现地址的进出账情况…...
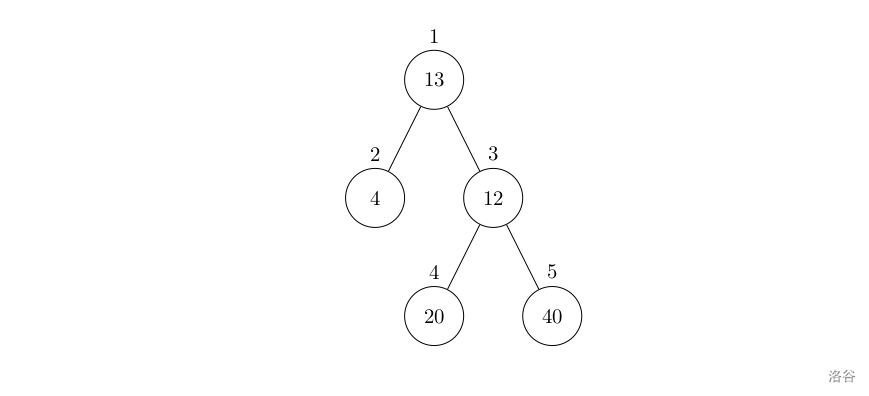
【洛谷 P1364】医院设置 题解(图论+深度优先搜索)
医院设置 题目描述 设有一棵二叉树,如图: 其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻接…...

【Java基础】- RMI原理和使用详解
【Java基础】- RMI原理和使用详解 文章目录 【Java基础】- RMI原理和使用详解一、什么RMI二、RMI原理2.1 工作原理图2.2 工作原理 三、RMI远程调用步骤3.1 RMI远程调用运行流程图3.2 RMI 远程调用步骤 四、JAVA RMI简单实现4.1 如何实现一个RMI程序4.2 JAVA实现RMI程序 一、什么…...

无水印免费4K视频素材网站 可商用-Free Stock Video
Free Stock Video是一个在线无水印免费4K视频素材网站,提供各种类型的4k、1080p的视频素材共免费下载,包括美食、水、自然、冬季、无人机、云朵、慢动作、夕阳、动态背景、缩时摄影、旅游和烟火,也可通过关键词搜索方式找到相关视频素材内容&…...

kubesphere中间件部署
微服务部署前中间件部署 一、MySQL部署 1.1 使用Docker实现MySQL主从复制 docker run -p 3307:3306 --name mysql-master \ -v /mydata/mysql/master/log:/var/log/mysql \ -v /mydata/mysql/master/data:/var/lib/mysql \ -v /mydata/mysql/master/conf:/etc/mysql \ -e My…...

使用 AWS S3 SDK 访问 COS-腾讯云国际站代充
腾讯云国际站对象存储(Cloud Object Storage,COS)提供了 AWS S3 兼容的 API,因此当用户的数据从 S3 迁移到 COS 之后,只需要进行简单的配置修改,即可让客户端应用轻松兼容 COS 服务。下面unirech小编主要介…...

c语言每日一练(15)
前言:每日一练系列,每一期都包含5道选择题,2道编程题,博主会尽可能详细地进行讲解,令初学者也能听的清晰。每日一练系列会持续更新,上学期间将看学业情况更新。 五道选择题: 1、程序运行的结果…...
如何利用软文推广进行SEO优化(打造优质软文,提升网站排名)
在当今的互联网时代,SEO优化成为了网站推广的关键。而软文推广作为一种有效的推广方式,其优点不仅仅局限于SEO,还可以带来更多的曝光和用户流量。本文将深入探讨如何做好软文推广,从而提升网站排名和流量。 了解目标受众群体 内容…...
)
Java线程池ExecutorService和Executors应用(Spring Boot微服务)
记录:476 场景:在Spring Boot微服务中使用ExecutorService管理Java线程池。使用Executors创建线程池。使用Runnable接口实现类提交线程任务到线程池执行。 版本:JDK 1.8,Spring Boot 2.6.3。 1.线程和线程池基础 JDK自带线程和线程池包位…...

机器学习笔记之最优化理论与方法(八)无约束优化问题——常用求解方法(中)
机器学习笔记之最优化理论与方法——基于无约束优化问题的常用求解方法[中] 引言回顾:最速下降算法的缺陷经典牛顿法基本介绍经典牛顿法的问题经典牛顿法的优点与缺陷经典牛顿法示例 修正牛顿法介绍拟牛顿法拟牛顿法的算法过程 矩阵 B k 1 \mathcal B_{k1} Bk1的…...

Django系列:Django简介与MTV架构体系概述
Django系列 Django简介与MTV架构体系概述 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/132890054 【介…...

锐捷交换机WEB管理系统EXCU_SHELL密码信息泄漏漏洞
一、漏洞简介 锐捷交换机 WEB 管理系统 EXCU_SHELL存在密码信息泄露漏洞,攻击者可从漏洞获取到管理员账号密码,从而以管理员权限登录。 二、影响版本 锐捷交换机 WEB 管理系统 三、资产测绘 hunterweb.body"img/free_login_ge.gif"&&…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...
