【物联网】简要介绍最小二乘法—C语言实现
最小二乘法是一种常用的数学方法,用于拟合数据和寻找最佳拟合曲线。它的目标是找到一个函数,使其在数据点上的误差平方和最小化。
文章目录
- 基本原理
- 最小二乘法的求解
- 应用举例
- 使用C语言实现最小二乘法
- 总结
基本原理
假设我们有一组数据点 ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) (x_1, y_1), (x_2, y_2), ..., (x_n, y_n) (x1,y1),(x2,y2),...,(xn,yn),我们想要找到一个函数 y = f ( x ) y = f(x) y=f(x),使得这个函数能够最好地拟合这些数据点。最小二乘法的基本思想是,我们要找到一个函数 y = f ( x ) y = f(x) y=f(x),使得所有数据点到这个函数的距离的平方和最小。
我们定义每个数据点到函数的距离为残差 r e s i d u a l i residual_i residuali,即 r e s i d u a l i = y i − f ( x i ) residual_i = y_i - f(x_i) residuali=yi−f(xi)。我们的目标是最小化所有残差的平方和,即最小化误差平方和 S = ∑ i = 1 n r e s i d u a l i 2 S = \sum_{i=1}^{n} residual_i^2 S=∑i=1nresiduali2。
最小二乘法的求解
为了求解最小二乘法问题,我们需要选择一个合适的函数形式 y = f ( x ) y = f(x) y=f(x)。常见的函数形式包括线性函数、多项式函数、指数函数等。以线性函数 y = a x + b y = ax + b y=ax+b为例,我们可以通过最小化误差平方和 S S S来求解系数 a a a和 b b b。
首先,我们定义一个目标函数 J ( a , b ) J(a, b) J(a,b),即 J ( a , b ) = ∑ i = 1 n ( y i − ( a x i + b ) ) 2 J(a, b) = \sum_{i=1}^{n} (y_i - (ax_i + b))^2 J(a,b)=∑i=1n(yi−(axi+b))2。我们的目标是找到使得 J ( a , b ) J(a, b) J(a,b)最小的 a a a和 b b b。为了达到这个目标,我们需要求解目标函数的偏导数,并令其为0。
对于目标函数 J ( a , b ) J(a, b) J(a,b),我们分别对 a a a和 b b b求偏导数,并令其为0,即:
∂ J ∂ a = 0 \frac{\partial J}{\partial a} = 0 ∂a∂J=0
∂ J ∂ b = 0 \frac{\partial J}{\partial b} = 0 ∂b∂J=0
通过求解上述方程组,我们可以得到 a a a和 b b b的解,从而得到最佳拟合直线。
应用举例
最小二乘法在实际应用中具有广泛的应用。例如,在经济学中,最小二乘法可以用于估计经济模型的参数。在物理学中,最小二乘法可以用于拟合实验数据并得到物理定律的参数。在机器学习中,最小二乘法可以用于线性回归问题。
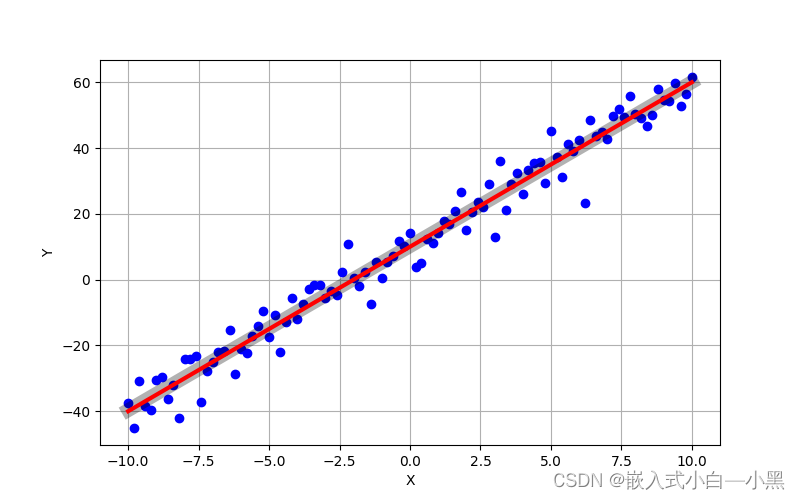
下面以线性回归问题为例,假设我们有一组房屋面积和价格的数据点,我们想要找到一个线性函数,使得能够最好地拟合这些数据点。我们可以使用最小二乘法来求解线性函数的参数。
假设我们的数据点为 ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) (x_1, y_1), (x_2, y_2), ..., (x_n, y_n) (x1,y1),(x2,y2),...,(xn,yn),我们要找到一个线性函数 y = a x + b y = ax + b y=ax+b,使得误差平方和 S = ∑ i = 1 n ( y i − ( a x i + b ) ) 2 S = \sum_{i=1}^{n} (y_i - (ax_i + b))^2 S=∑i=1n(yi−(axi+b))2最小化。
通过求解目标函数的偏导数,并令其为0,我们可以得到 a a a和 b b b的解。最终,我们可以得到最佳拟合直线的参数。
使用C语言实现最小二乘法
#include <stdio.h>// 定义最大数据点数量
#define MAX_DATA_POINTS 100// 定义数据点结构体
typedef struct {double x;double y;
} DataPoint;// 定义线性回归函数
void linearRegression(DataPoint* data, int n, double* a, double* b) {double sumX = 0, sumY = 0, sumXY = 0, sumX2 = 0;for (int i = 0; i < n; i++) {sumX += data[i].x;sumY += data[i].y;sumXY += data[i].x * data[i].y;sumX2 += data[i].x * data[i].x;}double denominator = n * sumX2 - sumX * sumX;*a = (n * sumXY - sumX * sumY) / denominator;*b = (sumY * sumX2 - sumX * sumXY) / denominator;
}int main() {int n;DataPoint data[MAX_DATA_POINTS];// 输入数据点数量printf("Enter the number of data points: ");scanf("%d", &n);// 输入数据点的 x 和 y 值printf("Enter the data points (x, y):\n");for (int i = 0; i < n; i++) {printf("Data point %d: ", i+1);scanf("%lf %lf", &data[i].x, &data[i].y);}double a, b;linearRegression(data, n, &a, &b);// 输出线性回归的结果printf("Linear regression equation: y = %.2fx + %.2f\n", a, b);return 0;
}
该代码实现了一个简单的线性回归函数linearRegression,该函数接受一个数据点数组和数据点数量作为输入,并计算出最佳拟合直线的参数。在main函数中,我们首先输入数据点的数量和具体数值,然后调用linearRegression函数进行线性回归计算,并输出最佳拟合直线的方程。
请注意,该代码仅实现了简单的线性回归,如果需要拟合其他类型的函数,需要相应地修改linearRegression函数的实现。
总结
最小二乘法是一种常用的数学方法,用于拟合数据和寻找最佳拟合曲线。它的基本原理是最小化数据点到拟合函数的距离的平方和。通过求解目标函数的偏导数,并令其为0,我们可以得到最佳拟合函数的参数。最小二乘法在各个领域都有广泛的应用,是一种非常有用的工具。
相关文章:
【物联网】简要介绍最小二乘法—C语言实现
最小二乘法是一种常用的数学方法,用于拟合数据和寻找最佳拟合曲线。它的目标是找到一个函数,使其在数据点上的误差平方和最小化。 文章目录 基本原理最小二乘法的求解应用举例使用C语言实现最小二乘法总结 基本原理 假设我们有一组数据点 ( x 1 , y 1 …...

慢查询SQL如何优化
一.什么是慢SQL? 慢SQL指的是Mysql中执行比较慢的SQL,排查慢SQL最常用的方法是通过慢查询日志来查找慢SQL。Mysql的慢查询日志是Mysql提供的一种日志记录,它用来记录Mysql中响应时间超过long_query_time值的sql,long_query_time的默认时间为10s. 二.查看慢SQL是否…...

UART 通信-使用VIO进行板级验证
串口系列知识分享: (1)串口通信实现-串口发送 (2)串口通信发送多字节数据 (3)串口通信实现-串口接收 (4)UART 通信-使用VIO进行板级验证 (5)串口接收-控制LED闪烁 (6)使用串口发送实现ACX720开发板时钟显示 (7)串口发送+RAM+VGA传图 文章目录 前言一、uart串口协…...

linux 查看可支持的shell
查看可支持的shell linux中支持多种shell类型,所以在shell文件的第一行需要指定所使用的shell #!/bin/bash 指定该脚本使用的是/bin/bash,这样的机制使得我们可以轻松地引用任何的解释器 查看该linux系统支持的shell cat /etc/shells/bin/sh/bin/bash/us…...

微服务简介
微服务简介 微服务架构是一种软件架构模式,它将一个大型应用程序拆分为一组小型、独立的服务,每个服务都有自己的业务逻辑和数据存储。这些服务可以独立开发、部署和扩展,通常使用HTTP或其他轻量级通信协议进行通信。 以下是微服务架构的一…...
PHP自己的框架2.0设置常量并绑定容器(重构篇三)
目录 1、设置常量并绑定容器 2、容器增加设置当前容器的实例和绑定一个类实例当容器 3、将常量绑定到容器中 4、运行效果 1、设置常量并绑定容器 2、容器增加设置当前容器的实例和绑定一个类实例当容器 //设置当前容器的实例public static function setInstance($instance){…...

重建大师提交空三后引擎状态是等待,怎么开启?
答:图片中这是在自由网空三阶段,整个AT都是等待中,可以修改任务目录和监控目录看一下,先设置引擎,再提交空三。...
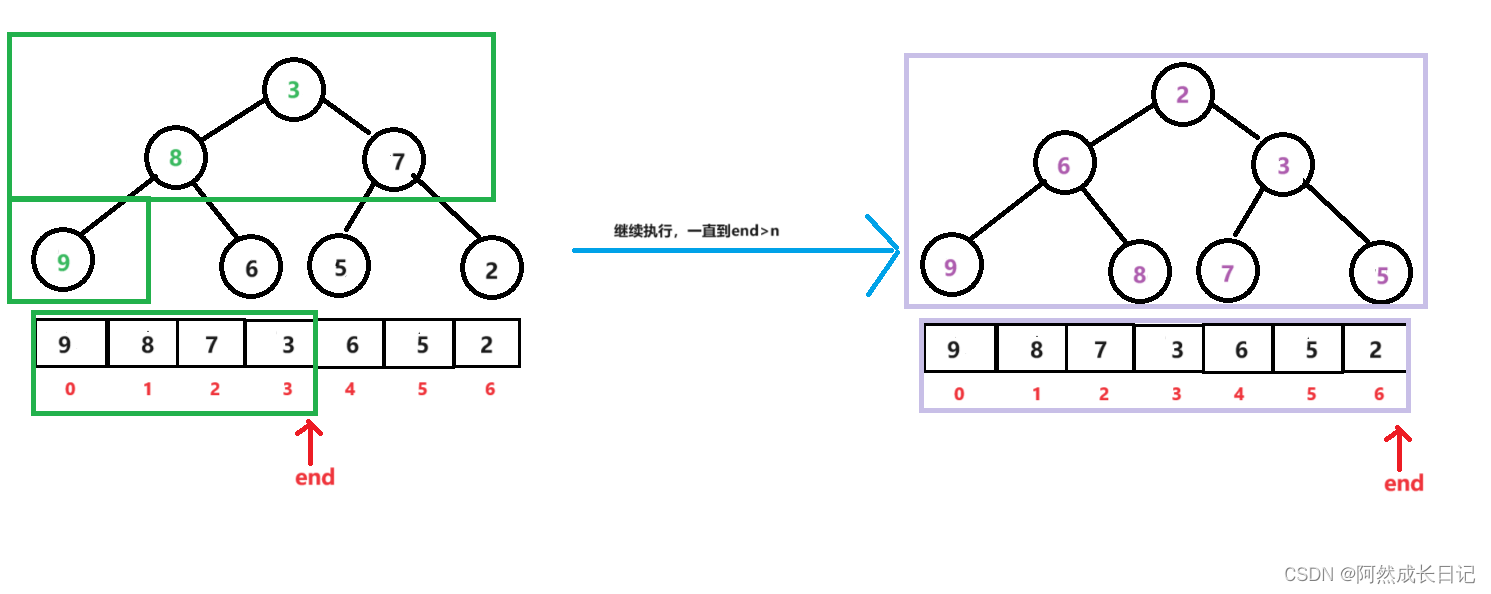
【数据结构】堆的向上调整和向下调整以及相关方法
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃 文章目录 一、堆的概念二、堆的性质…...

【蓝桥杯选拔赛真题60】Scratch旋转风车 少儿编程scratch图形化编程 蓝桥杯选拔赛真题解析
目录 scratch旋转风车 一、题目要求 编程实现 二、案例分析 1、角色分析...

JavaSE、JavaEE与Spring的概念和异同点剖析以及规范13 个分析
JavaSE、JavaEE与Spring的概念和异同点剖析以及规范13 个分析 目录概述需求: 设计思路实现思路分析1.什么是JavaSE2.是JavaEE3.什么是Spring 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy&…...
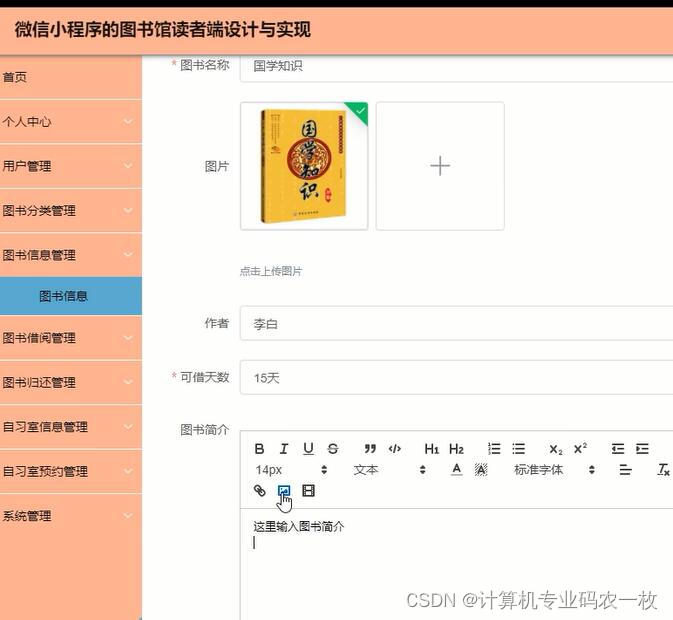
微信小程序的图书馆图书借阅 座位预约系统 读者端设计与实现
该系统基于B/S即所谓浏览器/服务器模式,应用springboot框架,选择MySQL作为后台数据库。系统主要包括系统图书信息、图书借阅、图书归还、自习室信息、自习室预约等功能模块。 关键词 微信小程序的图书馆读者端;微信小程序;java语…...
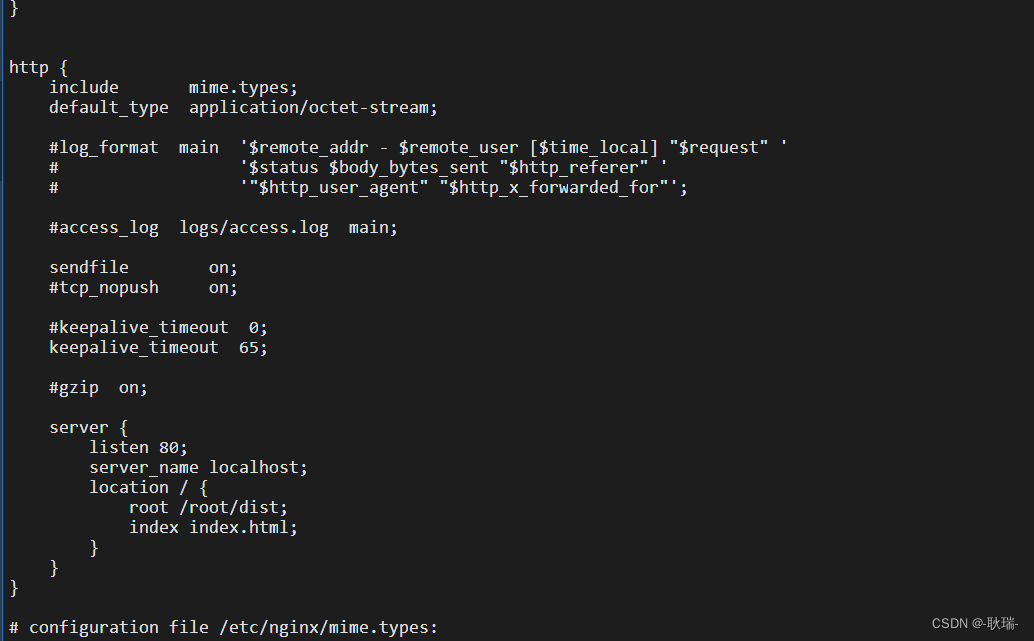
在阿里云 linux 服务器上查看当前服务器的Nginx配置信息
我们可以通过命令 sudo nginx -t查看到nginx.conf的路径 可以通过 sudo nginx -T查看 nginx 详细配置信息,包括加载的配置文件和配置块的内容 其中也会包括配置文件的内容...

专业招投标书翻译怎样做比较好
在全球经济贸易一体化不断深入的时代,招投标作为国际通用的新型贸易方式,受到了大量中外企业的青睐。根据国际惯例,与招标采购活动有关的一切文件资料,均须使用英文编制。即使允许使用非英文语言编制,也必须随附一份英…...
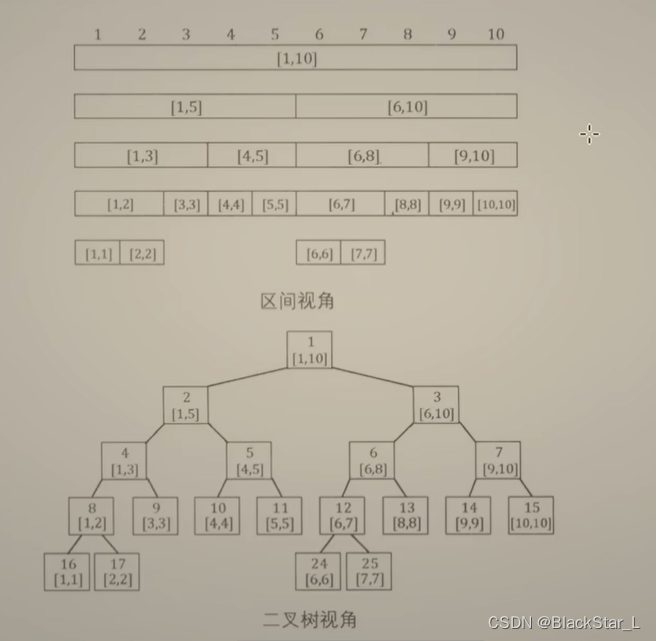
算法总结10 线段树
算法总结10 线段树 线段树2569. 更新数组后处理求和查询 线段树 有一个数组,我们要: 更新数组的值(例如:都加上一个数,把子数组内的元素取反)查询一个子数组的值(例如:求和&#x…...

518抽奖软件,支持按人像照片抽奖
518抽奖软件简介 518抽奖软件,518我要发,超好用的年会抽奖软件,简约设计风格。 包含文字号码抽奖、照片抽奖两种模式,支持姓名抽奖、号码抽奖、数字抽奖、照片抽奖。(www.518cj.net) 照片抽奖模式 圆角边框 照片抽奖模式下&am…...
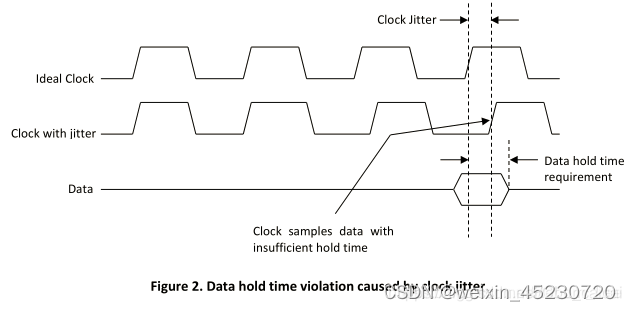
数字IC笔试面试题之--时钟偏斜(skew)与抖动(jitter)
1 时钟偏斜(clock skew) 时钟偏斜(偏移)是因为布线长度和负载不同,导致同一时钟上升沿到不同触发器的时间不同。这一时间差,即为时钟偏移。 时钟偏斜可能导致时序违例(本文直接粘贴了参考博客…...

免费api接口:物流api,企业工商查询api,游戏api。。。
免费api接口,物流api,企业工商查询api,游戏api。。。都有。 Facebook Games Services - Facebook Games Services 为游戏开发者提供了各种服务, 包括(但不限于) 成就 API, 分数 API, 应用通知, 请求, 游戏养成和 Facebook SDK for Unity.Google Play Games Service…...

第二十八章 Classes - 引用其他类的方法
文章目录 第二十八章 Classes - 引用其他类的方法引用其他类的方法对当前实例的引用 第二十八章 Classes - 引用其他类的方法 引用其他类的方法 在方法(或例程)中,使用下面的语法来引用其他类中的方法: 要调用类方法并访问其返回值,请使用如下表达式:…...
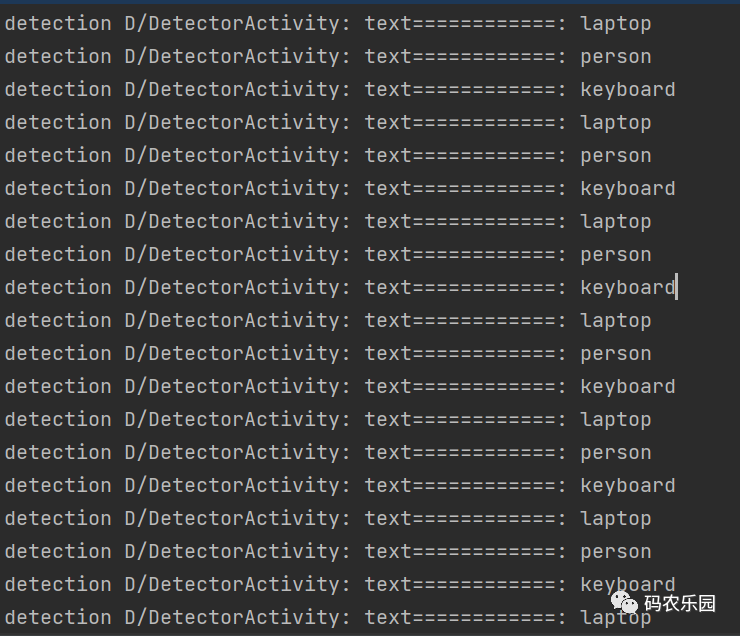
Android 中集成 TensorFlow Lite图片识别
在上图通过手机的相机拍摄到的物体识别出具体的名称,这个需要通过TensorFlow 训练的模型引用到项目中;以下就是详细地集成 TensorFlow步骤,请按照以下步骤进行操作: 在项目的根目录下的 build.gradle 文件中添加 TensorFlow 的 Ma…...
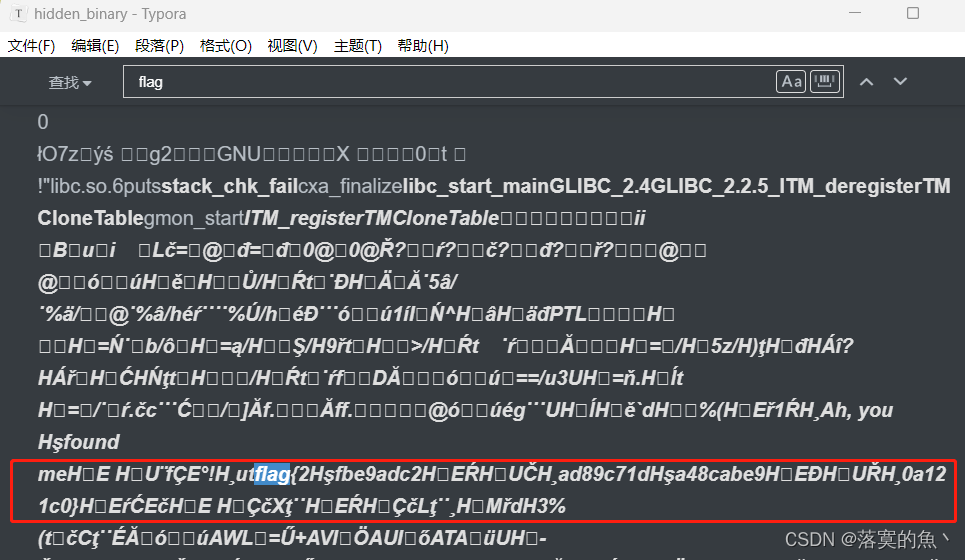
NSSCTF之Misc篇刷题记录(16)
NSSCTF之Misc篇刷题记录(16) [黑盾杯 2020]encrypt[UTCTF 2020]Spectre[UTCTF 2020]Observe closely NSSCTF平台:https://www.nssctf.cn/ PS:所有FLAG改为NSSCTF [黑盾杯 2020]encrypt UTAxSlUwTkRWRVo3Um1GclpWOWxibU55ZVhCMGFX…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...
