【数据结构】堆的向上调整和向下调整以及相关方法

💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤
📃文章目录
- 一、堆的概念
- 二、堆的性质
- 三、堆的分类
- 1.大根堆
- 2.小根堆
- 四、说明
- 五、堆的结构
- 🚩六、堆的向上调整
- 1.图示
- 2.代码实现
- ⌚️3.时间复杂度分析
- 📌七、堆的向下调整
- 1.思路:
- 2.代码实现
- ⌚️3.时间复杂度分析
- 八、删除根
- 1.思路:
- 2.代码实现
- ⌚️3.时间复杂度分析
- 九、创建堆
- 1.思路:
- 2.代码实现
- 十、所有方法实现汇总
一、堆的概念
堆(Heap)是计算机科学中一类特殊的数据结构的统称。如果有一个关键码的集合K = { , , ,…, },把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足: <= 且 <= ( >= 且 >= ) i = 0,1, 2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。除了最后一层以外上面的节点但是非空的,最后一层节点是从左到右依次排布的)
二、堆的性质
🔸 非线性,完全二叉树。适合用数组存储。
🔸堆是无序的,也就是左右可以互换
🔸最值总在 0 号位
根据这个特点我们就可以做很多事情,比如TopK问题 (在一堆数据里面找到前 K 个最大 / 最小的数).
比如点餐软件中有上千家店铺,我想选出该地区好评最多的十家川菜店,我们不用对所有数据排序,只需要取出前 K 个最大 / 最小数据。使用堆排序效率也更高。
三、堆的分类
1.大根堆 2.小根堆
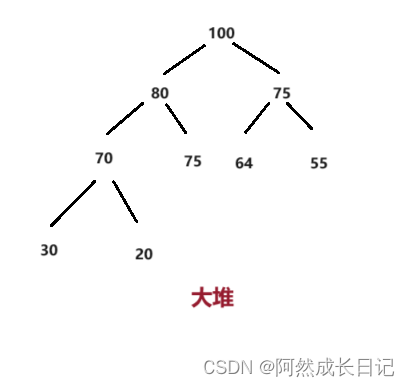
1.大根堆
定义:树中的任意一个双亲节点都大于等于孩子节点。
2.小根堆
定义:树中的任意一个双亲节点都小于等于孩子节点。
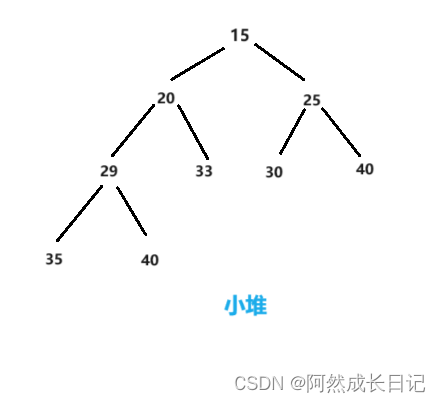
四、说明
以下的方法均以小堆来推理,如果想实现大堆,则修改【<】符号等方式实现。
五、堆的结构
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;
🚩六、堆的向上调整
向上调整的前提是,调整位置之前必须是堆。如果目的是调成小堆,则要保证调整位置之前是小堆;如果目的是调成大堆,则要保证调整位置之前是大堆。
1.图示
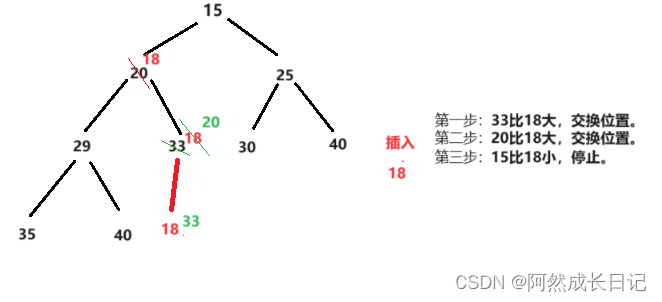
2.代码实现
//向上调整
void AdjustUp(HPDataType* a, int child)
{//传入数组,child为孩子节点下标int parent = (child - 1) / 2;//当一直交换到根,停止while (child>0){if (a[parent] > a[child]){Swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}elsereturn;}
}
⌚️3.时间复杂度分析
时间复杂度:O(logN)
最坏情况:调整到根;
最好情况:不用调整,
📌七、堆的向下调整
向下调整的前提是,左右子树必须是小堆或者大堆。
1.思路:
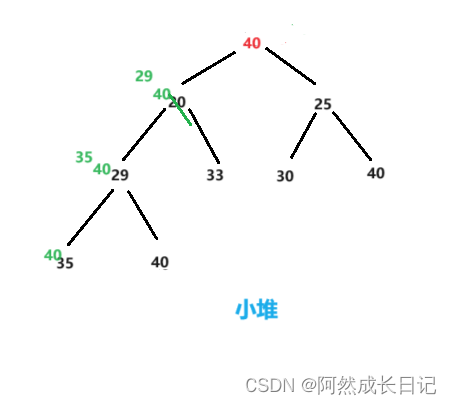
如图:
此案例是要调整根节点40开始向下调整,首先确保根节点的左右子树是小堆(由图得成立)。
1.parent的两个孩子进行比较,选出小的。
2.进行交换
3.child>n结束
2.代码实现
//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;//一直交换到数的最后,也就是数组的最后一个位置while (parent<n){if (child + 1 < n && a[child + 1] < a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);// 继续往下调整parent = child;child = parent * 2 + 1;}else{return;}}
}
⌚️3.时间复杂度分析
时间复杂度:O(logN)
最坏情况:调整到根;
最好情况:不用调整,
八、删除根
1.思路:
1.先将根与最后一个节点交换,
2.删除最后一个节点;
3.进行向下调整。

2.代码实现
void HeapPop(HP* p)
{assert(p);assert(p->size > 0);Swap(&p->a[0], &p->a[p->size - 1]);--p->size;AdjustDown(p->a, p->size, 0);
}
⌚️3.时间复杂度分析
时间复杂度:O:N(logN)
九、创建堆
创建堆的思路可以通过向上调整,也可通过向下调整。这里讲通过向上调整建立堆。
由于我的AdjustUp函数是用来调整小堆的,所以,这里创建的也是小堆。
1.思路:
传入参数
a:数组,n:是数组元素个数
1.为p->a开辟n个空间;
2.利用memcpy函数,把数组a复制到p->a中
3.在使用AdjustUp调整,从1-n-1逐步向下延伸;
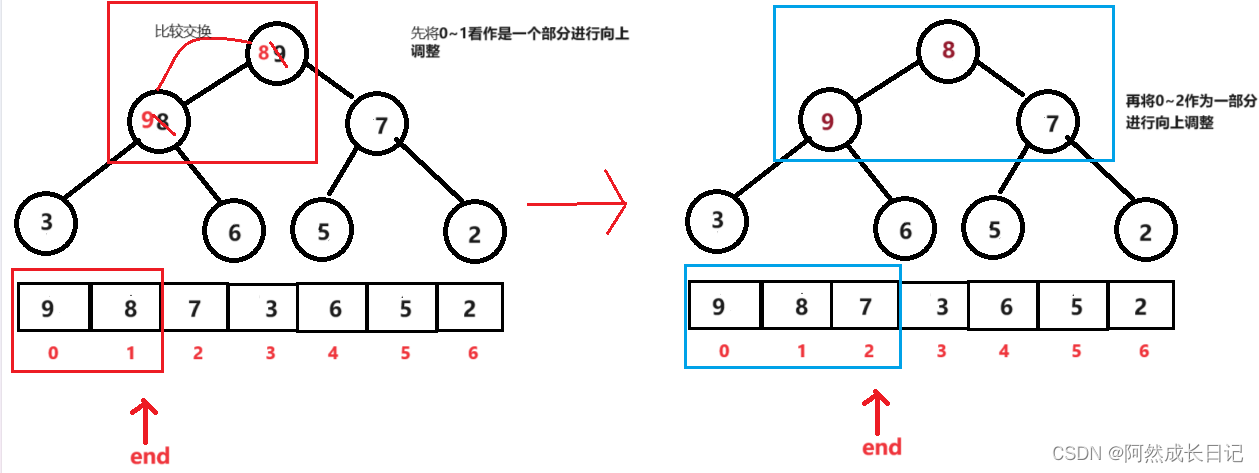
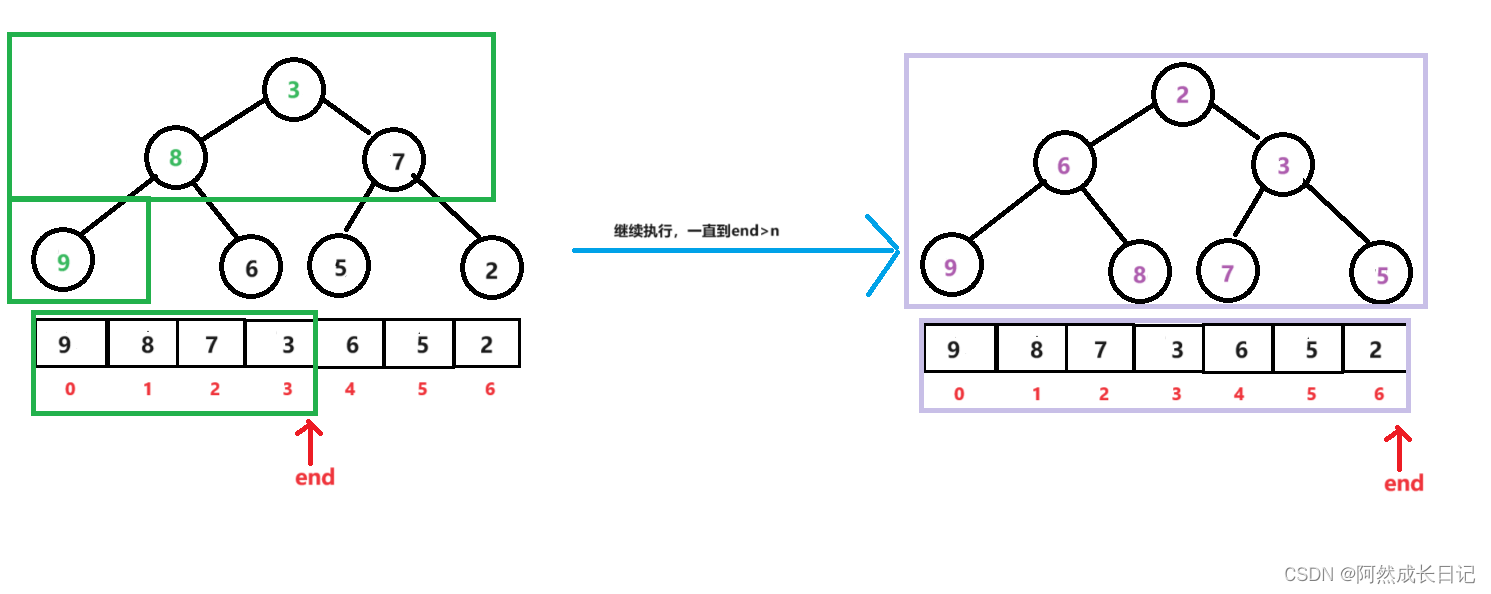
2.代码实现
//建立小堆
void HeapInitArray(HP* p, int* a, int n)
{//a:数组,n:是数组元素个数assert(p);assert(a);p->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (p->a == NULL){perror("malloc fail");exit(-1);}p->size = n;p->capacity = n;//把传入数组a复制到p->a中memcpy(p->a, a, sizeof(HPDataType) * n);// 向上调整,调整成一个小堆for (int i = 1; i < n; i++){AdjustUp(p->a, i);}
}
十、所有方法实现汇总
#define _CRT_SECURE_NO_WARNINGS 1
#include"Heap.h"//初始化
void HeapInit(HP* p)
{assert(p);p->a = NULL;p->size = 0;p->capacity = 0;
}//销毁
void HeapDestroy(HP* p)
{assert(p);free(p->a);p->a = NULL;p->size = p->capacity = 0;
}//插入数据
void HeapPush(HP* p, HPDataType x)
{//从最后一个位置插入assert(p);//扩容if (p->capacity == p->size){//如果刚开始数组为空,就开辟4个空间。如果不为空,以后每次扩大2倍。int newcapacity = p->capacity==0 ? 4 : p->capacity * 2;HPDataType* tmp = (HPDataType*)realloc(p->a, sizeof(HPDataType) * p->capacity);if (tmp == NULL){perror("realloc fial\n");exit(-1);}p->a = tmp;p->capacity = newcapacity;}p->a[p->size] = x;p->size++;AdjustUp(p->a, p->size-1);
}//交换
void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}//向上调整
void AdjustUp(HPDataType* a, int child)
{//传入数组,child为孩子节点下标int parent = (child - 1) / 2;//当一直交换到根,停止while (child>0){if (a[parent] > a[child]){Swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}elsereturn;}
}//向下调整
void AdjustDown(HPDataType* a, int n, int parent)
{int child = parent * 2 + 1;//一直交换到数的最后,也就是数组的最后一个位置while (parent<n){if (child + 1 < n && a[child + 1] < a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);// 继续往下调整parent = child;child = parent * 2 + 1;}else{return;}}
}//打印二叉树
void HeapPrint(HP* php)
{assert(php);for (size_t i = 0; i < php->size; i++){printf("%d ", php->a[i]);}printf("\n");
}//建立小堆
void HeapInitArray(HP* p, int* a, int n)
{//a:数组,n:是数组元素个数assert(p);assert(a);p->a = (HPDataType*)malloc(sizeof(HPDataType) * n);if (p->a == NULL){perror("malloc fail");exit(-1);}p->size = n;p->capacity = n;//把传入数组a复制到p->a中memcpy(p->a, a, sizeof(HPDataType) * n);// 向上调整,调整成一个小堆for (int i = 1; i < n; i++){AdjustUp(p->a, i);}
}//删除根
void HeapPop(HP* p)
{assert(p);assert(p->size > 0);Swap(&p->a[0], &p->a[p->size - 1]);--p->size;AdjustDown(p->a, p->size, 0);
}
//获取根
HPDataType HeapTop(HP* p)
{assert(p);assert(p->size > 0);return p->a[0];
}//判空
bool HeapEmpty(HP* p)
{assert(p);return p->size == 0;
}
相关文章:

【数据结构】堆的向上调整和向下调整以及相关方法
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃 文章目录 一、堆的概念二、堆的性质…...

【蓝桥杯选拔赛真题60】Scratch旋转风车 少儿编程scratch图形化编程 蓝桥杯选拔赛真题解析
目录 scratch旋转风车 一、题目要求 编程实现 二、案例分析 1、角色分析...

JavaSE、JavaEE与Spring的概念和异同点剖析以及规范13 个分析
JavaSE、JavaEE与Spring的概念和异同点剖析以及规范13 个分析 目录概述需求: 设计思路实现思路分析1.什么是JavaSE2.是JavaEE3.什么是Spring 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy&…...
微信小程序的图书馆图书借阅 座位预约系统 读者端设计与实现
该系统基于B/S即所谓浏览器/服务器模式,应用springboot框架,选择MySQL作为后台数据库。系统主要包括系统图书信息、图书借阅、图书归还、自习室信息、自习室预约等功能模块。 关键词 微信小程序的图书馆读者端;微信小程序;java语…...
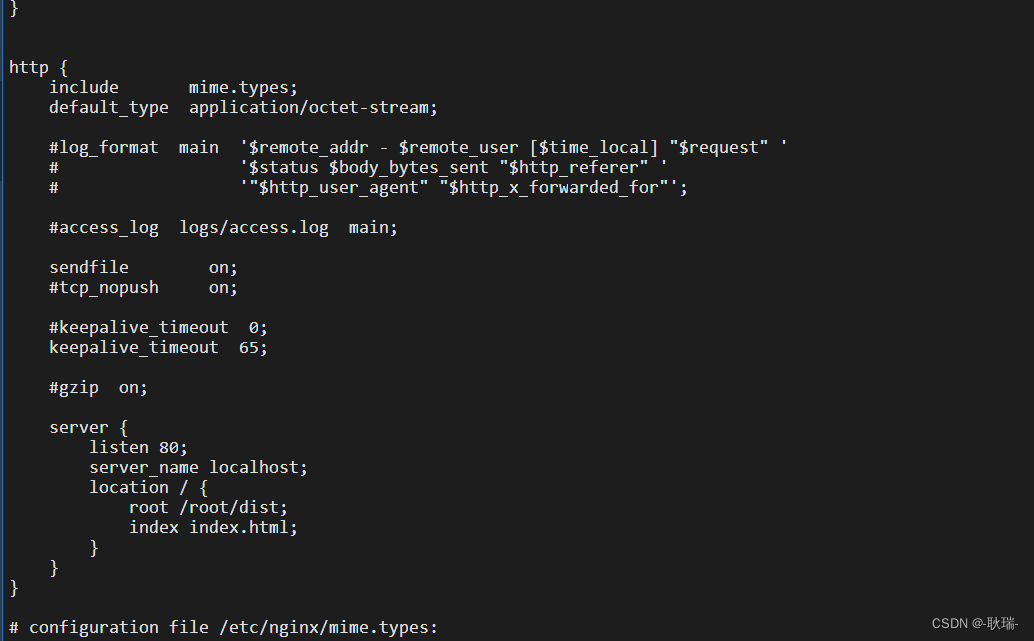
在阿里云 linux 服务器上查看当前服务器的Nginx配置信息
我们可以通过命令 sudo nginx -t查看到nginx.conf的路径 可以通过 sudo nginx -T查看 nginx 详细配置信息,包括加载的配置文件和配置块的内容 其中也会包括配置文件的内容...

专业招投标书翻译怎样做比较好
在全球经济贸易一体化不断深入的时代,招投标作为国际通用的新型贸易方式,受到了大量中外企业的青睐。根据国际惯例,与招标采购活动有关的一切文件资料,均须使用英文编制。即使允许使用非英文语言编制,也必须随附一份英…...
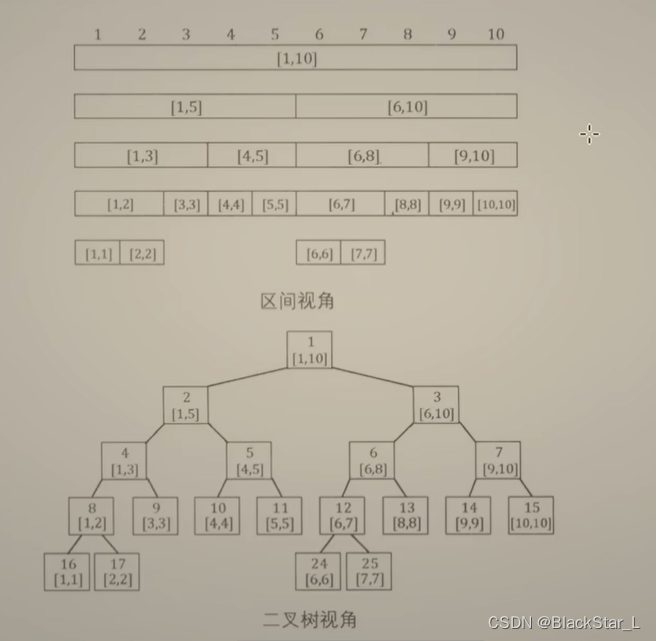
算法总结10 线段树
算法总结10 线段树 线段树2569. 更新数组后处理求和查询 线段树 有一个数组,我们要: 更新数组的值(例如:都加上一个数,把子数组内的元素取反)查询一个子数组的值(例如:求和&#x…...

518抽奖软件,支持按人像照片抽奖
518抽奖软件简介 518抽奖软件,518我要发,超好用的年会抽奖软件,简约设计风格。 包含文字号码抽奖、照片抽奖两种模式,支持姓名抽奖、号码抽奖、数字抽奖、照片抽奖。(www.518cj.net) 照片抽奖模式 圆角边框 照片抽奖模式下&am…...
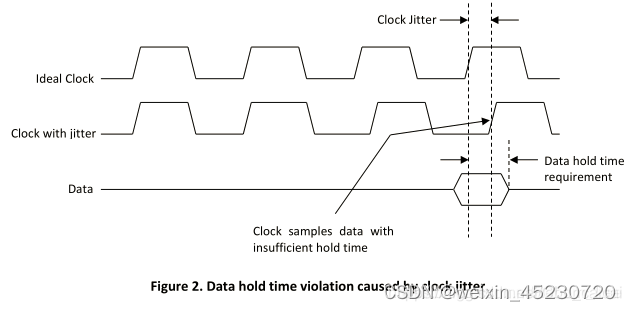
数字IC笔试面试题之--时钟偏斜(skew)与抖动(jitter)
1 时钟偏斜(clock skew) 时钟偏斜(偏移)是因为布线长度和负载不同,导致同一时钟上升沿到不同触发器的时间不同。这一时间差,即为时钟偏移。 时钟偏斜可能导致时序违例(本文直接粘贴了参考博客…...

免费api接口:物流api,企业工商查询api,游戏api。。。
免费api接口,物流api,企业工商查询api,游戏api。。。都有。 Facebook Games Services - Facebook Games Services 为游戏开发者提供了各种服务, 包括(但不限于) 成就 API, 分数 API, 应用通知, 请求, 游戏养成和 Facebook SDK for Unity.Google Play Games Service…...

第二十八章 Classes - 引用其他类的方法
文章目录 第二十八章 Classes - 引用其他类的方法引用其他类的方法对当前实例的引用 第二十八章 Classes - 引用其他类的方法 引用其他类的方法 在方法(或例程)中,使用下面的语法来引用其他类中的方法: 要调用类方法并访问其返回值,请使用如下表达式:…...
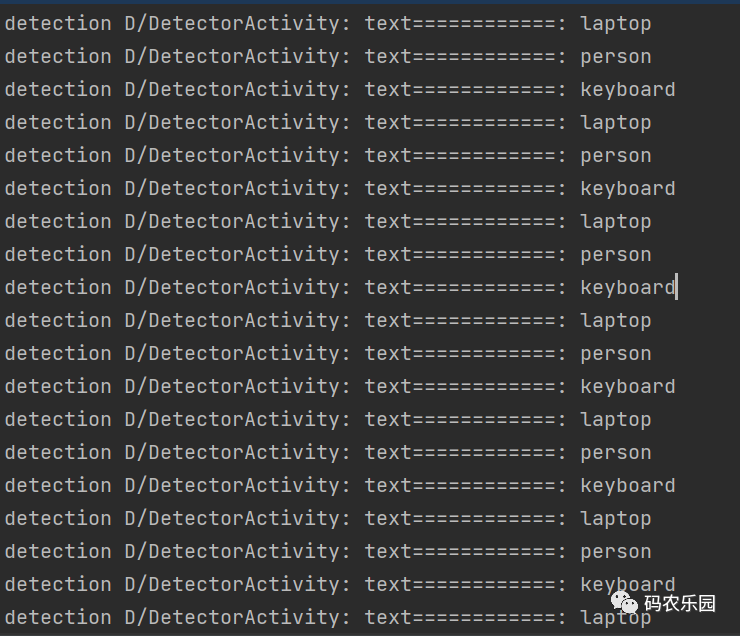
Android 中集成 TensorFlow Lite图片识别
在上图通过手机的相机拍摄到的物体识别出具体的名称,这个需要通过TensorFlow 训练的模型引用到项目中;以下就是详细地集成 TensorFlow步骤,请按照以下步骤进行操作: 在项目的根目录下的 build.gradle 文件中添加 TensorFlow 的 Ma…...
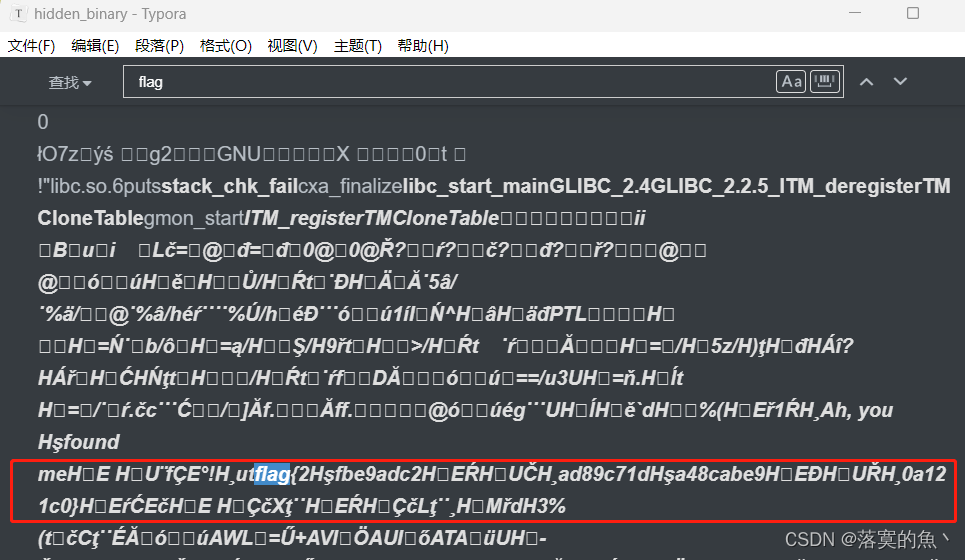
NSSCTF之Misc篇刷题记录(16)
NSSCTF之Misc篇刷题记录(16) [黑盾杯 2020]encrypt[UTCTF 2020]Spectre[UTCTF 2020]Observe closely NSSCTF平台:https://www.nssctf.cn/ PS:所有FLAG改为NSSCTF [黑盾杯 2020]encrypt UTAxSlUwTkRWRVo3Um1GclpWOWxibU55ZVhCMGFX…...

域名解析--nslookup和dig
dig (Domain Information Groper) dig 是一个功能强大且更灵活的 DNS 查询工具,通常在 Linux 和 macOS 等 Unix-like 操作系统上使用。以下是 dig 的一些常见用法和区别: 查询域名信息 dig example.com这将返回与指定域名相关的 DNS 记录,…...
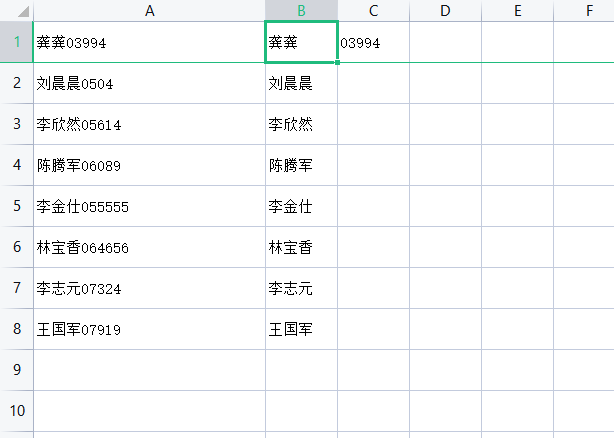
EXCEL如何把一个单元格内的文本和数字分开?例如:龚龚15565 = 龚龚 15565
使用工具:WPS 举例: EXCEL如何把一个单元格内的文本和数字批量分开?不使用数据分列。 第一步、将第二行数据冻结 第二步、在B1、C1单元格输入需要分开的示例 第三步、点击选中B1单元格,输入快捷键【CTRLE】进行填充。B2单元格也是…...
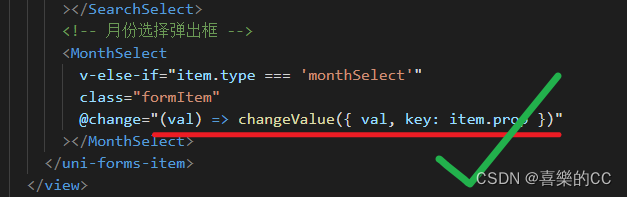
uniapp抽取组件绑定事件中箭头函数含花括号无法解析
版本: "dcloudio/uni-ui": "^1.4.27", "vue": "> 2.6.14 < 2.7"... 箭头函数后含有花括号的时候, getData就拿不到val参数 , 解决办法就是去除花括号 // 错误代码: <SearchComp change"(val) > { getData({ val …...

猫头虎博主第四期赠书活动:《精通Go语言:(第2版) 》
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

【学习总结】EasyExcel合并同列不同行,表格数据相同的行
实体类 Data HeadRowHeight(50) ContentStyle(horizontalAlignment HorizontalAlignmentEnum.CENTER, verticalAlignment VerticalAlignmentEnum.CENTER, wrapped BooleanEnum.TRUE) public class CriterionDataExportDTO {ColumnWidth(15)ExcelProperty(value "所属…...
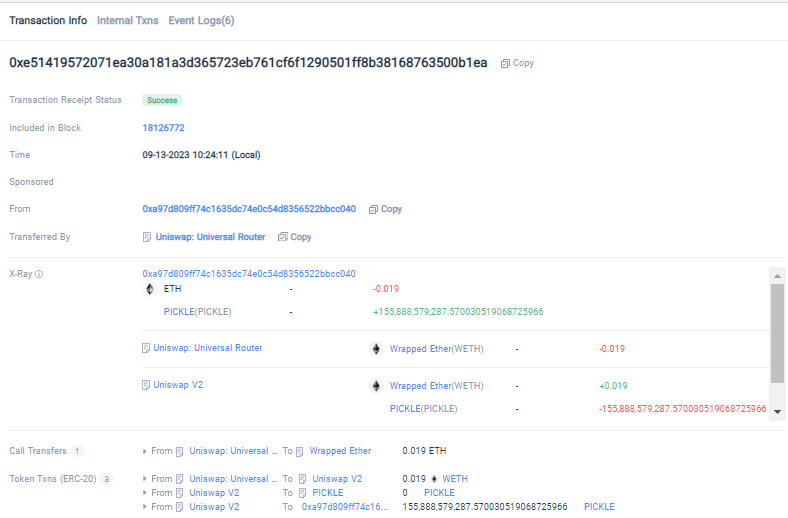
Tokenview X-ray功能:深入探索EVM系列浏览器的全新视角
Tokenview作为一家领先的多链区块浏览器,为了进一步优化区块链用户的使用体验,我们推出了X-ray(余额透视)功能。该功能将帮助您深入了解EVM系列浏览器上每个地址的交易过程,以一种直观、简洁的方式呈现地址的进出账情况…...
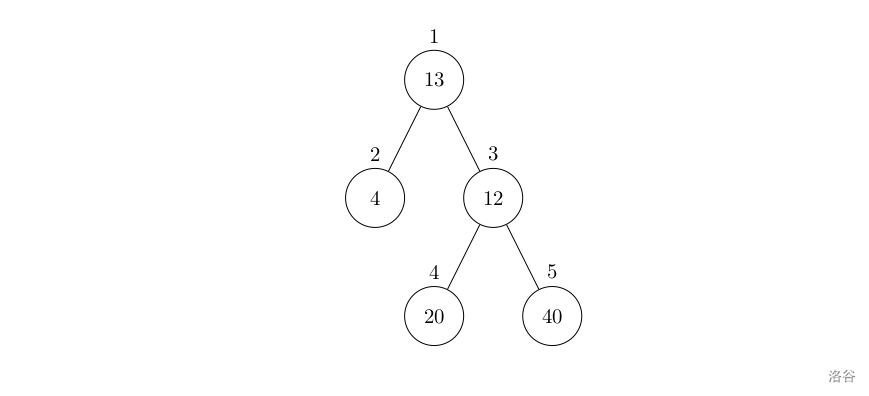
【洛谷 P1364】医院设置 题解(图论+深度优先搜索)
医院设置 题目描述 设有一棵二叉树,如图: 其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻接…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
