kubernetes集群yaml文件与kubectl工具
k8s集群中对资源管理和资源对象编排部署都可以通过声明样式(yaml)文件来解决,也就是可以把需要对资源对象操作编辑到yaml格式文件中,我们把文件叫做资源清单文件,通过kubectl命令直接使用资源清单文件就可以实现对大量的资源对象进行编排部署了。
yaml文件书写格式
yaml基本语法
- 使用空格作为缩进
- 缩进的空格数目不重要,只要相同层级的元素左侧对齐即可
- 低版本缩进时不允许使用Tab键,只允许使用空格
- 使用#标识注释,从这个字符一直到行尾,都会被解释器忽略
- 使用 —表示新的yaml文件开始
yaml支持的数据结构
- 对象
键值对的集合,又称为映射/哈希/字典
#对象类型:对象的一组键值对,使用冒号结构表示
apiVersion: apps/v1
kind: Deployment
- 数组
一组按次序排列的值,又称为序列/列表
# 数组类型:一组连词线开头的行,构成一个数组ports:- protocol: TCP
- 纯量
单个的、最基本的不可再分的值
# 数值直接以字面量的形似表示
number:12.90# 布尔值用true和false表示
isSet: true# null用~表示
parent: ~# 时间采用ISO8601格式
iso8601: 2021-12-12t21:39:43.10-05:00# 日期采用复合iso8601格式的年、月、日表示
date:1921-09-01# 字符串默认不使用引号表示
str :这是一个字符串#如果字符串之中包含空格或特殊字符,需要放在引号之中
str:'内容: 顶顶顶'# 单引号之中如果还有单引号,必须连续使用两个单引号转义
str:'labor ''s day'# 单引号和双引号都可以使用,双引号不会对特殊字符转义
s1:'内容\n字符串'
s2:"内容\n字符串"# 字符串可以写成多行,从第二行开始,必须有一个单空格缩进。换行符会被转为空格
str: 这是一段多行字符串kubectl工具
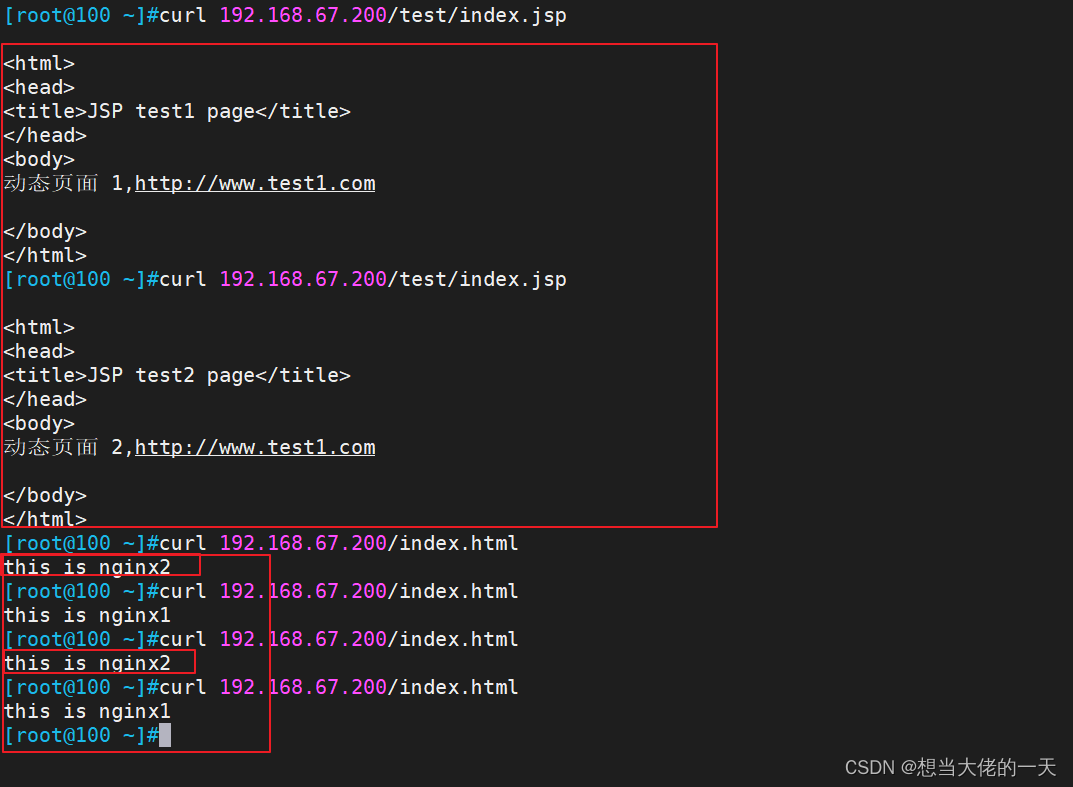
kubectl工具是k8s集群的命令行工具,通过kubectl工具能够对集群本身进行管理,并能够在集群上进行容器化应用的安装部署。
- kubectl命令的语法
kubectl [command] [TYPE] [NAME] [flags]
- command:指定要对资源执行的操作,例如create、get、set、delete。
- type:指定资源类型,资源类型是大小写敏感的,开发者能够以单数、复数和缩略的形式。例如:
kubectl get pods pod1 - name:指定资源的名称,名称也大小写敏感。如果省略名称,则会显示所有资源。例如:
kubectl get pods - flags:指定可选的参数。例如,可用-s或-server参数指定k8s api server的地址和端口。
- kubectl子命令使用分类
-
基础命令
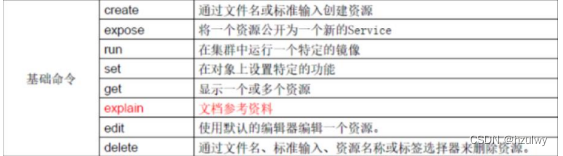
-
部署和集群管理命令
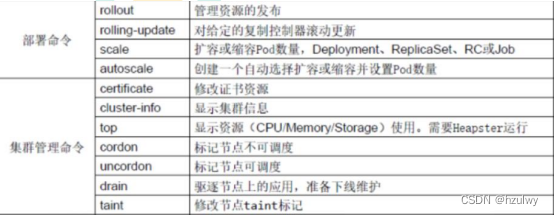
-
故障和调试命令
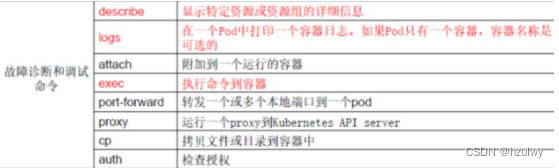
-
其他命令
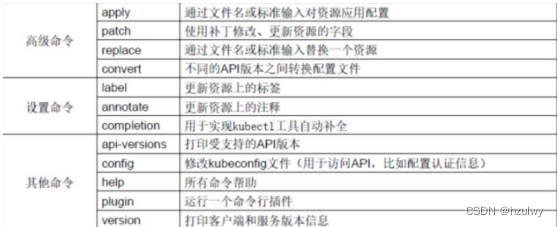
相关文章:

kubernetes集群yaml文件与kubectl工具
k8s集群中对资源管理和资源对象编排部署都可以通过声明样式(yaml)文件来解决,也就是可以把需要对资源对象操作编辑到yaml格式文件中,我们把文件叫做资源清单文件,通过kubectl命令直接使用资源清单文件就可以实现对大量的资源对象进行编排部署…...
)
python基础语法(三)
感谢各位大佬对我的支持,如果我的文章对你有用,欢迎点击以下链接 🐒🐒🐒个人主页 🥸🥸🥸C语言 🐿️🐿️🐿️C语言例题 🐣🐓🏀python 运…...
Haproxy集群与常见的Web集群调度器
文章目录 1. Web集群调度器概述1.1 Web集群调度器简介1.2 调度器类别1.2.1 常用软件类1.2.2 常用硬件类 2. Haproxy软件介绍2.1 Haproxy简介2.2 支持功能2.3 主要特性2.4 常用调度算法2.4.1 轮询:RR(Round Robin)2.4.2 最小连接数:…...

centos免密登录
centos免密登录 小白教程,一看就会,一做就成。 1.知道服务器密码的情况 ssh-keygen -t rsa #上面的命令后三次回车#然后把想要免密登录的服务器加进来 ssh-copy-id -i /root/.ssh/id_rsa.pub root192.168.10.115 #免密码登录被控的主机(ip是…...

学Python的漫画漫步进阶 -- 第十四步
学Python的漫画漫步进阶 -- 第十四步 十四、网络通信14.1 基本的网络知识14.1.1 TCP/IP14.1.2 IP地址14.1.3 端口14.1.4 HTTP/HTTPS 14.2 搭建自己的Web服务器14.3 urllib.request模块14.3.1 发送GET请求14.3.2 发送POST请求 14.4 JSON数据14.4.1 JSON文档的结构14.4.2 JSON数据…...

OpenCV(四十二):Harris角点检测
1.Harris角点介绍 什么是角点? 角点指的是两条边的交点,图中红色圈起来的点就是角点。 Harris角点检测原理:首先定义一个矩形区域,然后将这个矩形区域放置在我的图像中,求取这个区域内所有的像素值之和,之…...
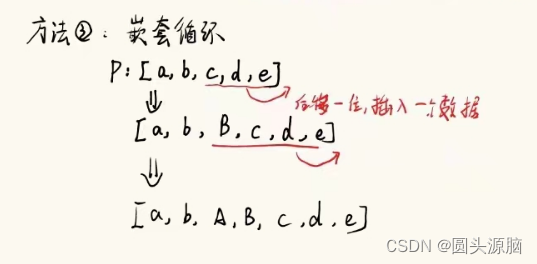
C++数据结构题:DS 顺序表--连续操作
建立顺序表的类,属性包括:数组、实际长度、最大长度(设定为 1000 ) 该类具有以下成员函数: 构造函数:实现顺序表的初始化。 插入多个数据的 multiinsert(int i, int n, int item[]) 函数,实…...

DM@命题公式@主范式的性质和应用@数理逻辑解决数字电路全加器问题
文章目录 abstract主合取范式与主析取范式间的关系👺主范式存在及唯一性定理例 主范式的性质👺求公式的成真与成假赋值主析取范式直接得到主合取范式 判断公式的类型 n n n元命题公式的主析取范式(主合取范式)的个数判断两个命题公式是否等值 给出一个满…...
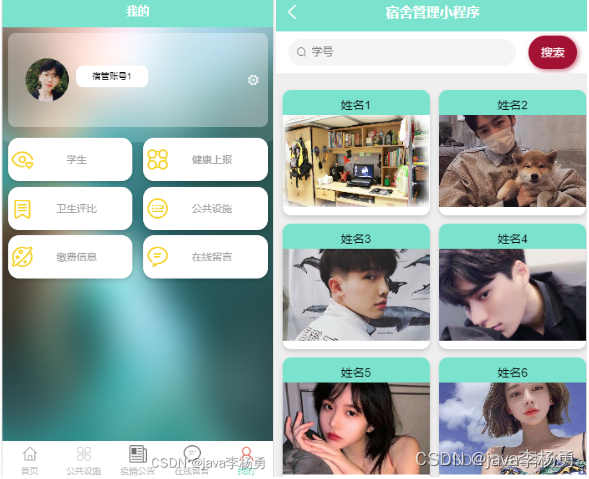
基于微信小程序+Springboot线上租房平台设计和实现【三端实现小程序+WEB响应式用户前端+后端管理】
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...
--IBERT)
Xilinx FPGA 7系列 GTX/GTH Transceivers (2)--IBERT
IBERT GTX IBERT核心提供了基础广泛的物理介质附件(PMA)评估7系列FPGA GTX收发器的演示平台。可参数化以使用不同GTX收发器和时钟拓扑,IBERT核心也可以定制使用不同的线速率、参考时钟速率和逻辑宽度。数据模式生成器和每个所需的GTX收发器都包含了检查程序,给出了几个不同…...

Python 文件介绍和正则表达式
文章目录 Python 文件和正则表达式文件打开文件读取文件直接读取 read():逐行读取采用 **for** 循环:采用 readlines(): 正则表达式匹配规则re 模块match 方法:search 方法group 方法split 方法编译:compile 方法 Pyth…...
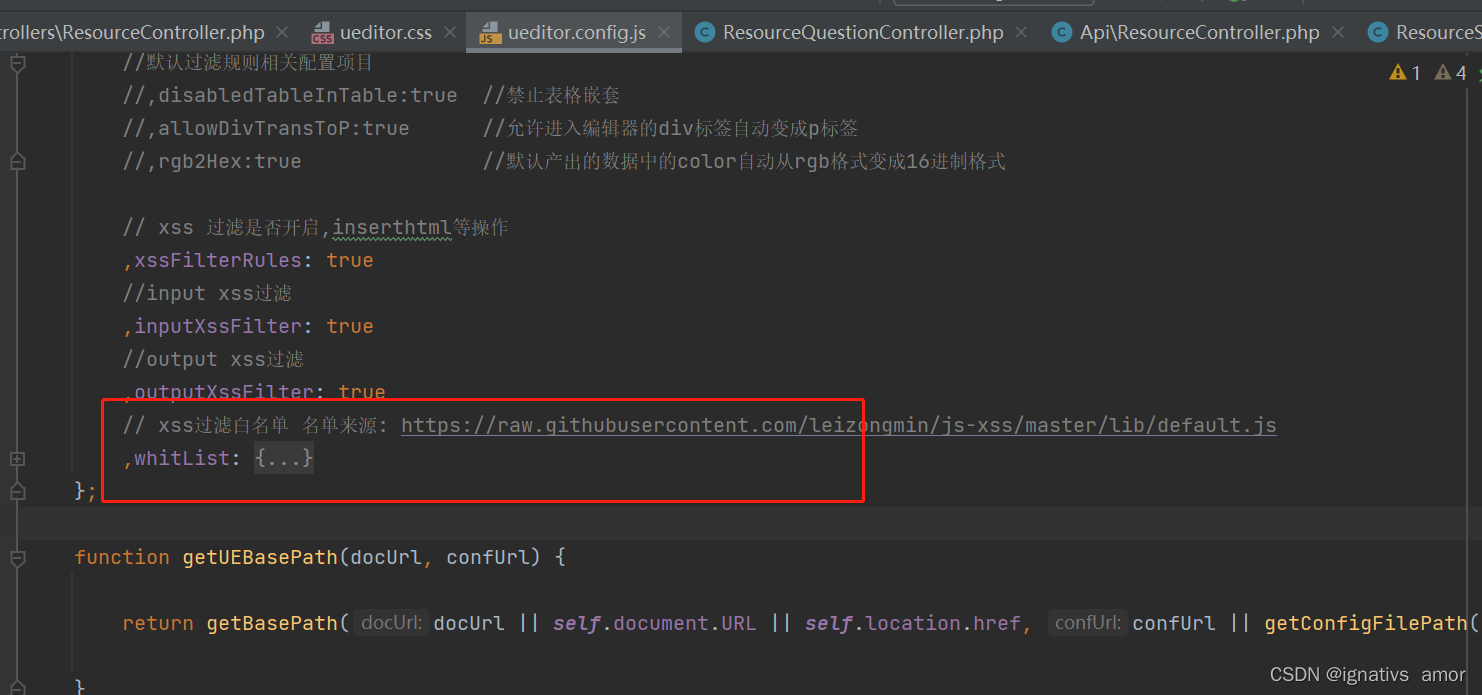
ueditor百度富文本编辑器粘贴后html丢失class和style样式
问题 项目经理从123在线编辑上排版好的文章,粘贴到项目的编辑器上,样式完全乱了, 排版是这样的: 复制到ueditor后的格式: 这天差地别呀,于是打开代码模式,发现section的属性全没了 但是,sp…...

人脸自动贴国旗
(一)简介 国庆快到了,每年这个时候,大家的头像都会贴上国旗水印,然后我就像这刚好可以用opencv dilb实现一个简单的自动将国旗贴在人脸上,刚好配合gradio写一个简单的demo gradio官方文档 (…...
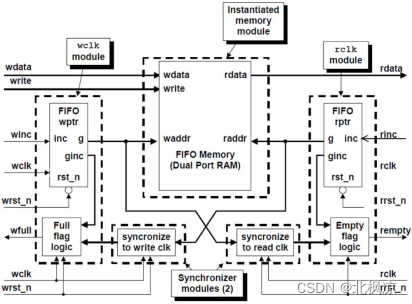
异步FIFO设计
1 FIFO简介 FIFO的本质是RAM,具有先进先出的特性。 FIFO的基本使用原则:空时不能读,满时不能写 FIFO的两个重要参数:宽度和深度 FIFO的两种类型: 同步FIFO:读写时钟相同,通常用来做数据缓存…...

学习python和anaconda的经验
PYTHON 1 常用命令 1.1 1.1 注释 Python注释多行的方法有以下三种:使用ctrl+/实现多行注释、在每一行的开头使用shift+#键、输入’‘’ ‘’或者"“” “”",将要注释的代码插在中间 1.2 def init( ):函数 区分两个函数: 1.def init(self): 这种形式在__init_…...

【Linux】多线程【上】
文章目录 前言1、Linux线程概念1-1、什么是线程?1-1-1、如何看待页表1-1-2、回顾进程地址空间1-1-3、页表怎么进行虚拟地址到物理地址的映射的?1-1-4、Linux中线程的概念(重点)1-1-5、原生线程库1-1-6、代码测试1-1-7、知识点&…...

生成式人工智能在高等教育 IT 中的作用
作者:Jared Pane 通过将你大学的数据与公共 LLMs 和 Elasticsearch 安全集成来找到你需要的答案。 根据 2023 年 4 月 EDUCAUSE 的一项调查,83% 的受访者表示,生成式人工智能将在未来三到五年内深刻改变高等教育。 学术界很快就询问和想象生…...

黑龙江省DCMM认证、CSMM认证、CMMM认证、知识产权等政策奖励
2023年8月28日 为深入落实党的二十大精神,认真落实省第十三次党代会关于创新龙江建设的部署要求,全面贯彻新发展理念,融入和服务构建新发展格局,实施创新驱动发展战略,着力建设创新龙江,不断塑造振兴发展新…...

腾讯云2023年云服务器优惠活动价格表
腾讯云经常推出各种云产品优惠活动,为了帮助大家更好地了解腾讯云服务器的价格和优惠政策,下面给大家分享腾讯云最新云服务器优惠活动价格表,助力大家轻松上云! 一、轻量应用服务器优惠活动价格表 1、轻量应用服务器:…...

Sleuth--链路追踪
1 链路追踪介绍 在大型系统的微服务化构建中,一个系统被拆分成了许多模块。这些模块负责不同的功能,组合成系统,最终可以提供丰富的功能。在这种架构中,一次请求往往需要涉及到多个服务。互联网应用构建在不同的软件模块集上&…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
