【C++】常用集合算法
0.前言

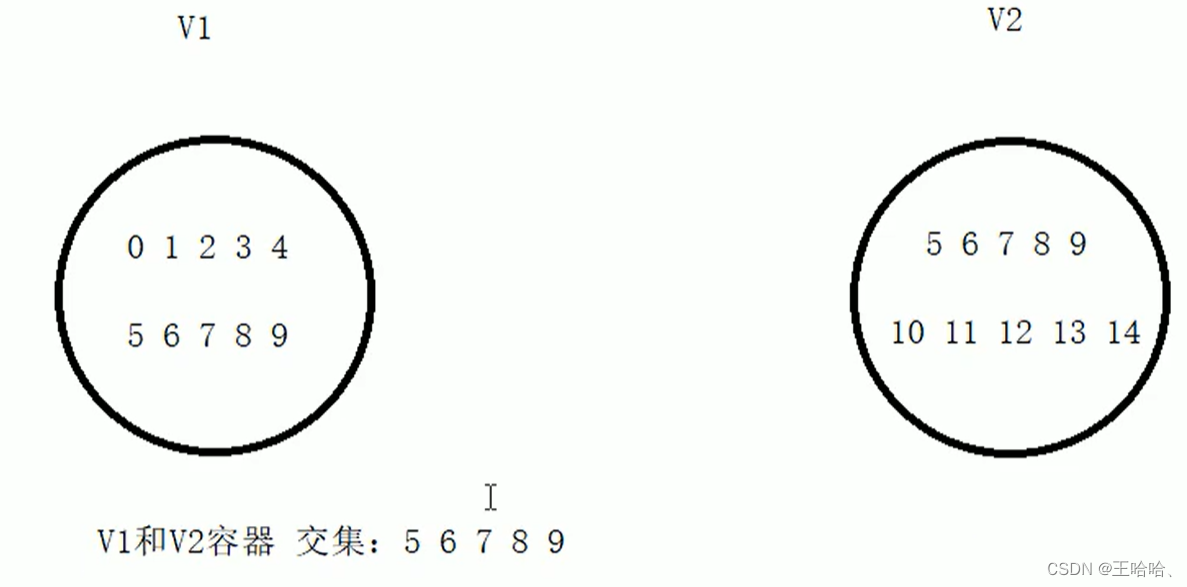
1.set_intersection

#include <iostream>
using namespace std;// 常用集合算法 交集set_intersection
#include<vector>
#include<algorithm>void myPrint(int val)
{cout << val << " ";
}void test01()
{vector<int>v1, v2;for (int i = 0; i < 10; i++){v1.push_back(i);v2.push_back(i + 5);}vector<int>TargetV;TargetV.resize(min(v1.size(), v2.size()));vector<int>::iterator Itend = set_intersection(v1.begin(), v1.end(), v2.begin(), v2.end(), TargetV.begin());for_each(TargetV.begin(), Itend, myPrint);cout << endl;
}int main()
{test01();cout << "------------------------" << endl;//test02();//cout << "------------------------" << endl << endl;//test03();//**************************************system("pause");return 0;
}

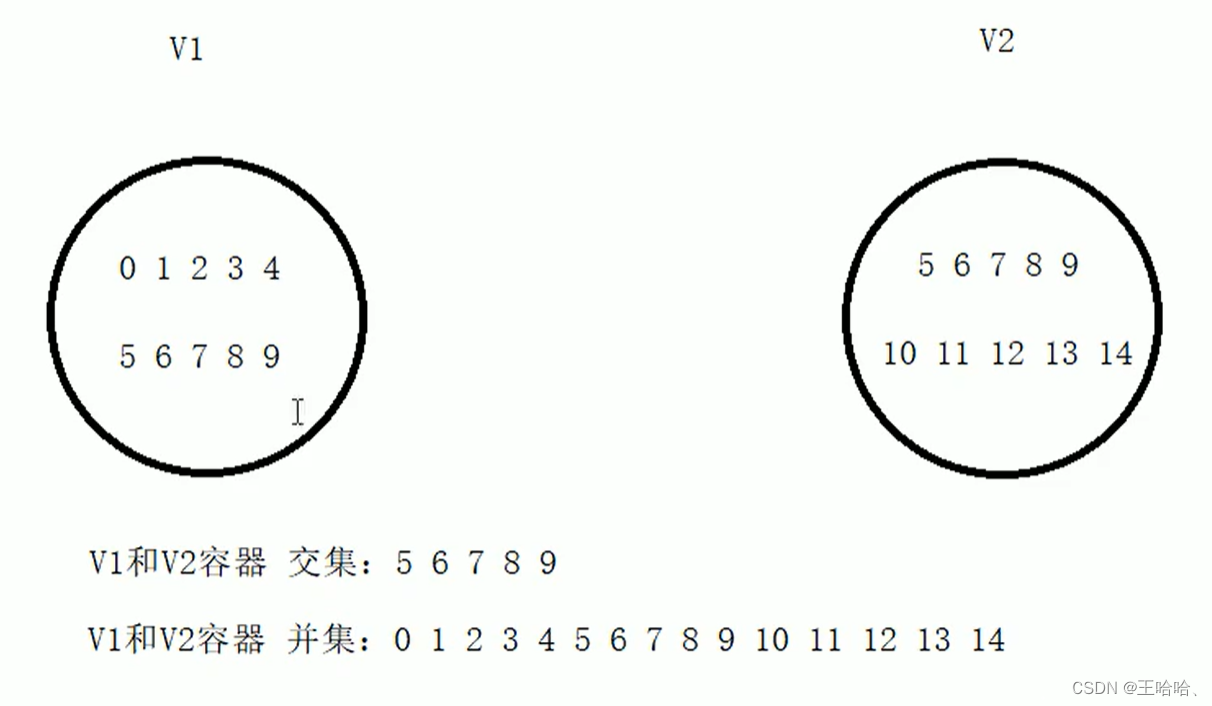
2.set_union


#include <iostream>
using namespace std;// 常用集合算法 并集set_union
#include<vector>
#include<algorithm>void myPrint(int val)
{cout << val << " ";
}void test01()
{vector<int>v1, v2;for (int i = 0; i < 10; i++){v1.push_back(i);v2.push_back(i + 5);}vector<int>TargetV;//目标容器提前开辟空间//最特殊情况 两个容器没有交集, 并集就是两个容器size相加TargetV.resize(v1.size() + v2.size());vector<int>::iterator itEnd = set_union(v1.begin(), v1.end(), v2.begin(), v2.end(), TargetV.begin());for_each(TargetV.begin(), itEnd, myPrint);cout << endl;
}int main()
{test01();cout << "------------------------" << endl;//test02();//cout << "------------------------" << endl << endl;//test03();//**************************************system("pause");return 0;
}
3.set_difference
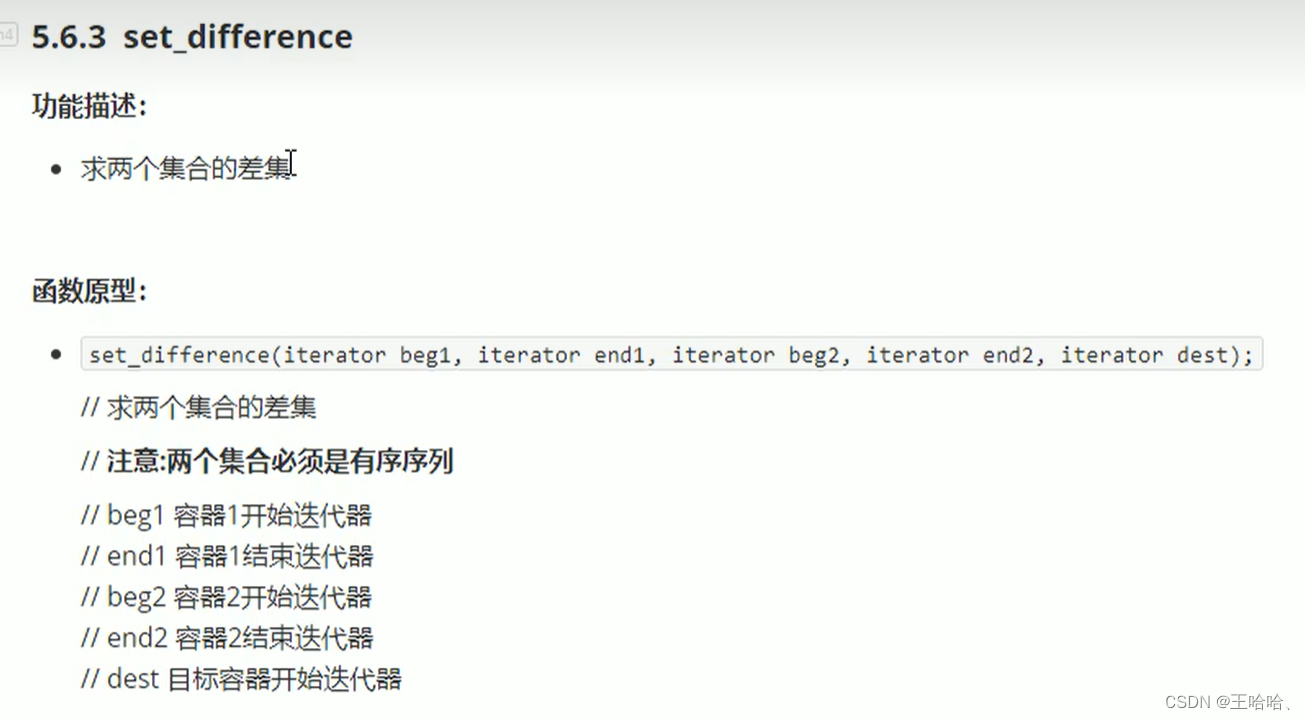


#include <iostream>
using namespace std;// 常用集合算法 差集set_difference
#include<vector>
#include<algorithm>void myPrint(int val)
{cout << val << " ";
}void test01()
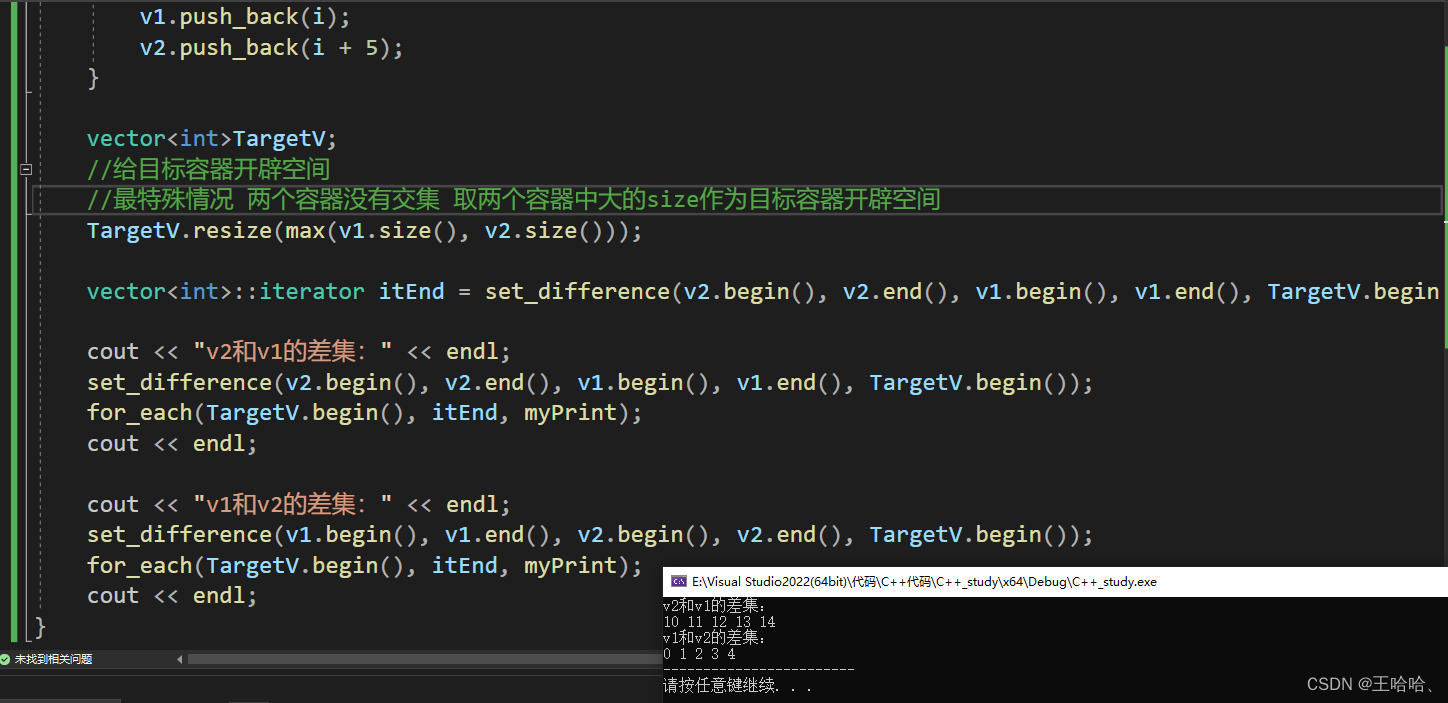
{vector<int>v1, v2;for (int i = 0; i < 10; i++){v1.push_back(i);v2.push_back(i + 5);}vector<int>TargetV;//给目标容器开辟空间//最特殊情况 两个容器没有交集 取两个容器中大的size作为目标容器开辟空间TargetV.resize(max(v1.size(), v2.size()));vector<int>::iterator itEnd = set_difference(v2.begin(), v2.end(), v1.begin(), v1.end(), TargetV.begin());cout << "v2和v1的差集:" << endl;set_difference(v2.begin(), v2.end(), v1.begin(), v1.end(), TargetV.begin());for_each(TargetV.begin(), itEnd, myPrint);cout << endl;cout << "v1和v2的差集:" << endl;set_difference(v1.begin(), v1.end(), v2.begin(), v2.end(), TargetV.begin());for_each(TargetV.begin(), itEnd, myPrint);cout << endl;
}int main()
{test01();cout << "------------------------" << endl;//test02();//cout << "------------------------" << endl << endl;//test03();//**************************************system("pause");return 0;
}
相关文章:

【C++】常用集合算法
0.前言 1.set_intersection #include <iostream> using namespace std;// 常用集合算法 交集set_intersection #include<vector> #include<algorithm>void myPrint(int val) {cout << val << " "; }void test01() {vector<int>v…...
css flex:1;详解,配合demo效果解答
前言 给设置了display:flex的子组件设置了flex:1;就能让他填满整个容器,如果有多个就平均 flex:1;是另外三个样式属性的简写,等同 flex-grow: 0; flex-shrink: 1; flex-basis: auto;我们就针…...

discuzQ安装
我们开始配置php,安装两个扩展。 在宝塔面板中,单击软件商城->已安装,查找已安装的 PHP 软件。 然后在 php 管理中,单击禁用函数,进入设置页面。 在列表中单击删除函数 putenv、readlink、symlink、shell_exec ,…...
深入解析NLP情感分析技术:从篇章到属性
目录 1. 情感分析概述1.1 什么是情感分析?- 情感分析的定义- 情感分析的应用领域 1.2 为什么情感分析如此重要?- 企业和研究的应用- 社交媒体和公共意见的影响 2. 篇章级情感分析2.1 技术概览- 文本分类的基本概念- 机器学习与深度学习方法- 词嵌入的力量…...
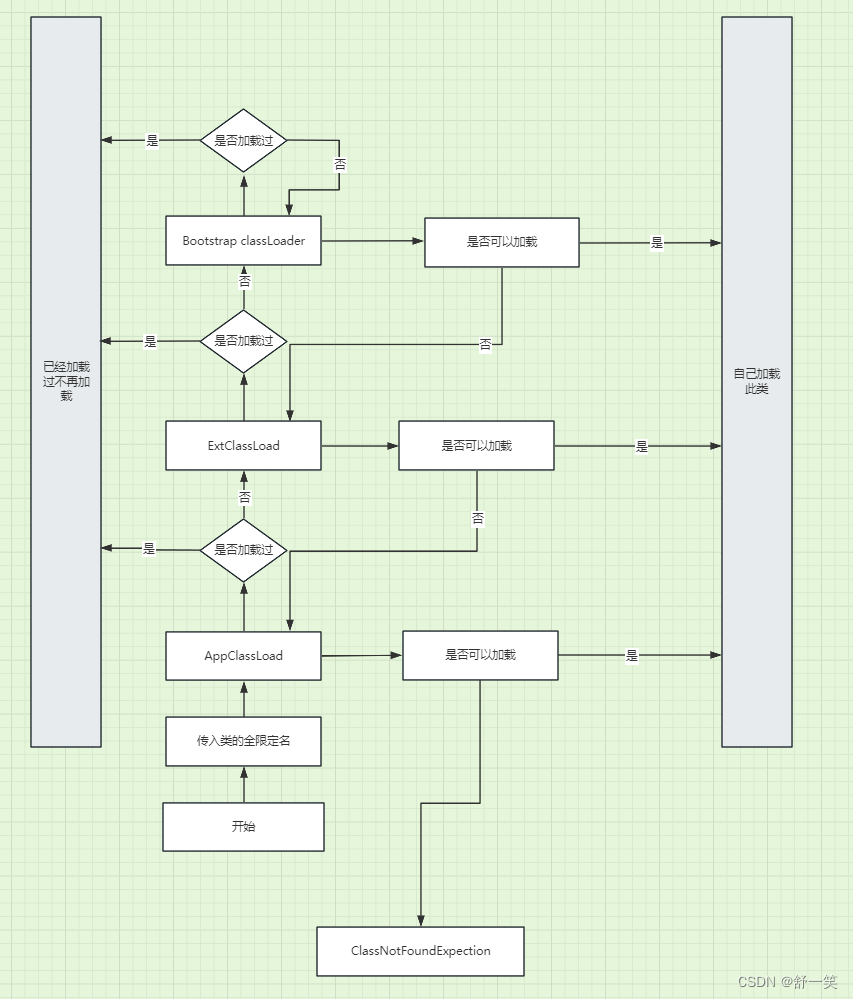
JVM的双亲委派模型
定义与本质: 类加载器用来把类文件加载到JVM内存中。从JDK1.2开始,类加载过程采用双亲委派模型,保证Java平台安全。 父类委托的定义: 一个类加载器在接到加载类请求的时候,首先不会去加载这个类,而是把这个…...

js中如何判断一个变量是否为数字类型?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐使用Number.isNaN()方法⭐使用正则表达式⭐使用isNaN()函数⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个…...
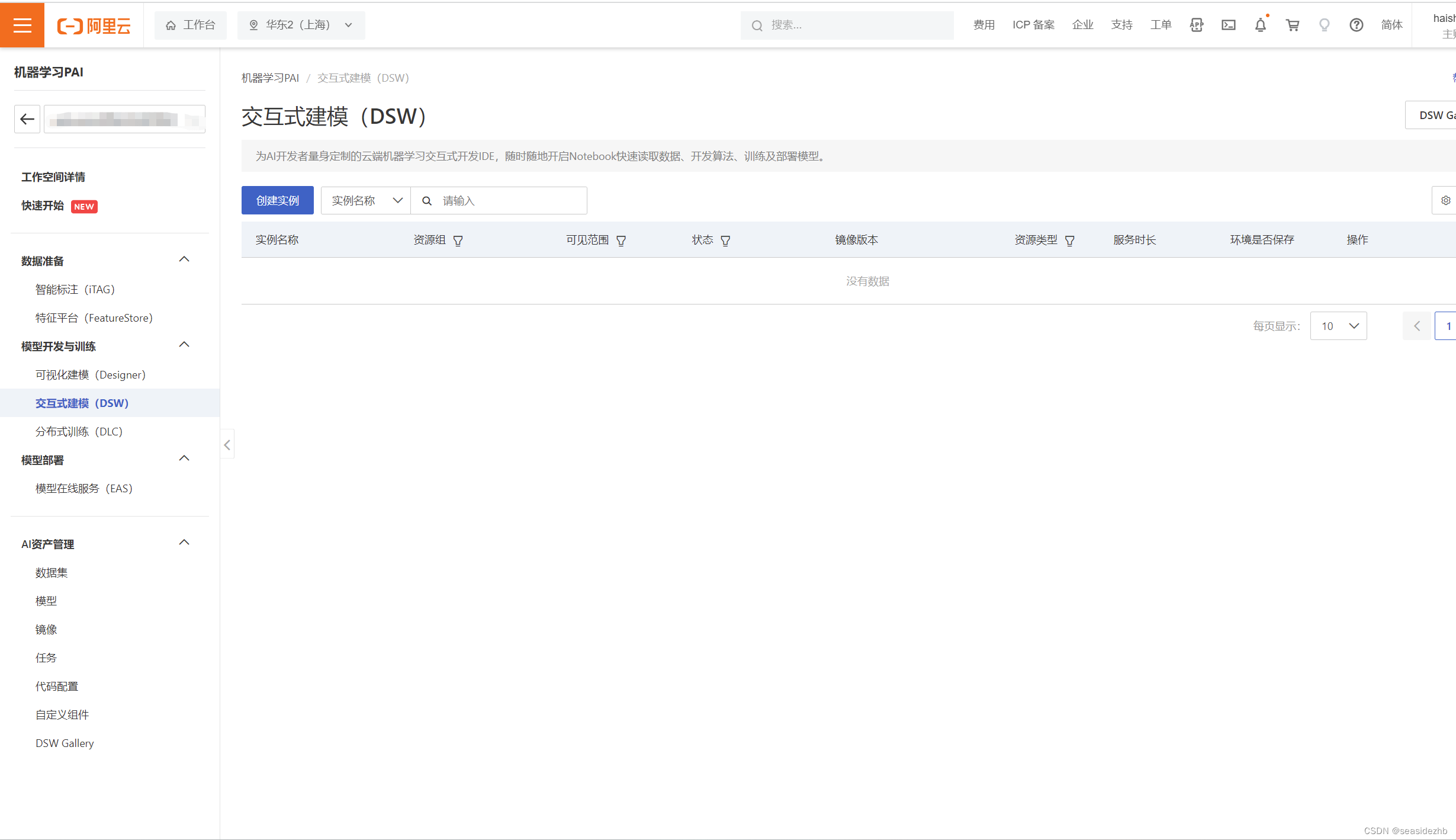
使用阿里PAI DSW部署Stable Diffusion WebUI
进入到网址https://pai.console.aliyun.com/里边。 点击创建实例。 把实例名称填写好,选择GPU规格,然后选择实例名称是ecs.gn6v-c8g1.2xlarge。 选择stable-diffusion-webui-env:pytorch1.13-gpu-py310-cu117-ubuntu22.04,然后点击下一步。…...

redisson使用过程常见问题汇总
文章目录 常见报错1. 配置方式使用错误2. 版本差异报错3. 配置文件中配置了密码或者配置错误4. 字符集和序列化方式配置问题5. Redisson的序列化问题6. 连接池问题:7. Redisson的高可用性问题:8. Redisson的并发问题9. Redisson的性能问题 2. 参考文档 常…...

代码随想录训练营 DP序列
代码随想录训练营 DP序列 718. 最长重复子数组🌸code 674. 最长连续递增序列🌸code 300.最长递增子序列🌸code 最后一题很巧妙,不能单纯的去把DP当作板子题,得思考才能得到最佳方式 718. 最长重复子数组🌸 …...

Datastage部署与使用
Datastage部署与使用 - 码农教程 https://www.cnblogs.com/lanston/category/739553.html Streamsets定时拉取接口数据同步到HBase集群_streamsets api_webmote的博客-CSDN博客 【SDC】StreamSets实战之路-28-实战篇- 使用StreamSets实时采集指定数据目录文件并写入库Kudu_菜…...

【实用工具】Centos 安装ARL灯塔
文章目录 docker 安装安装docker-compose配置镜像加速器ARL安装和启动 docker 安装 yum install https://download.docker.com/linux/fedora/30/x86_64/stable/Packages/containerd.io-1.2.6-3.3.fc30.x86_64.rpm yum install docker-ce (若出现无法找到包可能是镜像源问题) 更…...

IP地址定位基础数据采集
在互联网时代,IP地址定位技术已经成为了广泛应用的一项重要技术。无论是用于网络安全、广告投放、市场调研还是用户体验优化,IP地址定位技术都发挥着关键作用。 什么是IP地址定位? IP地址定位是一种技术,它通过IP地址来确定设备…...

leetcode做题笔记138. 复制带随机指针的链表
给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。 构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 n…...

分布式文件系统的新兴力量:揭秘Alluxio的元数据管理机制【文末送书】
文章目录 写在前面01 分布式文件系统元数据的常见类型1.1 文件(inode)元数据1.2 数据块(block)元数据1.3 Worker元数据 02 分布式文件系统元数据的存储模式2.1 元数据存储在堆上(HEAP模式)2.2 元数据存储在…...
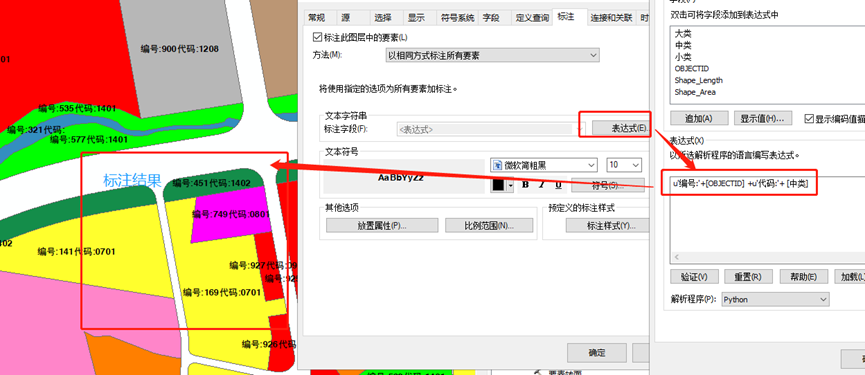
ArcGIS标注的各种用法和示例
标注是将描述性文本放置在地图中的要素上或要素旁的过程。 本文整理了ArcGIS中的各种标注方法、可能遇到的问题和细节,内容比较杂,想到哪写到哪。 一、正常标注某一字段值的内容 右键点击【属性】,在【标注】选项卡下勾选【标注此图层中的的要素】,在【文本字符串】栏中…...

修改ros中的控制器,便于仿真和驱动真实UR
UR机械臂学习(5-3):驱动ur机械臂实物——问题及解决_error: 鈥榰r_msgs::setpayloadrequest {aka struct ur__冰激凌啊的博客-程序员宝宝 - 程序员宝宝 (cxybb.com) 问题5 Action client not connected: scaled_pos_traj_controller/follow_j…...

网络广播模块2*30W 智能4G广播终端开发模块
SV-704UG 4G网络广播模块2*30W 智能4G广播终端开发模块 一、描述 SV-704UG网络音频模块是一款带2*30W功放输出的4G广播音频模块,采用高性能ARM处理器及专业Codec,能接收4G广播音频数据流,转换成音频模拟信号输出。带有一路line in输入&#…...

优思学院|什么是精益项目管理?
正确地使用精益思想和技术是可以减少项目中的浪费、提高客户满意度,并提高项目的利润率。 在现实世界中,项目经理的工作充满了挑战。他们不仅需要专注于产品和团队,还必须确保客户的满意度。同时,他们还必须与矩阵组织打交道&…...
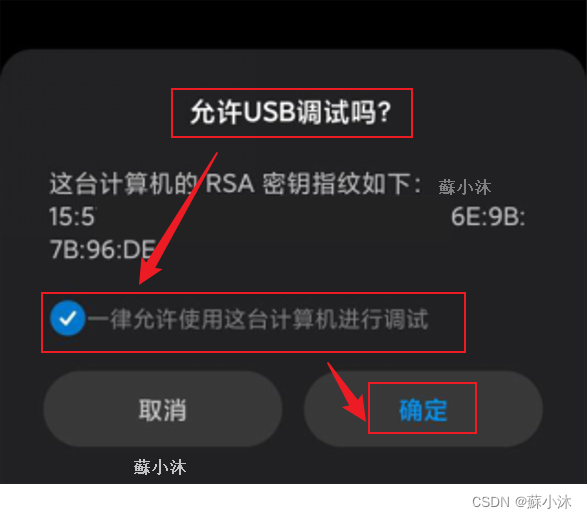
【Android取证篇】华为设备跳出“允许USB调试“界面方法的不同方法
【Android取证篇】华为设备跳出"允许USB调试"界面方法的不同方法 华为设备在鸿蒙OS3系统之后,部分设备启用"允许USB调试"方式会有所变化,再次做个记录—【蘇小沐】 1.实验环境 系统版本Windows 11 专业工作站版22H2(2…...
在VSCode中移除不必要的扩展
在VSCode中移除不必要的扩展 在VSCode中安装扩展是编辑器缓慢且耗电的主要原因之一,因为添加的每个新扩展都会增加应用程序的内存和 CPU 使用率。 VSCode现在已经具备了非常多的功能,我们可以将一些重复工作的扩展移除掉。卸载这些现在可有可无的扩展将…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

【Ftrace 专栏】Ftrace 参考博文
ftrace、perf、bcc、bpftrace、ply、simple_perf的使用Ftrace 基本用法Linux 利用 ftrace 分析内核调用如何利用ftrace精确跟踪特定进程调度信息使用 ftrace 进行追踪延迟Linux-培训笔记-ftracehttps://www.kernel.org/doc/html/v4.18/trace/events.htmlhttps://blog.csdn.net/…...

新版NANO下载烧录过程
一、序言 搭建 Jetson 系列产品烧录系统的环境需要在电脑主机上安装 Ubuntu 系统。此处使用 18.04 LTS。 二、环境搭建 1、安装库 $ sudo apt-get install qemu-user-static$ sudo apt-get install python 搭建环境的过程需要这个应用库来将某些 NVIDIA 软件组件安装到 Je…...
