每日一题 1601最多可达成的换楼请求数目(子集模版)
题目
1601
我们有 n 栋楼,编号从 0 到 n - 1 。每栋楼有若干员工。由于现在是换楼的季节,部分员工想要换一栋楼居住。
给你一个数组 requests ,其中 requests[i] = [fromi, toi] ,表示一个员工请求从编号为 fromi 的楼搬到编号为 toi 的楼。
一开始 所有楼都是满的,所以从请求列表中选出的若干个请求是可行的需要满足 每栋楼员工净变化为 0 。意思是每栋楼 离开 的员工数目 等于 该楼 搬入 的员工数数目。比方说 n = 3 且两个员工要离开楼 0 ,一个员工要离开楼 1 ,一个员工要离开楼 2 ,如果该请求列表可行,应该要有两个员工搬入楼 0 ,一个员工搬入楼 1 ,一个员工搬入楼 2 。
请你从原请求列表中选出若干个请求,使得它们是一个可行的请求列表,并返回所有可行列表中最大请求数目。
示例 1:
输入:n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
输出:5
解释:请求列表如下:
从楼 0 离开的员工为 x 和 y ,且他们都想要搬到楼 1 。
从楼 1 离开的员工为 a 和 b ,且他们分别想要搬到楼 2 和 0 。
从楼 2 离开的员工为 z ,且他想要搬到楼 0 。
从楼 3 离开的员工为 c ,且他想要搬到楼 4 。
没有员工从楼 4 离开。
我们可以让 x 和 b 交换他们的楼,以满足他们的请求。
我们可以让 y,a 和 z 三人在三栋楼间交换位置,满足他们的要求。
所以最多可以满足 5 个请求。
示例 2:
输入:n = 3, requests = [[0,0],[1,2],[2,1]]
输出:3
解释:请求列表如下:
从楼 0 离开的员工为 x ,且他想要回到原来的楼 0 。
从楼 1 离开的员工为 y ,且他想要搬到楼 2 。
从楼 2 离开的员工为 z ,且他想要搬到楼 1 。
我们可以满足所有的请求。
示例 3:
输入:n = 4, requests = [[0,3],[3,1],[1,2],[2,0]]
输出:4
题解
class Solution {private int max = 0;private int[][] requests;private int[] buildings;private int cnt = 0;public int maximumRequests(int n, int[][] requests) {buildings = new int[n];this.requests = requests;dfs(0);return max;}private void dfs(int i) {if (check()) {max = Math.max(cnt,max);}if (i == requests.length) {return;}for (int j = i; j < requests.length; j++) {buildings[requests[j][0]]--;buildings[requests[j][1]]++;cnt++;dfs(j+1);//返回操作buildings[requests[j][0]]++;buildings[requests[j][1]]--;cnt--;}}//判断是否分配合理private boolean check() {for (int i : buildings) {if (i != 0) {return false;}}return true;}
}
相关文章:
)
每日一题 1601最多可达成的换楼请求数目(子集模版)
题目 1601 我们有 n 栋楼,编号从 0 到 n - 1 。每栋楼有若干员工。由于现在是换楼的季节,部分员工想要换一栋楼居住。 给你一个数组 requests ,其中 requests[i] [fromi, toi] ,表示一个员工请求从编号为 fromi 的楼搬到编号为…...
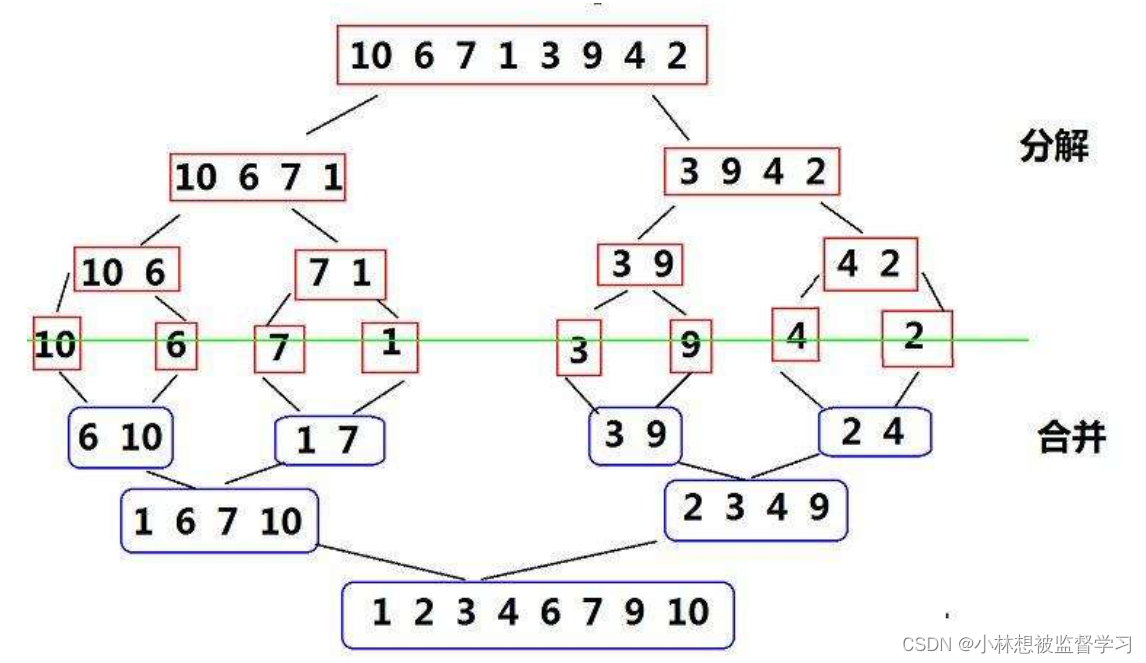
排序算法-归并排序
属性 归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序&#…...

vue3 整合 springboot 打完整jar包
前端 .env.developmen VITE_APP_BASE_URL/api.env.production VITE_APP_BASE_URL/axios 配置 axios.defaults.baseURL import.meta.env.VITE_APP_BASE_URLpackage.json "scripts": {"dev": "vite --mode development","build": &…...

依赖倒转原则是什么?
依赖倒转原则(Dependency Inversion Principle)是面向对象设计中的另一个基本原则,它是由Robert C. Martin提出的,它的中心思想是面向接口编程,该原则指出高层模块不应该依赖于低层模块,两者都应该依赖于抽…...

什么是GPT与MBR
GPT(GUID Partition Table)和MBR(Master Boot Record)是两种不同的磁盘分区表格式。 MBR是一种较早的磁盘分区表格式,它使用512字节的扇区作为存储空间。MBR分区表可以定义最多4个主分区,每个主分区都可以…...

前后端开发接口联调对接参数
前言 一个完整的互联网系统项目,需要前后端配合,进行上线,针对前端开发者,现在互联网主流的项目都是前后端分离 也就是后端负责提供数据接口,前端负责UI界面数据渲染 凡是在前台数据展示与用户交互的,都是由前端来实现的,而数据来源是由后台服务提供的 在浏览器c端能够发送后端…...

定时任务框架-xxljob
1.定时任务 spring传统的定时任务Scheduled,但是这样存在这一些问题 : 做集群任务的重复执行问题 cron表达式定义在代码之中,修改不方便 定时任务失败了,无法重试也没有统计 如果任务量过大,不能有效的分片执行 …...
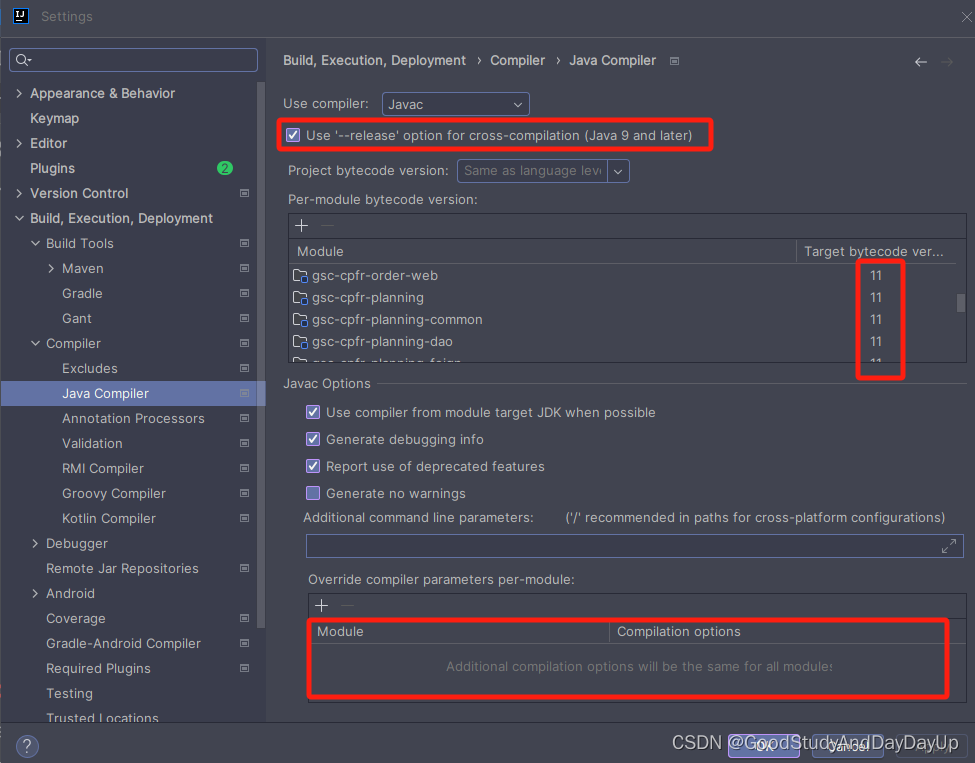
idea项目配置三大步
场景: 使用 idea 打开一个新项目的时候,想让项目迅速跑起来, 其实只需要下面简单三步: 1. 首先,配maven 2. 其次,配置 jdk 这里配置 project 就行了,不用管Modules中的配置。 3. 最后&#…...

学会SpringMVC之自定义注解各种场景应用,提高开发效率及代码质量
目录 一、简介 ( 1 ) 是什么 ( 2 ) 分类 ( 3 ) 作用 二、自定义注解 ( 1 ) 如何自定义注解 ( 2 ) 场景演示 场景一(获取类与方法上的注解值) 场景二( 获取类属性上的注解属性值 ) 场景三( 获取参数修…...
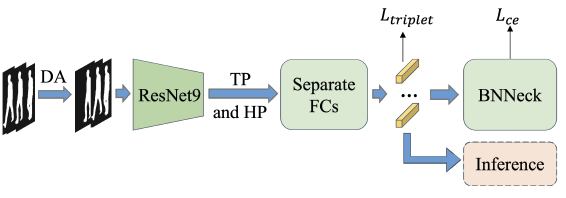
步态识别常见模块解读及代码实现:基于OpenGait框架
步态识别常见模块解读及代码实现:基于OpenGait框架 最近在看步态识别相关论文,但是因为记忆力下降的原因,老是忘记一些内容。因此记录下来方便以后查阅,仅供自己学习参考,没有背景知识和论文介绍。 目录 步态识别常见…...

前端八股文之“闭包”
一、定义 一句话概括闭包:能够访问函数内部变量的函数与这个变量的组合构成了闭包结构。如下代码 function fuc1(){let num 999return function fuc2(){console.log(num)}}fuc1()(); 如代码所示,fuc2和父级变量num构成了一个闭包环境。 二、原理 子…...

数据可视化:掌握数据领域的万金油技能
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据开发、数据分析等。 🐴欢迎小伙伴们点赞👍🏻、收藏⭐️、…...
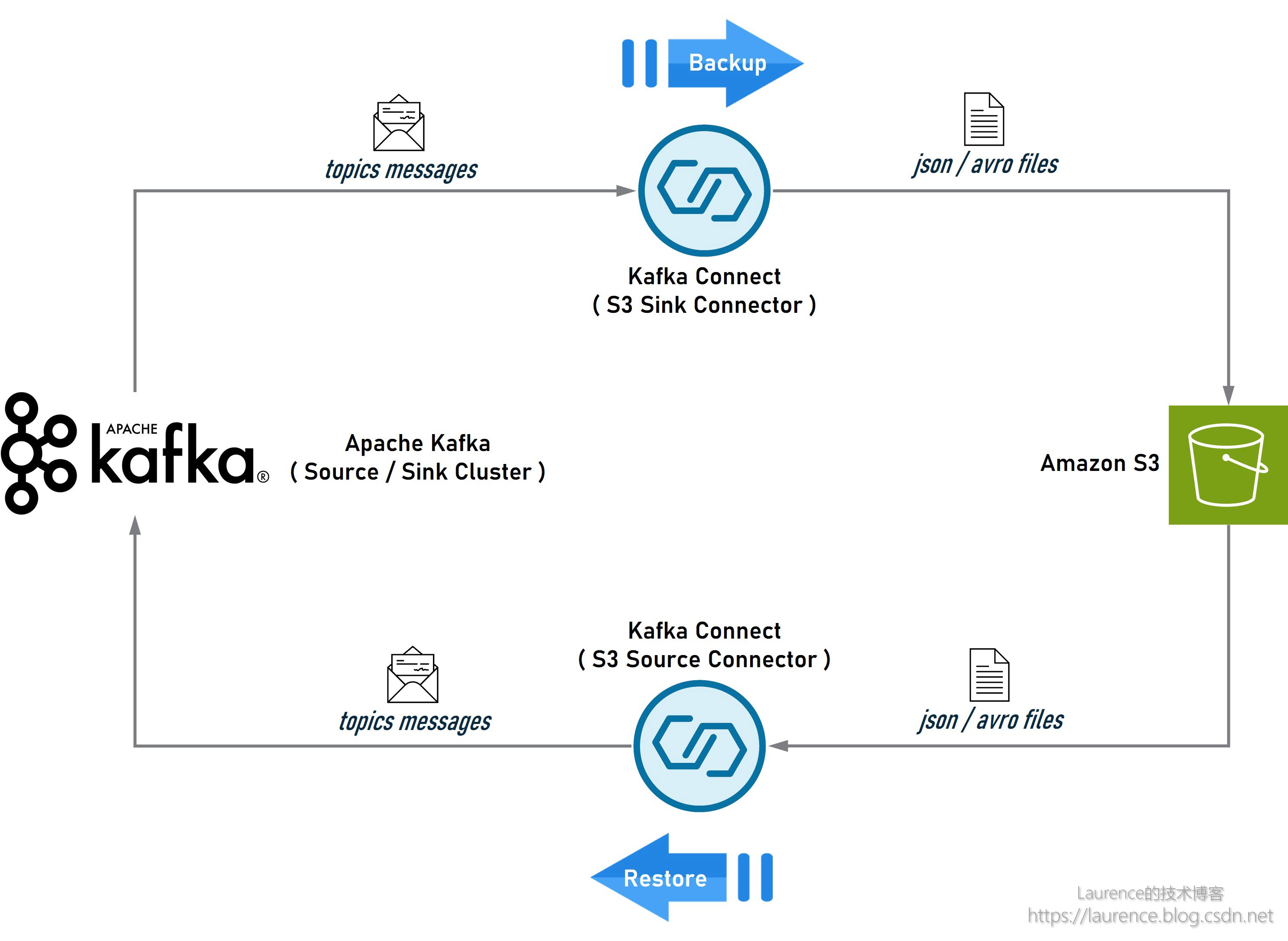
Apache Kafka 基于 S3 的数据导出、导入、备份、还原、迁移方案
在系统升级或迁移时,用户常常需要将一个 Kafka 集群中的数据导出(备份),然后在新集群或另一个集群中再将数据导入(还原)。通常,Kafka集群间的数据复制和同步多采用 Kafka MirrorMaker࿰…...

事务管理AOP
事务管理 事务回顾 概念:事务是一组操作的集合,它是一个不可分割的工作单位,这些操作要么同时成功,要么同时失败 操作: 开启事务:一组操作开始前,开启事务-start transaction/be…...

Java从Tif中抽取最大的那张图进行裁剪成x*y份
之前我有一篇帖子《kfb格式文件转jpg格式》讲述到 kfb > tif > jpg,但是针对于超大tif中的大图是无法顺利提取的,就算是能顺利提取,试想一下,2G的tif文件,如果能提取处理最大的那张图,并且在不压缩的…...

人工智能AI界的龙头企业,炸裂的“英伟达”时代能走多远
原创 | 文 BFT机器人 1、AI芯片的竞争格局已趋白热化 尽管各类具有不同功能和定位的AI芯片在一定程度上可实现互补,但同时也在机遇与挑战并存中持续调整定位。在AI训练端,英伟达的GPU凭着高算力的门槛,一直都是训练端的首选。 只有少数芯片能…...

【实战】H5 页面同时适配 PC 移动端 —— 旋转横屏
文章目录 一、场景二、方案三、书单推荐01 《深入实践Kotlin元编程》02 《Spring Boot学习指南》03 《Kotlin编程实战》 一、场景 一个做数据监控的单页面,页面主要内容是一个整体必须是宽屏才能正常展示,这时就不能用传统的适配方案了,需要…...
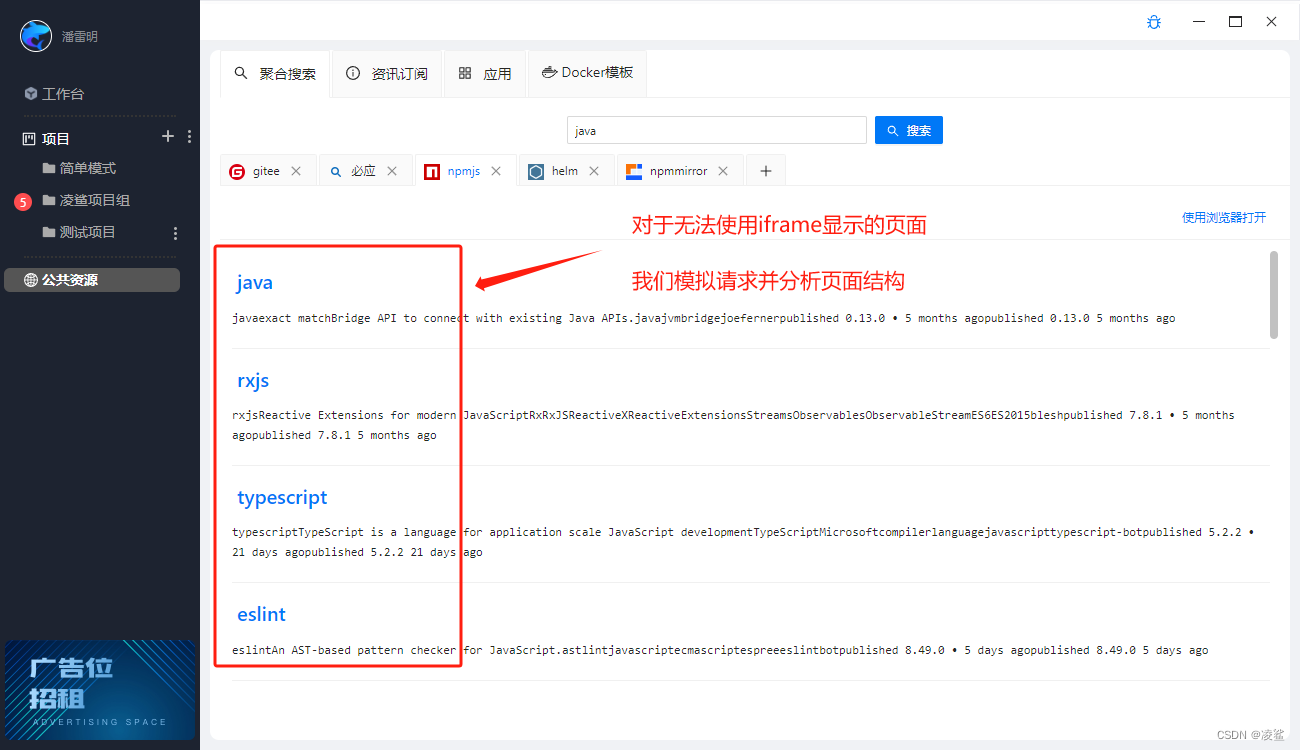
使用凌鲨进行聚合搜索
作为研发人员,我们经常需要在多个来源之间查找信息,以便进行研发工作。除了常用的搜索引擎如百度和必应之外,我们还需要查阅各种代码文档和依赖包等资源。这些资源通常分散在各个网站和文档库中,需要花费一定的时间和精力才能找到…...

程序设计之——手把手教你如何从Excel文件中读取学生信息
在当今信息化时代,计算机技术已经深入到各个领域,而程序设计则成为推动信息化建设的关键技术之一。在众多领域中,学生信息管理系统无疑是其中一个重要的应用。本文将从学生信息管理系统的开发入手,探讨开如何高效且保证质量的完成…...

Docker容器化技术(从零学会Docker)
文章目录 前言一、初识Docker1.初识Docker-Docker概述2.初识Docker-安装Docker3.初识Docker-Docker架构4.初识Docker-配置镜像加速器 二、Docker命令1.Docker命令-服务相关命令2.Docker命令-镜像相关命令3.Docker命令-容器相关命令 三、Docker容器的数据卷1.Docker容器数据卷-数…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

MyBatis中关于缓存的理解
MyBatis缓存 MyBatis系统当中默认定义两级缓存:一级缓存、二级缓存 默认情况下,只有一级缓存开启(sqlSession级别的缓存)二级缓存需要手动开启配置,需要局域namespace级别的缓存 一级缓存(本地缓存&#…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...
