徐亦达机器学习:Kalman Filter 卡尔曼滤波笔记 (一)

P ( x t P(x_t P(xt| x t − 1 ) x_{t-1}) xt−1) | P ( y t P(y_t P(yt| x t ) x_t) xt) | P ( x 1 ) P(x_1) P(x1) | |
|---|---|---|---|
| Discrete State DM | A X t − 1 , X t A_{X_{t-1},X_t} AXt−1,Xt | Any | π \pi π |
| Linear Gassian Kalman DM | N ( A X t − 1 + B , Q ) N(AX_{t-1}+B,Q) N(AXt−1+B,Q) | N ( H X t + C , R ) N(HX_t+C,R) N(HXt+C,R) | N ( μ 0 , ϵ 0 ) N(\mu_0,\epsilon_0) N(μ0,ϵ0) |
| No-Linear NoGaussian DM | f ( x t − 1 ) f(x_{t-1}) f(xt−1) | g ( y t ) g(y_t) g(yt) | f ( x 1 ) f(x_1) f(x1) |
{ P ( y 1 , . . . , y t ) − − e v a l u a t i o n a r g m e n t θ log P ( y 1 , . . . , y t ∣ θ ) − − p a r a m e t e r l e a r n i n g P ( x 1 , . . . , x t ∣ y 1 , . . . , y t ) − s t a t e d e c o d i n g P ( x t ∣ y 1 , . . , y t ) − f i l t e r i n g \left\{ \begin{aligned} P(y_1,...,y_t)--evaluation\\ argment \theta \log{P(y1,...,y_t|\theta)}--parameter learning \\ P(x_1,...,x_t|y_1,...,y_t)-state decoding \\ P(x_t | y_1,..,y_t)-filtering \end{aligned} \right. ⎩ ⎨ ⎧P(y1,...,yt)−−evaluationargmentθlogP(y1,...,yt∣θ)−−parameterlearningP(x1,...,xt∣y1,...,yt)−statedecodingP(xt∣y1,..,yt)−filtering
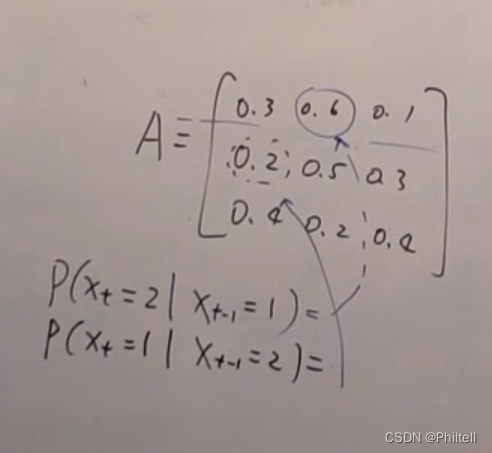
线性高斯噪声的动态模型
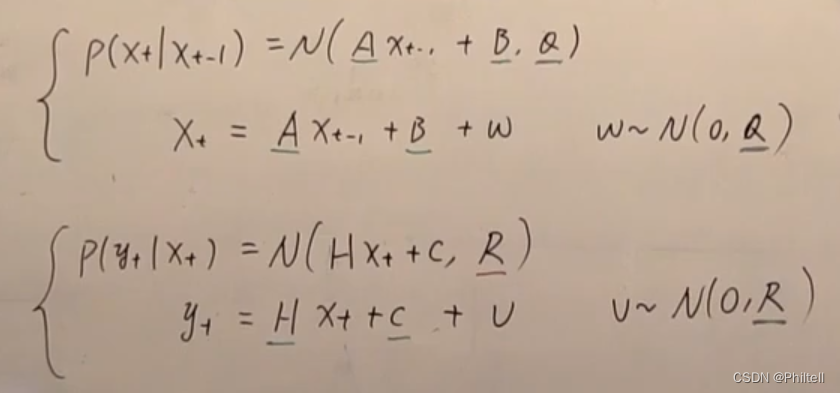
P ( x t ∣ y 1 , . . . , y t ) P(x_t|y_1,...,y_t) P(xt∣y1,...,yt)
假设转移概率是 P ( x t ∣ X t − 1 ) = N ( A X t − 1 + B , Q ) P(x_t|X_{t-1})= N(AX_{t-1}+B,Q) P(xt∣Xt−1)=N(AXt−1+B,Q)
X t = A X t − 1 + B + ω X_t = AX_{t-1}+B+\omega Xt=AXt−1+B+ω , ω ∼ N ( 0 , Q ) \omega \sim N(0,Q) ω∼N(0,Q)
measurement probility
P ( y t ∣ x t ) = N ( H X t + C , R ) P(y_t|x_t) = N(HX_t+C,R) P(yt∣xt)=N(HXt+C,R)
y t = H X t + C + v y_t = HX_t+C+v yt=HXt+C+v
v ∼ N ( 0 , R ) v \sim N(0,R) v∼N(0,R)
以下都是参数。
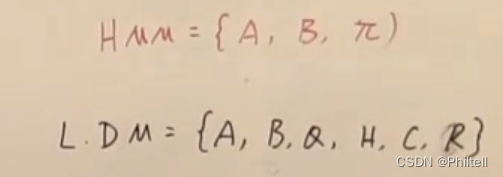
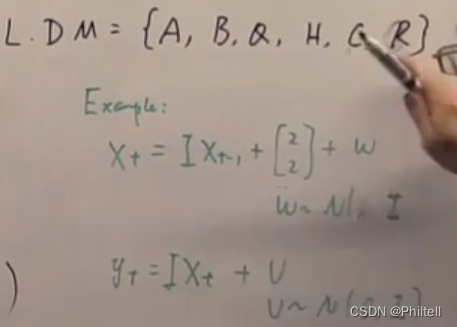


filter公式推导


HMM模型,当隐变量确定的时候,观测就变成独立的了。

- 卡尔曼滤波,当t = 1的时候,我们就知道 P ( x 1 ∣ y 1 ) ∼ N ( u ^ 1 , σ ^ 1 ) P(x_1|y_1) \sim N(\hat u_1,\hat \sigma_1) P(x1∣y1)∼N(u^1,σ^1)
- t = 2的时候, P ( x 2 ∣ y 2 ) ∼ N ( u ‾ 2 , σ ‾ 2 ) P(x_2|y_2) \sim N(\overline u_2,\overline \sigma_2) P(x2∣y2)∼N(u2,σ2)

个人理解
- 卡尔曼滤波可以理解为滤波器的一种,用数学表达就是用观测量 y 1 , y 2 , y 3 . . . , y t y_1,y_2,y_3...,y_t y1,y2,y3...,yt来获得t时刻的估计量 x t x_t xt,数学公式为
P ( x t ∣ y 1 , . . . , y t ) P(x_t|y_1,...,y_t) P(xt∣y1,...,yt)正比与 P ( x t , y 1 , . . . , y t ) P(x_t,y_1,...,y_t) P(xt,y1,...,yt)可以理解为前置条件 y 1 , . . . , y t y_1,...,y_t y1,...,yt发生的条件下有发生 x t x_t xt的概率与两类事件同时发生的概率是成正比的。可以简单理解为 P ( A ∣ B ) P(A|B) P(A∣B)与 P ( A , B ) P(A,B) P(A,B)成正比。 - 那么得出 P ( x t ∣ y 1 , . . . , y t ) ∝ P ( x t , y 1 , . . . , y t ) ∝ P ( y t ∣ x t , y 1 , . . . , y t − 1 ) ∗ P ( x t ∣ y 1 , . . . , y t − 1 ) P(x_t|y_1,...,y_t) \propto P(x_t,y_1,...,y_t) \propto P(y_t|x_t,y_1,...,y_{t-1}) * P(x_t|y_1,...,y_{t-1}) P(xt∣y1,...,yt)∝P(xt,y1,...,yt)∝P(yt∣xt,y1,...,yt−1)∗P(xt∣y1,...,yt−1)
- 有HMM可以得知, P ( y t ) P(y_t) P(yt)发生的概率是只跟 x t x_t xt相关,因此 P ( y t ∣ x t , y 1 , . . . , y t − 1 ) = P ( y t ∣ x t ) P(y_t|x_t,y_1,...,y_t-1) = P(y_t|x_t) P(yt∣xt,y1,...,yt−1)=P(yt∣xt),而 x t x_t xt的估计量,是通过上一次观测获得, x t x_t xt与 y 1 , . . . , y t − 1 y_1,...,y_{t-1} y1,...,yt−1相关。
- 那么得出预测为 P ( x t ∣ y 1 , . . . , y t − 1 ) P(x_t|y_1,...,y_{t-1}) P(xt∣y1,...,yt−1),前t-1时刻的观测值估计下一刻t的状态。
- 将 x t x_t xt看为常量,将 x t − 1 x_{t-1} xt−1看为变量,那么就得到了预测公式的推导公式为 P ( x t ∣ y 1 , . . . , y t − 1 ) = ∫ d ( x t − 1 ) P ( x t , x t − 1 ∣ y 1 , . . . , y t ) d x t − 1 ∝ ∫ x t − 1 P ( x t ∣ x t − 1 ) P ( x t − 1 ∣ y 1 , . . . , y t − 1 ) d ( x t − 1 ) P(x_t|y_1,...,y_{t-1})=\int_{d(x_{t-1})}{P(x_t,x_{t-1}|y_1,...,y_t)dx_{t-1}} \propto \int_{x_{t-1}}P(x_t|x_{t-1})P(x_{t-1}|y_1,...,y_{t-1})d(x_{t-1}) P(xt∣y1,...,yt−1)=∫d(xt−1)P(xt,xt−1∣y1,...,yt)dxt−1∝∫xt−1P(xt∣xt−1)P(xt−1∣y1,...,yt−1)d(xt−1)

总结
- 预测:不知道当前时刻的观测,用上一时刻观测与预测当前时刻的状态
P ( x t ∣ y 1 , . . . , y t − 1 ) = ∫ P ( x t ∣ x t − 1 ) P ( x t − 1 ∣ y 1 , . . . , y t − 1 ) P(x_t|y_1,...,y_{t-1})= \int P(x_t|x_{t-1})P(x_{t-1}|y_1,...,y_{t-1}) P(xt∣y1,...,yt−1)=∫P(xt∣xt−1)P(xt−1∣y1,...,yt−1) - 更新:已经知道当前时刻的观测,用当前的观测更新当前可是的状态
P ( x t ∣ y 1 , . . . , y t ) = P ( y t ∣ x t ) P ( x t ∣ y 1 , . . . , y t − 1 ) P(x_t|y_1,...,y_t)=P(y_t|x_t)P(x_t|y_1,...,y_{t-1}) P(xt∣y1,...,yt)=P(yt∣xt)P(xt∣y1,...,yt−1)



结论
- x t ∣ y 1 , . . . , y t − 1 = A E [ x t − 1 ] + A Δ X t − 1 + ω x_t|y_1,...,y_{t-1}=AE[x_{t-1}]+A\Delta X_{t-1}+\omega xt∣y1,...,yt−1=AE[xt−1]+AΔXt−1+ω = E [ x t ] + Δ x t =E[x_t]+\Delta x_t =E[xt]+Δxt
- y t ∣ y 1 , . . . y t − 1 = H A E [ X t − 1 ] + H A Δ x t − 1 + H ω + v = E [ y t ] + Δ y t y_t|y_1,...y_{t-1} = HAE[X_{t-1}]+HA \Delta x_{t-1}+H\omega + v = E[y_t] + \Delta y_t yt∣y1,...yt−1=HAE[Xt−1]+HAΔxt−1+Hω+v=E[yt]+Δyt
- P ( x t ∣ y 1 , . . . , y t ) = N ( A E [ x t − 1 ] , E [ ( Δ x ) ( Δ x ) T ] ) P(x_t|y_1,...,y_t) = N(AE[x_{t-1}],E[(\Delta x)(\Delta x)^T]) P(xt∣y1,...,yt)=N(AE[xt−1],E[(Δx)(Δx)T])
- P ( y t ∣ y 1 , . . . , y t − 1 ) = N ( H A E [ X t − 1 ] , E [ ( Δ y ) ( Δ y ) T ] ) P(y_t|y1,...,y_{t-1}) = N(HAE[X_{t-1}],E[(\Delta y)(\Delta y)^T]) P(yt∣y1,...,yt−1)=N(HAE[Xt−1],E[(Δy)(Δy)T])
以上为边缘分布
P ( x t , y t ∣ y 1 , . . . , y t − 1 ) P(x_t,y_t|y_1,...,y_{t-1}) P(xt,yt∣y1,...,yt−1)

非线性非高斯噪声的动态模型
相关文章:

徐亦达机器学习:Kalman Filter 卡尔曼滤波笔记 (一)
P ( x t P(x_t P(xt| x t − 1 ) x_{t-1}) xt−1) P ( y t P(y_t P(yt| x t ) x_t) xt) P ( x 1 ) P(x_1) P(x1)Discrete State DM A X t − 1 , X t A_{X_{t-1},X_t} AXt−1,XtAny π \pi πLinear Gassian Kalman DM N ( A X t − 1 B , Q ) N(AX_{t-1}B,Q)…...

Java和vue的包含数组组件contains、includes
List<String> tempList Arrays.asList("10018","1007","10017","1012"); if(tempList.contains(initMap.get("asset_type_id").toString())){// todo 计算运营终点桩号-起点桩号BigDecimal diffSum collectNum(col…...
OpenCV_CUDA_VS编译安装
一、OpenCV 我这里是下载的OpenCV4.5.4,但是不知道到在vs里面build时一直报错,后面换了4.7.0的版本测试,安装成功。 Release OpenCV 4.5.4 opencv/opencv GitHub 这个里面有官方预编译好的OpenCV库,可以直接食用。 扩展包&am…...
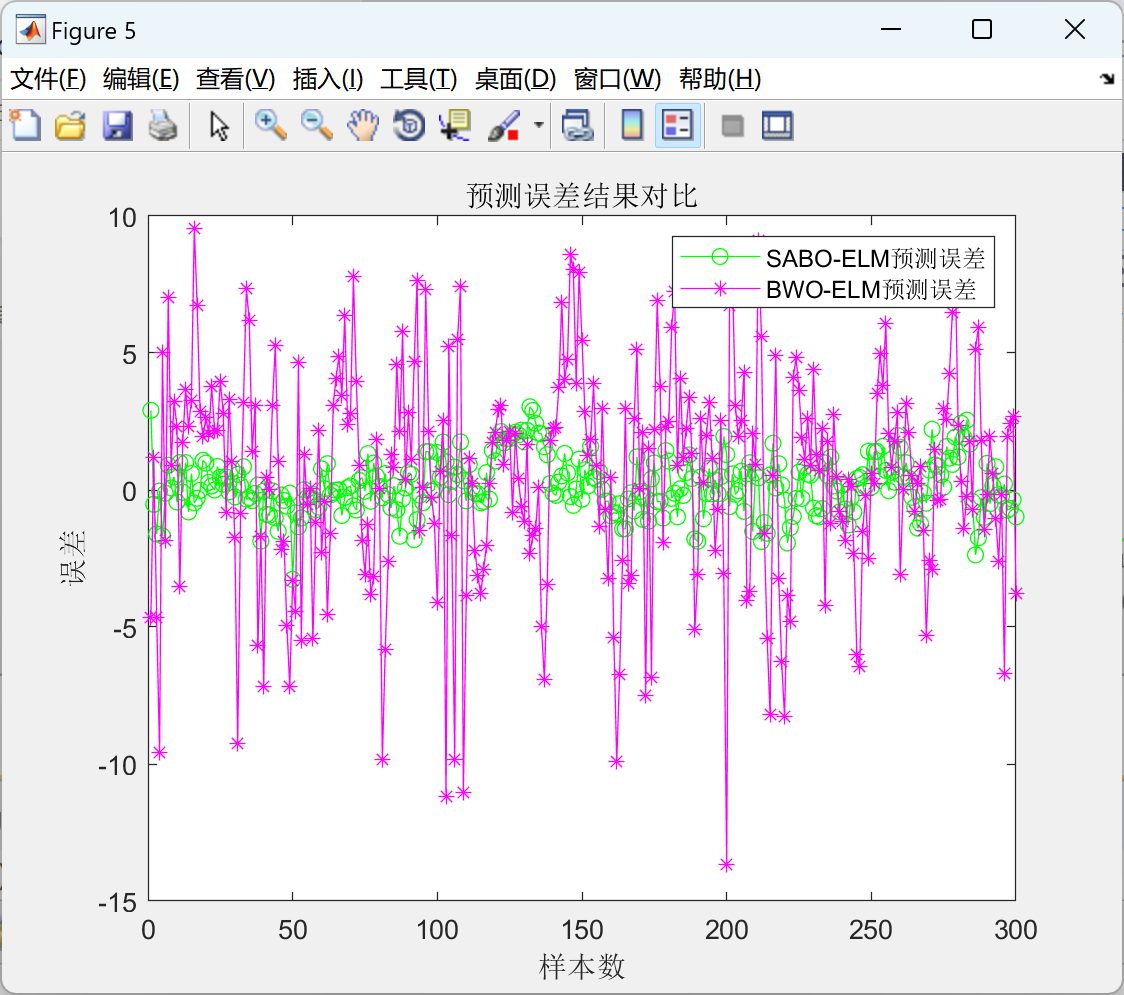
基于减法优化SABO优化ELM(SABO-ELM)负荷预测(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

记录第一个启动代码的诞生
核使用R52,参考汇编模板,一步一步来实现。 首先是ld文件,这个没啥好说的,主要是关注给vector_table划一块地址、stack地址,如下: .text.intvec :{_vectors_start .;KEEP(*(.text.intvec))_vectors_end .;…...
基于STM32的简化版智能手表
一、前言 本文的OLED多级菜单UI为一个综合性的STM32小项目,使用多传感器与OLED显示屏实现智能终端的效果。项目中的多级菜单UI使用了较为常见的结构体索引法去实现功能与功能之间的来回切换,搭配DHT11,RTC,LED,KEY等器…...

揭秘弹幕游戏制作
最近好多人问弹幕游戏,甚至是招人的也要DOTS做弹幕游戏... 实际上目前的弹幕游戏绝大多数应该和DOTS没有半点关系,别忘了DOTS这项技术渲染问题还没能够被合理解决呢 所以目前用的全都是GPU Instance这项技术,于是乎我决定下场写这篇帖子&am…...
2327. 知道秘密的人数;1722. 执行交换操作后的最小汉明距离;2537. 统计好子数组的数目
2327. 知道秘密的人数 核心思想:动态规划,每天的人可以分为三种,可分享秘密的人,不可分享秘密的人,忘记秘密的人。定义f[i]为第i天可分享秘密的人,那么第(idelay ,iforget)天,会增加f[i]个可分…...
【TCPDF】使用TCPDF导出PDF文件
目录 一、安装TCPDF类库 二、安装字体 三、使用TCPDF导出PDF文件 目的:PHP通过TCPDF类库导出文件为PDF。 开发语言及类库:ThinkPHP、TCPDF 效果图如下 一、安装TCPDF类库 在项目根目录使用composer安装TCPDF,安装完成后会在vendor目录下…...

MacBook苹果电脑重装、降级系统
1、下载balenaEtcher镜像启动盘制作工具 https://tails.net/etcher/balenaEtcher-portable.exe 2、选择从文件烧录选择下载好的Mac 镜像文件 百度网盘 请输入提取码(Mac OS 10.10-12版本镜像文件) 第二步选择目标磁盘,这里需要准备一块1…...

Java 解决long类型数据在前后端传递失真问题
问题:雪花算法的id长度为19位,前端能够接收的数字最多只能是16位的,因此就会造成精度丢失,得到的ID不是真正的ID。 解决: 在拦截器中加入Long类型转换,返回给前端string package io.global.iot.common.c…...
IDEA的快捷键大全
快捷键 说明 IntelliJ IDEA 的便捷操作性,快捷键的功劳占了一大半,对于各个快捷键组合请认真对待。IntelliJ IDEA 本身的设计思维是提倡键盘优先于鼠标的,所以各种快捷键组合层出不穷,对于快捷键设置也有各种支持,对…...

简单记一下Vue router 路由中使用 vue-i18n 进行标题国际化
引入状态管理和国际化文件 import store from ../store import i18n from /configs/i18n使用状态管理设置路由当前国际化选项 // 使用状态管理 i18n.locale store.state.setStore.i18n??zh路由中使用i18n { path: /login, name: login, component: LoginPage, meta: { ti…...

【Gitea】 Post “http://localhost:3000/api/internal/hook/pre-receive/aa/bbb“ 异常
引 使用 JGit 做了一个发布代码到 Gitea 的接口,使用该接口发布代码到 http://xxx-local/{name}/{project} ,报了 Post "http://localhost:3000/api/internal/hook/pre-receive/{name}/{project} 相关的异常。具体内容如下: Gitea: In…...
如何使用element-ui相关组件如:el-select,el-table,el-switch,el-pagination,el-dialog
element-ui 官方链接: 组件 | Elementhttps://element.eleme.cn/#/zh-CN/component/installation el-select <!-- 用户类型选择框<template> 看情况使用value选择框绑定的值 命名必须是value不能改v-for"item in Options" options数据源来自于…...

微信小程序+echart实现点亮旅游地图
背景 最近看抖音有个很火的特效就是点亮地图,去过哪些地方,于是乎自己也想做一个,结合自己之前做的以家庭为单位的小程序,可以考虑做一个家庭一起点亮地图的功能。 效果图 过程 1,首先就是得去下微信小程序适配的ec…...
——Git命令总结)
Git(8)——Git命令总结
一、简介 本篇文章将基于Git(4)——Git命令小总结,补充后续的Git使用命令 二、总结 # 添加远程连接 git remote add origin 远端地址# 推送本地代码 git push origin 分支名称# 拉取远端代码(第一次) git clone 远端克隆地址# 更新远端代码…...

9.15 滴滴笔试
T1(二分) #include <bits/stdc.h>#define endl \nusing namespace std;typedef long long LL;const int N 1e5 10;int n, k; int a[N];bool check(int mid) {int rec 1e9, cnt 1;for(int i 0; i < n; i ) {int j i;while(j < n &…...
有趣的设计模式——适配器模式让两脚插头也能使用三孔插板
版权声明 本文原创作者:谷哥的小弟作者博客地址:http://blog.csdn.net/lfdfhl 场景与问题 众所周知,我们国家的生活用电的电压是220V而笔记本电脑、手机等电子设备的工作压没有这么高。为了使笔记本、手机等设备可以使用220V的生活用电就需…...
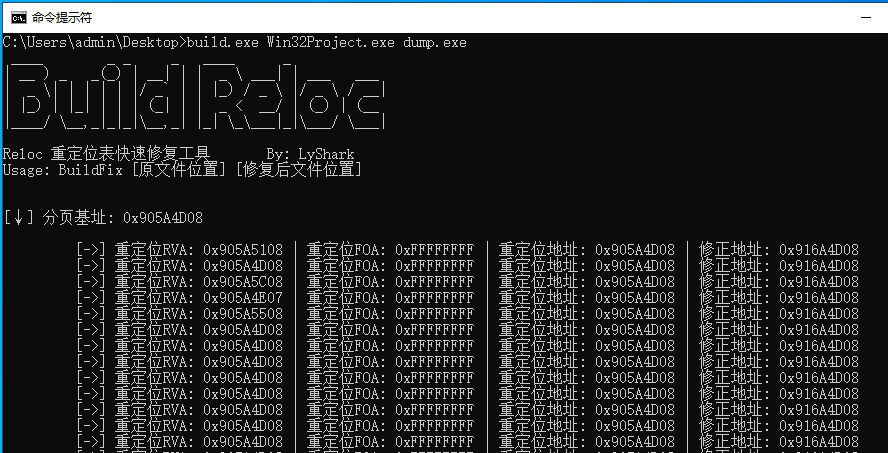
2.10 PE结构:重建重定位表结构
Relocation(重定位)是一种将程序中的一些地址修正为运行时可用的实际地址的机制。在程序编译过程中,由于程序中使用了各种全局变量和函数,这些变量和函数的地址还没有确定,因此它们的地址只能暂时使用一个相对地址。当…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
