栈与队列经典题目——用队列实现栈
本篇文章讲解栈和队列这一部分知识点的经典题目:用栈实现队列、用队列实现栈。对应的题号分别为:Leetcode.225——用队列实现栈,。
在对两个题目进行解释之前,先回顾以下栈和队列的特点与不同:
栈是一种特殊的线性表,并且只能在尾部进行插入、删除的操作。对于栈的实现,可以通过顺序表或者链表的思路来达成。但是,参考栈只能在尾部进行插入、删除操作的特点。一般采用顺序表进行实现。
队列也是一种特殊的线性表,只能在队尾进行插入操作,在队头进行删除操作。鉴于队列的这一性质,一般采用链表来实现队列。
1.Leetcode.225——用队列实现栈:
题目如下:
1.1 思路分析:
给出下列一个栈:
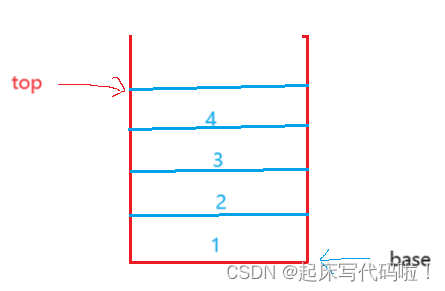
在栈中,遵从后进先出的原则。但是,本题要求是利用队列来实现栈。对于队列来说,出数据只能从队头进行。题目中要求利用两个队列来实现栈的功能,对于本功能,思路如下:
给定下面两个队列,分别命名为,
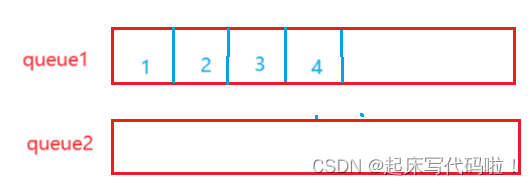
按照题目中的要求,需要移除元素。对于队列来说,移除元素只能从队头进行。所以,先把
中的元素
都移动到
中。此时效果如下:
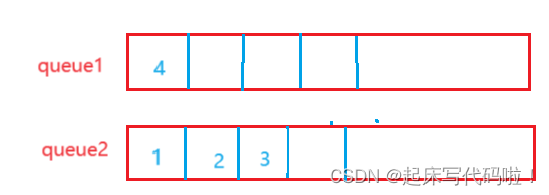
此时,再对进行一次取队头元素的操作即可。 下面为了方便表达,将
简称为
,
简称为
由上述分析可知。解决本题的关键就是在使用两个队列时,需要让一个队列中存储元素,另一个队列保持为空。当需要进行返回栈顶元素的操作时,再让为空的队列保存另一个队列中的前项元素。所以,
一个队列用于存储元素,一个用于保持空状态为了方便表达。下面,会默认创建两个结构体指针:
,来存储
的地址,
来存储
的地址。并在后续会针对二者谁为空进行判断。
(注:下面只给出各种给定功能的实现方法,在进行解题时,需要预先将编写好的xiami码复制到题目上方,本文采用一起学数据结构(6)——栈和队列_起床写代码啦!的博客-CSDN博客
中的队列)
1.2 各功能的实现:
1.2.1 栈的创建及初始化 :
:
前面说到,需要一个用于存储元素的队列,一个保持空状态的队列。但是对于二者谁为空,在后续的操作中进行判断即可。在本功能中不需要进行判断。代码如下:
//创建队列
typedef struct {Que q1;Que q2;
} MyStack;//初始化队列,注意,返回值返回地址,需要采用malloc返回以保证返回时不会因为变量的局部性成为野指针
MyStack* myStackCreate() {MyStack* obj = (MyStack*)malloc(sizeof(MyStack));QueueInit(&obj->q1);QueueInit(&obj->q2);return obj;
}1.2.2 向栈中插入元素myStackPush:
为了保证为空,
不为空,所以,在向栈中插入元素时,需要向
中插入。在初始化这一步骤中,并没有分辨哪个队列为空,在本步骤并不需要明确知道哪个队列为空,只需要利用
函数判断队列
是否为空,如果
为空,此时
为
,直接向
中进行插入,反之则向
中插入,代码如下:
void myStackPush(MyStack* obj, int x) {if(!QueueEmpty(&obj->q1)){QueuePush(&obj->q1,x);}else{QueuePush(&obj->q2,x);}
}1.2.3 移除并返回栈顶元素 myStackPop:
在思路分析中,已经给出了该功能的实现方法。即,让指向的队列中的前
项元素移动到
所对应的元素。在移动元素之前,需要先判断
哪个队列为空。方法如下:
首先创建结构体指针,
。让二者分别指向队列
。利用
函数判断此时的
是否为空,若为空,则不做改变。若不为空,则令
,
中存储的地址交换。
代码如下:
int myStackPop(MyStack* obj) {Que* noempty = &obj->q1;Que* empty = &obj->q2;if(!QueueEmpty(empty)){noempty = &obj->q2;empty = &obj->q1;} }
再判断出哪个队列为
,哪个队列为
后,进行下一步。首先,利用
函数取出
中的队头元素,再利用
函数将
取出的元素插入到
中。
题目要求,移除并且返回。所以需要额外创建一个变量用于存储栈顶元素。之后再利用
函数移除栈顶元素,最后返回
即可。代码如下:
int myStackPop(MyStack* obj) {Que* noempty = &obj->q1;Que* empty = &obj->q2;if(!QueueEmpty(empty)){noempty = &obj->q2;empty = &obj->q1;}while( QueueSize(noempty) > 1){QueuePush(empty,QueueFront(noempty));QueuePop(noempty);}int Top = QueueFront(noempty);QueuePop(noempty);return Top;}1.2.4 返回栈顶元素myStackTop:
栈顶元素所对应的位置就是队列的队尾。所以,只需要采用向栈中插入元素的方法,通过函数,对不满足
的队列(即非空队列)调用
函数,返回函数的返回值即可。代码如下:
int myStackTop(MyStack* obj) {if(!QueueEmpty(&obj->q1)){return QueueBack(&obj->q1);}else{return QueueBack(&obj->q2);}
}1.2.5 探空myStackEmpty:
原理较为简单,只给出代码:
bool myStackEmpty(MyStack* obj) {return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);}1.2.6 释放动态开辟的空间myStackFree:
代码如下:
void myStackFree(MyStack* obj) {QueueDestory(&obj->q1);QueueDestory(&obj->q2);free(obj);
}2.结果展示及题解代码总览:
2.1 结果展示:
2.2 题解代码总览:
typedef int QDataType;
typedef struct QueueNode
{struct QueueNode* next;QDataType data;
}QNode;typedef struct Queue
{QNode* phead;QNode* tail;int size;
}Que;//初始化
void QueueInit(Que* ps);
//销毁
void QueueDestory(Que* ps);
//插入元素
void QueuePush(Que* ps, QDataType x);
//删除元素
void QueuePop(Que* ps);
//取头部元素
QDataType QueueFront(Que* ps);
//取尾部元素
QDataType QueueBack(Que* ps);
//探空
bool QueueEmpty(Que* ps);
//求长度
int QueueSize(Que* ps);void QueueInit(Que* ps)
{assert(ps);ps->phead = ps->tail = 0;ps->size = 0;
}void QueuePush(Que* ps, QDataType x)
{assert(ps);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc");exit(-1);}newnode->next = NULL;newnode->data = x;if (ps->tail == NULL){ps->phead = ps->tail = newnode;}else{ps->tail->next = newnode;ps->tail = newnode;}ps->size++;
}void QueuePop(Que* ps)
{assert(ps);assert(!QueueEmpty(ps));if (ps->phead->next == NULL){free(ps->phead);ps->phead = ps->tail = NULL;}else{QNode* next = ps->phead->next;free(ps->phead);ps->phead = next;}ps->size--;
}QDataType QueueFront(Que* ps)
{assert(ps);assert(!QueueEmpty(ps));return ps->phead->data;
}QDataType QueueBack(Que* ps)
{assert(ps);assert(!QueueEmpty(ps));return ps->tail->data;
}bool QueueEmpty(Que* ps)
{assert(ps);return ps->phead == NULL;
}int QueueSize(Que* ps)
{assert(ps);return ps->size;
}void QueueDestory(Que* ps)
{assert(ps);QNode* cur = ps->phead;while (cur){QNode* next = cur->next;free(cur);cur = next;}ps->phead = ps->tail = NULL;ps->size = 0;
}//创建队列
typedef struct {Que q1;Que q2;
} MyStack;//初始化队列,注意,返回值返回地址,需要采用malloc返回以保证返回时不会因为变量的局部性成为野指针
MyStack* myStackCreate() {MyStack* obj = (MyStack*)malloc(sizeof(MyStack));QueueInit(&obj->q1);QueueInit(&obj->q2);return obj;
}void myStackPush(MyStack* obj, int x) {if(!QueueEmpty(&obj->q1)){QueuePush(&obj->q1,x);}else{QueuePush(&obj->q2,x);}
}//思路:将非空队列中前N-1项元素移到空队列中
int myStackPop(MyStack* obj) {Que* noempty = &obj->q1;Que* empty = &obj->q2;if(!QueueEmpty(empty)){noempty = &obj->q2;empty = &obj->q1;}while( QueueSize(noempty) > 1){QueuePush(empty,QueueFront(noempty));QueuePop(noempty);}int Top = QueueFront(noempty);QueuePop(noempty);return Top;}int myStackTop(MyStack* obj) {if(!QueueEmpty(&obj->q1)){return QueueBack(&obj->q1);}else{return QueueBack(&obj->q2);}
}bool myStackEmpty(MyStack* obj) {return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);}void myStackFree(MyStack* obj) {QueueDestory(&obj->q1);QueueDestory(&obj->q2);free(obj);
}
相关文章:
栈与队列经典题目——用队列实现栈
本篇文章讲解栈和队列这一部分知识点的经典题目:用栈实现队列、用队列实现栈。对应的题号分别为:Leetcode.225——用队列实现栈,。 在对两个题目进行解释之前,先回顾以下栈和队列的特点与不同: 栈是一种特殊的线性表…...
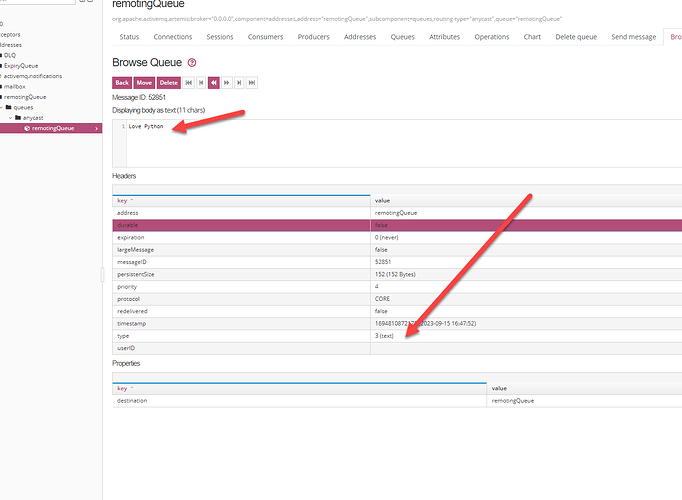
Python stomp 发送消息无法显示文本
我们向消息服务器通过 stomp 发送的是文本消息。 当消息服务器发送成功后,消息服务器上的文本没有显示,显示的是 2 进制的数据。 如上图,消息没有作为文本来显示。 问题和解决 消息服务器是如何判断发送的小时是文本还是二进制的。 根据官…...
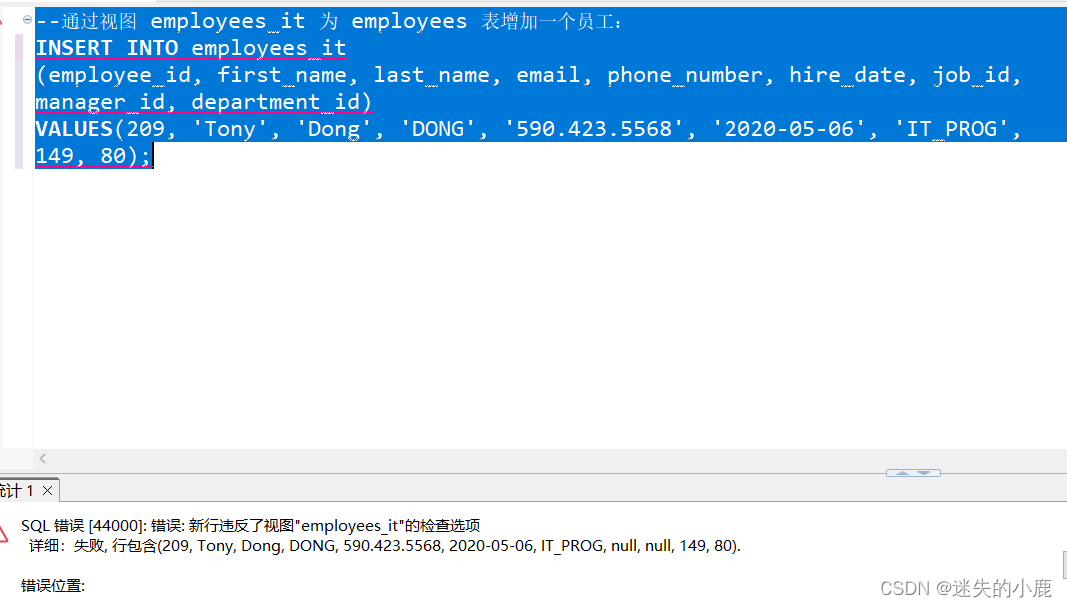
postgresql-视图
postgresql-视图 视图概述使用视图的好处 创建视图修改视图删除视图递归视图可更新视图WITH CHECK OPTION 视图概述 视图(View)本质上是一个存储在数据库中的查询语句。视图本身不包含数据,也被称为 虚拟表。我们在创建视图时给它指定了一个…...

科技资讯|Vision Pro头显无损音频仅限USB-C AirPods Pro 2耳机
彭博社的马克・古尔曼在最新发布的推文中表示,苹果 Vision Pro 头显的无损音频仅限于 USB-C AirPods Pro 2 耳机。 新款采用 USB-C 的 AirPods Pro 2 升级到了 IP54 级别(原版不防尘,仅 IPX4 级抗水),可陪伴用户在恶劣…...
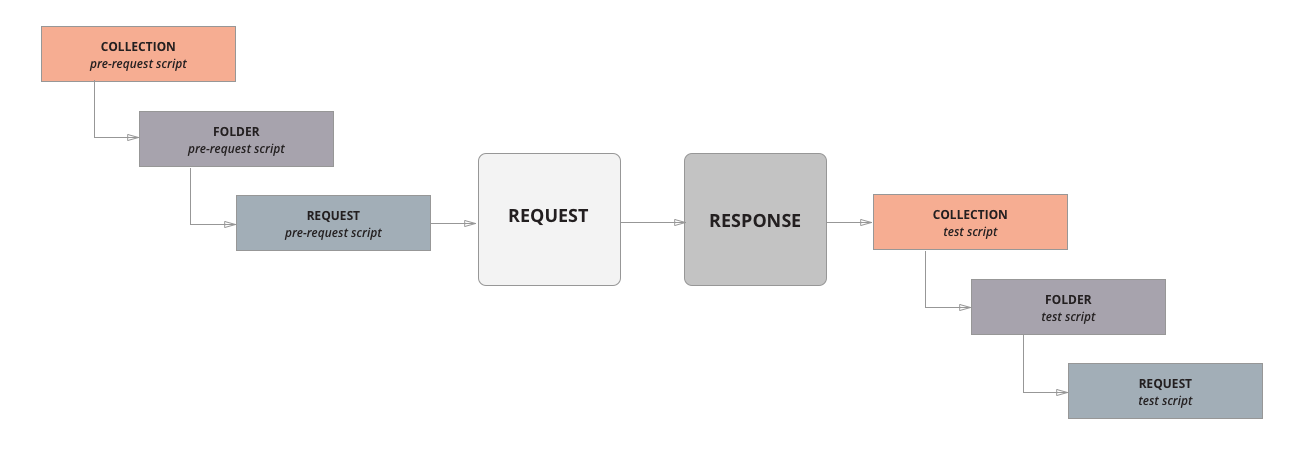
Postman应用——初步了解postman
Postman 是一个用于构建和使用 API 的 API 平台,Postman 简化了 API 生命周期的每个步骤并简化了协作,可以更快地创建更好的 API。 Postman 包含一个基于Node.js的强大的运行时,允许您向请求(request)和分组ÿ…...

分析报告显示,PHP是编程语言主力军,且在电商领域占据“统治地位”
日前有有业内专家透露了PHP语言的使用数据,并强调了PHP语言对于互联网的作用。 而根据W3 Techs发布的《全球前1000万个网站使用的编程语言分析(截至 2023.8)》中,有这样一组数据引起广泛的关注。PHP占比 77.2%、ASP占比 6.9%、Ruby 占比5.4%。 此外&am…...
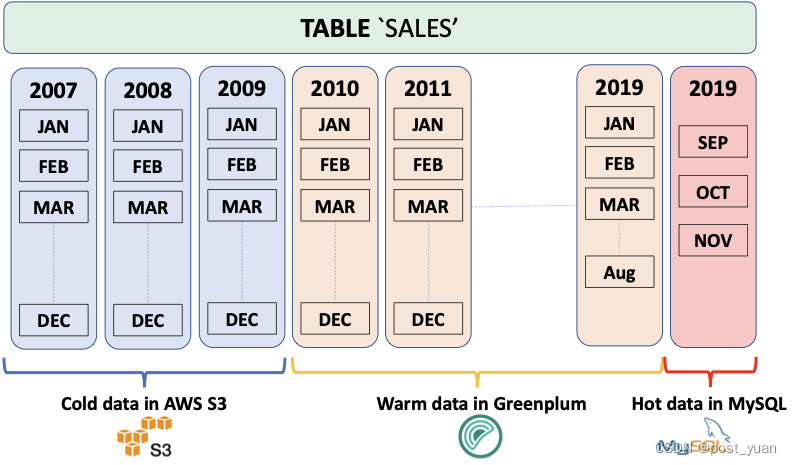
关于Greenplum Platform Extension Framework(PXF)
本文翻译自 https://docs.vmware.com/en/VMware-Greenplum-Platform-Extension-Framework/6.6/greenplum-platform-extension-framework/overview_pxf.html 随着数据存储和云服务的爆炸式增长,数据现在以各种格式驻留在许多不同的系统中。通常,数据根据…...

编程获取图像中的圆半径
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 即将推出EmguCV的教程,请大家还稍作等待。 之前网友咨询如何获得图像中圆形的半径,其中有两个十字作为标定…...

什么是Scrum?如何实施Scrum(敏捷开发)以及敏捷工具
什么是Scrum? Scrum是一个敏捷开发框架,它是一个增量的、迭代的开发过程。它被广泛应用于敏捷软件开发,在Scrum中,开发过程由若干个短的迭代周期组成,每个迭代周期称为一个Sprint。 那么Scrum如何实施呢…...
提升运营效率:仓储可视化的实时监控与优化
当今,仓储管理已经不再是简单的储存和分发商品的过程。随着供应链的复杂性增加,企业需要更高效的方式来管理和优化其仓储运营。在这个背景下,仓储可视化成为了一项关键的技术,它利用先进的数字化工具和数据分析来提升仓储管理的效…...
)
代理模式和单一职责原理一文读懂(设计模式与开发实践 P6)
文章目录 代理模式实现保护代理虚拟代理单一职责原理代理和本体 - 接口一致性虚拟代理 - 合并请求缓存代理其他代理 代理模式 定义:为一个对象提供一个代用品 & 占位符,以便 控制对他的访问 关键:不方便直接访问某个对象或不满足需要的时…...
Linux网络编程|TCP编程
一.网络基础 1.1网络发展史 Internet-“冷战”的产物 1957年10月和11月,前苏联先后有两颗“Sputnik”卫星上天 1958年美国总统艾森豪威尔向美国国会提出建立DARPA (Defense Advanced Research Project Agency),即国防部高级研究计划署&#…...
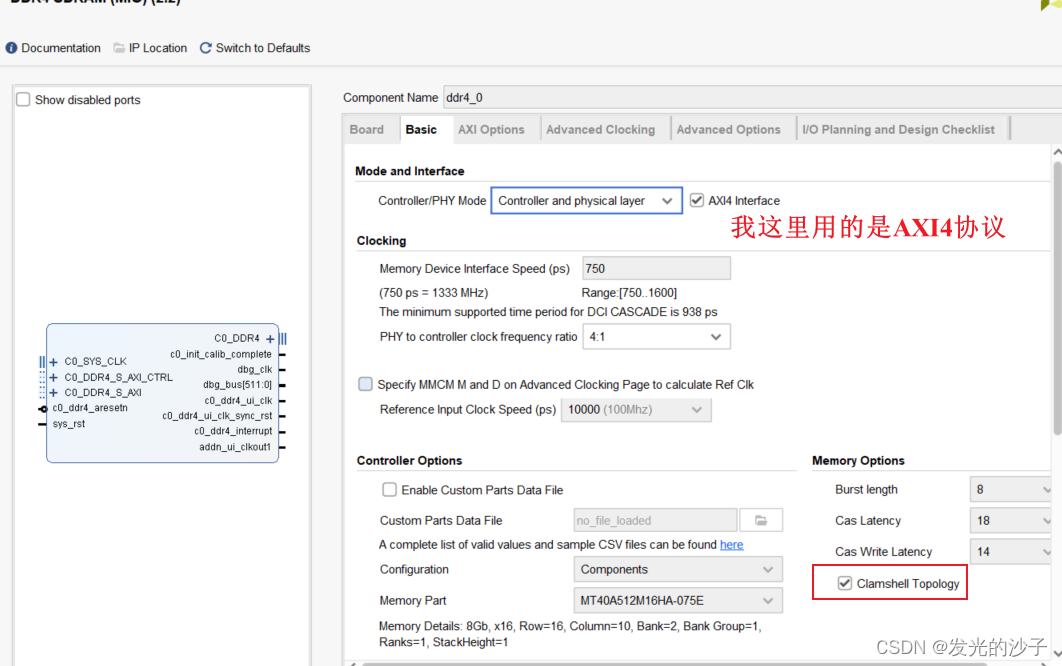
FPGA----VCU128的DDR4无法使用问题(全网唯一)
1、在Vivado 2019.1版本中使用DDR4的IP核会遇到如下图所示的错误,即便过了implementation生成了bit,DDR4也无法正常启动。 2、解决办法,上xilinx社区搜一下就知道了 AMD Customer Communityhttps://support.xilinx.com/s/article/69035?lan…...
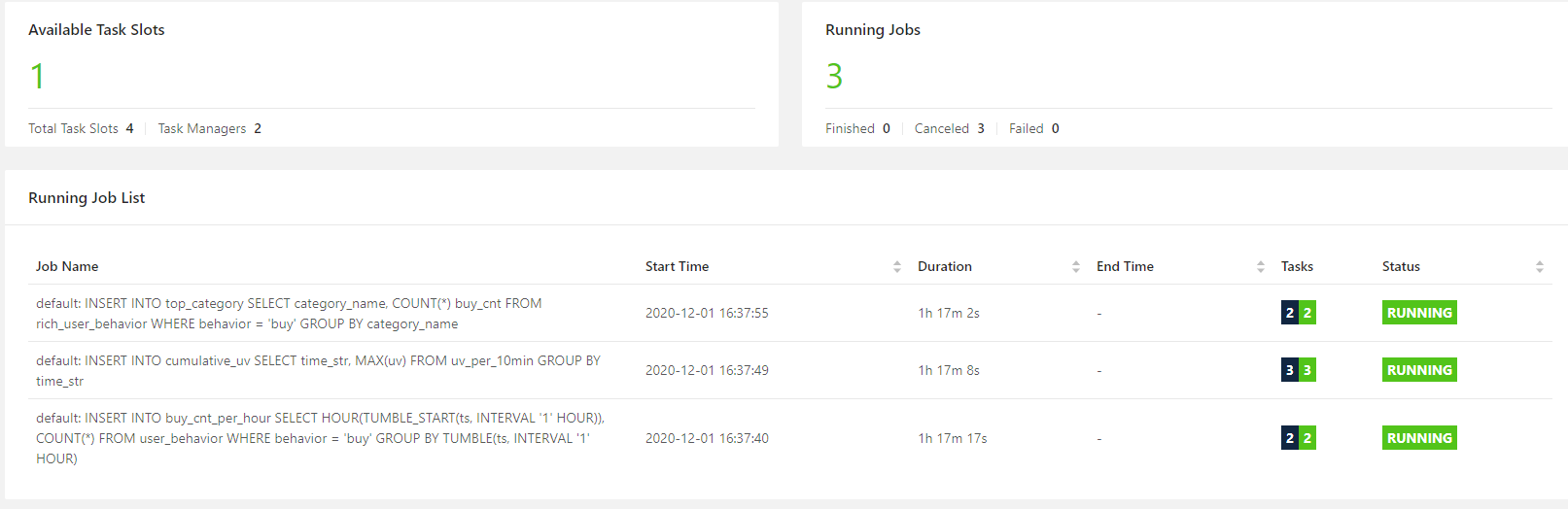
【毕设选题】flink大数据淘宝用户行为数据实时分析与可视化
文章目录 0 前言1、环境准备1.1 flink 下载相关 jar 包1.2 生成 kafka 数据1.3 开发前的三个小 tip 2、flink-sql 客户端编写运行 sql2.1 创建 kafka 数据源表2.2 指标统计:每小时成交量2.2.1 创建 es 结果表, 存放每小时的成交量2.2.2 执行 sql &#x…...
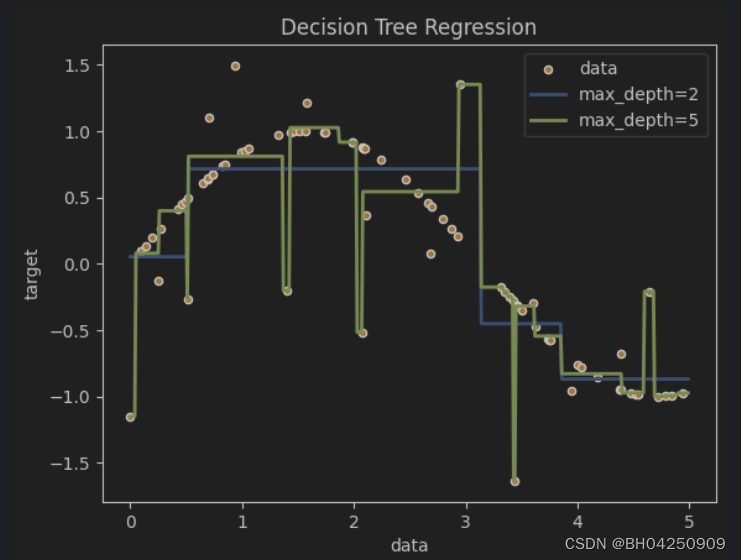
机器学习练习-决策树
机器学习练习-决策树 代码更新地址:https://github.com/fengdu78/WZU-machine-learning-course 代码修改并注释:黄海广,haiguang2000wzu.edu.cn 1.分类决策树模型是表示基于特征对实例进行分类的树形结构。决策树可以转换成一个if…...
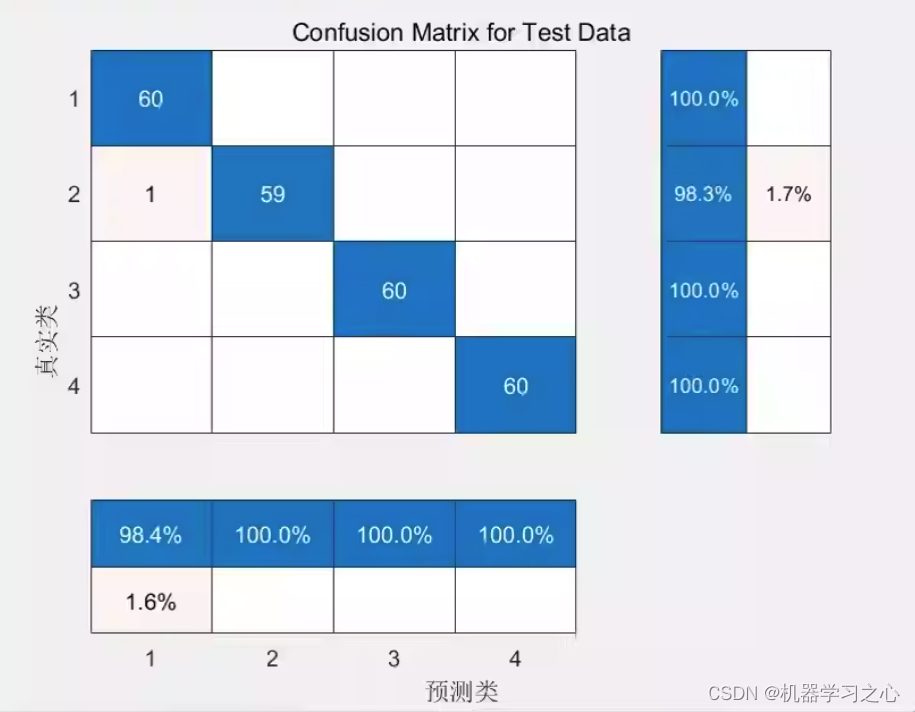
分类预测 | Matlab实现基于LFDA-SVM局部费歇尔判别数据降维结合支持向量机的多输入分类预测
分类预测 | Matlab实现基于LFDA-SVM局部费歇尔判别数据降维结合支持向量机的多输入分类预测 目录 分类预测 | Matlab实现基于LFDA-SVM局部费歇尔判别数据降维结合支持向量机的多输入分类预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 基于局部费歇尔判别数据降维的L…...
Say0l的安全开发-代理扫描工具-Sayo-proxyscan【红队工具】
写在前面 终于终于,安全开发也练习一年半了,有时间完善一下项目,写写中间踩过的坑。 安全开发的系列全部都会上传至github,欢迎使用和star。 工具链接地址 https://github.com/SAY0l/Sayo-proxyscan 工具简介 SOCKS4/SOCKS4…...

使用FFmpeg+ubuntu系统转化flac无损音频为mp3
功能需求如上题,我们来具体的操作一下: 1.先在ubuntu上面安装FFmpeg:sudo apt install ffmpeg 2.进入有flac音频文件的目录使用下述命令: ffmpeg -i test.FLAC -c:a libmp3lame -q:a 2 output.mp3 3.如果没有什么意外的话,你就能看到你的文件夹里面已经有转化好的mp3文件了 批…...

I/O多路复用三种实现
一.select 实现 (1)select流程 基本流程是: 1. 先构造一张有关文件描述符的表; fd_set readfds 2. 清空表 FD_ZERO() 3. 将你关心的文件描述符加入到这…...

DataInputStream数据读取 Vs ByteBuffer数据读取的巨大性能差距
背景: 今天在查找一个序列化和反序列化相关的问题时,意外发现使用DataInputStream读取和ByteBuffer读取之间性能相差巨大,本文就来记录下这两者在读取整数类型时的性能差异,以便在平时使用的过程中引起注意 DataInputStream数据…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅!
【把数组变成一棵树】有序数组秒变平衡BST,原来可以这么优雅! 🌱 前言:一棵树的浪漫,从数组开始说起 程序员的世界里,数组是最常见的基本结构之一,几乎每种语言、每种算法都少不了它。可你有没有想过,一组看似“线性排列”的有序数组,竟然可以**“长”成一棵平衡的二…...
