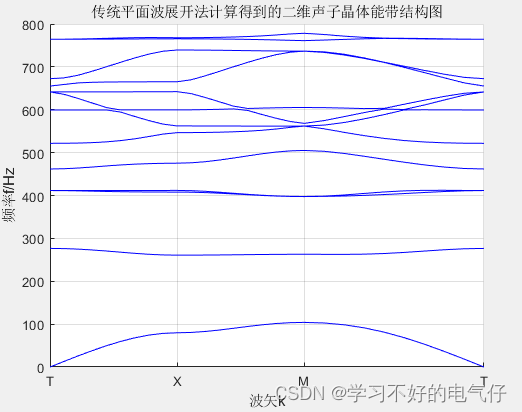
基于matlab实现的平面波展开法二维声子晶体能带计算程序
Matlab 平面波展开法计算二维声子晶体二维声子晶体带结构计算,材料是铅柱在橡胶基体中周期排列,格子为正方形。采用PWE方法计算
完整程序:
%%%%%%%%%%%%%%%%%%%%%%%%%
clear;clc;tic;epssys=1.0e-6; %设定一个最小量,避免系统截断误差或除零错误
%%%%%%%%%%%%%%%%%%%%%%%%%%
%定义实际的正空间格子基矢
%%%%%%%%%%%%%%%%%%%%%%%%%%
a=0.02;
a1=a*[1 0];
a2=a*[0 1];
%%%%%%%%%%%%%%%%%%%%%%%%%%
%定义晶格的参数
%%%%%%%%%%%%%%%%%%%%%%%%%%
rho1=11600;E1=4.08e10;mju1=1.49e10;lambda1=mju1*(E1-2*mju1)/(3*mju1-E1); %散射体的材料参数
rho2=1300;E2=1.175e5;mju2=4e4;lambda2=mju2*(E2-2*mju2)/(3*mju2-E2); %基体的材料参数
Rc=0.006; %散射体截面半径
Ac=pi*(Rc)^2; %散射体截面面积
Au=a^2; %二维格子原胞面积
Pf=Ac/Au; %填充率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%生成倒格基矢
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
b1=2*pi/a*[1 0];
b2=2*pi/a*[0 1];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%选定参与运算的倒空间格矢量,即参与运算的平面波数量
%设定一个l,m的取值范围,变化l,m即可得出参与运算的平面波集合
NrSquare=10; %选定倒空间的尺度,即l,m(倒格矢G=l*b1+m*b2)的取值范围。
%NrSquare确定后,使用Bloch波数目可能为(2*NrSquare+1)^2
G=zeros((2*NrSquare+1)^2,2); %初始化可能使用的倒格矢矩阵
i=1;
for l=-NrSquare:NrSquare
for m=-NrSquare:NrSquare
G(i,:)=l*b1+m*b2;
i=i+1;
end;
end;
NG=i-1; %实际使用的Bloch波数目
G=G(1:NG,:);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%生成k空间的rho(Gi-Gj),mju(Gi-Gj),lambda(Gi-Gj)值,i,j从1到NG。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
rho=zeros(NG,NG);mju=zeros(NG,NG);lambda=zeros(NG,NG);
for i=1:NG
for j=1:NG
Gij=norm(G(j,:)-G(i,:));
if (Gij<epssys)
rho(i,j)=rho1*Pf+rho2*(1-Pf);
mju(i,j)=mju1*Pf+mju2*(1-Pf);
lambda(i,j)=lambda1*Pf+lambda2*(1-Pf);
else
rho(i,j)=(rho1-rho2)*2*Pf*besselj(1,Gij*Rc)/(Gij*Rc);
mju(i,j)=(mju1-mju2)*2*Pf*besselj(1,Gij*Rc)/(Gij*Rc);
lambda(i,j)=(lambda1-lambda2)*2*Pf*besselj(1,Gij*Rc)/(Gij*Rc);
end;
end;
end;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%定义简约布里渊区的各高对称点
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
T=(2*pi/a)*[epssys 0];
M=(2*pi/a)*[1/2 1/2];
X=(2*pi/a)*[1/2 0];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%对于简约布里渊区边界上的每个k,求解其特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
THETA_A=zeros(NG,NG); %待解的本征方程A矩阵
THETA_B=zeros(NG,NG); %待解的本征方程B矩阵
Nkpoints=10; %每个方向上取的点数
stepsize=0:1/(Nkpoints-1):1; %每个方向上步长
TX_eig=zeros(Nkpoints,NG); %沿TX方向的波的待解的特征频率矩阵
XM_eig=zeros(Nkpoints,NG); %沿XM方向的波的待解的特征频率矩阵
MT_eig=zeros(Nkpoints,NG); %沿MT方向的波的待解的特征频率矩阵
for n=1:Nkpoints
fprintf(['\n k-point:',int2str(n),'of',int2str(Nkpoints),'.\n']);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%对于TX(正方格子)方向上的每个k值,求解其特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
TX_step=stepsize(n)*(X-T)+T;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%n 求本征矩阵的元素
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:NG
for j=1:NG
kGi=TX_step+G(i,:);
kGj=TX_step+G(j,:);
THETA_A(i,j)=mju(i,j)*dot(kGi,kGj);
THETA_B(i,j)=rho(i,j);
end;
end;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%求解TX(正方格子)方向上的k矩阵的特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
TX_eig(n,:)=sort(sqrt(eig(THETA_A,THETA_B))).';
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%对于XM(正方格子)方向上的每个k值,求解其特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
XM_step=stepsize(n)*(M-X)+X;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%n 求本征矩阵的元素
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:NG
for j=1:NG
kGi=XM_step+G(i,:);
kGj=XM_step+G(j,:);
THETA_A(i,j)=mju(i,j)*dot(kGi,kGj);
THETA_B(i,j)=rho(i,j);
end;
end;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%求解XM(正方格子)方向上的k矩阵的特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
XM_eig(n,:)=sort(sqrt(eig(THETA_A,THETA_B))).';
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%对于MT(正方格子)方向上的每个k值,求解其特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
MT_step=stepsize(n)*(T-M)+M;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%n 求本征矩阵的元素
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:NG
for j=1:NG
kGi=MT_step+G(i,:);
kGj=MT_step+G(j,:);
THETA_A(i,j)=mju(i,j)*dot(kGi,kGj);
THETA_B(i,j)=rho(i,j);
end;
end;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%求解MT(正方格子)方向上的k矩阵的特征频率
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
MT_eig(n,:)=sort(sqrt(eig(THETA_A,THETA_B))).';
end;
fprintf('\n Calculation Time:%d sec',toc);
save pbs2D
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%绘制声子晶体能带结构图
%首先将特定方向(正方格子:TX,XM,MT)离散化
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
kaxis=0;
TXaxis=kaxis:norm(T-X)/(Nkpoints-1):(kaxis+norm(T-X));
kaxis=kaxis+norm(T-X);
XMaxis=kaxis:norm(M-X)/(Nkpoints-1):(kaxis+norm(X-M));
kaxis=kaxis+norm(X-M);
MTaxis=kaxis:norm(T-M)/(Nkpoints-1):(kaxis+norm(T-M));
kaxis=kaxis+norm(T-M);
Ntraject=3; %所需绘制的特定方向的数目
EigFreq=zeros(Ntraject*Nkpoints,1);
figure(1)
hold on;
Nk=Nkpoints;
for k=1:NG
for i=1:Nkpoints
EigFreq(i+0*Nk)=TX_eig(i,k)/(2*pi);
EigFreq(i+1*Nk)=XM_eig(i,k)/(2*pi);
EigFreq(i+2*Nk)=MT_eig(i,k)/(2*pi);
end;
plot(TXaxis(1:Nk),EigFreq(1+0*Nk:1*Nk),'b',...
XMaxis(1:Nk),EigFreq(1+1*Nk:2*Nk),'b',...
MTaxis(1:Nk),EigFreq(1+2*Nk:3*Nk),'b');
end;
grid on;
hold off;
titlestr='传统平面波展开法计算得到的二维声子晶体能带结构图';
title(titlestr);
xlabel('波矢k');
ylabel('频率f/Hz');
axis([0 MTaxis(Nkpoints) 0 800]);
set(gca,'XTick',[TXaxis(1) TXaxis(Nkpoints) XMaxis(Nkpoints) MTaxis(Nkpoints)]);
xtixlabel=char('T','X','M','T');
set(gca,'XTickLabel',xtixlabel);
相关文章:

基于matlab实现的平面波展开法二维声子晶体能带计算程序
Matlab 平面波展开法计算二维声子晶体二维声子晶体带结构计算,材料是铅柱在橡胶基体中周期排列,格子为正方形。采用PWE方法计算 完整程序: %%%%%%%%%%%%%%%%%%%%%%%%% clear;clc;tic;epssys1.0e-6; %设定一个最小量,避免系统截断误差或除零错…...
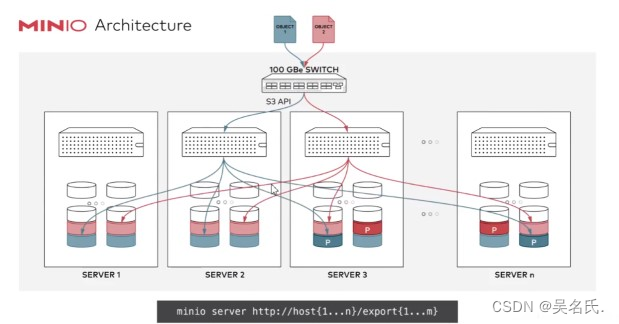
Minio入门系列【2】纠删码
1 纠删码 Minio使用纠删码erasure code和校验和checksum来保护数据免受硬件故障和无声数据损坏。 即便丢失一半数量(N/2)的硬盘,仍然可以恢复数据 1.1 什么叫纠删码 纠删码是一种用于重建丢失或损坏数据的数学算法。 纠删码(e…...
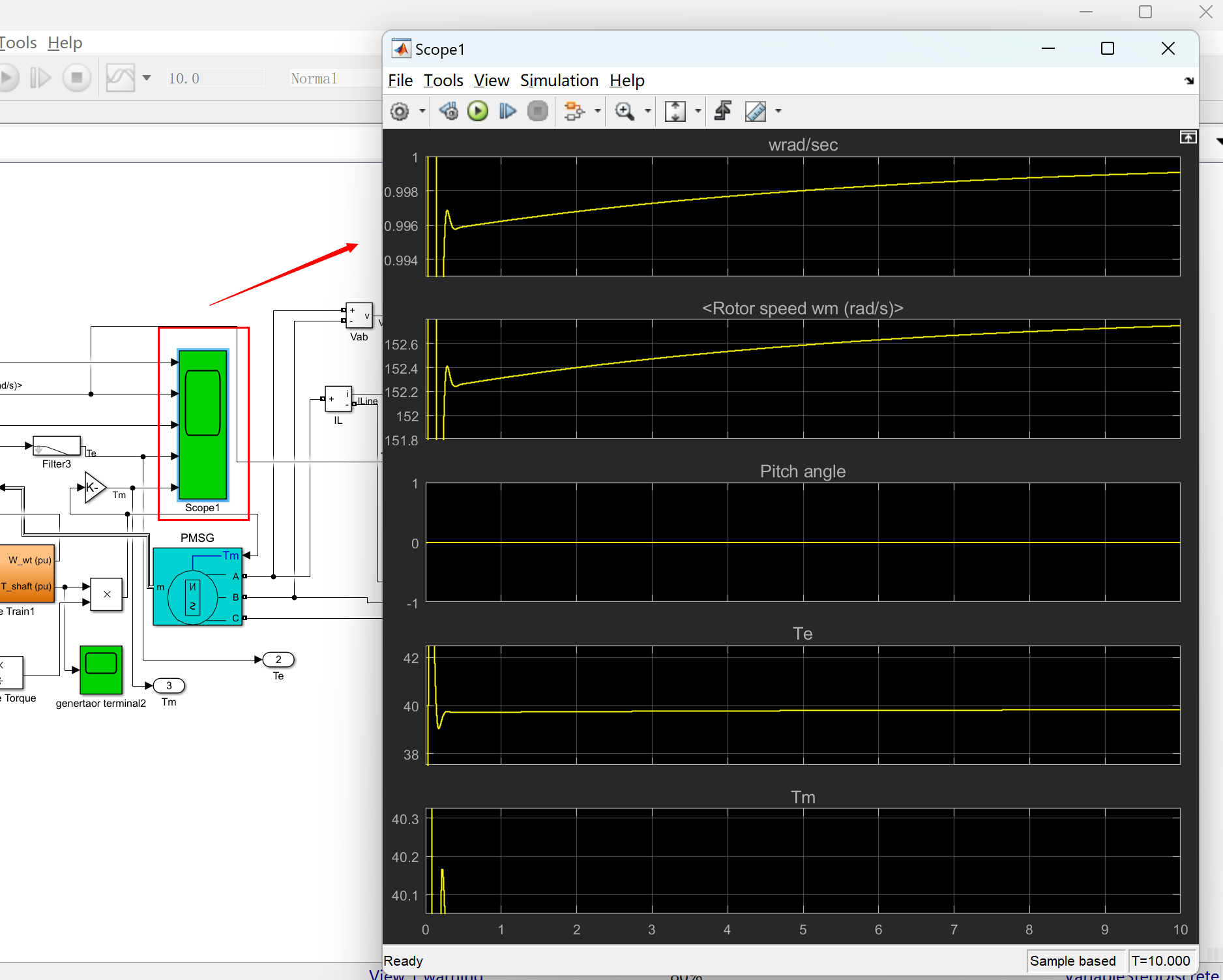
基于永磁同步发电机的风力发电系统研究(Simulink实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
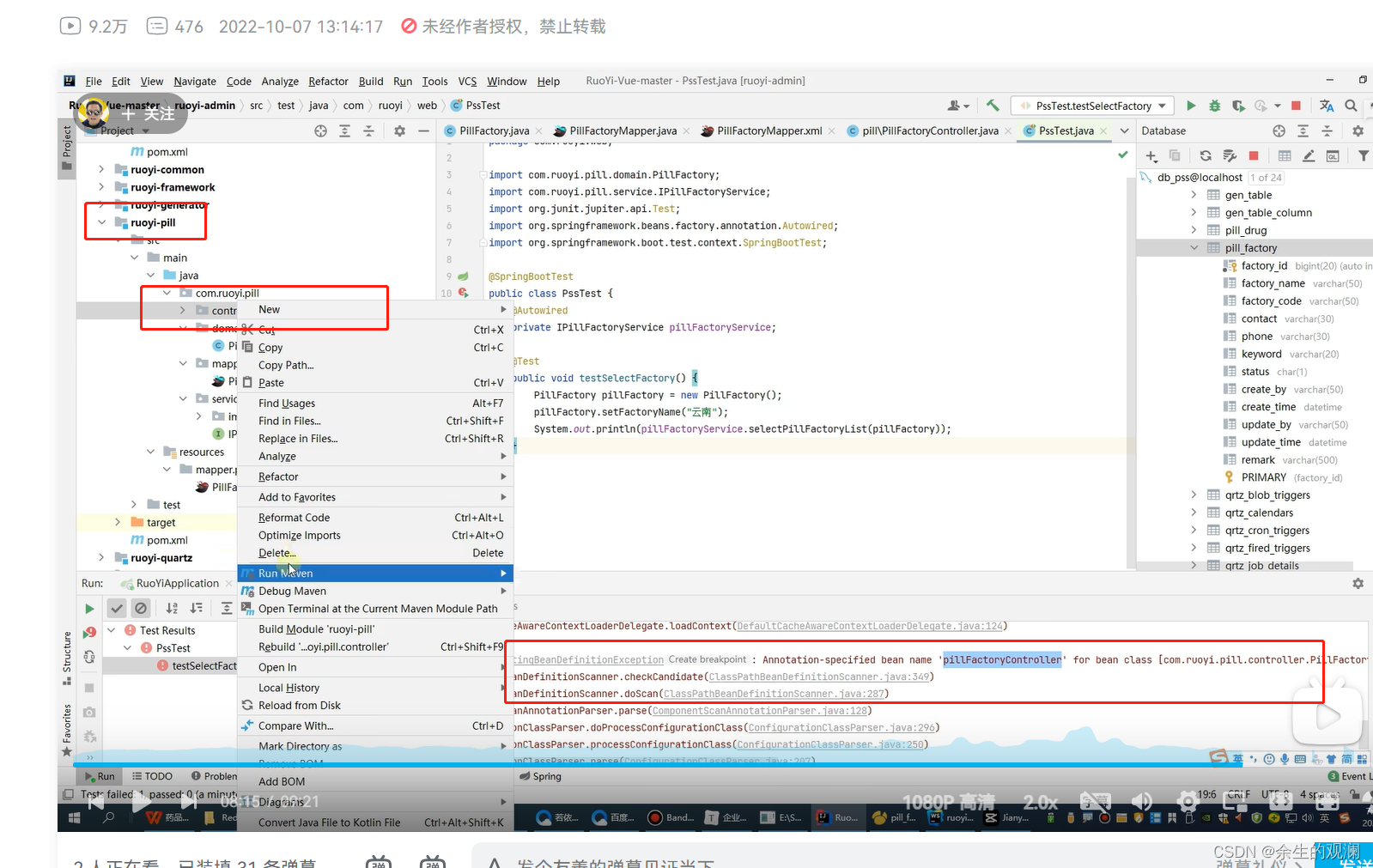
5.后端·新建子模块与开发(自动模式)
文章目录 学习资料自动生成模式创建后端三层 学习资料 https://www.bilibili.com/video/BV13g411Y7GS?p11&spm_id_frompageDriver&vd_sourceed09a620bf87401694f763818a31c91e 自动生成模式创建后端三层 首先,运行起来若依的前后端整个项目,…...
这样而不是data:{}这样?)
vue的data为什么要写成data(return{})这样而不是data:{}这样?
在Vue.js中,为什么要将data写成一个返回对象的函数data()而不是一个普通的对象data: {} 为什么? 因为Vue.js的组件实例是可复用的,而且它们可以在应用中多次实例化。通过将data定义为一个返回对象的函数,可以确保每个组件实例都…...

MySQL基础运维知识点大全
一. MySQL基本知识 1. 目录的功能 通用 Unix/Linux 二进制包的 MySQL 安装下目录的相关功能 目录目录目录binMySQLd服务器,客户端和实用程序docs信息格式的 MySQL 手册manUnix 手册页include包括(头)文件lib图书馆share用于数据库安装的错…...

javascript获取样式表的规则及读取与写入
CSSStyleSheet是继承了StyleSheet的接口属性,它是用于找当前文档中的<link rel“” href“”…>这样文件的,有以下属性:lenght,cssRules,title,href,type,deleteRule,insertRule等 CSSStyleRule是继承于CSSRule,它是用于找<link re…...

什么是promise?
是JavaScript中用于处理异步操作的一种机制。 异步操作,例如从服务器获取数据、读取文件、执行数据库查询等等。 经典使用:Axios 是一个基于Promise的HTTP客户端 Promise具有三个状态: Pending(待定):Pr…...

从零开始学习软件测试-第45天笔记
monkey事件 事件:对app进行的操作,比如触摸事件,滑动事件...动作:构成一个事件所需要的步骤。 调整事件的百分比 adb shell monkey -p 包名 -v -v --pct-xxx 百分比 次数>输出文件的路径 分析日志有没有报错 到日志中去找…...

visual studio常用快捷键
CtrlM、CtrlO 折叠到定义 CtrlM、CtrlM 折叠当前定义 CtrlM、CtrlA 折叠全部 CtrlK、CtrlD 自动编排代码格式 F12 转到定义 ShiftF12 查看所有定义 ctrl] 转到定义首部或尾部 ctrlX 未选中文本时,剪切/删除光标所在行。ctrlV 未选中文本时,粘贴到…...

数据变换:数据挖掘的准备工作之一
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...

Go语言实践案例之简单字典
一、程序要实现效果: 在命令行调用程序的时候,可以在命令行的后面查询一个单词,然后会输出单词的音标和注释。 二、思路分析: 定义一个结构体 DictRequest,用于表示翻译请求的数据结构。其中包含了 TransType&#…...
)
笔试面试相关记录(3)
(1)String String和String.append()的底层实现 C中string append函数的使用与字符串拼接「建议收藏」-腾讯云开发者社区-腾讯云 (tencent.com) String String 在 第二个String中遇到\0就截止,append()的方法则是所有字符都会加在后面。 &…...
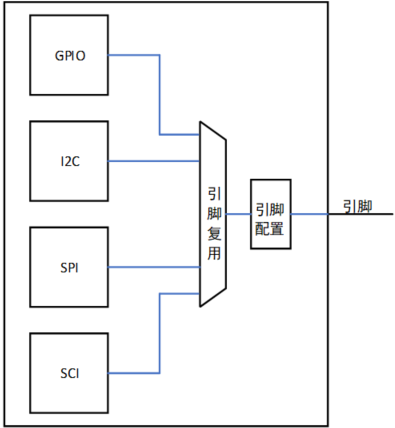
第6章_瑞萨MCU零基础入门系列教程之串行通信接口(SCI)
本教程基于韦东山百问网出的 DShanMCU-RA6M5开发板 进行编写,需要的同学可以在这里获取: https://item.taobao.com/item.htm?id728461040949 配套资料获取:https://renesas-docs.100ask.net 瑞萨MCU零基础入门系列教程汇总: ht…...

开源免费的流程图软件draw.io
2023年9月16日,周六上午 想买微软的visio,但发现不是很值得,因为我平时也不是经常需要画图。 所以我最后还是决定使用开源免费的draw.io来画图 draw.io网页版的网址: Flowchart Maker & Online Diagram Software draw.io的…...
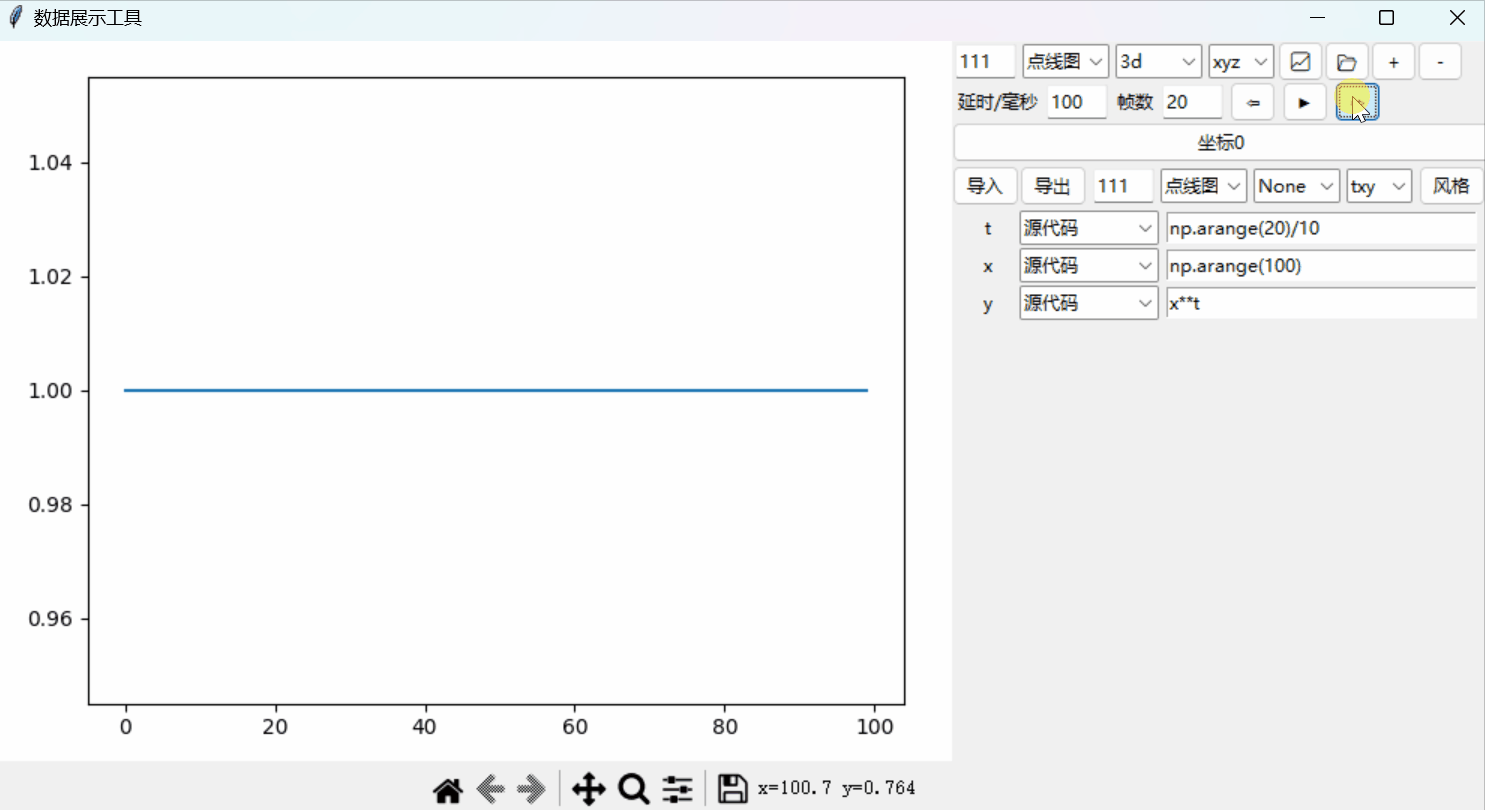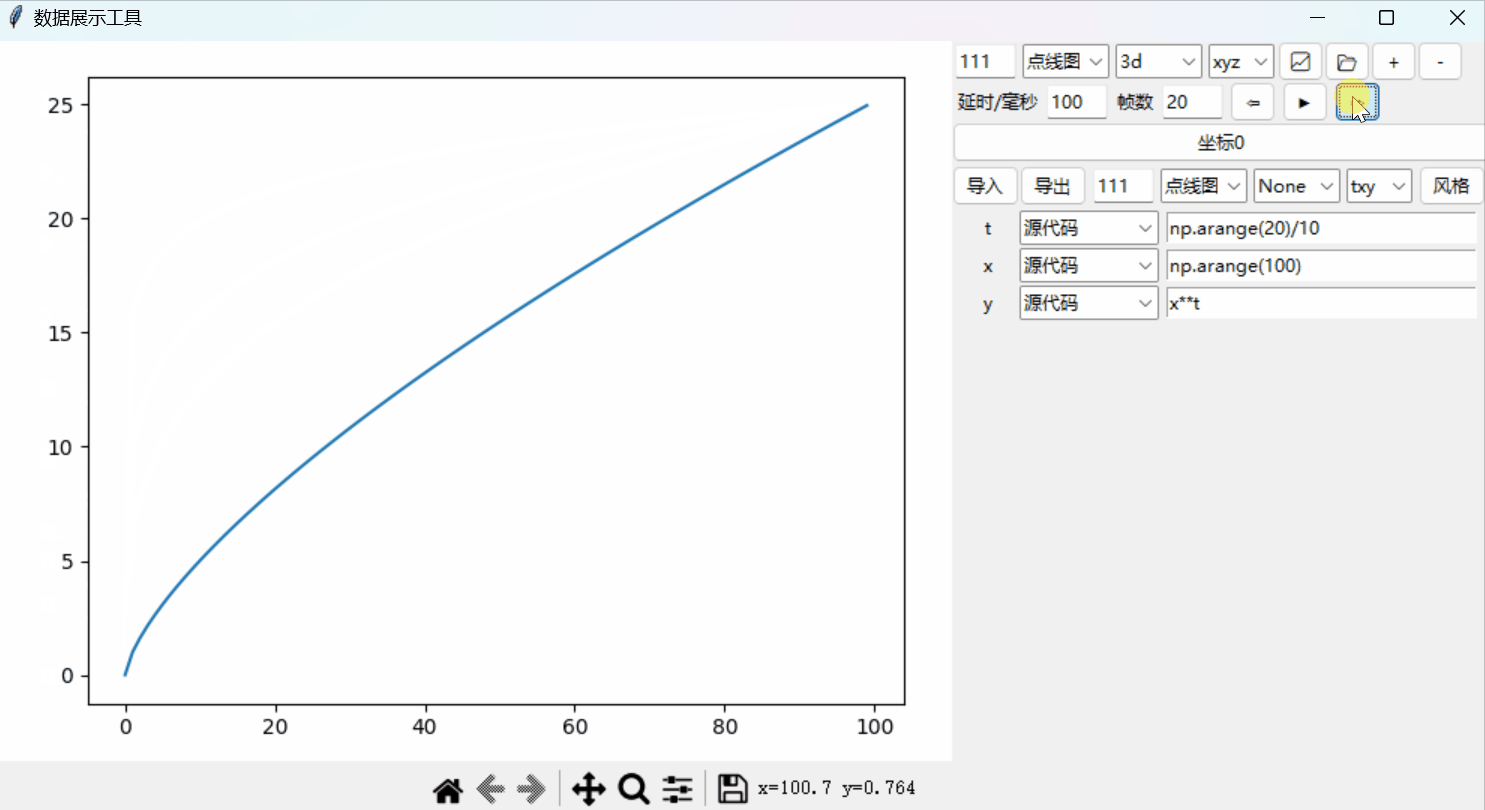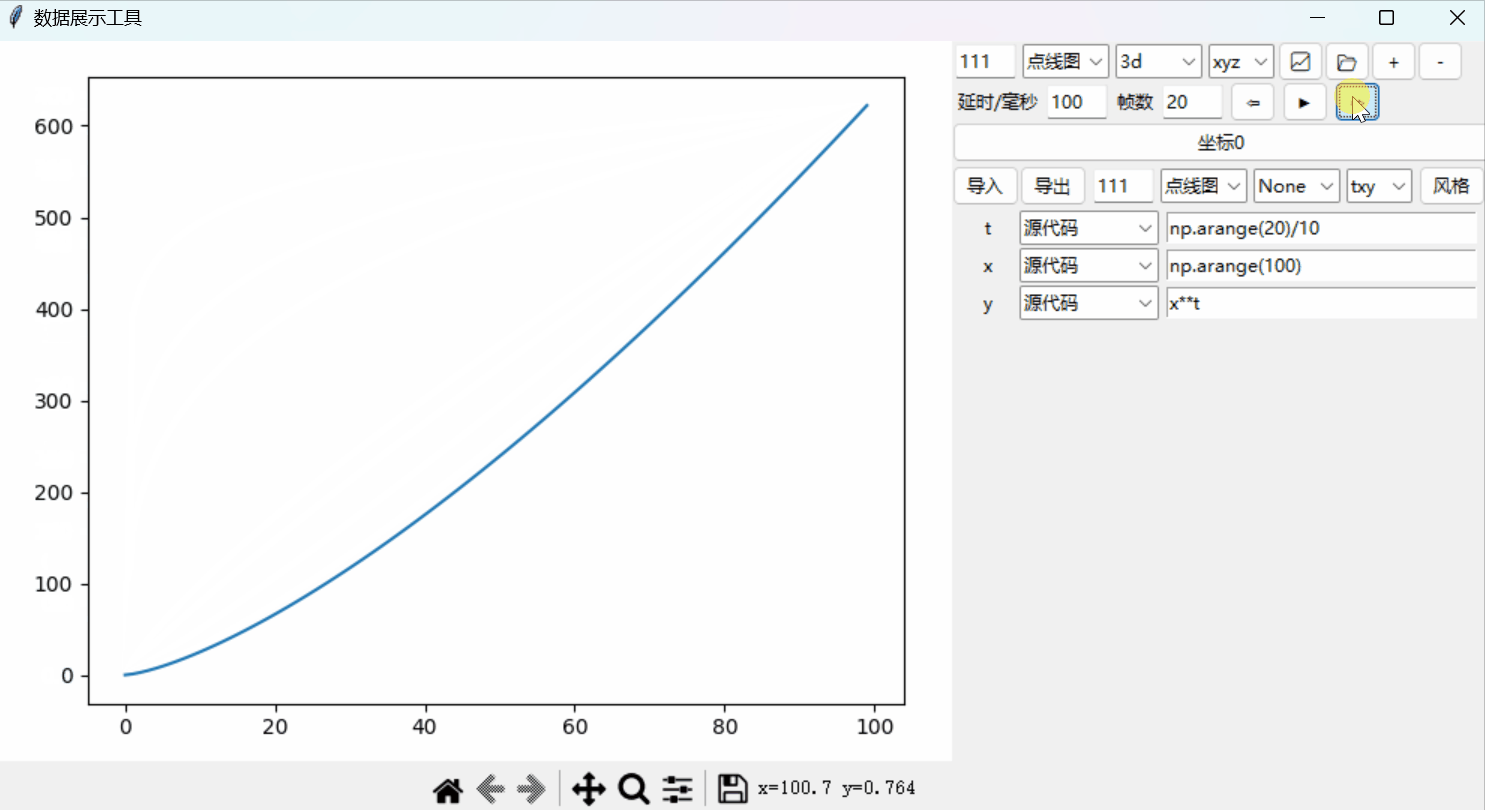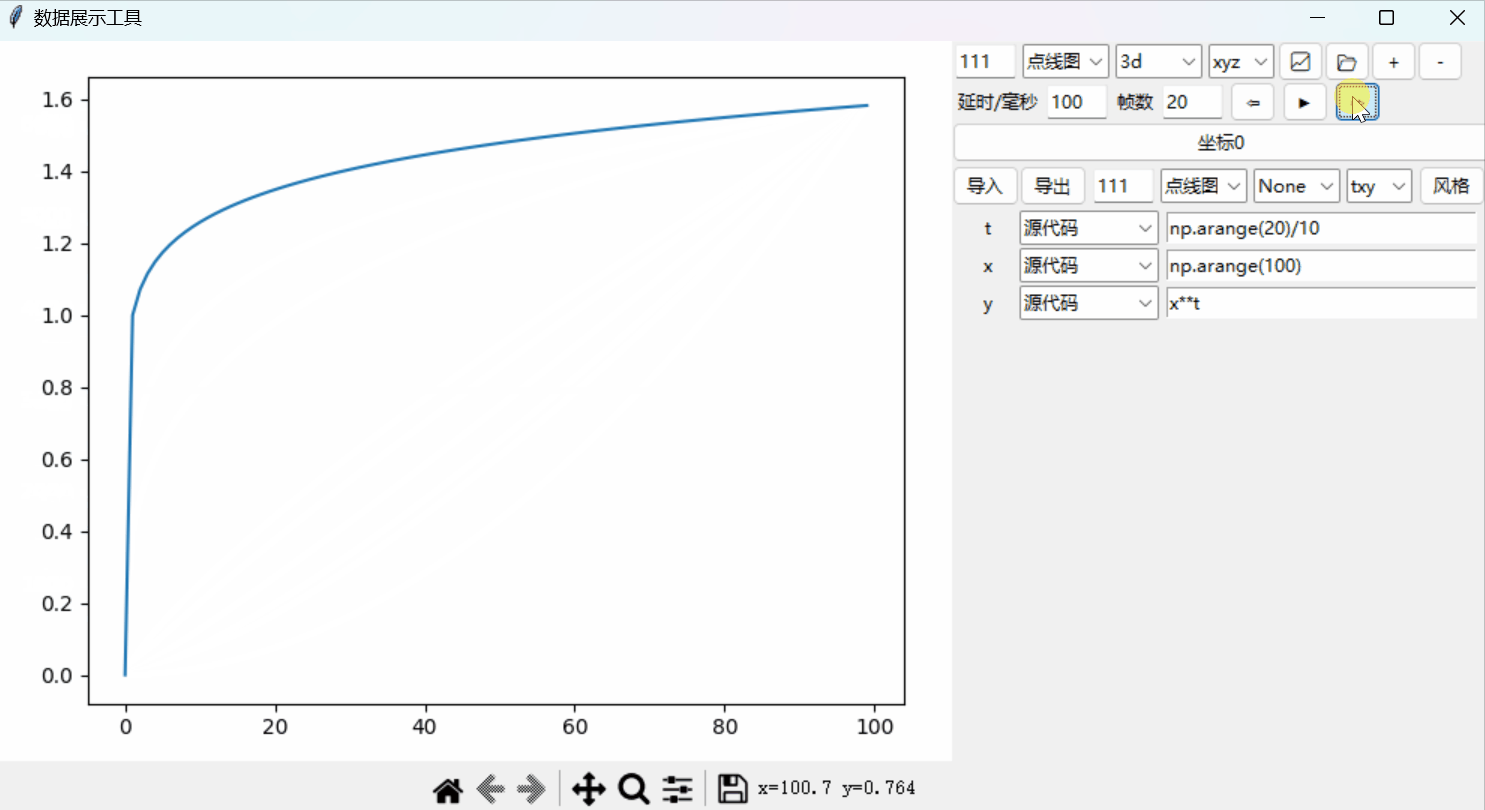
Python绘图系统19:添加时间轴以实现动态绘图
文章目录 时间轴单帧跳转源代码 Python绘图系统: 📈从0开始的3D绘图系统📉一套3D坐标,多个函数📊散点图、极坐标和子图自定义控件:绘图风格📉风格控件📊定制绘图风格坐标设置进阶&a…...
深度解析shell脚本的命令的原理之rm
rm 是 Unix/Linux 系统中的一个基本命令,用于删除文件或目录。以下是对这个命令的深度分析: 基本操作:rm 命令删除一个或多个文件或目录。这是通过从文件系统中移除链接来完成的。在 Unix/Linux 中,文件是通过链接(可以…...
)
RPA机器人流程自动化专题培训大纲(供大家参考使用)
一、RPA机器人流程自动化概述 RPA的定义和发展历程RPA的应用场景和优势RPA与人工智能的关系 二、RPA机器人流程自动化基础知识 RPA的基本原理和技术架构RPA的常用技术和工具RPA的编程语言和开发环境 三、RPA机器人流程自动化实战应用 如何进行业务流程分析与优化如何利用R…...
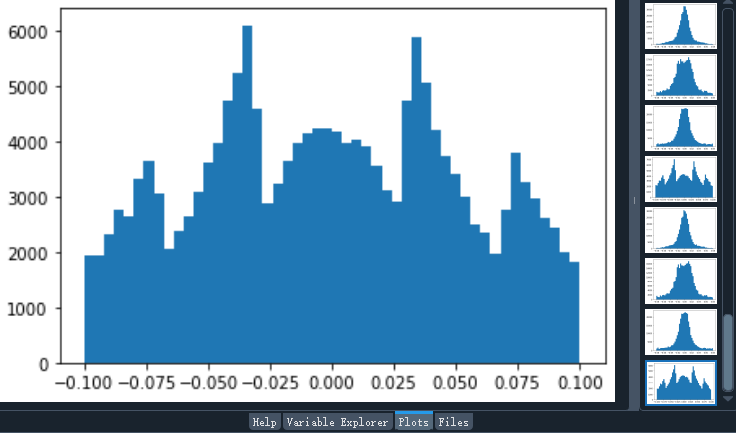
Python用若干列的数据多条件筛选、去除Excel数据并批量绘制直方图
本文介绍基于Python,读取Excel数据,以一列数据的值为标准,对这一列数据处于指定范围的所有行,再用其他几列数据数值,加以筛选与剔除;同时,对筛选与剔除前、后的数据分别绘制若干直方图ÿ…...
驱动开发,IO多路复用实现过程,epoll方式
1.框架图 被称为当前时代最好用的io多路复用方式; 核心操作:一棵树(红黑树)、一张表(内核链表)以及三个接口; 思想:(fd代表文件描述符) epoll要把检测的事件…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...

python打卡day49@浙大疏锦行
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 一、通道注意力模块复习 & CBAM实现 import torch import torch.nn as nnclass CBAM(nn.Module):def __init__…...
