Leetcode 2851. String Transformation
- Leetcode 2851. String Transformation
- 0. 吐槽
- 1. 算法思路
- 1. 整体思路
- 2. 字符串匹配优化
- 2. 代码实现
- 题目链接:2851. String Transformation
0. 吐槽
这道题多少有点坑爹,题目本身挺有意思的,是一道数组题目,其实用数学方法直接可以写出结果的数学表达式,因此做的时候成就感非常强。
但是,坑爹的来了,谁会想到这道题最终卡人的是数组匹配算法,真心晕菜!!!
举个不太恰当的例子,就像是你去复原一个魔方,你想了n久,终于想到了魔方的复原方法,然后到了考场上面,面试官给了你一块木头和一把锯子,让你先做个魔方然后再复原,还限时2h……
就尼玛坑爹啊!!!
不过万幸,总算是搞定了,顺道也优化了一下字符串的匹配算法,虽然非我所愿,但多少也有点成就感吧……
1. 算法思路
1. 整体思路
这一题整体思路上可以视为一道数组题目。
显然的,对于一个长度为 n n n的字符串s,我们经过 k k k此操作之后可能的操作方式总数有 ( n − 1 ) k (n-1)^{k} (n−1)k种。
我们假设第 k k k次操作之后字符串s恰好变为t的操作方式总数为 a k a_k ak,那么显然我们有如下递推公式:
a k = a k − 1 × ( m − 1 ) + ( ( n − 1 ) k − 1 − a k − 1 ) × m = m ⋅ ( n − 1 ) k − 1 − a k − 1 \begin{aligned} a_k &= a_{k-1} \times (m-1) + ((n-1)^{k-1} - a_{k-1}) \times m \\ &= m \cdot (n-1)^{k-1} - a_{k-1} \end{aligned} ak=ak−1×(m−1)+((n−1)k−1−ak−1)×m=m⋅(n−1)k−1−ak−1
其中, m m m表示s的所有循环字符串(至多经过一次操作之后得到的字符串)当中t的个数,亦即,s可以通过 m m m种旋转方式直接变为t。
此时,我们由上述递推公式,不难迭代写出:
a k = m ⋅ ( n − 1 ) k − 1 − a k − 1 a k − 1 = m ⋅ ( n − 1 ) k − 2 − a k − 2 ⋯ a 1 = m ⋅ ( n − 1 ) 0 − a 0 \begin{aligned} a_k &= m \cdot (n-1)^{k-1} - a_{k-1} \\ a_{k-1} &= m \cdot (n-1)^{k-2} - a_{k-2} \\ \cdots \\ a_1 &= m \cdot (n-1)^{0} - a_{0} \end{aligned} akak−1⋯a1=m⋅(n−1)k−1−ak−1=m⋅(n−1)k−2−ak−2=m⋅(n−1)0−a0
我们分别带入之后即可得到 a k a_k ak的表达式如下:
a k = ( − 1 ) k a 0 + m ∑ i = 0 k − 1 ( − 1 ) k − 1 − i ⋅ ( n − 1 ) i = ( − 1 ) k a 0 + m ⋅ ( n − 1 ) k − ( − 1 ) k n \begin{aligned} a_{k} &= (-1)^{k} a_0 + m \sum\limits_{i=0}^{k-1} (-1)^{k-1-i} \cdot (n-1)^i \\ &= (-1)^{k} a_0 + m \cdot \frac{(n-1)^k - (-1)^k}{n} \end{aligned} ak=(−1)ka0+mi=0∑k−1(−1)k−1−i⋅(n−1)i=(−1)ka0+m⋅n(n−1)k−(−1)k
因此,事实上这道题我们可以通过 n , m , k n,m,k n,m,k的值直接算出我们的最终答案。
剩下的问题就是 n , m n,m n,m的求解了,其中 n n n是显然的,剩下的就是 m m m的求解了,本来其实就是将s再拼接一份然后看一下新组成的这个字符串当中t一共出现的次数就行了,用伪代码表示就是:
n = len(s)
ns = s + s[:-1]
m = len([i for i in range(n) if ns[i:i+n] == t])
结果没想到这里居然一直超时,最后这道题大部分的时候居然都集中在了解决这个问题上面,也是醉了……
下面,我们就来看一下我们具体对于这个问题的优化。
2. 字符串匹配优化
如前所述,这里事实上我们可以将问题抽象为如下问题:
已知两个字符串
s和t,问s当中t一共出现过多少次。
因此这里其实就是一个字符串匹配的问题,不过我们可以对其进行一下优化:
- 如果
s当中的某一段已经和t匹配上了(假设起始坐标为i),此时我们就可以通过t本身的特性,找到t当中最接近头部的某个位置idx,满足t[idx:] == t[:n-idx],此时我们可以直接跳转到这个位置,然后比较子串t[n-idx:]与s[i+n:i+n+idx]是否一致即可判断新的这个子串s[i+idx:i+idx+n]是否等于t,而无需判断中间的位置以及完整地判断这两个子串是否相同。
此时,问题就简化到了如何求得t当中最接近头部的某个位置idx,满足t[idx:] == t[:n-idx],而这个可以通过z-algorithm来进行快速实现,关于这部分的内容,我们之前已经写过了一个博客(经典算法:Z算法(z algorithm))对其进行过整理了,这里我们就不再展开赘述了。
2. 代码实现
综上,我们就可以给出我们最终的python代码实现如下:
def z_algorithm(s):n = len(s)z = [0 for _ in range(n)]l, r = -1, -1for i in range(1, n):if i > r:l, r = i, iwhile r < n and s[r-l] == s[r]:r += 1z[i] = r-lr -= 1else:k = i - lif z[k] < r - i + 1:z[i] = z[k]else:l = iwhile r < n and s[r-l] == s[r]:r += 1z[i] = r-lr -= 1z[0] = nreturn zdef find_all(s, t):l, n = len(s), len(t)prefix = z_algorithm(t)nxt, m = n, 0for i in range(1, n):if i + prefix[i] == n:nxt = im = prefix[i]breakidx = 0cnt = 0while idx < l:idx = s.find(t, idx)if idx == -1:breakcnt += 1if nxt < n:while idx+n < l and t[m:] == s[idx+n:idx+n+nxt]:idx = idx+nxtcnt += 1idx += 1return cntclass Solution:def numberOfWays(self, s: str, t: str, k: int) -> int:MOD = 10**9+7n = len(s)m = find_all(s+s[:-1], t)f0 = 0 if s != t else 1fk = f0 * pow(-1, k) + m * pow(n, -1, MOD) * (pow(n-1, k, MOD) - pow(-1, k))return fk % MOD
提交代码评测得到:耗时801ms,占用内存41.1MB。
值得一提的是,截至23.9.10晚间,当前这个执行效率远远高于其他python提交的算法执行效率(其他实现当中最快的执行时间为3167ms),多少也是让我感觉挺有成就感的……
相关文章:

Leetcode 2851. String Transformation
Leetcode 2851. String Transformation 0. 吐槽1. 算法思路 1. 整体思路2. 字符串匹配优化 2. 代码实现 题目链接:2851. String Transformation 0. 吐槽 这道题多少有点坑爹,题目本身挺有意思的,是一道数组题目,其实用数学方法…...

在PHP8中对数组进行计算-PHP8知识详解
在php8中,提供了丰富的计算函数,可以对数组进行计算操作。常见的计算函数如下几个:array_sum()函数、array_merge()函数、array_diff()函数、array_diff_assoc()函数、array_intersect()函数、array_intersect_assoc()函数。 1、array_sum()函…...

Android BottomSheetDialog最大展开高度问题
修改界面的时候遇到了这个问题,这个问题比较简单,网上解决方案也很多,这是 peekHeight 半展开高度,毕竟只是 dialog,全铺满就我们不必考虑 dialog 了 方法是在DialogFragment初始化dialog时处理 companion object {/*** 设置弹窗高度 默认展开无折叠情况 */ const val …...

记录Linux部署人脸修复GFPGAN项目Docker Python 使用
记录Linux 服务器使用人脸修复GFPGAN 项目 1:阿里云安装docker,用docker 是隔离环境,Python环境还真是麻烦… https://help.aliyun.com/zh/ecs/use-cases/deploy-and-use-docker-on-alibaba-cloud-linux-2-instances 2:关于docker 镜像,想找个好的镜像也是很难,百度吧,很多Li…...

如何编写可重入的函数?
编写可重入(reentrant)的函数是在多线程环境或并发编程中非常重要的任务。可重入函数是一种可以安全地被多个线程同时调用的函数,而不会导致数据竞争或不一致性的函数。在C语言中,编写可重入函数需要遵循一些特定的规则和技巧。本…...

使用纯C语言定义通用型数据结构的方法和示例
文章目录 前言以实现优先队列来描述实现思想基本类型的包装类型比较函数演示总结 前言 最近一段时间在复习数据结构和算法,用的C语言,不得不说,不学个高级语言再回头看C语言根本不知道C语言的强大和完美,不过相比之下也有许多不便…...

数据结构基础8:二叉树oj+层序遍历。
二叉树oj层序遍历 题目一:二叉树的销毁:方法一:前序遍历:方法二:后序遍历: 题目二:二叉树查找值为x的节点方法一:方法二:方法三: 题目三:层序遍历…...

Spring注解家族介绍:@RestController
前言: Spring Boot可以说是当前JAVA最为重要的一个框架,而Spring Boot的基石Spring中有着丰富的注解,因此我们会利用几篇文章来讲解我目前学到的各种注解,因此本类型文章的篇幅会比较短,主要着重于介绍各个注解。 目录…...
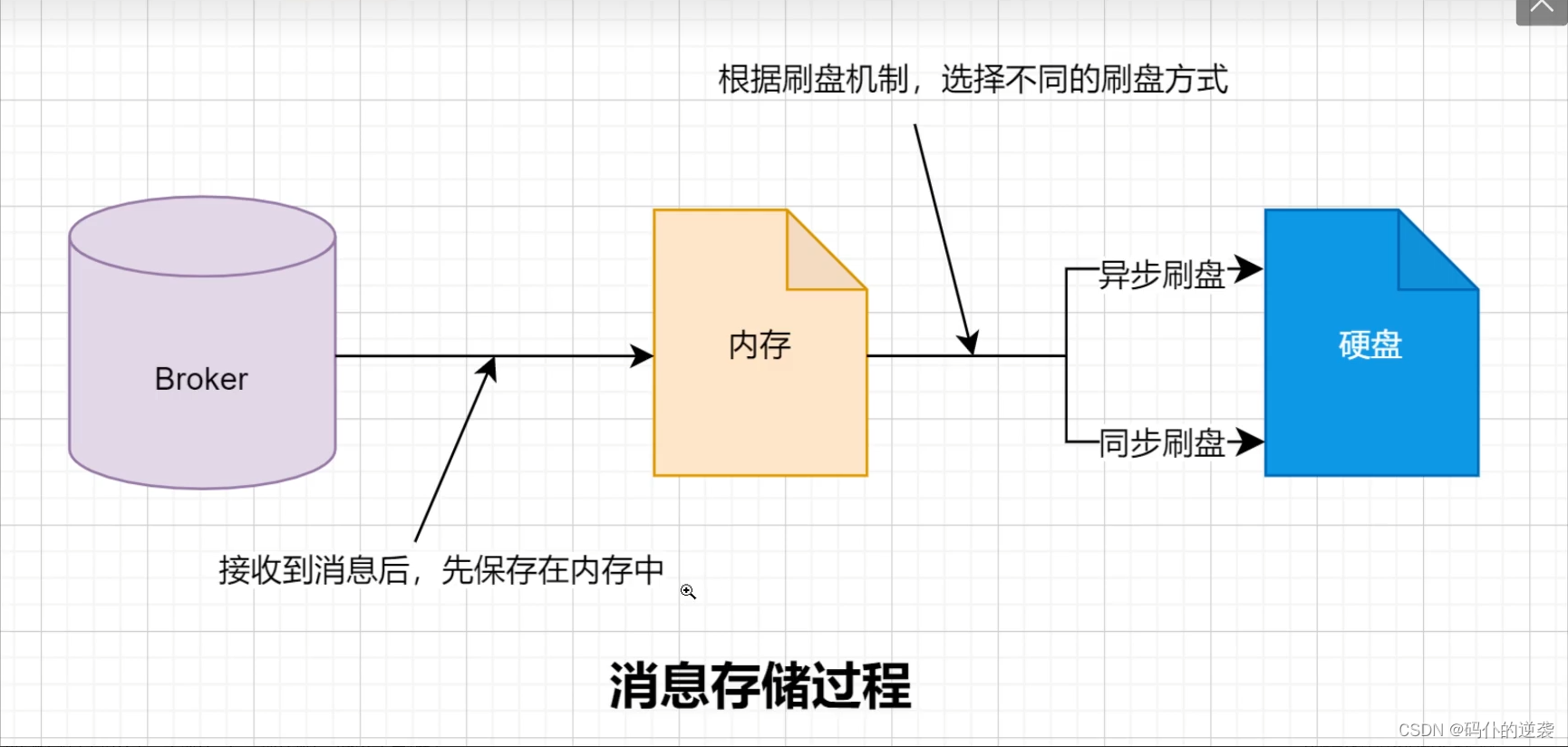
rocketmq
🍓代码仓库 https://gitee.com/xuhx615/rocket-mqdemo.git 🍓基本概念 ⭐生产者(Producer):消息发布者⭐主题(Topic):topic用于标识同一类业务类型的消息⭐消息队列(MessageQueue)…...
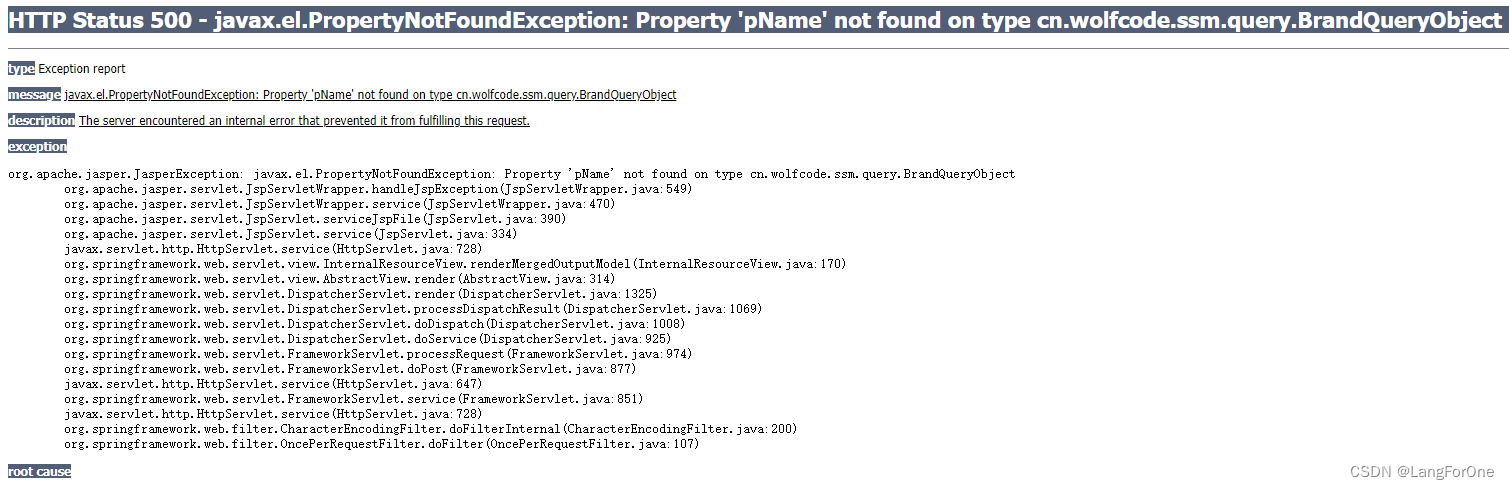
JAVA成员变量首字母小写,第二个字母大写报错问题(原因:Lombok与Spring冲突)
1、问题现象: JAVA类里定义成员变量使用首字母小写,第二个字母大写 Getter Setter public class BrandQueryObject extends QueryObject{private String pName; }结果页面报错,无法找到类型为 cn.wolfcode.ssm.query.BrandQueryObject 的对象…...

Python入门教程 |Python 错误和异常
Python3 错误和异常 作为 Python 初学者,在刚学习 Python 编程时,经常会看到一些报错信息,在前面我们没有提及,这章节我们会专门介绍。 Python 有两种错误很容易辨认:语法错误和异常。 Python assert(断…...

API商品接口对接使用:从理论到实践
随着电子商务的飞速发展,API商品接口已成为现代电子商务应用程序不可或缺的一部分。通过API商品接口,开发者可以轻松地从其他应用程序或服务中获取商品信息,实现快速、高效的电子商务功能。本文将探讨API商品接口的概念、对接使用的方法以及一…...

解决stable diffusion webui1.6 wd1.4 tagger加载失败的问题
由于webui源码的变化,需要修改两个地方的import 1.tagger/ui.py # 第十行 # from webui import wrap_gradio_gpu_call # 原代码 from modules.call_queue import wrap_gradio_gpu_call1.preload.py # 第4行开始 # from modules.shared import models_path # 原…...

Python学习-实现简单的http服务
基于Python实现一个简单的HttpServer,当用户在浏览器中输入IP地址:8000时,则会返回index.html页面内容,访问其它信息,则会返回错误信息(404) """ httpserver v1.0 1.获取来自浏览器的请求, 2.判断如果请求内容是 …...

#循循渐进学51单片机#变量进阶与点阵LED#not.6
1、掌握变量的作用域及存储类别。 局部变量 函数内部声明的变量,只在函数内部有效,在本函数以外是不能使用的,叫局部变量。 全局变量 在函数外部声明的变量就是全局变量,一个源程序可以包含一个或多个函数,全局变量…...

访问者模式
图片转载自 #include<iostream> using namespace std; #include<list> /*模板工厂单例化,所有的商品被注册进工厂中*/ /*访问者模式(行为型模式) 访问者,被访问者 visit accept 让访问变成一种操作,不同…...
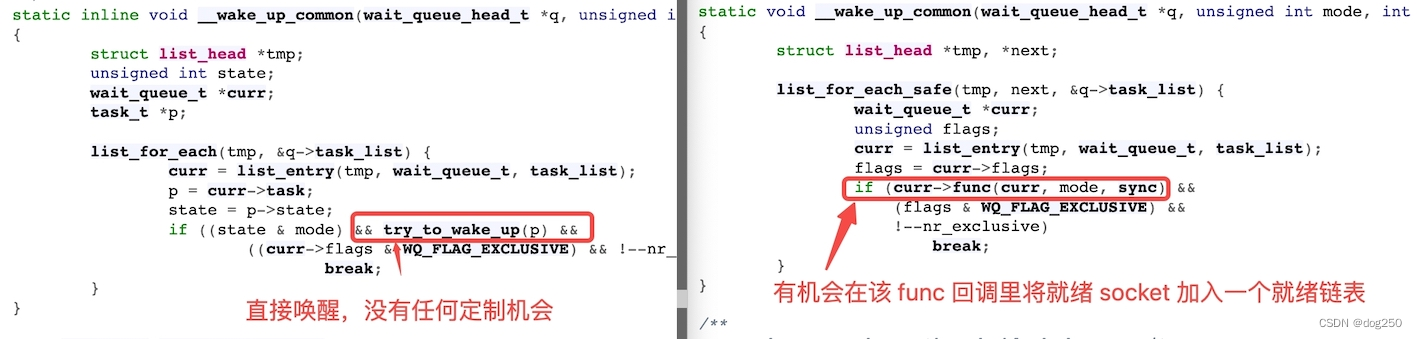
epoll 的实现
epoll 这么好,为什么迟至 2.6 版本的 kernel 才支持(epoll manual: The epoll API was introduced in Linux kernel 2.5.44.)?2.4 版本的 kernel 不支持 epoll? 原因很简单,epoll 没什么神奇的。在早期没有太多的并发连接要处理&…...

怎么用excel管理固定资产
在当今的数字时代,我们已经习惯了使用各种电子工具来提高我们的生产力。其中,Excel无疑是一个强大的工具,它不仅可以帮助我们处理数据,还可以用来进行复杂的计算和分析。然而,你可能不知道的是,Excel也可以…...
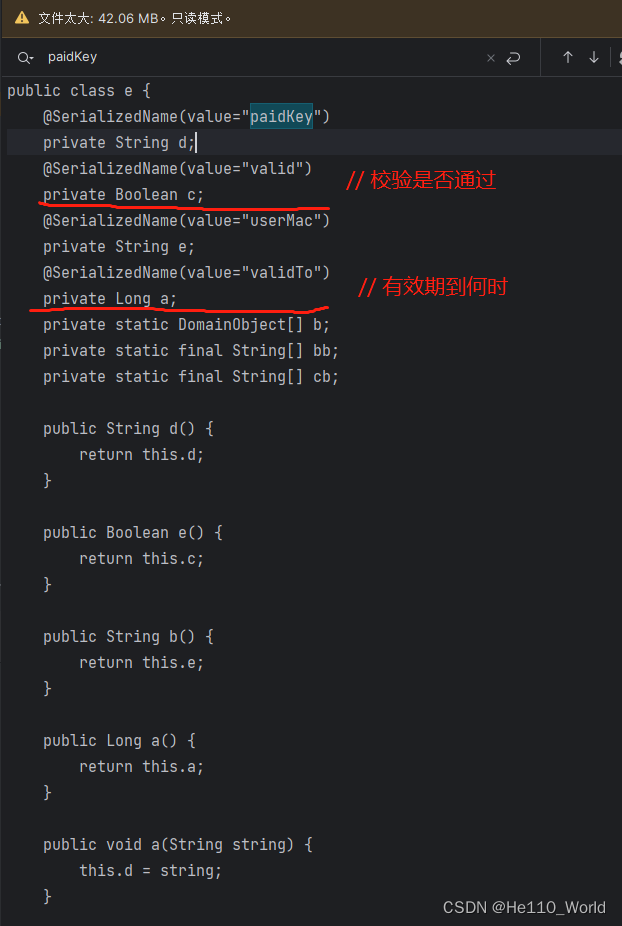
记录crack某IDE插件过程
声明:本文仅记录学习过程,已对关键位置脱敏处理,未提供任何工具,请支持正版。 反编译jar包 使用cfr进行对插件核心jar包MyBxxxxxx-obfuss.jar进行反编译,在本地生成a.txt。 java -jar cfr-0.152.jar MyBxxxx-obfuss.…...

Android DEX相关,ART加载OAT文件
android .dex文件,对于Android DEX文件详细说明 Android dex、odex、oat、vdex、art区别 Android下的DEX文件和SO文件梳理总结 Android[art]-Android dex,odex,oat,vdex,art文件结构学习总结 第四章 常见的 Android 文件格式&…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
