动态规划:子序列问题(C++)
动态规划:子序列问题
- 前言
- 子序列问题
- 1.最长递增子序列(中等)
- 2.摆动序列(中等)
- 3.最长递增子序列的个数(中等)
- 4.最长数对链(中等)
- 5.最长定差子序列(中等)
- 6.最长的斐波那契子序列的长度(中等)
- 7.最长等差序列(中等)
- 8.等差数列划分II - 子序列(困难)
前言
动态规划往期文章:
- 动态规划入门:斐波那契数列模型以及多状态
- 动态规划:路径和子数组问题
子序列问题
1.最长递增子序列(中等)
链接:最长递增子序列
-
题目描述

-
做题步骤
-
状态表示
对于线性dp,我们通常采用下面两种表示:
(1)以某个位置为结尾,……
(2)以某个位置为起点,……
这两种方式我们通常采用第一种,以某个位置为结尾,再结合题目要求,我们可以定义状态表示为dp[i]:以i位置为结尾的所有子序列中,最长递增子序列的长度。 -
状态转移方程
对于以i位置为结尾的子序列,一共有两种可能:
(1)不接在别人后面,就自己一个,dp[i] = 1
(2)接在[0,1,2,……,i - 1]这些位置后面,设0 <= j <= i - 1,能保持子序列递增(nums[j] < nums[i])就可以接在该位置后面。
从0~i - 1枚举j,看接在那个位置后面长度最大:
即dp[i] = max(dp[i], dp[j] + 1) -
初始化
每个位置最小都为1,全都初始化为1。 -
填表顺序
保证填当前状态时,所需状态已经计算过,填表顺序为从左往右。 -
返回值
没法直接确定最长子序列的结尾位置,一边dp一边更新最大值。
- 代码实现
class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();//dp[i]表示以i位置为结尾的最长递增子序列vector<int> dp(n, 1); int ret = 1;for(int i = 1; i < n; i++){//从[0, i-1]看一圈,找接在那个符合条件的位置后面可以让子序列最长for(int j = 0; j < i; j++) if(nums[j] < nums[i])dp[i] = max(dp[i], dp[j] + 1); //看看能不能更新最大ret = max(ret, dp[i]);}return ret;//时间复杂度:O(N ^ 2)//空间复杂度:O(N)}
};
2.摆动序列(中等)
链接:摆动序列
-
题目描述

-
做题步骤
-
状态表示
依据前面的经验,我们依据可以定义状态表示为dp[i]:以i位置为结尾的所有摆动序列中的最大长度。 -
状态转移方程
对于长度大于1的摆动序列,其有两种情况:
(1)处于上升状态,比如(1, 7, 4, 9)。
(2)处于下降状态,比如(1, 17, 10)。
因此我们需要同时记录两种状态,其中f[i]表示以i位置为结尾并处于上升状态的最长摆动序列长度,g[i]表示处于下降状态。
摆动序列分析完了,我们再来分析单个位置,一共有两种可能:
(1)不接在别人后面,自己玩,dp[i] = 1
(2)接在[0,1,2,……,i - 1]这些位置后面,设0 <= j <= i - 1。
①如果接在j位置后处于上升状态(nums[i] - nums[j] > 0),需要以j位置为结尾并处于下降状态的状态,即f[i] = g[j] + 1。
②如果接在j位置后处于下降状态(nums[i] - nums[j] < 0),需要以j位置为结尾并处于上升状态的状态,即g[i] = f[j] + 1。 -
初始化
序列长度最小为1,所有位置全都初始化为1。 -
填表顺序
保证填当前状态时,所需状态已经计算过,填表顺序为从左往右。 -
返回值
没法直接确定最长摆动序列的结尾,所以一边dp一边更新最大值。
- 代码实现
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {//dp[i]表示以i位置为结尾的最长摆动序列长度int n = nums.size();vector<int> f(n, 1);//处于上升状态vector<int> g(n, 1); //处于下降状态int ret = f[0]; //记录最终结果for(int i = 1; i < n; i++){for(int j = 0; j < i; j++){int gap = nums[i] - nums[j];//处于上升if(gap > 0)f[i] = max(f[i], g[j] + 1);//处于下降else if(gap < 0)g[i] = max(g[i], f[j] + 1);//相同的情况为1不用处理}ret = max({ret, f[i], g[i]});}return ret;//时间复杂度:O(N ^ 2)//空间复杂度:O(N)}
};
3.最长递增子序列的个数(中等)
链接:最长递增子序列的个数
-
题目描述

-
做题步骤
-
状态表示
依据前面的经验,我们可以定义状态表示dp[i]:以i位置为结尾的最长递增子序列个数。 -
状态转移方程
要更新当前位置的最长递增子序列个数,无非是看接在那几个位置后面长度最大,但问题就在于现在只有前面位置的序列个数,没有长度,所以我们需要再加一个表来记录长度:
(1)count[i]:以i位置为结尾的最长递增子序列个数
(2)len[i]:以i位置为结尾的最长递增子序列长度
len[i]前面已经讲过,我们分析count[i]:
(1)不接在别人后面,最大长度就为1,count[i] = 1
(2)接在[0,1,2,……,i - 1]这些位置后面,设0 <= j <= i - 1,能保持子序列递增(nums[j] < nums[i])就可以接在该位置后面。
从0~i - 1枚举j,依据接在那个位置后面的长度进行分析:
①比原来长度小(len[i] > len[j] + 1),不用管。
②比原来长度大(len[i] < len[j] + 1),原来的序列个数无论多少都必须狠狠切割了,个数更新为更长的,即count[i] = count[j]。
③和原来长度一样(len[i] == len[j] + 1),计数增加,即count[i] += count[j]。 -
初始化
序列长度最小为1,全都初始化为1。 -
填表顺序
保证填当前状态时,所需状态已经计算过,填表顺序为从左往右。 -
返回值
(1)完成了前面的工作,我们知道以每一个位置为结尾的最长递增子序列长度和个数,但是并不知道以那几个位置为结尾的序列最长,所以我们需要一边dp一边更新最大长度max_length。
(2)知道了最大长度,我们只需要遍历一次count表,把长度为max_length的序列统计出来即可。
- 代码实现
class Solution {
public:int findNumberOfLIS(vector<int>& nums) {int n = nums.size();vector<int> count(n, 1); //f[i]表示以i位置为结尾的最长子序列个数auto len = count; //g[i]表示以i位置为结尾的最长递增子序列长度int max_length = len[0];for(int i = 1; i < n; i++){for(int j = 0; j < i; j++){if(nums[i] > nums[j]){//找到了更加长的if(len[i] < len[j] + 1){len[i] = len[j] + 1;count[i] = count[j];}else if(len[i] == len[j] + 1) //长度相同 count[i] += count[j]; }}max_length = max(max_length, len[i]);}int ret = 0; //返回值//遍历一次,计算最长序列个数for(int i = 0; i < n; i++) if(len[i] == max_length)ret += count[i];return ret;//时间复杂度:O(N ^ 2)//空间复杂度:O(N)}
};
4.最长数对链(中等)
链接:最长数对链
-
题目描述

-
做题步骤
-
状态表示
依据前面经验,我们定义状态表示dp[i]:以i位置为结尾最长数对链长度。 -
状态转移方程
这个题目的分析其实和前面的最长递增子序列基本一致。
(1)不接在别人后面,自己玩,dp[i] = 1
(2)接在[0,1,2,……,i - 1]这些位置后面,设0 <= j <= i - 1,满足数对链要求(pairs[j][1] < pairs[i][0])就可以接在该位置后面。
从0~i - 1枚举j,看接在那个位置后面长度最大:
即dp[i] = max(dp[i], dp[j] + 1) -
初始化
长度最小为1,全都初始化为1。 -
填表顺序
保证填当前状态时,所需状态已经计算过,填表顺序为从左往右。 -
返回值
没法直接确定最长数对链的结尾,所以一边dp一边更新最大值。
- 代码实现
class Solution {
public:int findLongestChain(vector<vector<int>>& pairs) { sort(pairs.begin(), pairs.end()); //先排序int n = pairs.size();//dp[i]表示以i位置为终点的最长长度vector<int> dp(n, 1);int ret = 1; //记录最长for(int i = 1; i < n; i++){for(int j = 0; j < i; j++) if(pairs[j][1] < pairs[i][0]) //如果可以接在后面 dp[i] = max(dp[i], dp[j] + 1); ret = max(ret, dp[i]);}return ret;//时间复杂度:O(N ^ 2)//空间复杂度:O(N)}
};
5.最长定差子序列(中等)
链接:最长定差子序列
-
题目描述

-
做题步骤
-
状态表示
依据前面的经验,我们定义状态表示dp[i]:以下标i位置为结尾的最长等差子序列长度。 -
状态转移方程
这个题目最好想的做法就是递增子序列的做法,但这样写会超时,我们可以分析一下原因:
(1)递增子序列可以接在很多位置的后面。
(2)等差子序列只能接在固定的位置后面,比如(1, 2, 3, 4),difference为1,里面的4只能接在3后面,其它的判断都是多余的。
那我们就换一种思路,还是(1, 2, 3, 4),difference为1这个例子,我们在填4位置的时候,如果能够直接找到以3(arr[i] - difference)为结尾的最长递增子序列就好了。
我们可以把元素arr[i]与dp[i]绑定,创建一个哈希表hash,我们可以直接在这个哈希表中做动态规划,那状态转移方程就为:
hash[i] = hash[arr[i] - difference] + 1。 -
初始化
在填表的时候,如果前置状态不存在,我们不单独处理(0加1变成1刚好对应自己一个的情况)。因此我们只需要把第⼀个元素放进哈希表中, hash[arr[0]] = 1即可。 -
填表顺序
保证填当前状态时,所需状态已经计算过,填表顺序为从左往右。 -
返回值
不确定最长等差子序列的结尾,所以一边dp一边更新最大值。
- 代码实现
class Solution
{public:int longestSubsequence(vector<int>& arr, int difference) {// 创建⼀个哈希表unordered_map<int, int> hash; // {arr[i], dp[i]}hash[arr[0]] = 1; // 初始化int ret = 1;for(int i = 1; i < arr.size(); i++){hash[arr[i]] = hash[arr[i] - difference] + 1;ret = max(ret, hash[arr[i]]);}return ret;//时间复杂度:O(N)//空间复杂度:O(N)}
};
6.最长的斐波那契子序列的长度(中等)
链接:最长的斐波那契子序列的长度
-
题目描述

-
做题步骤
-
状态表示
依据经验我们可能会定义状态表示为以i位置为结尾的最长斐波那契序列的长度,但这样定义有一个致命的问题:不知道接在某一个位置后能否构成斐波那契序列。
一个元素无法确定,但如果我们知道斐波那契序列的后两个元素,我们就可以推导出前一个元素,从而解决前面的问题。
所以定义一个二维表dp[i][j]:以i,j位置为后两个元素的最长斐波那契序列的长度。 -
状态转移方程
规定 i 比 j 小,其中j从[2, n - 1]开始枚举,i从[1, j - 1]开始枚举。
设 nums[i] = b, nums[j] = c ,那么这个序列的前⼀个元素就是 a = c - b ,我们根据 a 的情况讨论:
(1)a存在,设其下标为k,并且 a < b,这个时候c可以接在以a、b为结尾的斐波那契序列后面,则dp[i][j] = dp[k][i] + 1。
(2)a存在,但是 b < a < c,这个时候只能b和c两个自己构成,dp[i][j] = 2。
(3)a不存在,这个时候只能b和c两个自己构成,dp[i][j] = 2。
我们发现,在状态转移⽅程中,我们需要确定 a 元素的下标。因此我们可以在 dp 之前,将所有的「元素 + 下标」绑定在⼀起,放到哈希表中。 -
初始化
长度最小为2,全都初始化为2。 -
填表顺序
固定最后一个数,枚举倒数第二个数。 -
返回值
不确定最长斐波那契子序列的结尾,所以一边dp一边更新最大值。
- 代码实现
class Solution {
public: int lenLongestFibSubseq(vector<int>& arr){int n = arr.size();//i->jdp[i][j]表示以i,j为后两个的斐波那契数列最长长度vector<vector<int>> dp(n, vector<int>(n, 2));unordered_map<int, int> hash;for(int i = 0; i < n; i++) hash[arr[i]] = i;int ret = 2;for (int j = 2; j < n; j++){for (int i = 1; i < j; i++){int former = arr[j] - arr[i];//a b c,a < b 并且a存在if (former < arr[i] && hash.count(former)){dp[i][j] = dp[hash[former]][i] + 1;}ret = max(ret, dp[i][j]);}}//斐波那契序列最小为3,为2的情况返回0return ret > 2 ? ret : 0;//时间复杂度:O(N)//空间复杂度:O(N ^ 2)}
};
7.最长等差序列(中等)
链接:最长等差序列
-
题目描述

-
做题步骤
-
状态表示
和前面一道题类似,只有一个元素无法确定等差序列的样子,我们需要有后面两个元素才能确定,故定义一个二维表dp[i][j]:以i,j为后两个元素的最长等差子序列的长度。 -
状态转移方程
规定 i 比 j 小,设 nums[i] = b, nums[j] = c ,那么这个序列的前⼀个元素就是 a = 2 * nums[i] - nums[j] (等差序列的性质捏) ,我们根据 a 的情况讨论:
(1)a存在,设其下标为k,这个时候c可以接在以a、b为结尾的序列后面,则dp[i][j] = dp[k][i] + 1。
(2)a不存在,这个时候只能b和c两个自己构成,dp[i][j] = 2。
我们发现,在状态转移方程中,我们需要确定 a 元素的下标。因此我们可以将所有的「元素 + 下标」绑定在⼀起,放到哈希表中。对于这个题目哈希表有两种方案:
(1)在dp前就直接放入哈希表,可能出现重复的元素(这个题目是乱序的,前面一题严格递增),要记录这些重复元素,需要让它们的下标形成一个数组,填表前要先遍历数组找到需要的下标,时间消耗很大,这个方案通过不了。
(2)只能采取一边dp一边存入哈希表的方式,在i位置使用完后存入哈希表中,但填表顺序必须固定倒数第二,枚举倒数第一,不能采用上一题固定倒一,枚举倒二的填表方式。我们看这个例子:【0,2,4,4,4,6,8,4,9,4,4】,最后一个4固定,第一个4为倒数第二时,应该去找之前4的下标(这里前面是[0,2],没有4,意味着这个数不应该在哈希表中,但固定倒一,枚举倒二的填表方式使得哈希表中是有保存的,这个时候就完全乱了) -
初始化
长度最小为2,全部初始化为2。 -
填表顺序
填表顺序为固定倒数第二,枚举倒数第一。 -
返回值
不确定最长等差序列的结尾,所以一边dp一边更新最大值。
- 代码实现
class Solution {
public://dp[i][j]表示以i,j为结尾的最长等差数列长度int longestArithSeqLength(vector<int>& nums) {int n = nums.size();unordered_map<int, int> hash; hash[nums[0]] = 0;vector<vector<int>> dp(n, vector<int>(n, 2));int ret = 2;for (int i = 1; i < n; i++) //倒数第二个{for (int j = i + 1; j < n; j++){int former = 2 * nums[i] - nums[j];if (hash.count(former))dp[i][j] = dp[hash[former]][i] + 1;ret = max(ret, dp[i][j]);}hash[nums[i]] = i;}return ret;//时间复杂度:O(N ^ 2)//空间复杂度:O(N ^ 2)}
};
8.等差数列划分II - 子序列(困难)
链接:等差数列划分II - 子序列
-
题目描述

-
做题步骤
-
状态表示
和前面一道题一致,只有一个元素无法确定等差序列的样子,我们需要有后面两个元素才能确定,故定义一个二维表dp[i][j]:以i,j为后两个元素的等差子序列个数。 -
状态转移方程
首先,这个题目不存在重复的等差子序列,只要组成的元素位置不同就视为不同子序列,比如[7,7,7,7,7]这个数组等差子序列个数高达16个。
规定 i 比 j 小,设 nums[i] = b, nums[j] = c ,那么这个序列的前⼀个元素就是 a = 2 * nums[i] - nums[j] ,我们根据 a 的情况讨论:
(1)a存在,这个时候c可以接在以a、b为结尾的序列后面。设a下标为k,这里下标情况就和前面不同了,因为可能存在多个a,我们需要用一个下标数组来记录不同位置的a下标,当k < i时(a在i的前面),dp[i][j] += dp[k][i] + 1,这里的+1表示[a,b,c]这一组,把满足条件的a全部加起来即可。
(2)a不存在,这个时候只能b和c两个自己构成,dp[i][j] = 2。
我们发现,在状态转移方程中,我们需要确定 a 元素的下标。因此我们可以将所有的「元素 + 下标数组」绑定在⼀起,放到哈希表中。 -
初始化
无需初始化,默认为0。 -
填表顺序
填表顺序为固定倒一,枚举倒二。 -
返回值
定义变量sum,一边dp一边累加。
- 代码实现
class Solution {
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();//dp[i][j]表示以i,j为结尾的等差数列个数,规定j > i//前置可能有存在多个,需要一一加起来vector<vector<int>> dp(n, vector<int>(n));unordered_map<long long, vector<int>> hash; //数据和下标数组绑定for(int i = 0; i < n; i++)hash[nums[i]].push_back(i);int sum = 0;for(int j = 2; j < n; j++){for(int i = 1; i < j; i++){long long former = (long long)nums[i] * 2 - nums[j]; //处理数据溢出if(hash.count(former)){for(auto k : hash[former]){//former必须在左边if(k < i)dp[i][j] += dp[k][i] + 1; //这里的1表示[a,b,c]单独一组else //当前a下标不满足,后面的也一定不满足,可以直接跳出break;} }sum += dp[i][j];}}return sum;//相同数据不多的情况下//时间复杂度:O(N ^ 2)//空间复杂度:O(N ^ 2)}
};
相关文章:

动态规划:子序列问题(C++)
动态规划:子序列问题 前言子序列问题1.最长递增子序列(中等)2.摆动序列(中等)3.最长递增子序列的个数(中等)4.最长数对链(中等)5.最长定差子序列(中等&#x…...
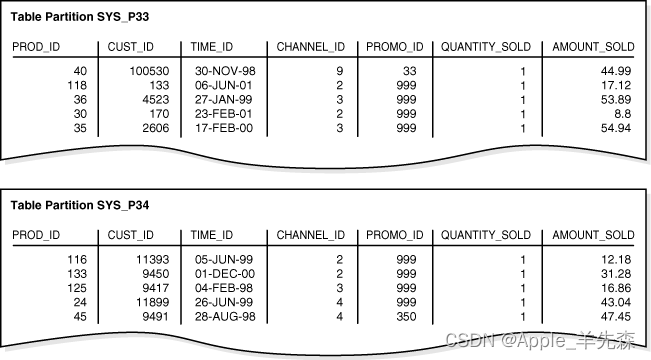
ORACLE的分区(一)
目录 一、分区概念 二、表分区的优点 三、分区策略 一、分区概念 随着时间的发展,一个表的数据会越来越多,当数据量增大的时候我们一般采取建立索引优化索引的方式提高查询速度,但是数据量再次增大即使是索引也无法提高速度,这时…...
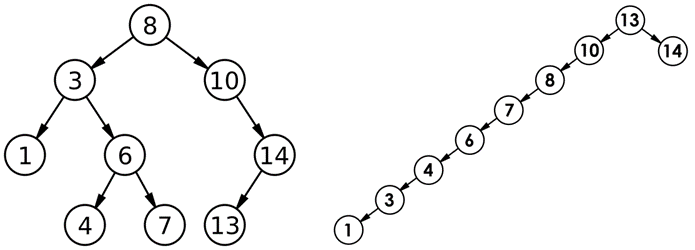
【数据结构】C++实现二叉搜索树
二叉搜索树的概念 二叉搜索树又称为二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树: 若它的左子树不为空,则左子树上所有结点的值都小于根结点的值。若它的右子树不为空,则右子树上所有结点的值都大于根结…...

Python中Mock和Patch的区别
前言: 嗨喽~大家好呀,这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 在测试并行开发(TPD)中,代码开发是第一位的。 尽管如此,我们还是要写出开发的测试,…...
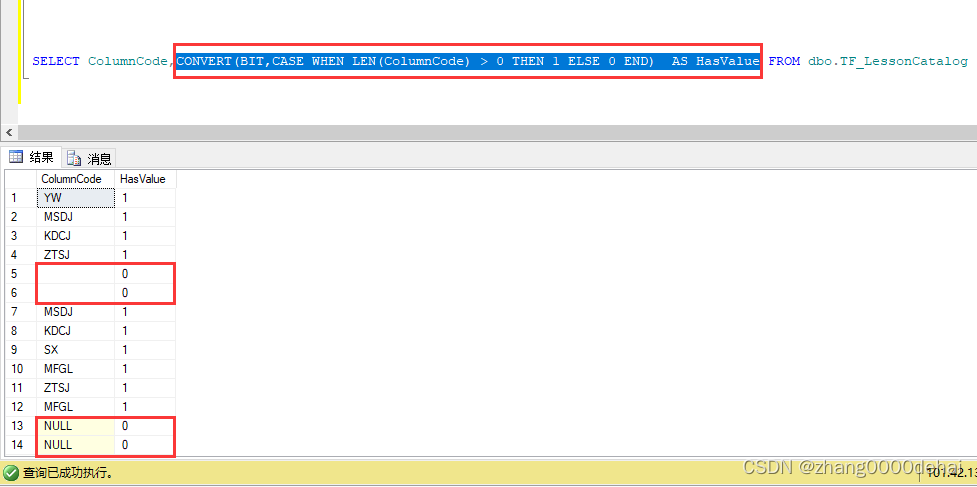
sql server 查询某个字段是否有值 返回bool类型
sql server 查询某个字段是否有值 返回bool类型,true 或 false SELECT ColumnCode,CONVERT(BIT,CASE WHEN LEN(ColumnCode) > 0 THEN 1 ELSE 0 END) AS HasValue FROM dbo.TF_LessonCatalog...

紫光展锐5G芯T820 解锁全新应用场景,让机器人更智能
数字经济的持续发展正推动机器人产业成为风口赛道。工信部数据显示,2023年上半年,我国工业机器人产量达22.2万套,同比增长5.4%;服务机器人产量为353万套,同比增长9.6%。 作为国内商用服务机器人领先企业,云…...

秋招前端面试题总结
1、this指向问题,以前总是迷糊,现在总算是一知半解了。应当遵循以下原则,应该就能做对题目了。 如果一个标准函数,也就是非箭头函数,作为某个对象的方法被调用时,那么这个this指向的就是这个对象。涉及到闭…...

【入门篇】ClickHouse 数据类型
文章目录 1. 引言2. ClickHouse 数据类型2.1 基本数据类型2.1.1 整型2.1.2 浮点型2.1.3 字符串型 2.2 复合数据类型2.2.1 数组2.2.2 枚举类型2.2.3 元组2.2.4 Map2.2.5 Nullable 2.3 特殊数据类型2.3.1 日期和时间类型2.3.2 UUID2.3.3 IP 地址2.3.4 AggregateFunction 2.4 数据…...

关于Python数据分析,这里有一条高效的学习路径
无处不在的数据分析 谷歌的数据分析可以预测一个地区即将爆发的流感,从而进行针对性的预防;淘宝可以根据你浏览和消费的数据进行分析,为你精准推荐商品;口碑极好的网易云音乐,通过其相似性算法,为不同的人…...

基于 json-server 工具,模拟实现后端接口服务环境
文章目录 本地配置后端接口一、安装json-server1、安装 JSON 服务器 安装 JSON 服务器2、创建一个db.json包含一些数据的文件(重点)3、启动 JSON 服务器 启动 JSON 服务器4、现在如果你访问http://localhost:3000/posts/1,你会得到 本地配置后…...

想要精通算法和SQL的成长之路 - 课程表II
想要精通算法和SQL的成长之路 - 课程表 前言一. 课程表II (拓扑排序)1.1 拓扑排序1.2 题解 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 课程表II (拓扑排序) 原题链接 1.1 拓扑排序 核心知识: 拓扑排序是专…...
【sgGoogleTranslate】自定义组件:基于Vue.js用谷歌Google Translate翻译插件实现网站多国语言开发
sgGoogleTranslate源码 <template><div :id"$options.name"> </div> </template> <script> export default {name: "sgGoogleTranslate",props: ["languages", "currentLanguage"],data() {return {//…...
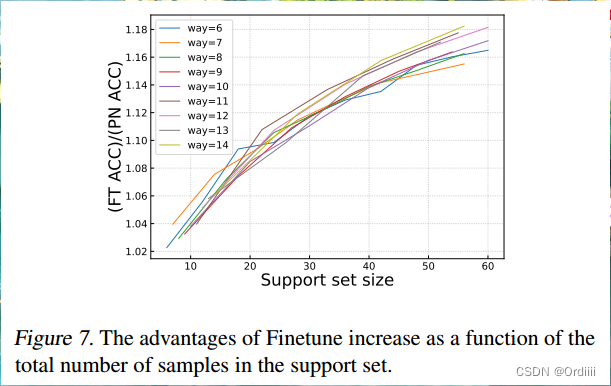
论文总结《A Closer Look at Few-shot Classification Again》
原文链接 A Closer Look at Few-shot Classification Again 摘要 这篇文章主要探讨了在少样本图像分类问题中,training algorithm 和 adaptation algorithm的相关性问题。给出了training algorithm和adaptation algorithm是完全不想关的,这意味着我们…...
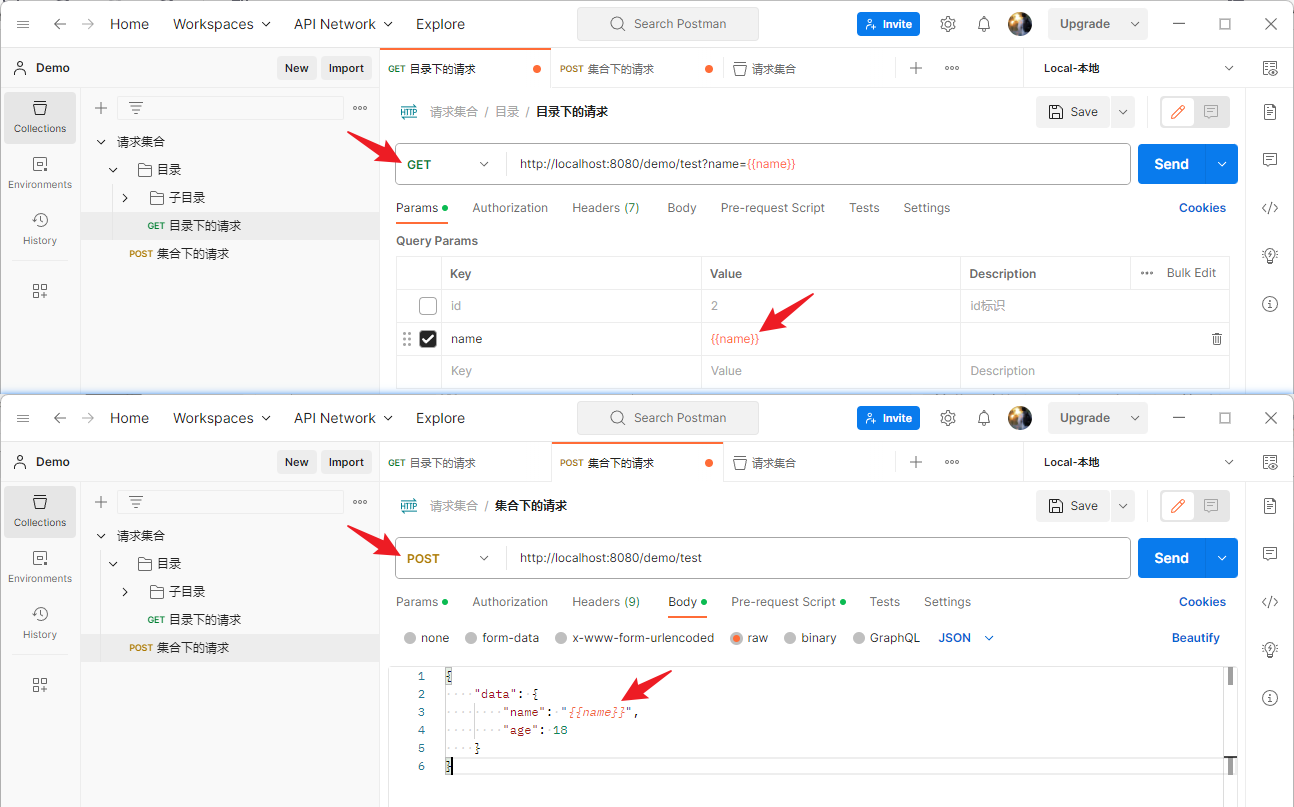
Postman使用_参数设置和获取
文章目录 参数引用内置动态参数手动添加参数脚本设置参数脚本获取参数 参数就像变量一样,它可以是固定的值,也可以是变化的值,比如:会根据一些条件或其他参数进行变化。我们如果要使用该参数就需要引用它。 参数引用 引用动态参数…...

【SQL】优化SQL查询方法
优化SQK查询 一、避免全表扫描 1、where条件中少使用! 或 <>操作符,引擎会放弃索引,进行全表扫描 2、in \or ,用between 或 exist 代替in 3、where 对字段进行为空判断 4、where like ‘%条件’ 前置百分号 5、where …...

Linux-相关操作
2.2.2 Linux目录结构 /:根目录,一般根目录下只存放目录,在Linux下有且只有一个根目录。所有的东西都是从这里开始。当你在终端里输入“/home”,你其实是在告诉电脑,先从/(根目录)开始…...
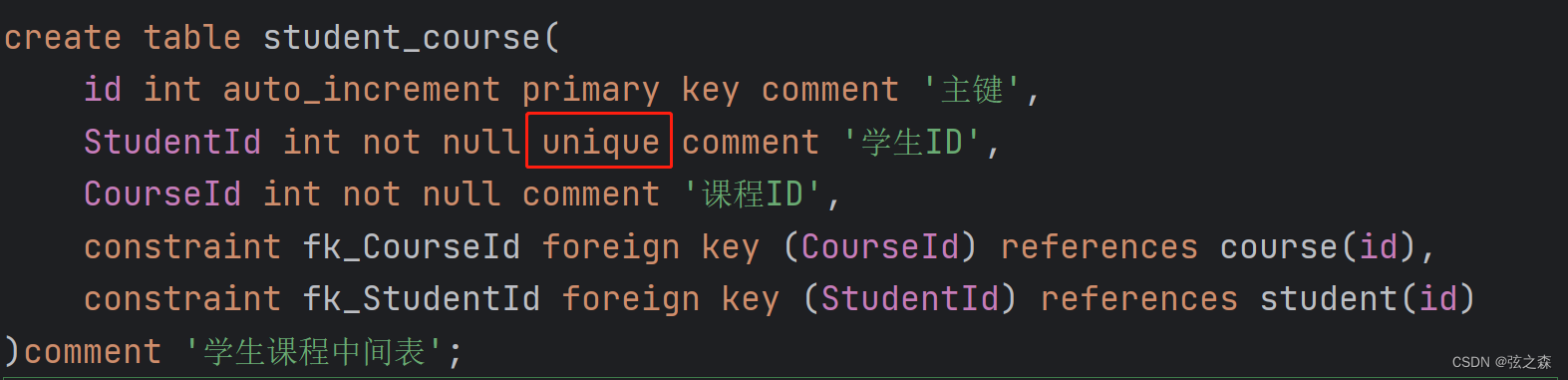
二十、MySQL多表关系
1、概述 在项目开发中,在进行数据库表结构设计时,会根据业务需求以及业务模块之间的关系,分析并设计表结构,由于业务之间相互关联,所以各个表结构之间也存在着各种对应关系 2、多表关系分类 (1࿰…...
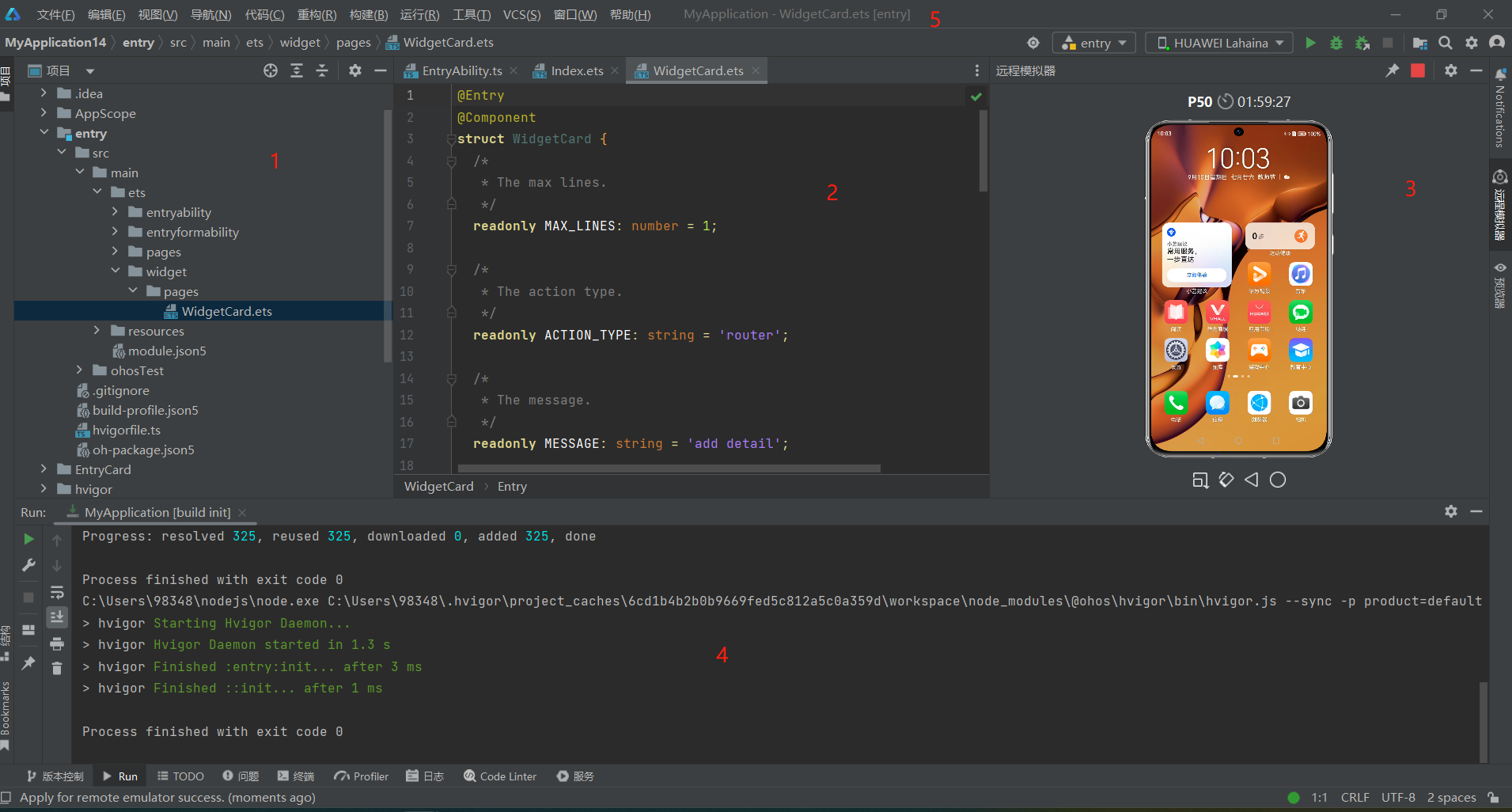
HarmonyOS/OpenHarmony应用开发-DevEco Studio新建项目的整体说明
一、文件-新建-新建项目 二、传统应用形态与IDE自带的模板可供选用与免安装的元服与IDE中自带模板的选择 三、以元服务,远程模拟器为例说明IDE整体结构 1区是工程目录结构,是最基本的配置与开发路径等的认知。 2区是代码开发与修改区,是开发…...
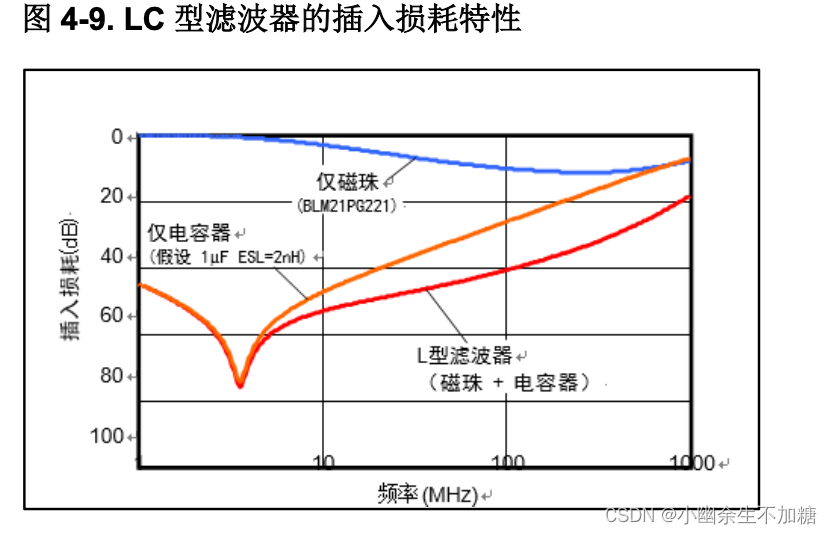
去耦电路设计应用指南(三)磁珠/电感的噪声抑制
(三)磁珠/电感的噪声抑制 1. 电感1.1 电感频率特性 2. 铁氧体磁珠3. LC 型和 PI 型滤波 当去耦电容器不足以抑制电源噪声时,电感器&磁珠/ LC 滤波器的结合使用是很有效的。扼流线圈与铁氧体磁珠 是用于电源去耦电路很常见的电感器。 1. …...

Spring Bean的获取方式
参考https://juejin.cn/post/7251780545972994108?searchId2023091105493913AF7C1E3479BB943C80#heading-12 记录并补充 1.通过BeanFactoryAware package com.toryxu.demo1.beans;import org.springframework.beans.BeansException; import org.springframework.beans.facto…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
