任意区域的色彩一致性处理方法
影像任意感兴趣区域的色彩一致性处理方法,主要是针对掩膜后的影像,类似下图,对非背景区域的像素进行处理 其中非黑色部分我们叫待匀色区域。

这种处理 对于wallis 和直方图匹配 很容易实现,但是颜色转移就相对而言 困难点。
颜色转移技术介绍
颜色转移的目的在于使得参考影像和待处理影像的RGB三维数据点簇形状和位置相匹配。

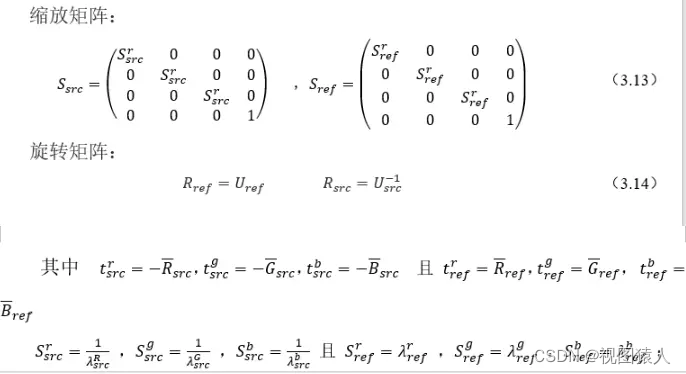
注意: 矩阵级联的时候 实际的效果是从右到左出现的。
任意区域的颜色转移
像素值为255的区域代表前景区域,即为待匀色区域;
步骤①将掩膜后的原始图像转为矩阵rgbs,选定的参考图像转为矩阵rgbt;
rgbs矩阵转换的规则:
创建一个3行M列的矩阵rgbs,其中M是原始图像的总像素个数,矩阵中初始元素值为0。矩阵行数为3,代表掩膜后原始图像的RGB三分量。
矩阵第一行代表R分量 行列数记为a行b列 把R分量的像素值 从第一列的a个像素先填充进rgbs的第一行,然后第二列从上到下继续填充 直到把所有像素填到rgbs的第一行中 G分量和B分量也按照这个规则填充到第二行和第三行中 。rgbt的转换也是一样
这一步我们要将待匀色区域的像素值 存储到矩阵中 也就是说 我们把这个矩阵拿出来 变成三维数据点簇以后进行旋转平移缩放操作 把它变成和ref一样的三维点簇 变好之后 把这个矩阵再按照顺序填充回原单位
就是说 原来待匀色区域的每个像素 我们经过挑选把它选出来 变为整体然后调整它的值之后 再把它放回原来的单位。 很像一个场景 从很多人里面选择一部分人出来 然后训练他们,他们的能力值改变以后,把每个人遣送回原单位,ok。 所以主要就是三个过程:怎么选出来 怎么训练 怎么放回去 所以就按照这三个步骤写下面的文章
怎么选:上面已经把要处理的图像(前景+背景)和ref图像转为 矩阵了 (之所以这么转矩阵 是迎合matlab里api的矩阵转换规则)
步骤②:将要处理的图像中待匀色区域像素值存储到矩阵中
统计二值图中前景区域像素个数,记为n 创建一个3行n列的矩阵 rgbs1 同样rgbs1的三行对应 RGB三个分量中待匀色区域的像素 填充规则依然是第一列 从上到下 第二列从上到下,一直到最后一列 只不过这次只要前景区域的像素(就是说 当遍历到像素是背景像素时 不存到矩阵中)
好了 现在我们已经把它拿出来了 我们要把操作矩阵 rgbs1 了
这一步是 怎么训练
步骤③ 操作:
把待匀色区域形成的矩阵 rgbs1 和rgbt 按照上述(1)进行 缩放旋转平移
然后就得到结果矩阵I
怎么放回去
步骤④ 我们得到矩阵I以后 把I的三行对应RGB三个分量进行填充
比如 I的第一行 填到R分量中 第一行第一个元素填到R分量第一列的第一个非背景像素上,然后第一列填充完以后,继续从第二列的第一个非背景像素开始填充 一直到最后一列
I的第二行和第三行都是如此
so 很简单的就把 任意前景区域图像进行色彩处理了
主要思想就是拿出来 再放回去
看下颜色转移的效果:
把左边的匀成右边的

把亮的匀成暗的

相关文章:

任意区域的色彩一致性处理方法
影像任意感兴趣区域的色彩一致性处理方法,主要是针对掩膜后的影像,类似下图,对非背景区域的像素进行处理 其中非黑色部分我们叫待匀色区域。 这种处理 对于wallis 和直方图匹配 很容易实现,但是颜色转移就相对而言 困难点。 颜…...
听GPT 讲Istio源代码--pilot
File: istio/operator/pkg/translate/translate.go 在Istio项目中,istio/operator/pkg/translate/translate.go文件的作用是处理Istio Operator的配置信息和Kubernetes的资源对象之间的翻译和转换。 首先,scope和componentToAutoScaleEnabledPath是用于记…...
pdfjs解决ie浏览器预览pdf问题
pdfjs是一个js库,可以将pdf文件用canvas重新绘制,从而无需借助pdf读取插件就可以直接预览。 目前chrome内核的浏览器已内置pdf读取插件,但ie浏览器还没有。而我们最近在做的一个项目使用对象是医院,使用的浏览器竟然还是ie。所以我…...

千里共婵娟 | 结合微信公众号用JavaScript完整开发实现换中秋头像的功能
🏆作者简介,黑夜开发者,CSDN领军人物,全栈领域优质创作者✌,阿里云社区专家博主,2023年6月csdn上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师,项目技术负责…...

pt26django教程
admin 后台数据库管理 django 提供了比较完善的后台管理数据库的接口,可供开发过程中调用和测试使用 django 会搜集所有已注册的模型类,为这些模型类提拱数据管理界面,供开发者使用 创建后台管理帐号: [rootvm mysite2]# python3 manage.…...
javabasic
计算机基础 一、学前知识 1. 计算机组成 2. 进制的概念 (1)二进制的存储 计算机不管是内存还是硬盘,都是以二进制的形式存储。如同一张巨大的表格,里面都是由0和1组成。 二进制:逢2进1 基数为2,数值部分…...

电子词典项目
目录 目录 头文件:dict.h: 源文件:dict.c: 服务器测试文件:serDict.c: 客户端测试文件:cliDict.c: 头文件:dict.h: #ifndef __DICT_H__ #define __DICT_H__ #include<myhead.h> #include<sqlite3.h>#de…...
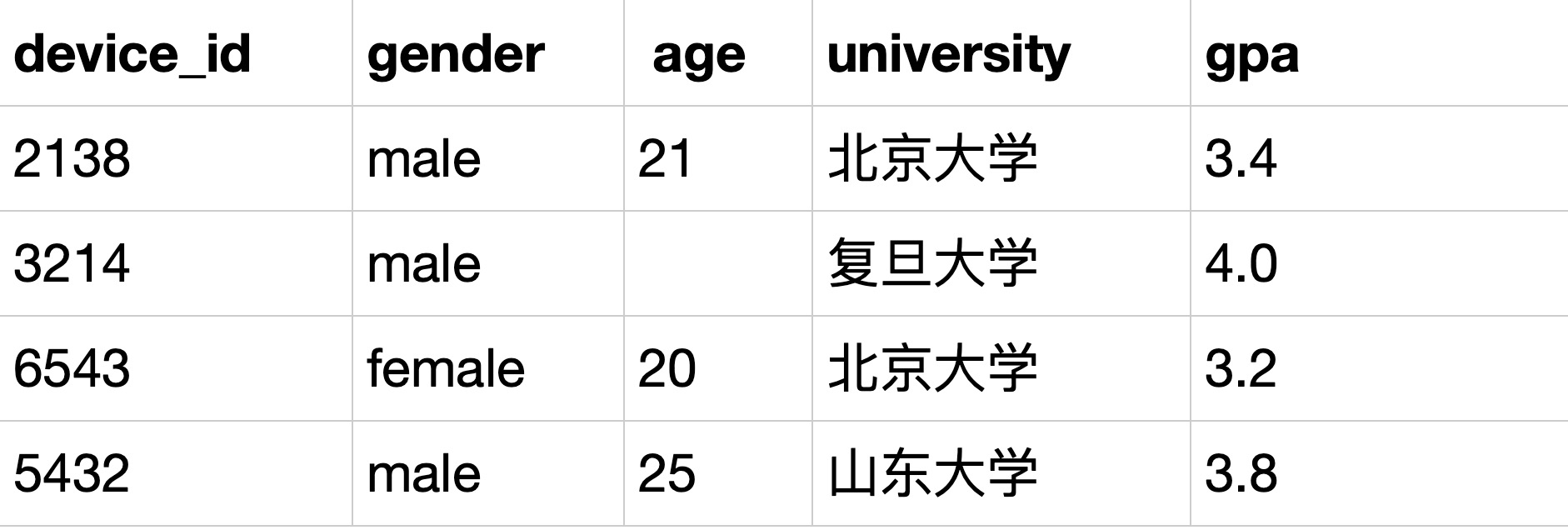
SQL12 高级操作符练习(2)
描述 题目:现在运营想要找到学校为北大或GPA在3.7以上(不包括3.7)的用户进行调研,请你取出相关数据(使用OR实现) 示例:user_profile iddevice_idgenderageuniversitygpa12138male21北京大学3.423214male复旦大学4.03…...

python写代码过程中的坑230915
1.解释代码IndentationError: expected an indented block 这个错误通常是由于代码缩进错误导致的。 在Python中,代码块(如循环、条件语句、函数等)通常使用缩进来表示。因此,如果你在期望缩进的位置没有正确缩进代码,就会出现"IndentationError: expected an inden…...
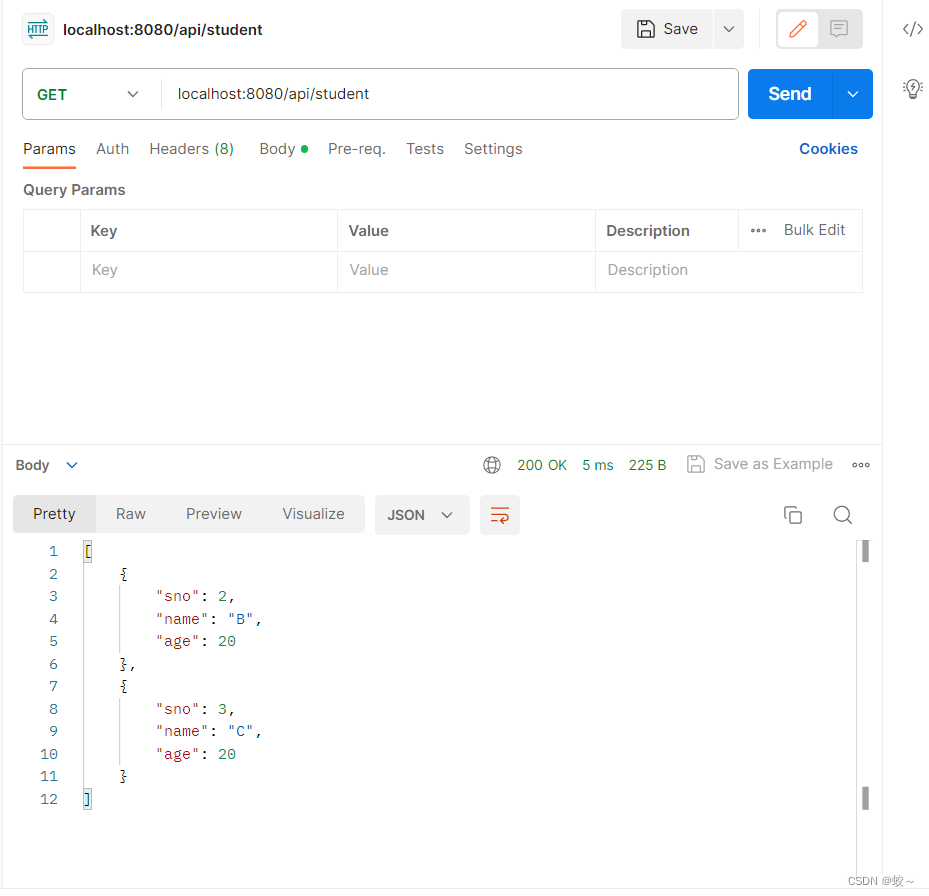
SpringBoot课堂笔记20230913
本篇文章为SpringBoot学习笔记,方便自己再复习。 Maven:jar包管理工具 注解: Controller:处理http请求,返回的视图 RestController: 相当于ResponseBody和Controller一起用,返回的是json ResponseBody:返回响应内容 …...

3D数字孪生:从3D数据采集到3D内容分析
数字孪生(Digital Twin)是物理对象、流程或系统的虚拟复制品,用于监控、分析和优化现实世界的对应物。 这些数字孪生在制造、工程和城市规划等领域变得越来越重要,因为它们使我们能够在现实世界中实施改变之前模拟和测试不同的场景…...

【杂记】git管理工具的相关应用
这里记录一些用git管理工具进行开发的命令,便于自己查看,我认为下面两篇博客写的很详细,但是为了自己方便查看,所以自己写了一些命令供自己进一步理解。gitee相对git来说更方便一些(毕竟国内的不用担心墙)&…...

看好多人都在劝退学计算机,可是张雪峰又 推荐过计算机,所以计算机到底是什么样 的?
张雪峰高考四百多分,但是他现在就瞧不起400多分的学生。说难听点,六七百分的 热门专业随便报谁不会啊? 计算机专业全世界都是过剩的,今年桂林电子科技,以前还是华为的校招大学,今年 计算机2/3待业。这个世…...

leetcode 26.删除有序数组中的重复项
给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums 的唯一元素的数量为 k ,你需要做…...

jitsi音视频会议集成到自己的网页中
将jitsi视频会议集成到自己的web网站: 源码: <!DOCTYPE html> <html lang"en" xmlns:th"http://www.thymeleaf.org"> <head><meta charset"UTF-8"><meta name"viewport" content&…...
浅析Java责任链模式实现
一、概要 定义:责任链模式是一种行为设计模式, 允许你将请求沿着处理者链进行发送。收到请求后, 每个处理者均可对请求进行处理, 或将其传递给链上的下个处理者。 二、应用场景: 1.多条件流程判断:权限相关…...

SpringBoot雪花算法主键ID传到前端后精度丢失问题的解决
Java后端Long类型的范围 -263~263,即:-9223372036854775808~9223372036854775807,它是19位的。 这个数字可以通过方法获得:Long.MAX_VALUE、Long_MIN_VALUE。 前端JS的数字类型的范围 -253~253,即:-9007…...

vue使用elementUI的upload上传文件封装
这篇文章的目的 将文件上传的方法封装一下,供大家统一调用, 话不多说,直接上代码 upload 核心参数说明 action 上传的地址accept 接受上传的文件类型multiple 是否开启多文件上传模式limit 限制上传个数fileList 文件列表disabled 是否禁用 upload 核心方…...

cenos自动启动tomcat
首先创建一个脚本 关闭tomcat 等待2分钟 启动tomcat 并且把日志输出在 /usr/local/tomcat/tomcatchognqi.log #!/bin/bashexport JAVA_HOME/usr/local/jdk/jdk1.8.0_211 export JRE_HOME$JAVA_HOME/jre# 日志文件路径和文件名 LOG_FILE"/usr/local/tomcat/tomcatchognqi.…...
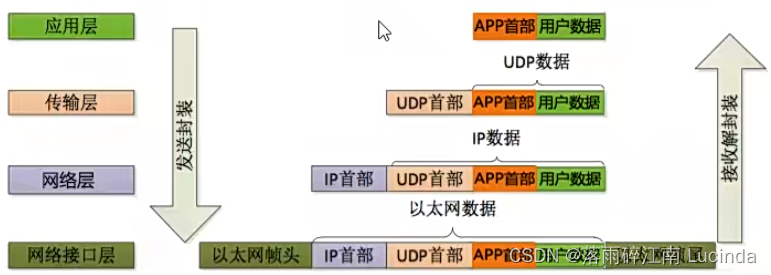
OSI模型与数据的封装
1、OSI模型 上层|| 七层模型 四层模型|| 应用层| 表示层 应用层 http/ftp/ssh/ftps| 会话层 -----------------------------------------------------------------------| 传输层 传输层 tcp/udp ------------------------------…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...
