(手撕)数据结构--->堆
文章内容
目录
一:堆的相关概念与结构
二:堆的代码实现与重要接口代码讲解
让我们一起来学习:一种特殊的数据结构吧!!!!
一:堆的相关概念与结构
在前面我们已经简单的学习过了二叉树的链式存储结构了,那么二叉树的顺序存储结构是啥呢?其实二叉树的顺序存储结构我们一般将他叫做堆。
二叉树为啥有两种形式的存储结构呢?因为堆是一种特殊的二叉树,它特殊的地方在于它的逻辑结构实际上是一颗完全二叉树,在物理结构上我们一般用数组来表示堆的结构,而如果不是完全二叉树我们一般不会用数组成为二叉树的结构,因为假如不是完全二叉树那么我们数组可能会浪费大量的空间。
用数组作为二叉树的结构的时候我们必须要知道的双亲结点与子节点的下标关系为:
leftchild=parent*2+1;
rightchild=parent*2+2;
parent=(child-1)/2;(child可以是左孩子也可以是右孩子)
如图:完全二叉树与非完全二叉树在使用顺序存储结构的区别:
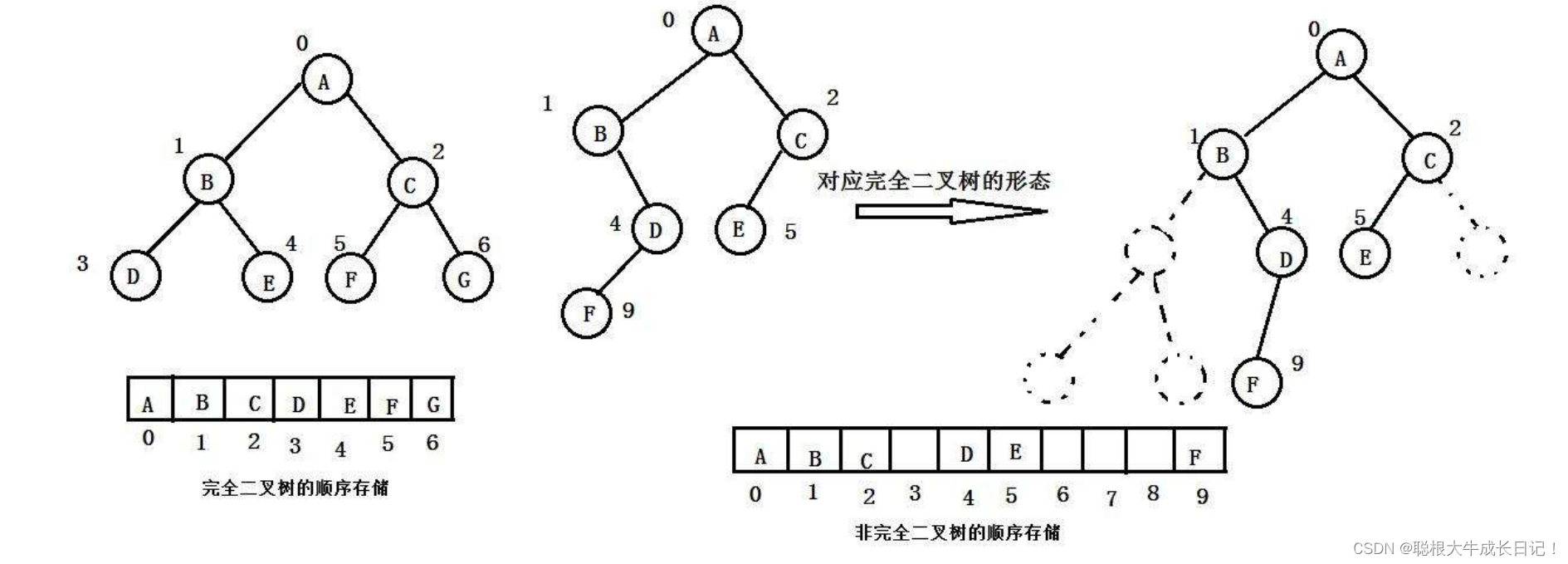
在这里就能看出当结构不同时,我们需要采取不同的形式进行表示。
总结:堆在逻辑结构上是一棵完全二叉树,在物理结构上是一个数组。对于非完全二叉树我们不适用数组的结构表示二叉树。
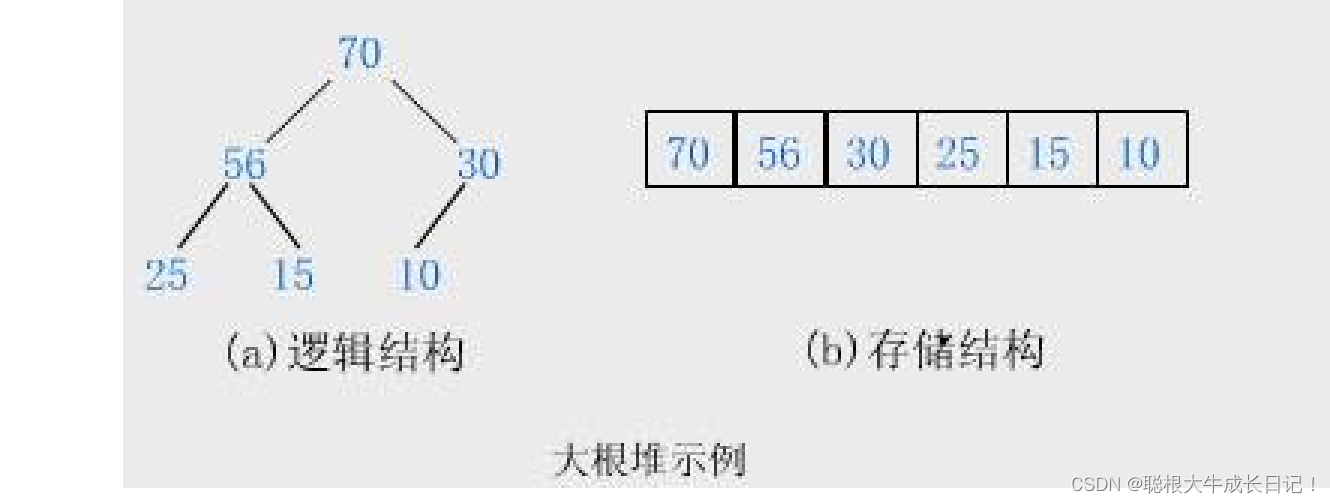
堆的两种形式(判断数组是不是堆的方式)
大堆:树中所有的父亲结点都大于或等于孩子结点,且根节点的值是堆中最大的数据。
小堆:树中所有的父亲结点都小于或等于孩子结点,且根节点的值是堆中最小的数据。
这也引出了堆的特点:1:堆中某个结点的值总是不大于或不小于父亲结点的值。
2:堆总是一棵完全二叉树。

二:堆的代码实现与接口的讲解
由于堆所具有的特点我们定义堆的结构为一个数组,与我们的顺序表,栈的结构类似。
代码:
typedef int HeapDataType;typedef struct Heap
{HeapDataType* a;int Size;int Capacity;
}HP;
接下来就是我们熟悉的接口了,一些不难理解的接口我就直接跳过,对其它类型的接口进行讲解。
初始化堆:其实这个接口有两种初始化的代码:1:就是不开辟空间,等我们实际插入数据的时候来考虑增容和开辟空间。2:是传入一个数组然后将这个数组里面的值拷贝到我们需要开辟的空间当中。
代码如下:
void InitHeap(HP* php)
{assert(php);php->a = NULL;php->Size = php->Capacity = 0;
}
堆的销毁:直接销毁我们动态开辟的空间。
代码如下:
void DestoryHeap(HP* php)
{assert(php);free(php->a);php->a = NULL;php->Capacity = php->Size = 0;
}接下来我们先讲两个重要的关于堆的算法向上调整算法与向下调整算法
首先这两个算法的时间复杂度都是log(N)
这两个算法在建堆的时候作用很大
我们先讲解
向上调整算法
前提:我们所插入的值前面的结构必须是堆
接下来我们通过图的方式来讲解这个算法的工作原理

代码实现:
void AdjustUp(HeapDataType* a, int child)
{int parent = (child - 1) / 2;//交换的过程while (child>0){if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}总结算法思想:以建大堆为列,将插入的值与双亲进行比较,如果插入的值大于它的双亲的值,那么就交换孩子与双亲,可能我们插入的值非常大,那么可能会到达根节点所以我们使用循环来进行完成,最坏的情况就是我们要向上调整高度次,而完全二叉树的高度我们之前也算过,所以时间复杂度为:log(N);
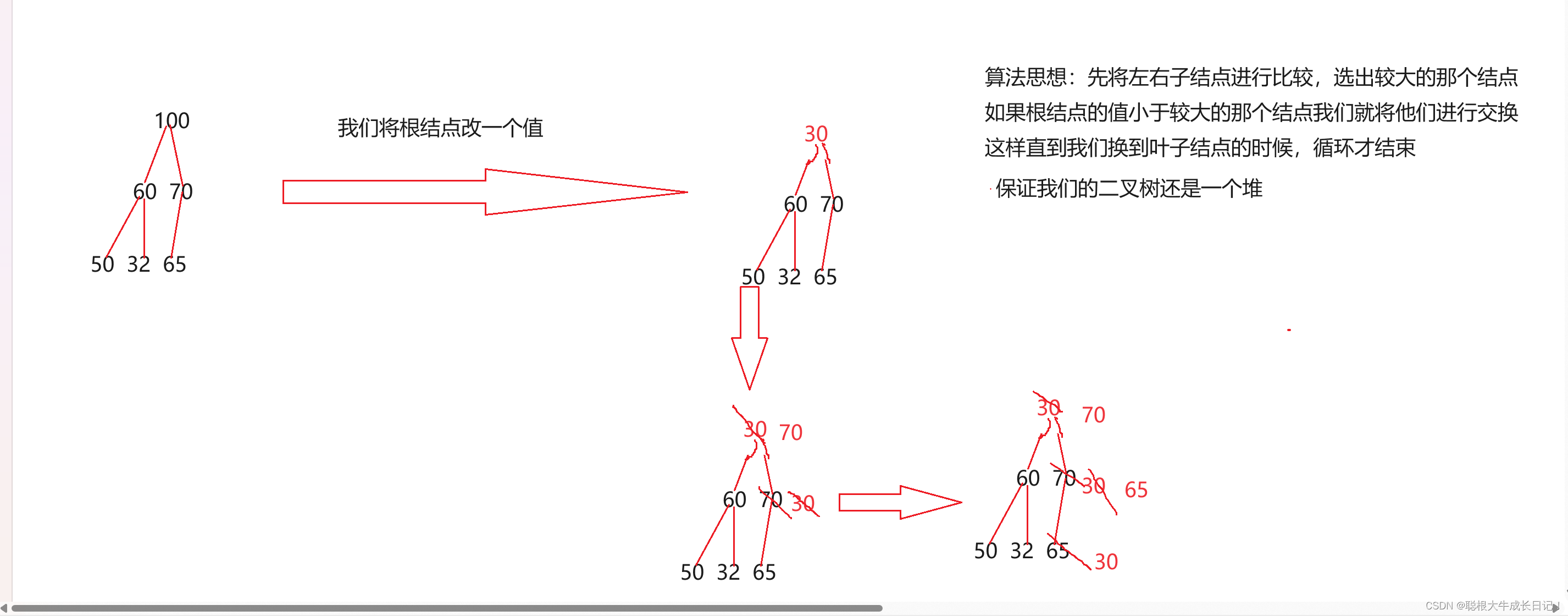
向下调整算法
使用前提:左右子树都是堆
简单图解向下调整算法:
代码如下:
void AdjustDown(HeapDataType* a, int n, int parent)
{int child = parent * 2 + 1;while (child < n){//找小的那个孩子if (child+1<n && a[child] >a[child + 1] ){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}代码是按小堆而写的
注意:这里我们需要考虑到一种特殊的情况,就是当我们孩子结点为最后一个结点的时候那么我们对下标为child+1的结点访问时会越界,而且我们在判断左右孩子谁小的时候我们不需要假定左孩子小这样会有几种情况且很麻烦,所以我们先假定要左孩子小,每次在判断孩子与双亲结点谁小的前面,先拿左孩子右有孩子相互比较,然后我们取小的就行。
总结算法思想:将父亲结点与孩子结点中小的结点进行比较,然后按照时大堆还是小堆的逻辑进行相互的比较,当孩子结点为叶子结点的时候循环终止。
插入接口:要保证插入之后我们的堆还是原来的大小堆。
思想:我们先尾插一个值,然后将这个值进行向上调整,且每次在插入之前我们都需要进行扩容逻辑的判断。
代码如下:
void PushHeap(HP* php, HeapDataType x)
{assert(php);//先尾插到数组中去//先判断空间是否足够if (php->Capacity == php->Size){int newcapacity = php->Capacity == 0 ? 4 : php->Capacity * 2;HeapDataType* tmp = (HeapDataType*)realloc(php->a, sizeof(HeapDataType) * newcapacity);if (tmp == NULL){perror("realloc fail:");exit(-1);}php->a = tmp;php->Capacity = newcapacity;}php->a[php->Size] = x;AdjustUp(php->a, php->Size);php->Size++;
}总结:扩容,插入,向上调整,这几个步骤就能将这个接口给实现。
堆的删除接口:这个接口需要借助向下调整算法来解决
接口作用,能够将二叉树中最大或最小的结点值给删除,让第二大或第二小结点的值展示出来。
算法思想:我们并不是通过移动空间来将二叉树中根节点的值给删除,因为顺序表的尾插的时间效率非常的大,所以我们一般时首先将根节点的值与最后一个值进行交换,然后再将交换后的结点进行向下调整,这样做可以得到第二大或小的值。
代码:
void PopHeap(HP* php)
{assert(php);//得有元素才能删除assert(php->Size > 0);//删除的步骤//1先将根结点与尾结点交换,在删除最后一个结点Swap(&php->a[0], &php->a[(php->Size) - 1]);--(php->Size);//2在进行向下调整AdjustDown(php->a, php->a[0],0);
}总结:在删除之前我们还需要看我们的堆是否含有结点,然后在交换,向下调整,就可以完成这个接口了。
这个接口与判空接口和取堆顶接口,能让我们对我们的数据打印出来是升序的或者是降序的。
取堆顶元素的接口
思想:直接返回数组中元素下标为0的值就行
代码:
HeapDataType HeapTop(HP* php)
{assert(php);assert(php->Size > 0);return php->a[0];
}判断堆有多少个元素的接口
直接return size就行
int HeapSize(HP* php)
{assert(php);return php->Size;
}堆的判空:只需要看size为不为0就行
bool HeapEmpty(HP* php)
{assert(php);return php->Size == 0;
}本章结束!!!欢迎大家的耐心观看

相关文章:

(手撕)数据结构--->堆
文章内容 目录 一:堆的相关概念与结构 二:堆的代码实现与重要接口代码讲解 让我们一起来学习:一种特殊的数据结构吧!!!! 一:堆的相关概念与结构 在前面我们已经简单的学习过了二叉树的链式存储结…...

[运维|数据库] MySQL 中的COLLATE在 PostgreSQL如何表示
在 PostgreSQL 中,字符集(collation)和排序规则(collation order)的概念与 MySQL 类似,但语法和用法略有不同。在 PostgreSQL 中,字符集和排序规则通常是数据库、表或列级别的设置,而…...

【Linux】tar 与 zip 命令
tar 命令 tar 本质上只是一个打包命令,可以将多个文件或者文件夹打包到一个 tar 文件中,结合其他的压缩程序再将打包后的档案文件压缩。 所以看到 .tar.gz, .tar.bz2, .tar.xz 等等文件其实是 tar 文件之后进行 Gzip, Bzip2, XZ 压缩之后的文件。 tar…...

VS2015+opencv 3.4.6开发环境
VS2015+opencv 3.4.6开发环境 一、安装包下载二、安装过程三、VS环境配置四、测试一、安装包下载 这里提供两种下载方法: 1. opencv官网 2. csdn资源下载 二、安装过程 2.1 下载opencv-3.4.6 安装包 2.2 双击开始安装,选择要安装目录,点击Extract。 2.3 等待解…...
) * 1000转为PostgreSQL的语法)
[运维|数据库] 将mysql的null.unix_timestamp(now()) * 1000转为PostgreSQL的语法
在 PostgreSQL 中,您可以使用以下方式将 MySQL 中的 UNIX_TIMESTAMP 和 NOW() 函数的组合转换为等效的语法: EXTRACT(EPOCH FROM NOW()) * 1000在这个 PostgreSQL 表达式中: EXTRACT(EPOCH FROM NOW()) 获取当前时间戳的秒数。 2. * 1000 将…...

springboot使用filter增加全局traceId,方便日志查找
一:引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-web</artifactId></dependency> 二:编写过滤器: package com.example.demo.filter;import or…...

面经学习三
目录 Java 与 C 的区别 面向对象和面向过程的区别 面向对象特性 Java的基本数据类型 深拷贝和浅拷贝 Java创建对象的几种方式 final, finally, finalize 的区别 Java 与 C 的区别 Java 是纯粹的面向对象语言,所有的对象都继承自 java.lang.Object,…...

Open3D 点云配准——可视化匹配点对之间的连线
点云配准 一、算法原理1、概述2、主要函数二、代码实现三、结果展示四、测试数据本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 一、算法原理 1、概述 可视化源点云和目标点云中匹配点对之间的连线,这对于点云配准,尤…...

io多路复用之poll的详细执行过程
1.结构体struct pollfd的定义 struct pollfd { int fd; /* 文件描述符 */ short events; /* 想要监视的事件(input/output/priority) */ short revents; /* 实际发生的事件(返回的事件) */ }; 2.定义po…...
网络安全深入学习第四课——热门框架漏洞(RCE— Log4j2远程代码执行)
文章目录 一、log4j2二、背景三、影响版本四、漏洞原理五、LDAP和JNDI是什么六、漏洞手工复现1、利用DNSlog来测试漏洞是否存在2、加载恶意文件Exploit.java,将其编译成class文件3、开启web服务4、在恶意文件Exploit.class所在的目录开启LDAP服务5、监听反弹shell的…...

大数据Flink(八十一):SQL 时区问题
文章目录 SQL 时区问题 一、SQL 时区解决的问题...
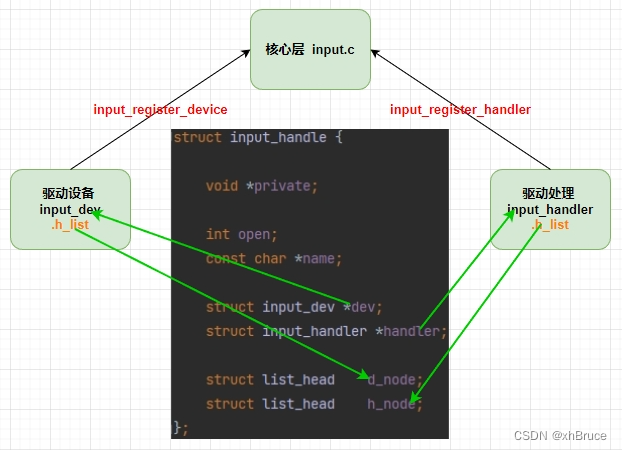
Input子系统 - Kernel驱动程序 - Android
Input子系统 - Kernel驱动程序 - Android 1、Input子系统相关定义1.1 代码位置1.2 input_dev结构体:表示输入设备1.3 input_handler结构体:struct input_handler - implements one of interfaces for input devices1.4 input_handle结构体:将…...
MySQL里的查看操作
文章目录 查看当前mysql有谁连接查看数据库或者表 查看当前mysql有谁连接 show processlist;查看数据库或者表 列出所有数据库: show databases;查看正在使用的数据库(必须大写): SELECT DATABASE();列出数据库中的表…...
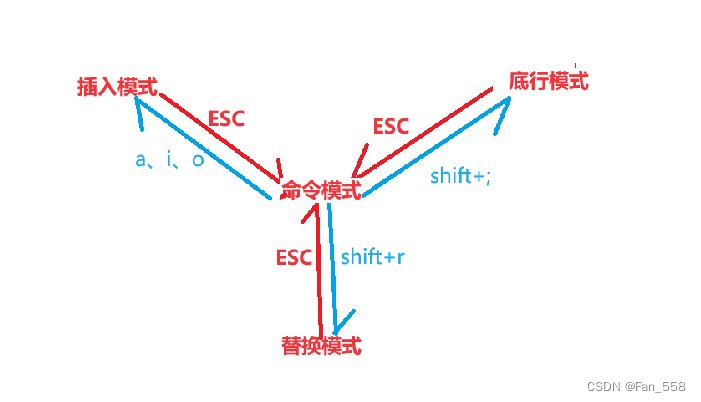
Vim的基础操作
前言 本文将向您介绍关于vim的基础操作 基础操作 在讲配置之前,我们可以新建一个文件 .vimrc,并用vim打开在里面输入set nu 先给界面加上行数,然后shift ;输入wq退出 默认打开:命令模式 在命令模式中:…...

十天学完基础数据结构-第一天(绪论)
1. 数据结构的研究内容 数据结构的研究主要包括以下核心内容和目标: 存储和组织数据:数据结构研究如何高效地存储和组织数据,以便于访问和操作。这包括了在内存或磁盘上的数据存储方式,如何将数据元素组织成有序或无序的集合&…...
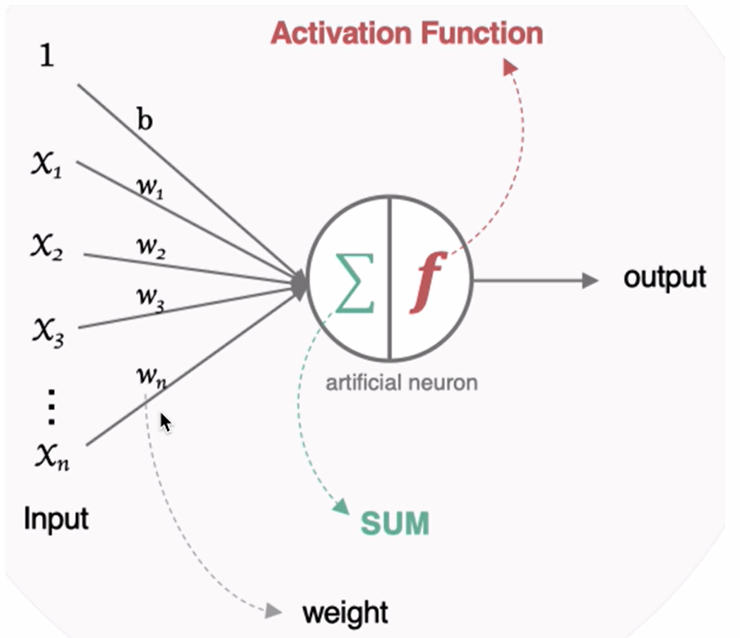
神经网络 03(参数初始化)
一、参数初始化 对于某一个神经元来说,需要初始化的参数有两类:一类是权重W,还有一类是偏置b,偏置b初始化为0即可。而权重W的初始化比较重要,我们着重来介绍常见的初始化方式。 (1)随机初始化 …...

div设置圆角#前端
要在 div元素上设置圆角,您可以使用 CSS 的 border-radius 属性。 这个属性允许您指定元素的边角为圆角,可以将其应用于一个或多个边角。以下是一些示例代码:1.设置所有四个边角为圆角: div {border-radius: 10px; /* 设置所有四…...
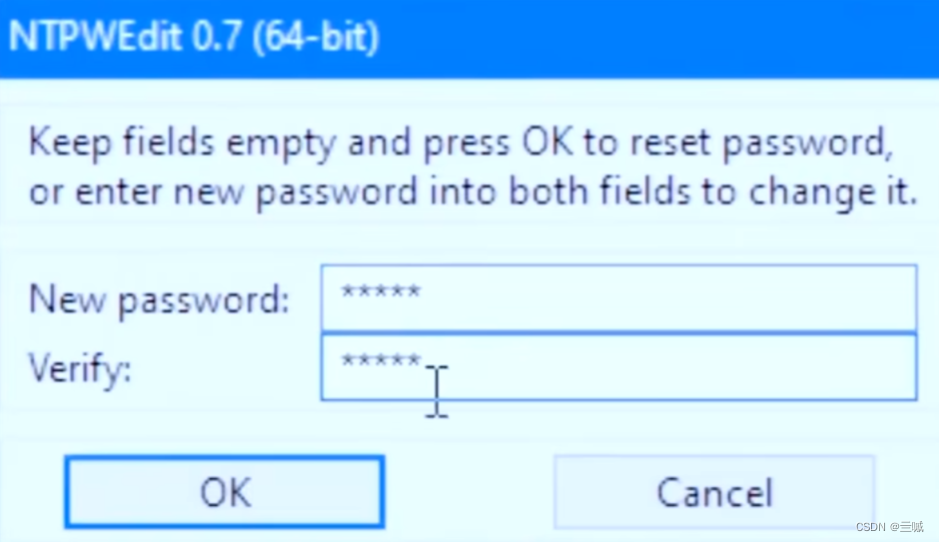
Windows开机密码破解
Windows11以及Windows10(21H2)以上版本 先开机,不进行任何操作,静静的等待登录界面 按住Shift重启 进入“选择一个选项”界面,点击疑难解答 点击高级选项 点击命令提示符 输入两行命令 copy C:\windows\system32\uti1man.exe C: \Window…...
Mobirise for Mac:轻松创建手机网站的手机网站建设软件
如果你是一位设计师或者开发人员,正在寻找一款强大的手机网站建设软件,那么Mobirise for Mac绝对值得你尝试。这个独特的应用程序将帮助你轻松创建优雅而实用的手机网站,而无需编写复杂的代码。 Mobirise for Mac的主要特点包括:…...

[npm] npx 介绍与使用说明
[npm] npx 介绍与使用说明 npm 的由来npx 是什么?npx 特点npx 的特点项目安装包的使用全局安装包的避免指定工具包版本--no-install 参数和--ignore-existing 参数使用不同版本的 node-p 参数-c 参数实战应用 执行 GitHub 源码 npm 的由来 说到 npm 就离不开社区文…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
