uni-app监听页面滚动
在uni-app中可以通过监听页面滚动事件来实现滚动效果或响应滚动事件
- 在需要监听滚动的页面或组件中,添加一个
scroll元素,用于容纳内容并实现滚动效果。<template><view class="container"><scroll-view scroll-y @scroll="onPageScroll" class="scroll-content"><!-- 页面内容 --></scroll-view></view> </template><style> .container {height: 100vh; }.scroll-content {height: 100%; } </style> - 在页面或组件的方法中添加对应的滚动事件处理函数。
export default {methods: {onPageScroll(event) {// 滚动事件处理逻辑console.log(event.scrollTop)// 根据scrollTop的值来执行相应操作}} }
相关文章:

uni-app监听页面滚动
在uni-app中可以通过监听页面滚动事件来实现滚动效果或响应滚动事件 在需要监听滚动的页面或组件中,添加一个scroll元素,用于容纳内容并实现滚动效果。 <template><view class"container"><scroll-view scroll-y scroll"…...
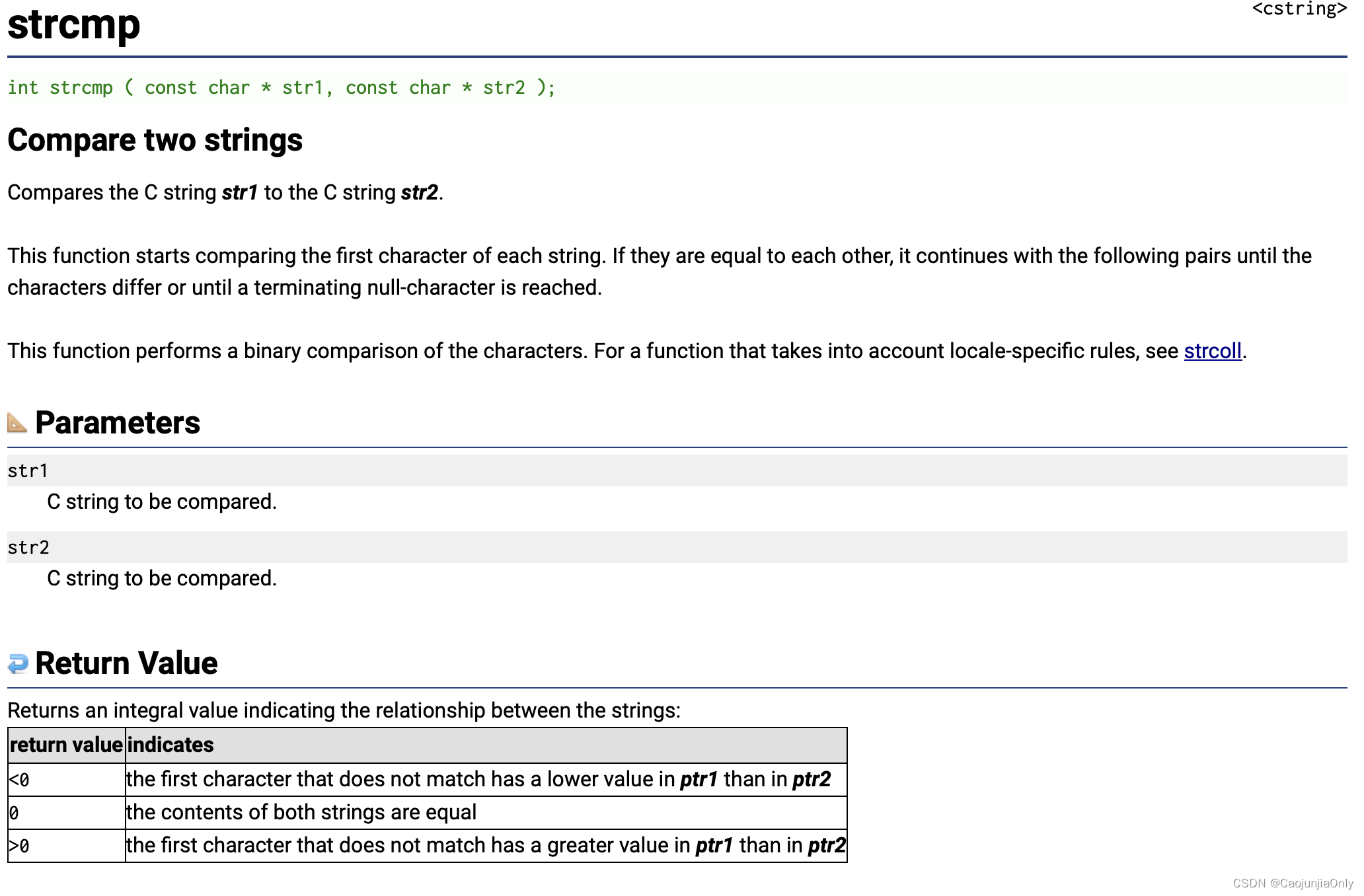
[字符串和内存函数]strcmp字符串函数的详解和模拟
strcmp函数 strcmp函数是一个用于比较两个字符串的C标准库函数。它的原型为: int strcmp(const char* str1, const char* str2);strcmp函数会比较str1和str2两个字符串的字符序列,并返回一个整数值来表示它们之间的大小关系。返回值的含义如下ÿ…...

zookeeper 常见问题处理
调整jvm参数 [rootvm-02 conf]# cat /opt/app/zookeeper-3.4.14/bin/zkEnv.sh |grep java.env -A3 -B3ZOOCFG"$ZOOCFGDIR/$ZOOCFG"if [ -f "$ZOOCFGDIR/java.env" ] then. "$ZOOCFGDIR/java.env" fiif [ "x${ZOO_LOG_DIR}" "x&…...

repo 命令
repo命令是Google开发的用于管理Android版本库的一个工具。 repo命令并不是用于取代git,而是用Python对git进行了一定的封装,简化了对多个Git版本库的管理。 repo init -u -b -m <manifest 文件名称> repo sync 相当于 git clone 获取 git remote…...

一、 计算机网络概论
一、计算机网络概论 1、计算机网络概述 1.1、概念 计算机网络是一个将分散的、具有独立功能的计算机系统,通过通信设备与线路连接起来,由功能完善的软件实现资源共享和信息传递的系统 是一些互连的、自治的计算机系统的集合 以能够相互共享资源的方…...

从零学习开发一个RISC-V操作系统(一)丨计算机组成原理相关知识与RISC-V指令集简介
本篇文章的内容 一、计算机组成原理的相关知识1.1 计算机的硬件组成1.2 程序的存储与执行1.3 程序语言的设计和进化1.4 存储设备的层次结构1.5 操作系统 二、RISC-V的指令集ISA简介2.1 什么是ISA2.2 复杂指令集(CISC)和精简指令集(RISC&#…...
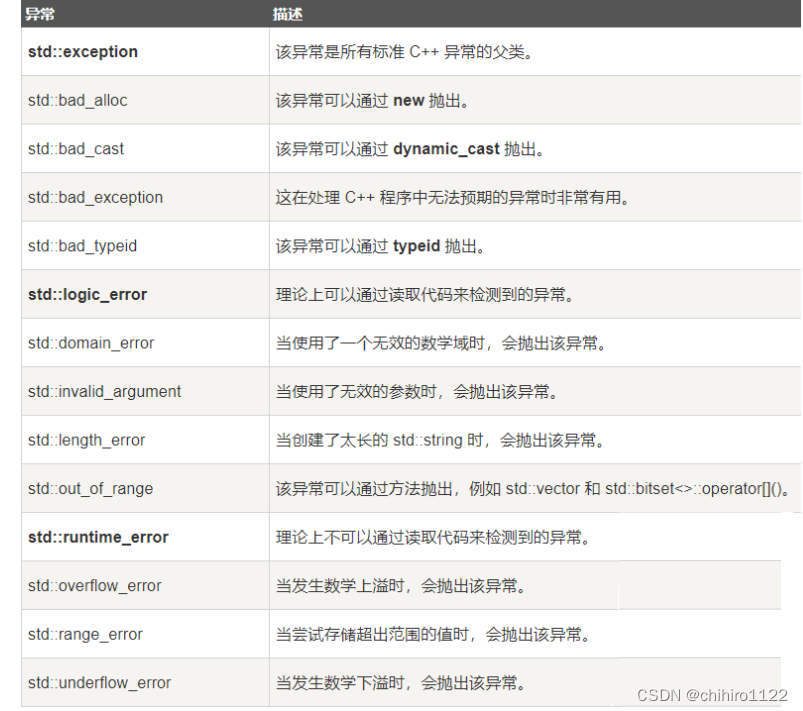
C++ - 异常介绍和使用
前言 我们在日常编写代码的时候,难免会出现编写错误带来程序的奔溃,或者是用户在使用我们编写的程序时候,使用错误所带来程序的奔溃。 在C 当中 可以对你觉得可能发生 错误 的地方在运行之前进行判断,发生错误可以给出提示。 C…...
iText实战--在现有PDF上工作
6.1 使用PdfReader读取PDF 检索文档和页面信息 D:/data/iText/inAction/chapter03/image_direct.pdf Number of pages: 1 Size of page 1: [0.0,0.0,283.0,416.0] Rotation of page 1: 0 Page size with rotation of page 1: Rectangle: 283.0x416.0 (rot: 0 degrees) Is reb…...
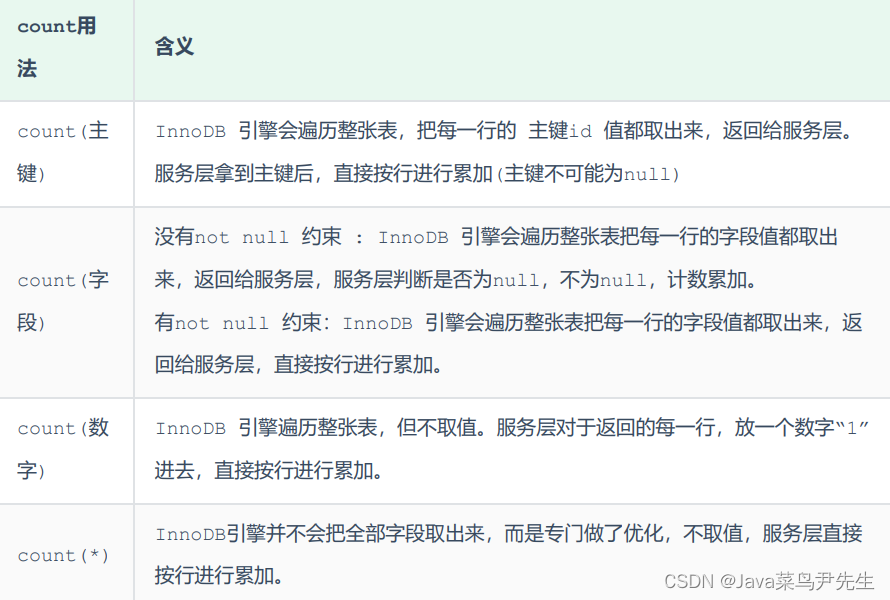
SQL优化--count优化
select count(*) from tb_user ;在之前的测试中,我们发现,如果数据量很大,在执行count操作时,是非常耗时的。 MyISAM 引擎把一个表的总行数存在了磁盘上,因此执行 count(*) 的时候会直接返回这个 数,效率很…...
IDEA下使用Spring MVC
<?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0.0 http://ma…...
)
2022基金从业人员资格管理及后续职业培训 部分答案(自答)
2022基金从业人员资格管理及后续职业培训 区块链在金融交易后处理中的应用私募基金行业典型违法案例分析《证券法》修订情况报告《刑法修正案(十一)》金融犯罪条款中国结算港股通结算业务介绍商品投资与商品配置价值气候技术:实现双碳目标的技…...

阿里云通义千问向全社会开放,近期将开源更大参数规模大模型
9月13日,阿里云宣布通义千问大模型已首批通过备案,并正式向公众开放,广大用户可登录通义千问官网体验,企业用户可以通过阿里云调用通义千问API。 通义千问在技术创新和行业应用上均位居大模型行业前列。IDC最新的AI大模型评估报告…...

数据结构:二叉查找树
文章目录 二叉查找树一,概述二,添加数据三,删除数据 二叉查找树 一,概述 二叉查找树,也称为二叉搜索树,是一种特殊的二叉树,它或者是一颗空树,或者具有以下性质:对于每…...

Redis的介绍,安装Redis的方式
🐌个人主页: 🐌 叶落闲庭 💨我的专栏:💨 c语言 数据结构 javaEE 操作系统 石可破也,而不可夺坚;丹可磨也,而不可夺赤。 Redis 初识Redis1.1 认识Redis1.2 安装Redis的方式…...

深入理解CI/CD流程:改变你的开发生命周期
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
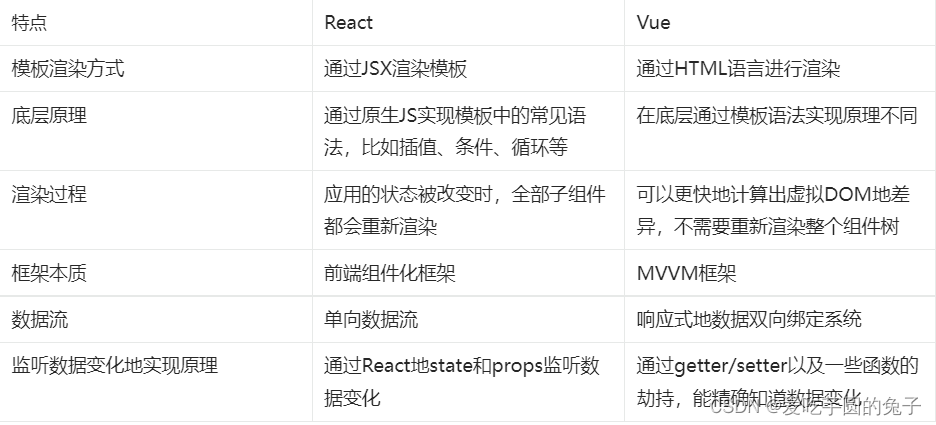
【React】React入门
目录 一、何为React二、React与传统MVC的关系三、React的特性1、声明式编程①、实现标记地图 2、高效灵活3、组件式开发(Component)①、函数式组件②、类组件(有状态组件)③、一个组件该有的特点 4、单向式响应的数据流 四、虚拟DOM1、传统DOM更新①、举…...
面相面试知识--Lottery项目
面相面试知识–Lottery项目 1.设计模式 为什么需要设计模式? (设计模式是什么?优点有哪些?) 设计模式是一套经过验证的有效的软件开发指导思想/解决方案;提高代码的可重用性和可维护性;提高团…...

《Python趣味工具》——自制emoji2(2)
今天,我们将会完成以下2个内容: 绘制静态emoji总结turtle中常用的绘图函数 文章目录 一、绘制静态emoji::sparkles: 画脸::sparkles:绘制嘴巴::sparkles:绘制眼白:绘制眼白-Part1:绘制眼白—pa…...

【面试刷题】——C++四种类型转化
C支持多种类型转换操作,其中包括四种主要类型转换方式: 隐式类型转换(Implicit Conversion): 隐式类型转换是自动发生的类型转换,由编译器自动完成。 它用于处理不同数据类型之间的运算,例如将…...
集成Activiti-Modeler流程设计器
集成Activiti-Modeler流程设计器 Activiti Modeler 是 Activiti 官方提供的一款在线流程设计的前端插件,可以方便流程设计与开发人员绘制流程图,保存流程模型,部署至流程定义等等。 1、材料准备 首先我们需要获取activiti-explorer.zip&…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
