C#回调函数学习1
回调函数(Callback Function)是一种函数指针,它指向的是由用户自己定义的回调函数。我们将这个回调函数的指针作为参数传递给另外一个函数,在这个函数工作完成后,它将通过这个回调函数的指针来回调通知调用者处理结果。
此定义来自网上;
看一个例子;这是用委托实现的回调函数;
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;namespace myhd1
{public partial class Form1 : Form{private delegate void MyDelegate(int a); //定义一个委托类型public Form1(){InitializeComponent();}private void button1_Click(object sender, EventArgs e){myFuncWithCallback(15, new MyDelegate(MyCallBack));}private void myFuncWithCallback(int b, MyDelegate callback){int result = b * b;callback(result);}private void MyCallBack(int n){textBox1.Text = n.ToString();}}
}private delegate void MyDelegate(int a);
定义一个委托,无返回值,有一个整型参数;
myFuncWithCallback是一个用户定义函数,一个带有回调函数的函数;
MyCallBack(int n)
{
.......
}
这是回调函数体;
new MyDelegate(MyCallBack),这是实例化委托;
单击按钮时调用了myFuncWithCallback,然后也会执行回调函数;
运行如下;
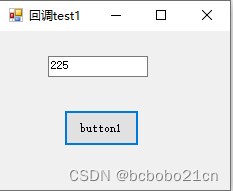
假设不用回调函数;代码是如下,
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
private void button1_Click(object sender, EventArgs e)
{
myFuncWithCallback(15);
}
private void myFuncWithCallback(int b)
{
int result = b * b;
MyCallBack(result);
}
private void MyCallBack(int n)
{
textBox1.Text = n.ToString();
}
}
功能也是一样;
但是使用回调函数实现了异步;myFuncWithCallback和MyCallBack之间是异步的;
异步是什么?
异步
不用等所有操作等做完,就可以做其他的处理(比如发消息,发完后,我不需要等你回复,就可以做其他处理)
同步
必须等所有的操作都做完,才返回给用户结果;
再看一个例子;枚举窗口,
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
using System.Runtime.InteropServices;namespace myhd2
{public partial class Form1 : Form{public delegate void CallBack(int hwnd, int lParam);[DllImport("user32")]public static extern int EnumWindows(CallBack x, int y);public Form1(){InitializeComponent();}private void button1_Click(object sender, EventArgs e){CallBack myCallBack = new CallBack(Report);EnumWindows(myCallBack, 0); }private void Report(int hwnd, int lParam){textBox1.Text += "Window handle is " + hwnd.ToString() + ";" + Environment.NewLine;} }
}Win32 api的EnumWindows函数枚举所有屏幕上的顶层窗口,并将窗口句柄传送给应用程序定义的回调函数;运行如下;
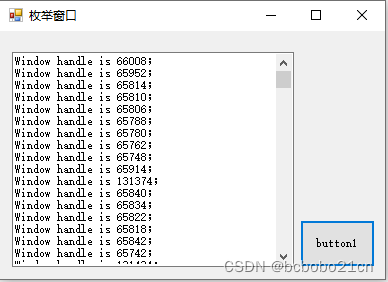
枚举和打印输出是异步的;
相关文章:

C#回调函数学习1
回调函数(Callback Function)是一种函数指针,它指向的是由用户自己定义的回调函数。我们将这个回调函数的指针作为参数传递给另外一个函数,在这个函数工作完成后,它将通过这个回调函数的指针来回调通知调用者处理结果。…...

leetcode 232 用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类: void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移除并返回元素int peek() 返回队列开头…...

element UI表单验证,自定义验证规则
validator 可以为指定字段自定义验证函数——这就相当于把前边配置的东西用js按照以前的方式编写验证逻辑了。虽然麻烦点,但是能实现比较复杂的业务逻辑判断。 <el-form-itemlabel"中奖概率"prop"rate":rules"[{ required: true, mes…...

redis 主存复制
1. 前言 Redis的持久化机制,它很好的解决了单台Redis服务器由于意外情况导致Redis服务器进程退出或者Redis服务器宕机而造成的数据丢失问题。 在一定程度上保证了数据的安全性,即便是服务器宕机的情况下,也可以保证数据的丢失非常少。 通常…...

Unity Shader顶点数据疑问
1)Unity Shader顶点数据疑问 2)Unity 2018发布在iOS 16.3偶尔出现画面不动的问题 3)安卓游戏启动后提示“应用程序异常” 这是第352篇UWA技术知识分享的推送,精选了UWA社区的热门话题,涵盖了UWA问答、社区帖子等技术知…...
java写一个用于生成雪花id的工具类
我们创建一个类 叫 SnowflakeIdGenerator 作为生成雪花id的工具类 然后 编写代码如下 public class SnowflakeIdGenerator {private static final long START_TIMESTAMP 1609459200000L; // 设置起始时间戳,可以根据需要进行调整private static final long WORKER…...
淘宝开店装修教程 (2023新版)
一、下载千牛 1. 浏览器打开淘宝 https://www.taobao.com/ 2. 进入 - 千牛卖家中心 3. 进入 - 关于千牛 4. 下载千牛 5. 下载页面 6. 下载安装桌面 二、登录千牛 1. 登录页面 2. 进入 - 千牛工作台 三、pc店铺装修 1. 进入 - pc店铺 2. 进入 - 装修页面 3. 删除没用的模块 从…...
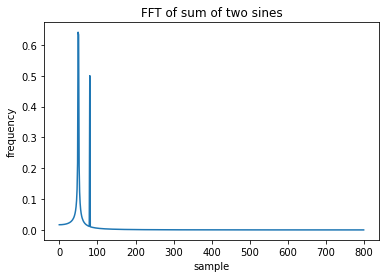
Python傅立叶变换
1. 什么是傅里叶变换? 在数学中,变换技术用于将函数映射到与其原始函数空间不同的函数空间。傅里叶变换时也是一种变换技术,它可以将函数从时域空间转换到频域空间。例如以音频波为例,傅里叶变换可以根据其音符的音量和频率来表示…...

MATLAB向量化编程基础精讲教程
向量化编程是MATLAB中一种重要的编程技术,通过使用向量和矩阵运算代替循环,可以提高代码的执行效率和可读性。本文将介绍MATLAB向量化编程的基础知识,并提供多个案例代码,帮助读者理解和应用向量化编程。 一、向量化编程基础知识…...

【非对称加密算法】RSA算法
一、非对称加密算法 非对称加密算法使用了两个不同的密钥:公钥和私钥。公钥是公开的,可以被任何人使用,而私钥是只有特定的人能够使用的。这种算法的加密和解密过程使用不同的密钥,因此称为非对称加密算法。 在非对称加密算法中…...

【滑动窗口】438. 找到字符串中所有字母异位词
438. 找到字符串中所有字母异位词 滑动窗口解法 创建两个Map 一个记录实际需要的有效字符 另一个记录窗口内的有效字符个数初始化need每次遍历一个字符 判断是不是有效字符 如果是 更新window 另外判断window中有效字符的个数是不是等于need中有效字符的个数 如果是更新valid…...

【PowerQuery】Excel 一分钟以内刷新PowerQuery数据
当需要进行刷新的周期如果小于一分钟,采用数据自动刷新就无法实现自动刷新的目标。那就没有办法了吗?当然不是,这里就是使用VBA来实现自动刷新。这里实现VBA刷新的第一步就是将当前的Excel 保存为带有宏的Excel 文件,如果不带宏则无法运行带有宏代码的Excel文件,保存过程如…...
【C语言】用冒泡排序实现my_qsort
大家好,我是苏貝,本篇博客带大家了解如何用冒泡排序实现my_qsort,如果你觉得我写的还不错的话,可以给我一个赞👍吗,感谢❤️ 目录 一. 前言二. 冒泡排序三. 4个参数3.1 第一个参数void* base3.2 第二个参数…...

【css】深入理解flex属性
参考文章: 深入理解Flex属性 flex弹性布局教程-05-项目属性flex-shrink flex:flex-grow flex-shrink flex-basis flex:0 1 0 如何计算flex布局,有flex-shrink和flex-grow的情况下,每个元素的大小 flex-grow生效公式如…...
前端项目开发流程
一 参加需求对称(评审)会议 时间:在产品设计完成以后,进入正式的开发流程之前 组织者:产品&项目经理 目的:统一大家对产品的认识,及时发现产品设计缺陷,尽可能降低后续修改需求的频率 参与者ÿ…...

MybatisPlus逆向工程入门指南:让你的开发更高效、更简洁、更优雅
学会了,可以看看这篇文章:更新中~ 正向工程:先创建Java实体类,由框架负责根据实体类生成数据库表。Hibernate是支持正向工程的。 逆向工程:先创建数据库表,由框架负责根据数据库表,反向生成如下…...

通用商城项目(下)
记录一些踩坑的地方,以及理顺一些思路。 通过管理系统页面,完成商品属性分组和商品属性(基本属性)关联维护 属性表 与 属性组表 的功能完善:显示属性组与属性表的一对多关系 前端 1. 引入组件,是否显示使…...
k8s集群使用ingress转发grafana服务
文章目录 前言一、思路二、grafana准备1. grafana-configmap.yaml2. grafana.yaml 三、ingress准备1. ingress.yaml2. grafana-externalname.yaml3. ingress-nginx-controller 四、 本机host文件准备五、访问测试 前言 在k8s集群中,使用ingress服务转发grafana的页…...

MongoDB的备份和恢复
工具 mongodump 和 mongorestore是MongoDB自带的备份恢复工具。 参考文章 ## https://blog.csdn.net/GUDUzhongliang/article/details/131915625## https://blog.csdn.net/mingongge/article/details/130695422 备份 mongodump 参数 -h, --host<hostname> …...

Pytorch学习笔记(GPU训练)
GUP训练 配置pytorch的gup版本主要是在网络模型、输入和标记的数据、损失函数 方式一 直接.cuda()调用,在原有的模型训练代码中的网络模型、输入和标记的数据、损失函数部分直接调用即可 方式二 事先定义好设备device,然后直接.to(device)调用,在原…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...
