LeetCode 753. 破解保险箱【欧拉回路,DFS】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
有一个需要密码才能打开的保险箱。密码是 n 位数, 密码的每一位都是范围 [0, k - 1] 中的一个数字。
保险箱有一种特殊的密码校验方法,你可以随意输入密码序列,保险箱会自动记住 最后 n 位输入 ,如果匹配,则能够打开保险箱。
- 例如,正确的密码是
"345",并且你输入的是"012345":- 输入
0之后,最后3位输入是"0",不正确。 - 输入
1之后,最后3位输入是"01",不正确。 - 输入
2之后,最后3位输入是"012",不正确。 - 输入
3之后,最后3位输入是"123",不正确。 - 输入
4之后,最后3位输入是"234",不正确。 - 输入
5之后,最后3位输入是"345",正确,打开保险箱。
- 输入
在只知道密码位数 n 和范围边界 k 的前提下,请你找出并返回确保在输入的 某个时刻 能够打开保险箱的任一 最短 密码序列 。
示例 1:
输入:n = 1, k = 2
输出:"10"
解释:密码只有 1 位,所以输入每一位就可以。"01" 也能够确保打开保险箱。
示例 2:
输入:n = 2, k = 2
输出:"01100"
解释:对于每种可能的密码:
- "00" 从第 4 位开始输入。
- "01" 从第 1 位开始输入。
- "10" 从第 3 位开始输入。
- "11" 从第 2 位开始输入。
因此 "01100" 可以确保打开保险箱。"01100"、"10011" 和 "11001" 也可以确保打开保险箱。
提示:
1 <= n <= 41 <= k <= 101 <= k^n <= 4096
保险箱的密码是一个长度为 n n n 的数字字符串,密码中每位数字的取值范围是从 0 0 0 到 k − 1 k-1 k−1 。现在这 n n n 位密码未知,题目要求我们生成一个可以暴力破解这 n n n 位密码的字符串序列 s e q seq seq ,要想用 s e q seq seq 破解密码,那么 s e q seq seq 中必须包含 n n n 位密码的所有组合,最简单的是将 n n n 位密码的 k n k^n kn 个组合拼在一起构成 s e q seq seq ,但这样的 s e q seq seq 太长了,题目要我们生成一个包含 n n n 位密码所有组合情况的一个最短序列。
举个例子, n = 2 , k = 2 n = 2, k = 2 n=2,k=2 ,密码长度为 2 2 2 ,每位数字由 0 0 0 和 1 1 1 组成,那么长度为 2 2 2 的密码就有 k n = 2 2 = 4 k^n = 2^2 = 4 kn=22=4 种组合,即 00 , 01 , 10 , 11 00, 01, 10, 11 00,01,10,11 ,要想破解密码,最简做法是,将这四种密码组合拼在一起组成破解序列 s e q = 00011011 seq = 00011011 seq=00011011 ,这样得到的序列长度为 8 8 8 ,但它不是包含所有密码组合的最短序列。也就是说这种简单拼接在一起的方法,得到的破解序列是冗余的,会增加破解时间。
而密码破解的方法其实就是朴素的字符串匹配,比如上面的 s e q = 00011011 seq = 00011011 seq=00011011 ,依次匹配的子串是 00 , 00 , 01 , 11 , 10 , 01 , 11 00, 00, 01, 11, 10, 01, 11 00,00,01,11,10,01,11 ,一共做了 7 7 7 次密码匹配,其中 00 , 01 , 11 00, 01, 11 00,01,11 分别匹配了两次,也就是说多做了 3 3 3 次冗余的密码匹配。题目要求的 最短破解序列 就是不会产生冗余密码匹配的序列,长度正好是 k n + ( n − 1 ) k^n + (n - 1) kn+(n−1) ,最多只需要匹配 k n k^n kn 次, s e q = 00110 seq = 00110 seq=00110 是上面的其中一个破解序列,长度为 5 5 5 ,依次匹配的子串分别是 00 , 01 , 11 , 10 00, 01, 11, 10 00,01,11,10 ,匹配的正好是所有四种密码组合。
一种建模方式是:对于所有 m = k n m = k^n m=kn 个密码组合,我们把每个 n n n 位可能的密码看成是图中的一个顶点,对于这 m m m 个顶点构成的 完全图 中,让我们找到这样一个回路 v 1 → v 2 → v 3 → . . . → v m → v 1 v_1 \to v_2\to v_3\to ... \to v_m \to v_1 v1→v2→v3→...→vm→v1 ,除起始顶点外每个顶点访问且仅访问一次,其中 < u , v > <u, v> <u,v> 表示回路中一条由顶点 u u u 指向 v v v 的边,且顶点 u u u 长为 n − 1 n-1 n−1 的后缀恰好是顶点 v v v 的前缀。最终我们要的 最短破解序列 ,一种顶点序列是 v 1 , v 2 , v 3 , . . . , v m v_1, v_2, v_3, ..., v_m v1,v2,v3,...,vm ,长度为 k n + ( n − 1 ) k^n + (n - 1) kn+(n−1) ,这个 最短破解序列 不止一个,因为 回路 中的任意一个顶点都可以做 起始顶点。这就是 哈密顿回路问题 。
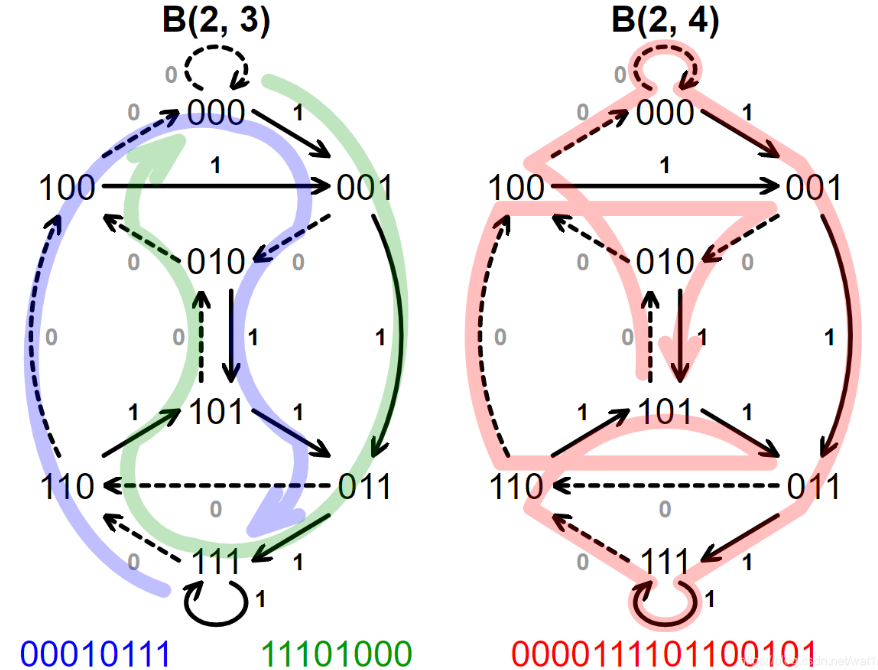
不过查看Wiki,发现本题求的答案有专门的术语 De Bruijn sequence : B ( k , n ) B(k,n) B(k,n) 是 k k k 进制元素构成的循环序列,所有长度为 n n n 的 k k k 进制元素序列都是 B ( k , n ) B(k, n) B(k,n) 的子数组(以环状形式),在 B ( k , n ) B(k,n) B(k,n) 中出现且仅出现一次。
描述该循环序列的图是 De Bruijn 图(一张欧拉图)。使用( n − 1 = 4 − 1 = 3 n - 1 = 4 - 1=3 n−1=4−1=3)3-D De Bruijn 图可以循环构造长度为 2 4 = 16 2^4 = 16 24=16 的 B(2,4) De Bruijn 序列。如下的3维 De Bruijn 图中的每条边对应于一个四位数字的序列:三个数字分别标记该边要离开的顶点,其后是一个数字标记该边。如果一个人从 000 000 000 穿过标记为 1 1 1 的边,则一个人到达 001 001 001 ,从而表明 De Bruijn 序列中存在子序列 0001 0001 0001 。精确遍历每条边一次,就是使用 16 16 16 个四位数序列中的每一个恰好一次。下图,在 B(2,3) 中每个顶点被访问一次,而在 B(2,4) 中每条边(包括自环)都被遍历一次。
解法 Hierholzer \text{Hierholzer} Hierholzer 算法
Hierholzer \text{Hierholzer} Hierholzer 算法可以在一个欧拉图中找出欧拉回路。具体地,我们将所有的 n − 1 n-1 n−1 位数作为节点,共有 k n − 1 k^{n-1} kn−1 个节点,每个节点有 k k k 条入边和出边。如果当前节点对应的数为 a 1 a 2 ⋯ a n − 1 a_1 a_2 \cdots a_{n-1} a1a2⋯an−1 ,那么它的第 x x x 条出边就连向数 a 2 ⋯ a n − 1 x a_2 \cdots a_{n-1} x a2⋯an−1x 对应的节点。这样从一个节点顺着第 x x x 条边走到另一个节点,就相当于输入了数字 x x x 。
在某个节点对应的数的末尾放上它某条出边的编号,就形成了一个 n n n 位数,并且每个节点都能用这样的方式形成 k k k 个 n n n 位数。
例如 k = 4 , n = 3 k=4,n=3 k=4,n=3 时,节点分别为 00 , 01 , 02 , ⋯ , 32 , 33 00,01,02,⋯ ,32,33 00,01,02,⋯ ,32,33 ,每个节点的出边的编号分别为 0 , 1 , 2 , 3 0,1,2,3 0,1,2,3 ,那么 00 00 00 和它的出边形成了 000 , 001 , 002 , 003 000,001,002,003 000,001,002,003 这 4 4 4 个 3 3 3 位数, 32 32 32 和它的出边形成了 320 , 321 , 322 , 323 320,321,322,323 320,321,322,323 这 4 4 4 个 3 3 3 位数。这样共计有 k n − 1 × k = k n k^{n-1} \times k = k^n kn−1×k=kn 个 n n n 位数,恰好就是所有可能的密码。
由于这个图的每个节点都有 k k k 条入边和出边(有向连通图节点度数都为 0 0 0 ),因此它一定存在一个欧拉回路,即可以从任意一个节点开始,一次性不重复地走完所有的边且回到该节点。因此,我们可以用 Hierholzer \text{Hierholzer} Hierholzer 算法找出这条欧拉回路:
- 设起始节点对应的数为 u u u ,欧拉回路中每条边的编号为 x 1 , x 2 , x 3 , ⋯ x_1, x_2, x_3, \cdots x1,x2,x3,⋯ ,那么最终的字符串即为 u x 1 x 2 x 3 ⋯ u u~ x_1 ~ x_2 ~ x_3 \cdots\ u u x1 x2 x3⋯ u
H i e r h o l z e r Hierholzer Hierholzer 算法如下:
- 我们从节点 u u u 开始,任意地经过还未经过的边,直到我们「无路可走」。此时我们一定回到了节点 u u u ,这是因为所有节点的入度和出度都相等。
- 回到节点 u u u 之后,我们得到了一条从 u u u 开始到 u u u 结束的回路,这条回路上仍然有些节点有未经过的出边。从某个这样的节点 v v v 开始,继续得到一条从 v v v 开始到 v v v 结束的回路,再嵌入之前的回路中,即 u → ⋯ → v → ⋯ → u u \to \cdots \to v \to \cdots \to u u→⋯→v→⋯→u
变为 u → ⋯ → v → ⋯ → v → ⋯ → u u\to \cdots \to v \to \cdots \to v \to \cdots \to u u→⋯→v→⋯→v→⋯→u - 以此类推,直到没有节点有未经过的出边,此时我们就找到了一条欧拉回路。
实际的代码编写具有一定的技巧性。
class Solution {
private:int highest, k;string ans;unordered_set<int> rec;void dfs(int node) {for (int x = 0; x < k; ++x) {int nei = node * 10 + x;if (!rec.count(nei)) { // 改为插入边rec.insert(nei);dfs(nei % highest);ans += (x + '0');}}}
public:string crackSafe(int n, int k) {this->highest = pow(10, n - 1);this->k = k;dfs(0); // 从n-1个0出发ans += string(n - 1, '0'); // 返回的路径顺序应该是n-1个0+翻转的ans// 由于是欧拉回路,所以不用翻转,即可直接返回return ans;}
};
但上述写法比较抽象。我们可以这么写:从一个 n − 1 n-1 n−1 长度的全 0 0 0 串出发枚举 k k k 条边,每经过一条边就将其加入到哈希表中,防止重复经过同一条边。
class Solution {
private:string ans;unordered_set<string> edges;void dfs(string &cur, int k) {for (int i = 0; i < k; ++i) {string edge = cur + to_string(i);if (!edges.count(edge)) {edges.insert(edge);string next = edge.substr(1);dfs(next, k);ans += to_string(i);}}}
public:string crackSafe(int n, int k) {string start = string(n - 1, '0');dfs(start, k);ans += start;return ans;}
};
复杂度分析:
- 时间复杂度: O ( n × k n ) O(n \times k^n) O(n×kn) 。
- 空间复杂度: O ( n × k n ) O(n \times k^n) O(n×kn) 。
相关文章:

LeetCode 753. 破解保险箱【欧拉回路,DFS】困难
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
:Fine-tuning、Knowledge Distillation, etc)
深度学习概念(术语):Fine-tuning、Knowledge Distillation, etc
文章目录 1.Fine-tuning (微调)2.Transfer Learning (迁移学习)3.Knowledge Distillation (知识蒸馏)4.Meta Learning (元学习) 这里的相关概念都是基于已有预训练模型,就是模型本身已经训练好,有一定泛化能力。需要“再加工”满足别的任务需求。 进入后…...

tcp_v4_connect函数的解析
源码: int tcp_v4_connect(struct sock *sk, struct sockaddr *uaddr, int addr_len) {// 解析输入的地址结构struct sockaddr_in *usin (struct sockaddr_in *)uaddr;// 获取 TCP 协议栈的全局 death_row 对象struct inet_timewait_death_row *tcp_death_row;// …...

go-channel
设计原理 Go 提及的设计模式就是:不要通过共享内存的方式进行通信,而是应该通过通信的方式共享内存。 共享内存方式:多个协程共享同一块内存,但是多个协程中读写变量是操作同一块内存,会产生多线程问题的并发问题&am…...
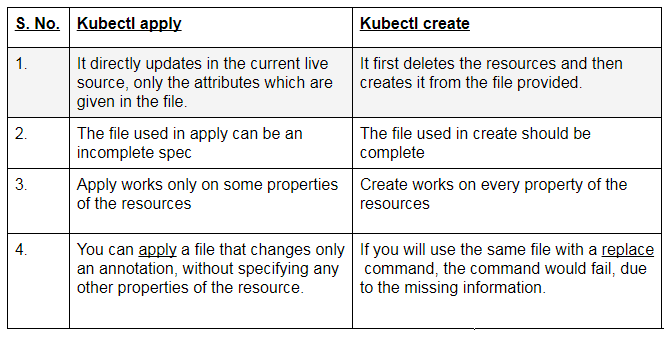
K8s操作命令
生命周期管理 1. 创建 1. 创建资源 kubectl run 创建并运行一个或多个容器镜像。*创建一个deployment或job来管理容器*。 语法:kubectl run NAME --imageimage [–env“keyvalue”] [–portport] [–replicasreplicas] [–dry-runbool] [–overridesinline-jso…...
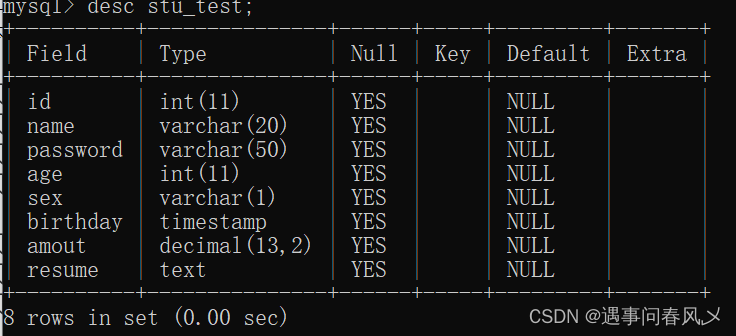
【MySQL】 MySQL数据库基础
文章目录 🐱👓数据库的操作📌显示当前的数据库📌创建数据库🎈语法:🎈语法说明🎈示例: 🌴使用数据库🎋删除数据库🐱🏍语…...
vscode 下载安装
vscode 下载安装常用插件 vscode 官网: https://code.visualstudio.com/ 点击右上角 Download 进入下载选择页面 选择自己使用操作对应 CPU 架构 下载 本文使用 x86 架构 64位 windows 系统为例 跳转下载页面 自动 开始下载 下载不开始?试试这个直…...
springboot对接postgres
安装postgres 注意:下述链接方式会自动创建数据库steven_russell,若需要创建其他数据库,可以手动执行命令创建数据库 docker run --name postgres \ -p 5432:5432 \ -e POSTGRES_USERsteven_russell \ -e POSTGRES_PASSWORD123456 \ -itd --privilegedtrue postgre…...

[python 刷题] 242 Valid Anagram
[python 刷题] 242 Valid Anagram 题目: Given two strings s and t, return true if t is an anagram of s, and false otherwise. An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the o…...
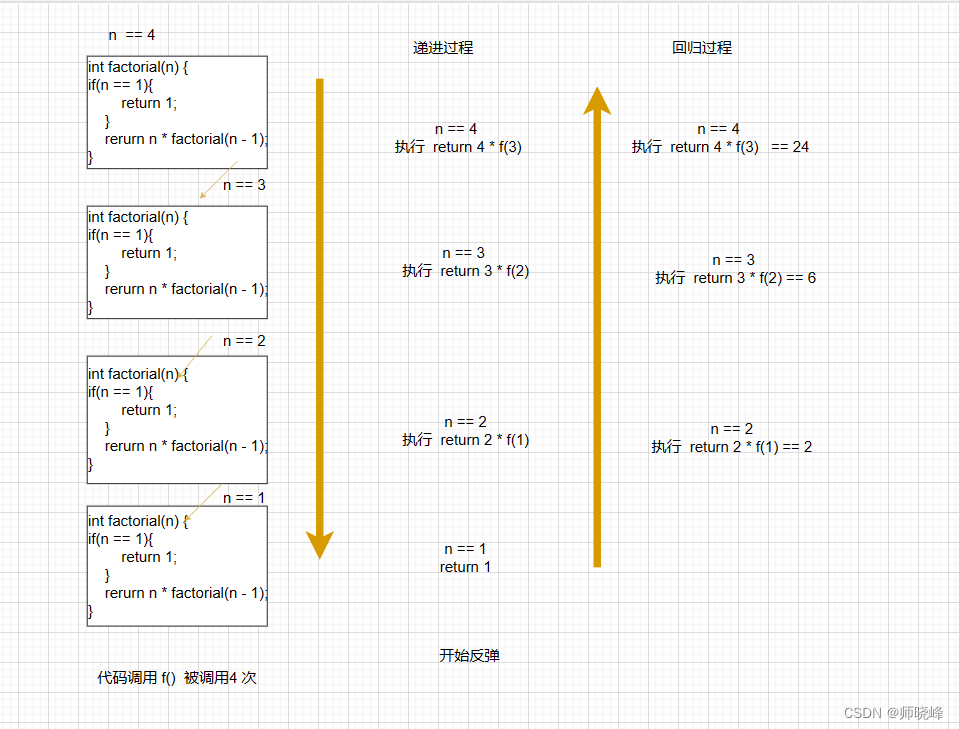
算法通过村第七关-树(递归/二叉树遍历)青铜笔记|手撕递归
文章目录 前言1. 递归的特征2. 如何写出好的递归3. 怎么看懂递归的代码总结 前言 提示:我们生活在24小时不眠不休的社会里但是没有24小时不眠不休的身体有些东西必须舍弃 -- 马特海格 这一关,我看要谈论的是递归问题,说到它就牵扯到很多问题了…...
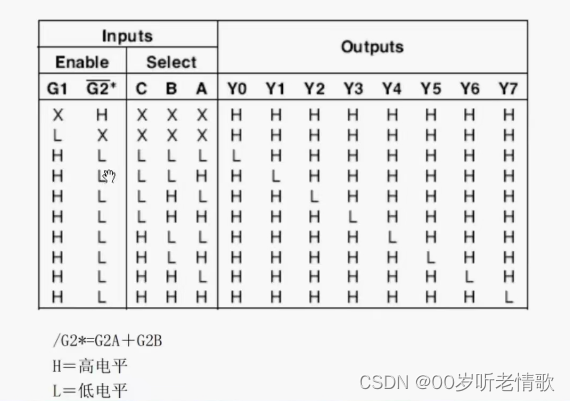
#循循渐进学51单片机#点亮你的LED#not.2
1、深刻理解电容的意义,并且在今后的电路学习过程中要多多注意参考别人电路中去耦电路的处理方法,积累经验。 1)电容缓冲电压,抗电磁干扰; 2)低频率电容,一般用的最多的是钽电容,电…...
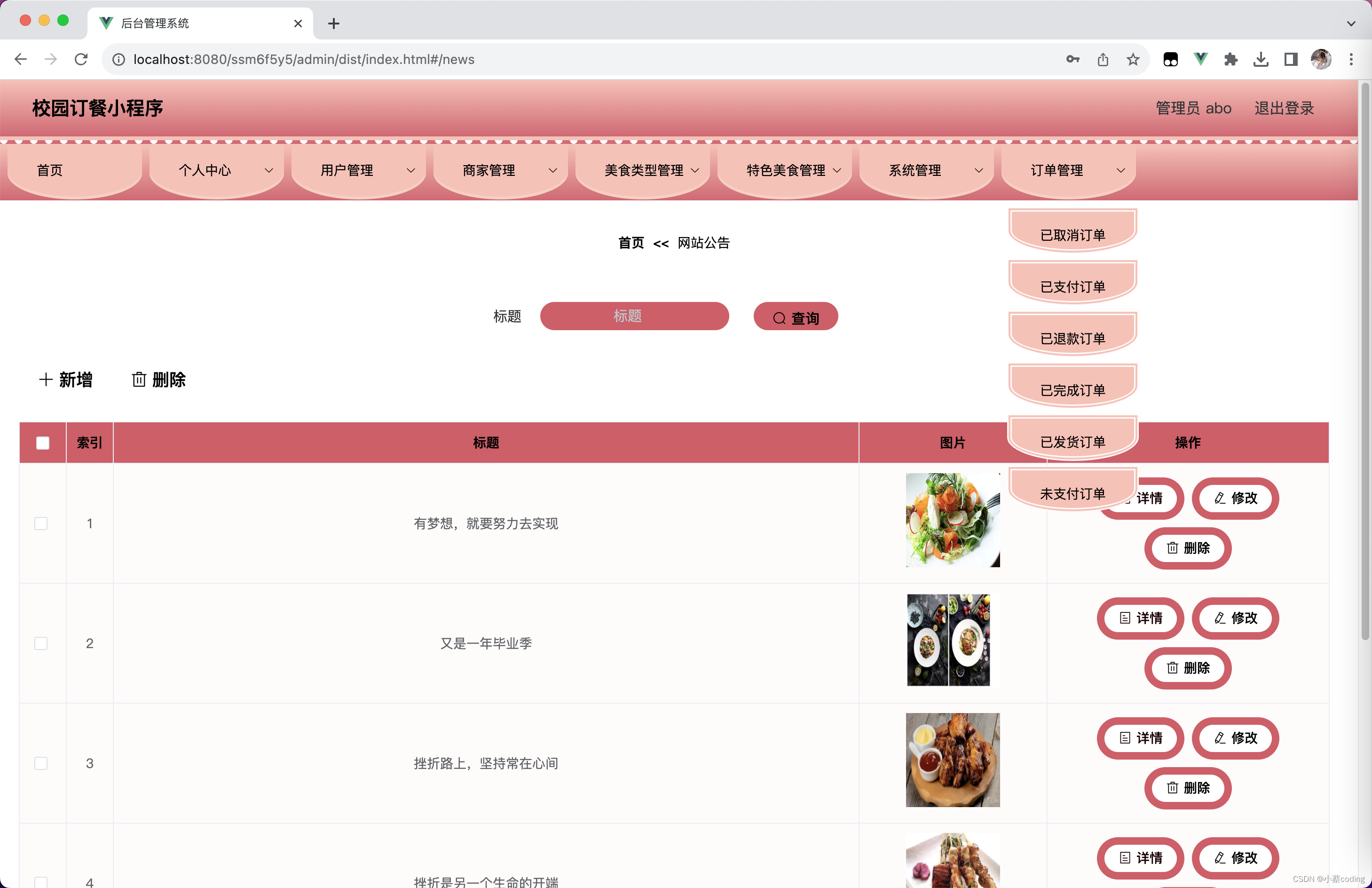
基于Java+SpringBoot+Vue+uniapp点餐小程序(亮点:协同过滤算法、会员系统,购物车结算、在线聊天)
校园点餐小程序 一、前言二、我的优势2.1 自己的网站2.2 自己的小程序(小蔡coding)2.3 有保障的售后2.4 福利 三、开发环境与技术3.1 MySQL数据库3.2 Vue前端技术3.3 Spring Boot框架3.4 微信小程序 四、功能设计4.1 系统功能结构设计4.2 主要功能描述 五…...
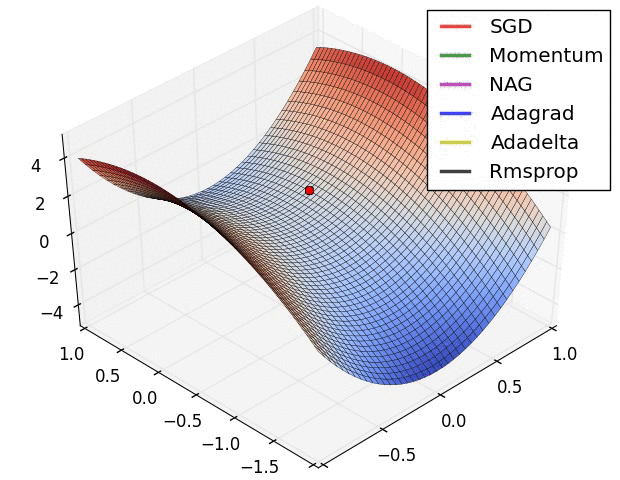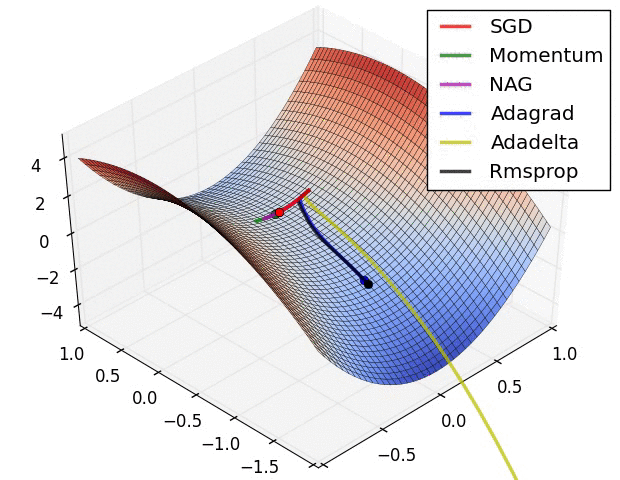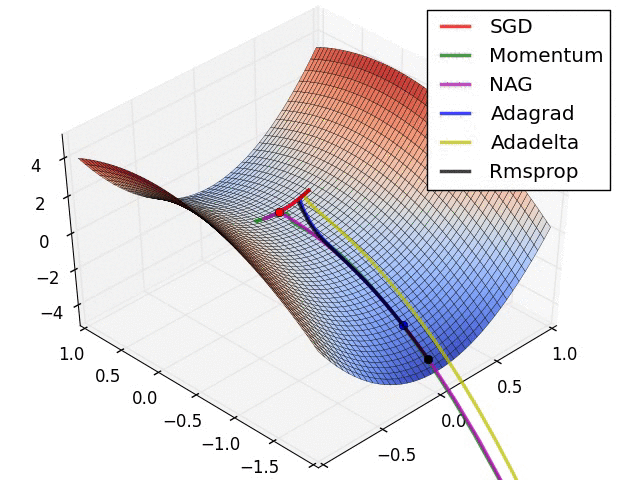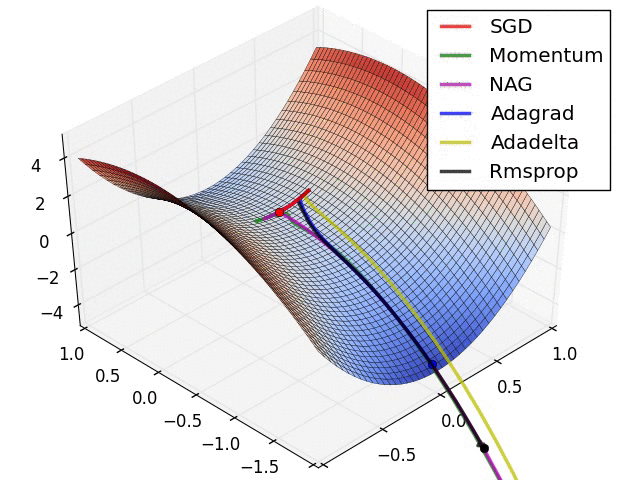
深度学习-全连接神经网络-详解梯度下降从BGD到ADAM - [北邮鲁鹏]
文章目录 参考文章及视频导言梯度下降的原理、过程一、什么是梯度下降?二、梯度下降的运行过程 批量梯度下降法(BGD)随机梯度下降法(SGD)小批量梯度下降法(MBGD)梯度算法的改进梯度下降算法存在的问题动量法(Momentum)目标改进思想为什么有效动量法还有什么效果&…...
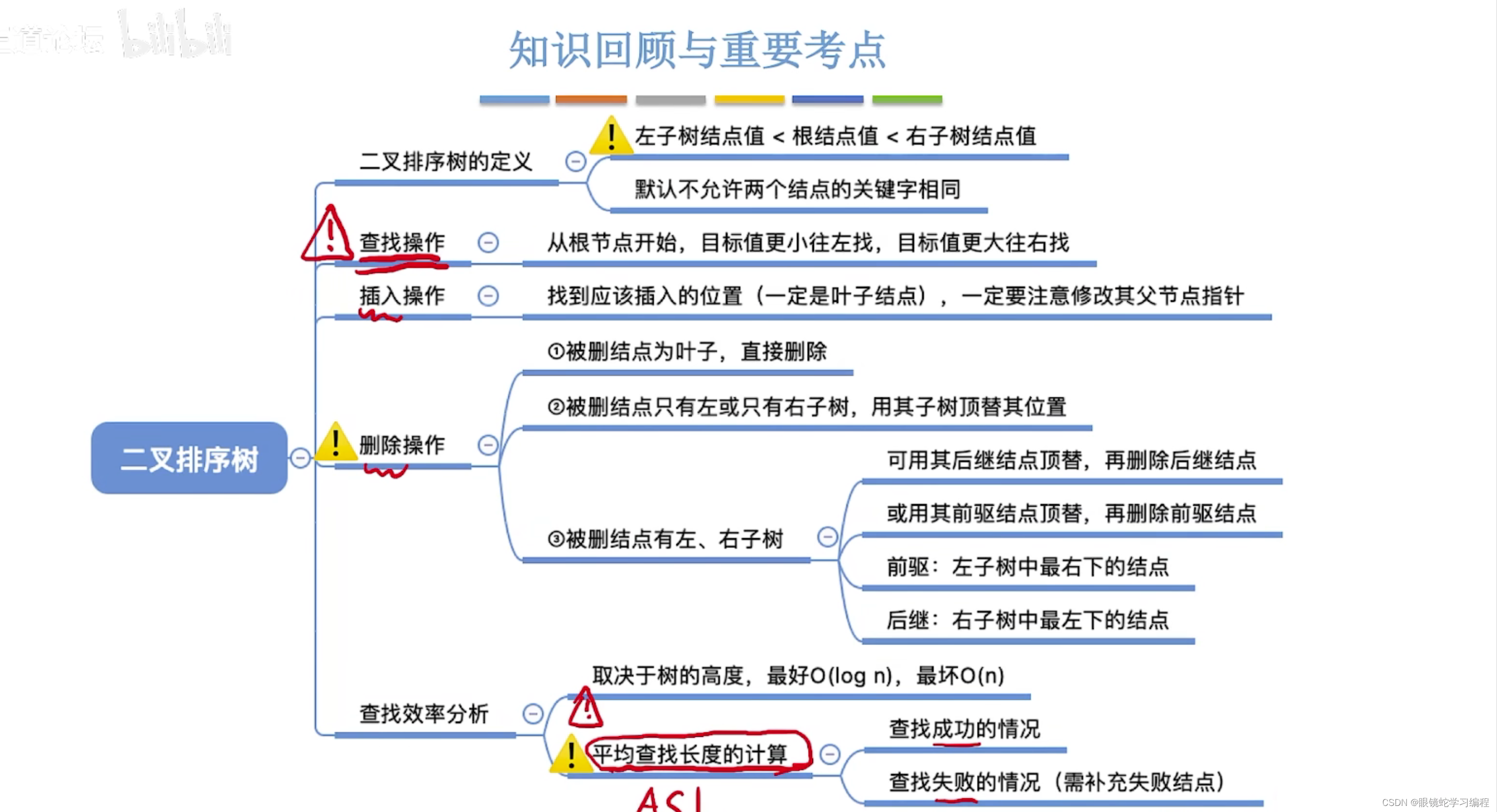
数据结构--二叉排序树
目录 二叉排序树的定义 二叉排序树的查找 二叉排序树的插入 二叉排序树的构造 二叉排序树的删除 查找效率分析 回顾 二叉排序树的定义 二叉排序树的查找 查找成功的情况 查找失败的情况 二叉排序树的插入 注意 (1)二叉排序树不允许出现重复的值…...

Python | 根据子列表中的第二个元素对列表进行排序
在本文中,我们将学习如何根据主列表中存在的子列表的第二个元素对任何列表进行排序。 比如 Input : [[‘rishav’, 10], [‘akash’, 5], [‘ram’, 20], [‘gaurav’, 15]] Output : [[‘akash’, 5], [‘rishav’, 10], [‘gaurav’, 15], [‘ram’, 20]] Input …...

qsort函数详细讲解以及利用冒泡排序模拟实现qsort函数
个人主页:点我进入主页 专栏分类:C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶 C语言刷题 欢迎大家点赞,评论,收藏。 一起努力,一起奔赴大厂。 目录 1.qsort函数 1.1qsort函数的参数 …...

C++QT day6
1> 将之前定义的栈类和队列类都实现成模板类 栈: #include <iostream> #define MAX 128 using namespace std; template<typename T> class Stack_s { private:T *pnew T[MAX];//栈的数组int top;//记录栈顶的变量 public://构造函数Stack_s(int t…...
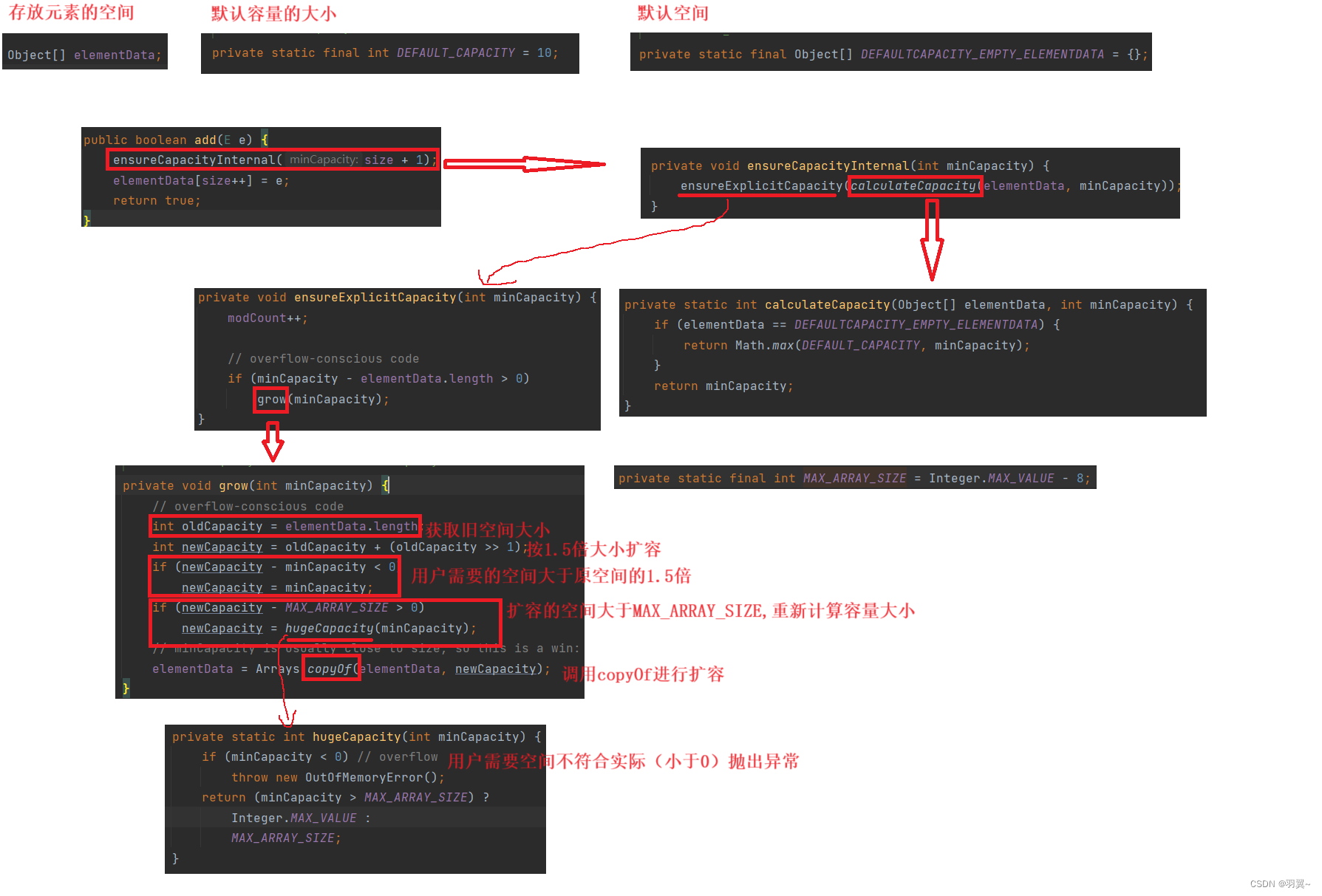
List与ArrayList
目录 一、List及其使用 1.1 List的概念 1.2 常见接口的介绍 1.3 List的使用 二、线性表和顺序表 2.1 线性表 2.2 顺序表 三、ArrayList介绍 四、ArrayList的使用 4.1 ArrayList构造 4.2 ArrayList的常用方法 4.3 ArrayList的遍历 4.4 ArrayList的扩容机制 五、ArrayList的具…...
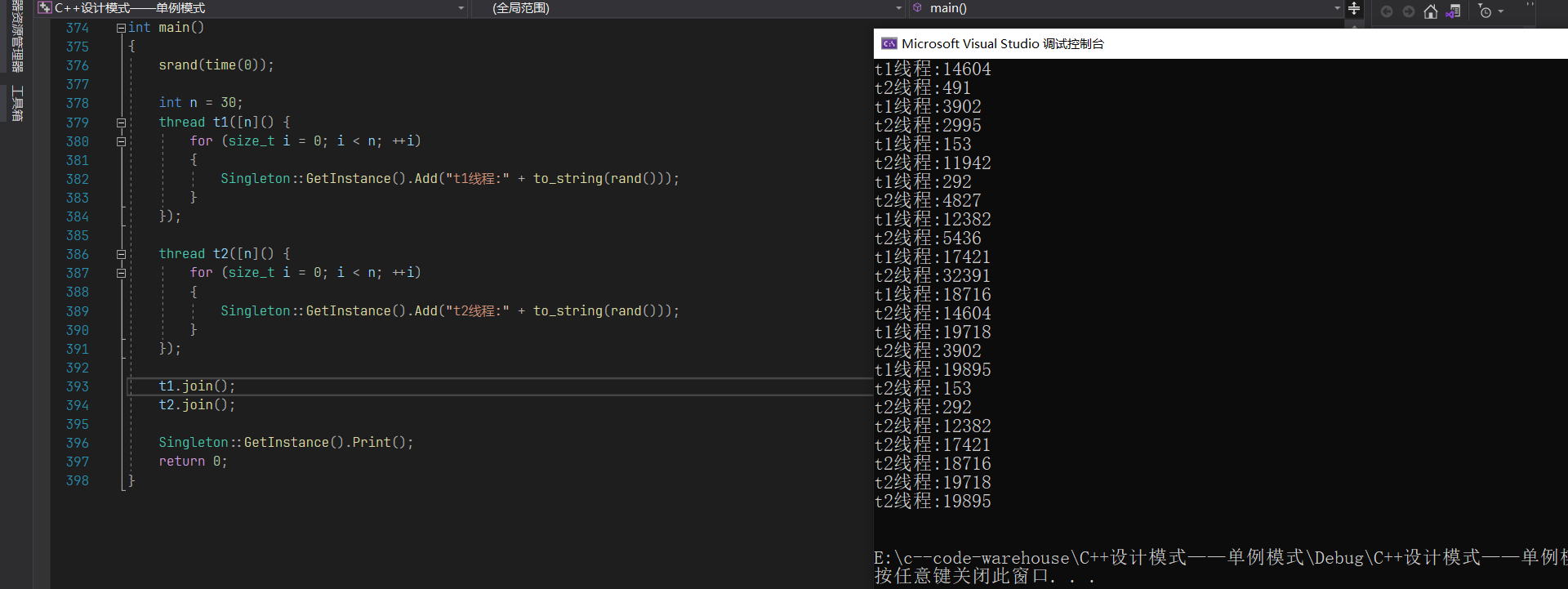
【C++】特殊类的设计
文章目录 1. 设计一个类, 不能被拷贝2. 设计一个类, 不能被继承3. 设计一个类, 只能在堆上创建对象3. 设计一个类, 只能在栈上创建对象4. 创建一个类, 只能创建一个对象(单例模式)饿汉模式懒汉模式 1. 设计一个类, 不能被拷贝 💕 C98方式: 在C11之前&a…...
机器学习:PCA(Principal Component Analysis主成分)降维
参考:PCA降维原理 操作步骤与优缺点_TranSad的博客-CSDN博客 PCA降维算法_偶尔努力翻身的咸鱼的博客-CSDN博客 需要提前了解的数学知识: 一、PCA的主要思想 PCA,即主成分分析方法,是一种使用最广泛的数据降维算法。PCA的主要思想…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...
