蓝桥杯2023年第十四届省赛真题-更小的数--题解
目录
蓝桥杯2023年第十四届省赛真题-更小的数
题目描述
输入格式
输出格式
样例输入
样例输出
提示
【思路解析】
【代码实现】
蓝桥杯2023年第十四届省赛真题-更小的数
时间限制: 3s 内存限制: 320MB 提交: 895 解决: 303
题目描述
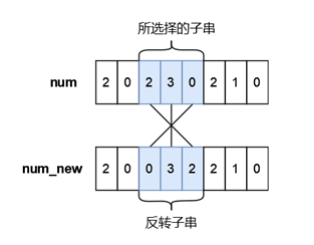
小蓝有一个长度均为 n 且仅由数字字符 0 ∼ 9 组成的字符串,下标从 0 到 n − 1,你可以将其视作是一个具有 n 位的十进制数字 num,小蓝可以从 num 中选出一段连续的子串并将子串进行反转,最多反转一次。小蓝想要将选出的子串进行反转后再放入原位置处得到的新的数字 numnew 满足条件 numnew < num,请你帮他计算下一共有多少种不同的子串选择方案,只要两个子串在 num 中的位置不完全相同我们就视作是不同的方案。
注意,我们允许前导零的存在,即数字的最高位可以是 0 ,这是合法的。
输入格式
输入一行包含一个长度为 n 的字符串表示 num(仅包含数字字符 0 ∼ 9),
从左至右下标依次为 0 ∼ n − 1。
输出格式
输出一行包含一个整数表示答案。
样例输入
复制
210102
样例输出
复制
8
提示
一共有 8 种不同的方案:
1)所选择的子串下标为 0 ∼ 1 ,反转后的 numnew = 120102 < 210102 ;
2)所选择的子串下标为 0 ∼ 2 ,反转后的 numnew = 012102 < 210102 ;
3)所选择的子串下标为 0 ∼ 3 ,反转后的 numnew = 101202 < 210102 ;
4)所选择的子串下标为 0 ∼ 4 ,反转后的 numnew = 010122 < 210102 ;
5)所选择的子串下标为 0 ∼ 5 ,反转后的 numnew = 201012 < 210102 ;
6)所选择的子串下标为 1 ∼ 2 ,反转后的 numnew = 201102 < 210102 ;
7)所选择的子串下标为 1 ∼ 4 ,反转后的 numnew = 201012 < 210102 ;
8)所选择的子串下标为 3 ∼ 4 ,反转后的 numnew = 210012 < 210102 ;
对于 20% 的评测用例,1 ≤ n ≤ 100 ;
对于 40% 的评测用例,1 ≤ n ≤ 1000 ;
对于所有评测用例,1 ≤ n ≤ 5000 。
【思路解析】
遍历所有可能性,对于一个子串 i -- j,有3种情况。
(1)如果str[i] > str[j],可以交换。
(2) 如果str[i] < str[j],不可以交换。
(3)如果str[i] == str[j],则考虑 子串 i+1 --- j-1,可不可以被交换,如果可以交换,则原子串可以交换,否则不可以被交换。
【代码实现】
import java.util.Scanner;/*** @ProjectName: study3* @FileName: Ex2* @author:HWJ* @Data: 2023/9/17 9:22*/
public class Ex2 {static int ans = 0;public static void main(String[] args) {Scanner input = new Scanner(System.in);String s = input.next();char[] str = s.toCharArray();for (int right = 1; right < str.length; right++) {for (int left = 0; left < right; left++) {int L = left + 1;int R = right - 1;boolean loop = false;while (L < R){if(str[L] > str[R]){loop = true;break;} else if (str[L] < str[R]) {break;}else {L += 1;R -= 1;}}if (str[left] > str[right] || (loop && str[left] == str[right])){ans++;}}}System.out.println(ans);}}相关文章:

蓝桥杯2023年第十四届省赛真题-更小的数--题解
目录 蓝桥杯2023年第十四届省赛真题-更小的数 题目描述 输入格式 输出格式 样例输入 样例输出 提示 【思路解析】 【代码实现】 蓝桥杯2023年第十四届省赛真题-更小的数 时间限制: 3s 内存限制: 320MB 提交: 895 解决: 303 题目描述 小蓝有一个长度均为 n 且仅由数字…...

SpringBoot详解
文章目录 SpringBoot的特点Spring,SpringBoot的区别SpringBoot常用注解标签SpringBoot概述SpringBoot简单Demo搭建读取配置文件的内容 SpringBoot自动配置Condition自定义beanSpringBoot常用注解原理EnableAutoConfiguration SpringBoot监听机制SpringBoot启动流程分…...

typescript 类型断言
typescript 类型断言 TypeScript 是一种在 JavaScript 基础上开发的强类型语言,它为开发者提供了类型安全性和其他有用的特性。类型断言是 TypeScript 中的一种特性,允许开发者在编译时确定变量或表达式的类型。类型断言有多种使用场景,包括…...

如何确定自己是否适合做程序员?
如果你不确定你是否注定要成为一名程序员,这里有六个迹象可能表明你不适合。 1. 你缺乏实验创造力 尽管编程的基础是逻辑,但它在很大程度上是一种创造性的艺术。新程序就像一张空白的画布。画笔和调色板是语言、框架和库。您需要对自己的创作和创造力有…...
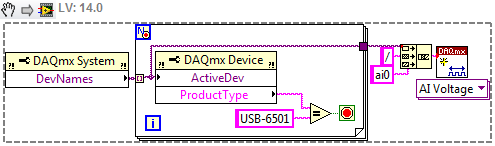
LabVIEW以编程方式查找系统中DAQ设备的设备名称
LabVIEW以编程方式查找系统中DAQ设备的设备名称 使用DAQmx VI,“创建虚拟通道”函数,这个函数需要物理通道输入端。当使用相同型号的新设备(例如,两个不同的USB-6210)运行可执行文件时,代码会中断…...

23、mysql数据库的安装
(无图,简易版本) 一、下载 点开下面的链接:https://dev.mysql.com/downloads/mysql/ 点击Download 就可以下载对应的安装包了 二、解压 下载完成后我们得到的是一个压缩包,将其解压,我们就可以得到MyS…...

【实战详解】如何快速搭建接口自动化测试框架?Python + Requests
摘要: 本文主要介绍如何使用Python语言和Requests库进行接口自动化测试,并提供详细的代码示例和操作步骤。希望能对读者有所启发和帮助。 前言 随着移动互联网的快速发展,越来越多的应用程序采用Web API(也称为RESTful API&…...

Linux安全加固:保护你的服务器
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

【C++初阶】C++STL详解(四)—— vector的模拟实现
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:C初阶 🎯长路漫漫浩浩,万事皆有期待 【C初阶】CSTL详解(三…...

VS code 下 makefile 【缺少分隔符 停下来】 报错解决方法
首先来看报错的makefile源码 再来看报错的信息: 第5行缺少分隔符,其实不止是第5行,只要是前面需要加tab留白的行都会报这个错误,比如说第7行第11行 编译的时候,前面的留白必须是按tab键生成的 但是!&…...

虹科案例 | Zuellig Pharma和ELPRO通过符合GDP标准的温度监测和高效的温度数据管理为未来发展奠定基础
在本案例研究中,您将了解Zuellig Pharma 实施了温度监测解决方案,以一致的数据结构获取各国和各种运输方式的数据; 通过将温度数据上传到其数据库管理系统,显著提高了其效率; 并建立了为未来管理决策提供数据增值使用的基础。 项目合作伙伴 …...

为啥我的第二个for循环不加框红的代码就运行失效呢?(文末赠书)
点击上方“Python爬虫与数据挖掘”,进行关注 回复“书籍”即可获赠Python从入门到进阶共10本电子书 今 日 鸡 汤 苟全性命于乱世,不求闻达于诸侯。 大家好,我是皮皮。 一、前言 前几天在Python最强王者群【哎呦喂 是豆子~】问了一…...

Java高级之注解
文章目录 一、注解1.1、Annotation的使用示例1.2、自定义注解1.3、元注解1.4、通过反射获取注解信息---未完成1.5、jdk 8 中注解的新特性 一、注解 注解:Annotation 注解是一种趋势,一定程度上 可以说:框架 注解 反射 设计模式 jdk 5.0 新…...
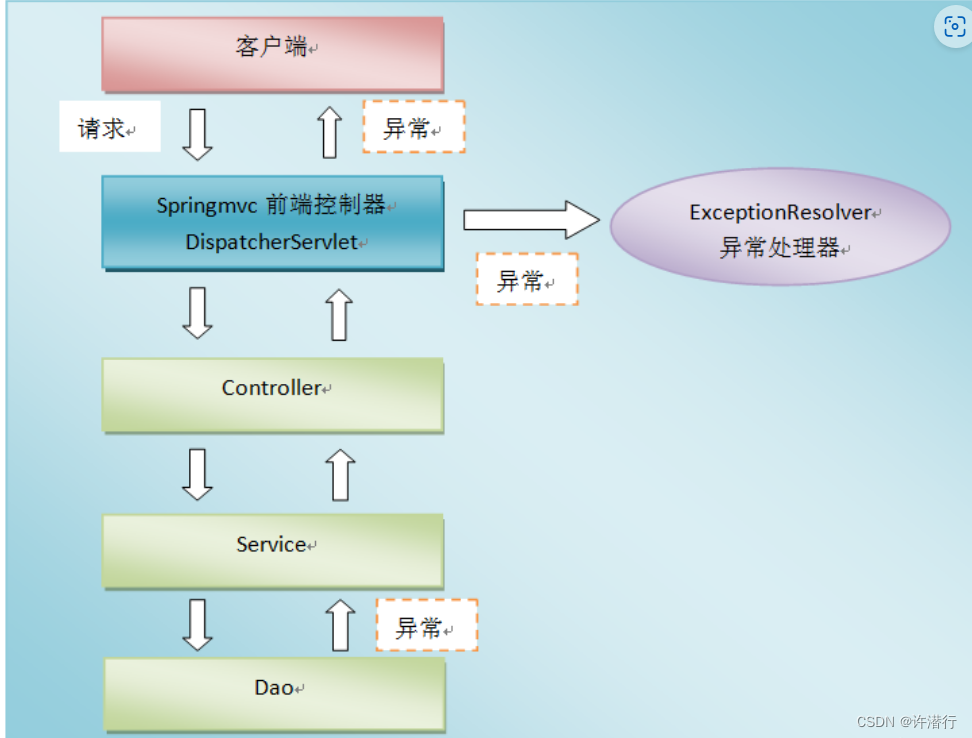
【SpringMVC】JSON数据传输与异常处理的使用
文章目录 一、Jackson1.1 Jackson是什么1.2 常用注解1.3 实例1.3.1导入依赖1.3.2 配置spring-mvc.xml1.3.3 JsonController.java 二、Spring MVC异常处理机制2.1 使用原因2.2 SpringMVC异常处理2.2.1 异常处理机制流程图2.2.2 异常处理的三种方式 一、Jackson 1.1 Jackson是什…...
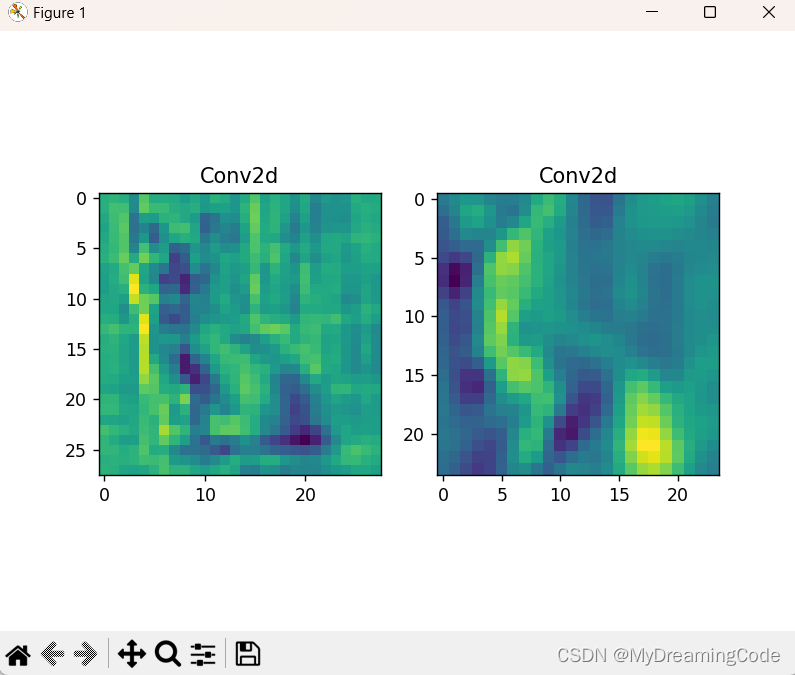
LeNet-5
目录 一、知识点 二、代码 三、查看卷积层的feature map 1. 查看每层信息 2. show_featureMap.py 背景:LeNet-5是一个经典的CNN,由Yann LeCun在1998年提出,旨在解决手写数字识别问题。 一、知识点 1. iter()next() iter():…...

Anaconda bug
报错如下: DEBUG:urllib3.connectionpool:Starting new HTTPS connection (1): repo.anaconda.com:443 DEBUG:urllib3.connectionpool:Starting new HTTPS connection (1): repo.anaconda.com:443 DEBUG:urllib3.connectionpool:Starting new HTTPS connection (1):…...

xen-trap
Xen-Trap xen的虚拟化实现有一个很重要的机制就是tarp,中文可以暂且叫做陷入。在ARMv8中,trap就是异常等级的一个切换。 当发生trap的时候,就会进入设定好的异常向量表中,硬件自动判断属于哪种类型的异常。 一、异常处理 ARM…...

微服务架构介绍
系统架构的演变 1、技术架构发展历史时间轴 ①单机垂直拆分:应用间进行了解耦,系统容错提高了,也解决了独立应用发布的问题,存在单机计算能力瓶颈。 ②集群化负载均衡可有效解决单机情况下并发量不足瓶颈。 ③服务改造架构 虽然系…...
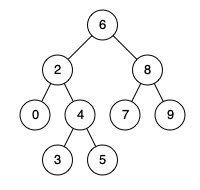
235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己…...
DETR:End-to-End Object Detection with Transformers
代码:https://github.com/HuKai97/detr-annotations 论文:https://arxiv.org/pdf/2005.12872.pdf 参考视频:DETR 论文精读【论文精读】_哔哩哔哩_bilibili 团队:Meta AI 摘要 DETR 做目标检测任务既不需要proposal࿰…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...

智能照明系统:具备认知能力的“光神经网络”
智能照明系统是物联网技术与传统照明深度融合的产物,其本质是通过感知环境、解析需求、自主决策的闭环控制,重构光与人、空间、环境的关系。这一系统由智能光源、多维传感器、边缘计算单元及云端管理平台构成,形成具备认知能力的“光神经网络…...

基于微信小程序的作业管理系统源码数据库文档
作业管理系统 摘 要 随着社会的发展,社会的方方面面都在利用信息化时代的优势。互联网的优势和普及使得各种系统的开发成为必需。 本文以实际运用为开发背景,运用软件工程原理和开发方法,它主要是采用java语言技术和微信小程序来完成对系统的…...

Ubantu-Docker配置最新镜像源250605
尝试其他镜像加速器 阿里云镜像加速器:登录阿里云,进入容器镜像服务获取专属加速器地址。毫秒镜像:https://docker.1ms.run。DockerHub镜像加速器:https://docker.xuanyuan.me。Docker Hub 镜像加速服务:https://dock…...
