六、数学建模之插值与拟合
1.概念
2.例题和matlab代码求解
一、概念
1.插值
(1)定义:插值是数学和统计学中的一种技术,用于估算在已知数据点之间的未知数据点的值。插值的目标是通过已知数据点之间的某种函数或方法来估计中间位置的数值。插值通常用于数据分析、图形绘制、数值模拟和其他领域。
(2)常见插值方法
1)线性插值: 是通过已知数据点之间的直线来估算中间位置的值。这意味着在两个相邻的数据点之间,估计值按照线性关系进行插值。
2)多项式插值: 使用多项式函数来逼近已知数据点。最常见的多项式插值方法是Lagrange插值和Newton插值。
3)样条插值: 将数据分段拟合成多项式,通常是低次数的多项式,以确保在相邻区间内的平滑连接。这有助于避免插值函数的过度振荡。
4)三角函数插值: 使用三角函数(如三角多项式或三角样条)来逼近已知数据点。这在周期性数据的插值中特别有用。
5)立方样条插值: 是一种非常流行的方法,它使用三次多项式在相邻数据点之间进行插值,并确保在数据点处有连续的一阶和二阶导数。这使得插值函数在插值区间内非常平滑。
补:
1.拉格朗日多项式插值是一种常用的插值方法,用于估算一组已知数据点之间的未知数据点的值。这个方法使用一个拉格朗日多项式,来逼近数据点。该多项式在每个已知数据点上都经过并且在其他点上为零。这样的多项式可以表示为:

优点是它对数据点的拟合非常精确,它会经过每个数据点。
缺点是随着数据点数量的增加,计算和插值多项式的复杂度会增加。此外,拉格朗日插值在极端情况下可能会导致插值多项式的振荡。

编写一个名为 lagrange.m 的 M 文件
function y=lagrange(x0,y0,x);
n=length(x0);m=length(x);
for i=1:m z=x(i); s=0.0; for k=1:n p=1.0; for j=1:n if j~=k p=p*(z-x0(j))/(x0(k)-x0(j)); end end s=p*y0(k)+s; end y(i)=s;
end
2.牛顿插值用于估算一组已知数据点之间的未知数据点的值。这个方法使用一个牛顿多项式,来逼近数据点。该多项式在每个已知数据点上都经过,并且通过递推方式添加新的数据点来构建多项式。

牛顿插值的优点之一是它可以在添加新的数据点时轻松更新插值多项式,而不需要重新计算整个多项式。
基本步骤

牛顿插值方法通常比拉格朗日插值更有效率,因为它的计算可以逐步进行,而不需要计算大量的基函数。但与其他插值方法一样,牛顿插值的精确性也受到数据点的选择和密度的影响。
3.分段线性插值它将数据点分成若干段,并在每个段内使用线性插值来逼近数据点。这种方法通常用于处理数据在不同区间内具有不同趋势或变化的情况。分段线性插值的目标是在每个段内获得一个近似线性的插值函数,以更好地描述数据。
Matlab 中有现成的一维插值函数 interp1
y=interp1(x0,y0,x,'method') method 指定插值的方法,默认为线性插值。其值可为:
'nearest' 最近项插值
'linear' 线性插值
'spline' 逐段 3 次样条插值
'cubic' 保凹凸性 3 次插值。
所有的插值方法要求 x0 是单调的。
当 x0 为等距时可以用快速插值法,使用快速插值法的格为'*nearest'、'*linear'、'*spline'、'*cubic'。
4.Hermite 插值
如果对插值函数,不仅要求它在节点处与函数同值,而且要求它与函数有相同的一阶、二阶甚至更高阶的导数值,这就是 Hermite 插值问题。
用 Matlab 实现 Hermite 插值
function y=hermite(x0,y0,y1,x);
n=length(x0);m=length(x);
for k=1:m yy=0.0; for i=1:n h=1.0; a=0.0; for j=1:n if j~=i h=h*((x(k)-x0(j))/(x0(i)-x0(j)))^2; a=1/(x0(i)-x0(j))+a; end end yy=yy+h*((x0(i)-x(k))*(2*a*y0(i)-y1(i))+y0(i)); end y(k)=yy;
end
5.样条插值
许多工程技术中提出的计算问题对插值函数的光滑性有较高要求,如飞机的机翼外形,内燃机的进、排气门的凸轮曲线,都要求曲线具有较高的光滑程度,不仅要连续,而且要有连续的曲率,这就导致了样条插值的产生。
Matlab 中三次样条插值也有现成的函数
y=interp1(x0,y0,x,'spline');y=spline(x0,y0,x);pp=csape(x0,y0,conds),y=ppval(pp,x)
其中 x0,y0 是已知数据点,x 是插值点,y 是插值点的函数值对于三次样条插值,我们提倡使用函数 csape,csape 的返回值是 pp 形式,要求插值点的函数值,必须调用函数 ppval。pp=csape(x0,y0):使用默认的边界条件,即 Lagrange 边界条件。
pp=csape(x0,y0,conds)中的 conds 指定插值的边界条件,其值可为:
'complete' 边界为一阶导数,即默认的边界条件
'not-a-knot' 非扭结条件
'periodic' 周期条件
'second' 边界为二阶导数,二阶导数的值[0, 0]。
'variational' 设置边界的二阶导数值为[0,0]。对于一些特殊的边界条件,可以通过 conds 的一个1×2 矩阵来表示,conds 元素的取值为 1,2。此时,使用命令pp=csape(x0,y0_ext,conds)
其中 y0_ext=[left, y0, right],这里 left 表示左边界的取值,right 表示右边界的取值。conds(i)=j 的含义是给定端点i 的 j 阶导数,即 conds 的第一个元素表示左边界的条件,第二个元素表示右边界的条件,conds=[2,1]表示左边界是二阶导数,右边界是一阶导数,对应的值由 left 和 right 给出。详细情况请使用帮助 help csape。
2.拟合
(1)定义:拟合(Fitting)是一种数学和统计方法,用于找到一个数学模型或函数,可以最好地描述或逼近一组观测数据点。拟合的目标是找到一个函数或模型,使其与实际观测值之间的差距最小化,从而能够用来预测、分析或解释数据。
(2)常见的拟合方法
1)线性拟合: 当数据似乎遵循线性关系时,可以使用线性回归来进行拟合。线性回归寻找一条直线,使得该直线与数据点之间的残差平方和最小化。
2)多项式拟合: 多项式拟合使用多项式函数来逼近数据。可以选择不同次数的多项式来获得更高阶或更低阶的拟合。
3)非线性拟合: 当数据与非线性模型更匹配时,可以使用非线性拟合方法,例如非线性回归。这些方法尝试找到一个非线性函数,以最好地拟合数据。
4)指数拟合: 用于模拟数据遵循指数函数的情况,通常用于描述增长或衰减过程。
5)对数拟合: 适用于数据与对数函数之间的关系,通常用于分析指数增长或对数周期性数据。
6)曲线拟合: 是一种通用方法,可以拟合各种不同形状的曲线,例如正弦曲线、高斯曲线等。
7)统计拟合: 在统计学中,拟合可以使用最大似然估计或贝叶斯方法来拟合参数化模型,以最好地描述观测数据的分布。
8)核心拟合: 在机器学习和模式识别中,核心方法(如支持向量机)可用于拟合数据并生成分类或回归模型。
补:
1.线性最小二乘法(Linear Least Squares Method)是一种常用的统计和数学方法,用于拟合一个线性模型,以最小化观测数据点与模型预测值之间的残差平方和。这个方法通常用于回归分析,其中目标是找到一个线性模型,以最好地描述因变量和自变量之间的关系。
二、例题
1 机床加工
待加工零件的外形根据工艺要求由一组数据(x, y) 给出(在平面情况下),用程控铣床加工时每一刀只能沿 x 方向和 y 方向走非常小的一步,这就需要从已知数据得到加工所要求的步长很小的(x, y) 坐标。表 1 中给出的 x, y 数据位于机翼断面的下轮廓线上,假设需要得到 x 坐标每改变0.1 时的 y 坐标。试完成加工所需数据,画出曲线,并求出 x = 0 处的曲线斜率和13 ≤ x ≤ 15 范围内 y 的最小值。

要求用 Lagrange、分段线性和三次样条三种插值方法计算。
matlab代码需要用到之前写好的函数调用
clc,clear
x0=[0 3 5 7 9 11 12 13 14 15];
y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];
x=0:0.1:15;
y1=lagrange(x0,y0,x); %调用前面编写的Lagrange插值函数
y2=interp1(x0,y0,x);
y3=interp1(x0,y0,x,'spline');
pp1=csape(x0,y0); y4=ppval(pp1,x);
pp2=csape(x0,y0,'second'); y5=ppval(pp2,x);
fprintf('比较一下不同插值方法和边界条件的结果:\n')
fprintf('x y1 y2 y3 y4 y5\n')
xianshi=[x',y1',y2',y3',y4',y5'];
fprintf('%f\t%f\t%f\t%f\t%f\t%f\n',xianshi')
subplot(2,2,1), plot(x0,y0,'+',x,y1), title('Lagrange')
subplot(2,2,2), plot(x0,y0,'+',x,y2), title('Piecewise linear')
subplot(2,2,3), plot(x0,y0,'+',x,y3), title('Spline1')
subplot(2,2,4), plot(x0,y0,'+',x,y4), title('Spline2')
dyx0=ppval(fnder(pp1),x0(1)) %求x=0处的导数
ytemp=y3(131:151);
index=find(ytemp==min(ytemp));
xymin=[x(130+index),ytemp(index)]
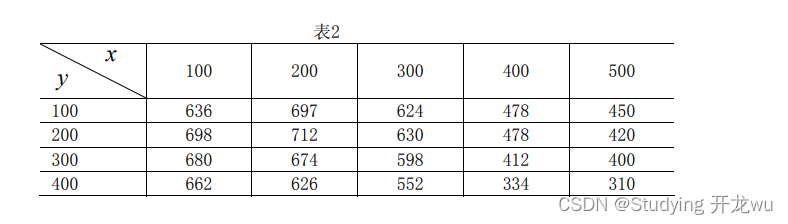
例2 在一丘陵地带测量高程,x 和 y 方向每隔100米测一个点,得高程如2表,试插
值一曲面,确定合适的模型,并由此找出最高点和该点的高程。
clear,clc
x=100:100:500;
y=100:100:400;
z=[636 697 624 478 450 698 712 630 478 420
680 674 598 412 400 662 626 552 334 310];
pp=csape({x,y},z')
xi=100:10:500;yi=100:10:400
cz1=fnval(pp,{xi,yi})
cz2=interp2(x,y,z,xi,yi','spline')
[i,j]=find(cz1==max(max(cz1)))
x=xi(i),y=yi(j),zmax=cz1(i,j)
例 3 在某海域测得一些点(x,y)处的水深 z 由下表给出,在矩形区域(75,200)
×(-50,150) 内画出海底曲面的图形。

x=[129 140 103.5 88 185.5 195 105 157.5 107.5 77 81 162 162 117.5];
y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5];
z=-[4 8 6 8 6 8 8 9 9 8 8 9 4 9];
xi=75:1:200;
yi=-50:1:150;
zi=griddata(x,y,z,xi,yi','cubic')
subplot(1,2,1), plot(x,y,'*')
subplot(1,2,2), mesh(xi,yi,zi)
例4 用最小二乘法求一个形如 y = a + bx^2 的经验公式,使它与表 4 所示的数据
拟合

x=[19 25 31 38 44]';
y=[19.0 32.3 49.0 73.3 97.8]';
r=[ones(5,1),x.^2];
ab=r\y
x0=19:0.1:44;
y0=ab(1)+ab(2)*x0.^2;
plot(x,y,'o',x0,y0,'r')
例 5 某乡镇企业 1990-1996 年的生产利润如表 5,试预测 1997 年和 1998 年的利润。

编写程序如下:
x0=[1990 1991 1992 1993 1994 1995 1996];
y0=[70 122 144 152 174 196 202];
a=polyfit(x0,y0,1)
y97=polyval(a,1997)
y98=polyval(a,1998) 求得 a1 = 20,a0 = −4.0705×10 ,
1997 年的生产利润 y97=233.4286,1998 年的生产利润 y98=253.9286。
相关文章:

六、数学建模之插值与拟合
1.概念 2.例题和matlab代码求解 一、概念 1.插值 (1)定义:插值是数学和统计学中的一种技术,用于估算在已知数据点之间的未知数据点的值。插值的目标是通过已知数据点之间的某种函数或方法来估计中间位置的数值。插值通常用于数…...

【项目经验】:elementui表格中数字汉字排序问题及字符串方法localeCompare()
一.需求 表格中数字汉字排序,数字按大小排列,汉字按拼音首字母(A-Z)排序。 二.用到的方法 第一步:把el-table-column上加上sortable"custom" <el-table-column prop"date" label"序号…...

Spring Boot的运行原理
Spring Boot的运行原理 Spring Boot是一个用于快速构建独立、可独立运行的Spring应用程序的框架。它通过自动配置和约定优于配置的原则,简化了Spring应用程序的开发过程。下面将详细介绍Spring Boot的运行原理,并附上一些代码解释。 1. 主要组件 Sprin…...

xen-gic初始化流程
xen-gic初始化流程 调试平台使用的是gic-600,建议参考下面的文档来阅读代码,搞清楚相关寄存器的功能。 《corelink_gic600_generic_interrupt_controller_technical_reference_manual_100336_0106_00_en》 《IHI0069H_gic_architecture_specification》…...

Docker从认识到实践再到底层原理(六-1)|Docker容器基本介绍+命令详解
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总 然后就是博主最近最花时间的一个专栏…...

【Flink】FlinkCDC自定义反序列化器
在我们用FlinkCDC采集mysql数据(或其他数据源)的时候,FlinkCDC输出的格式不标准,不利于我们后续做数据处理,我们通常会使用自定义反序列化器来格式化采集数据方便后续处理 常规的反序列化器如下: public class FlinkDataStreamCDC {public static void main(String[] ar…...

linux基础(2)
目录 一.vi\vim编译器介绍1.三种模式2.vim的使用3.快捷键的使用 二.which,find命令三.grep命令四.wc命令五.管道符六.echo命令1.重定向符 七.tail命令 一.vi\vim编译器介绍 vim\vi是linux中最经典的文本编译器 同图形化界面中的文本编译器是一样的,vi是…...
docker安装zookeeper(单机版)
第一步:拉取镜像 docker pull zookeeper第二步:启动zookeeper docker run -d -e TZ"Asia/Shanghai" -p 2181:2181 -v /home/sunyuhua/docker/zookeeper:/data --name zookeeper --restart always zookeeper...

国际版阿里云/腾讯云免开户:云存储服务:云存储服务能够让你随时随地拜访和同享文件
云存储服务:云存储服务能够让你随时随地拜访和同享文件 云存储服务是一种基于云技术的存储渠道,能够让用户存储、管理和同享各种类型的数据文件,如文档、图片、视频、音频等。这种服务具有许多长处,以下是对其进行的详细分析&…...
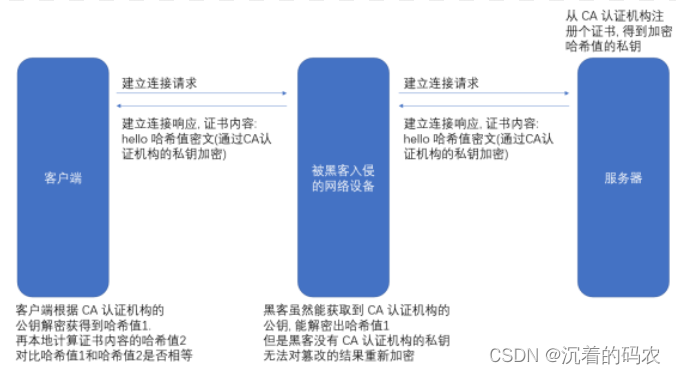
【Java】应用层协议HTTP和HTTPS
HTTP和HTTPS协议 HTTPHTTP协议的工作过程HTTP协议格式抓包工具抓包结果 HTTP请求(Request)URL方法GET方法POST请求其他方法 报头(header)HostContent-lengthContent-TypeUser-AgentRefererCookie 正文(body) HTTP响应HTTP状态码响应报头(header)响应正文(body) 通过form表单构造…...
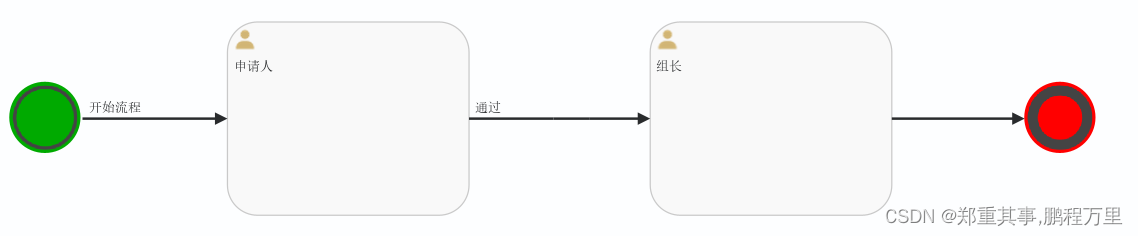
SpringBoot整合Flowable
1. 配置 (1) 引入maven依赖 <dependency><groupId>org.flowable</groupId><artifactId>flowable-spring-boot-starter</artifactId><version>6.7.2</version></dependency><!-- MySQL连接 -->&l…...
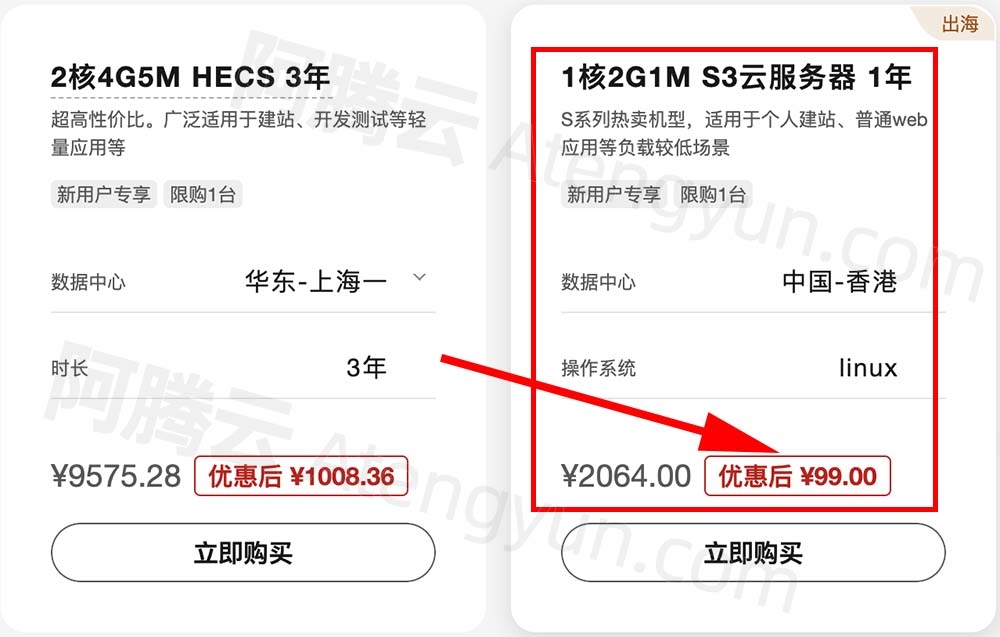
华为云香港S3云服务器性能测评_99元一年租用价格
华为云香港S3云服务器1核2G1M带宽99元一年性能测评,配置为S3云服务器1核2G1M带宽,S系列热卖机型,适用于个人建站、普通web应用等负载较低场景,系统盘为高IO40G系统盘,华为云百科分享华为云香港云服务器配置费用&#x…...

prompt 视频收集
1.ChatGPT Prompt提示词工程 ***** 常用技巧 (基本原则,格式,角色扮演)_哔哩哔哩_bilibili...
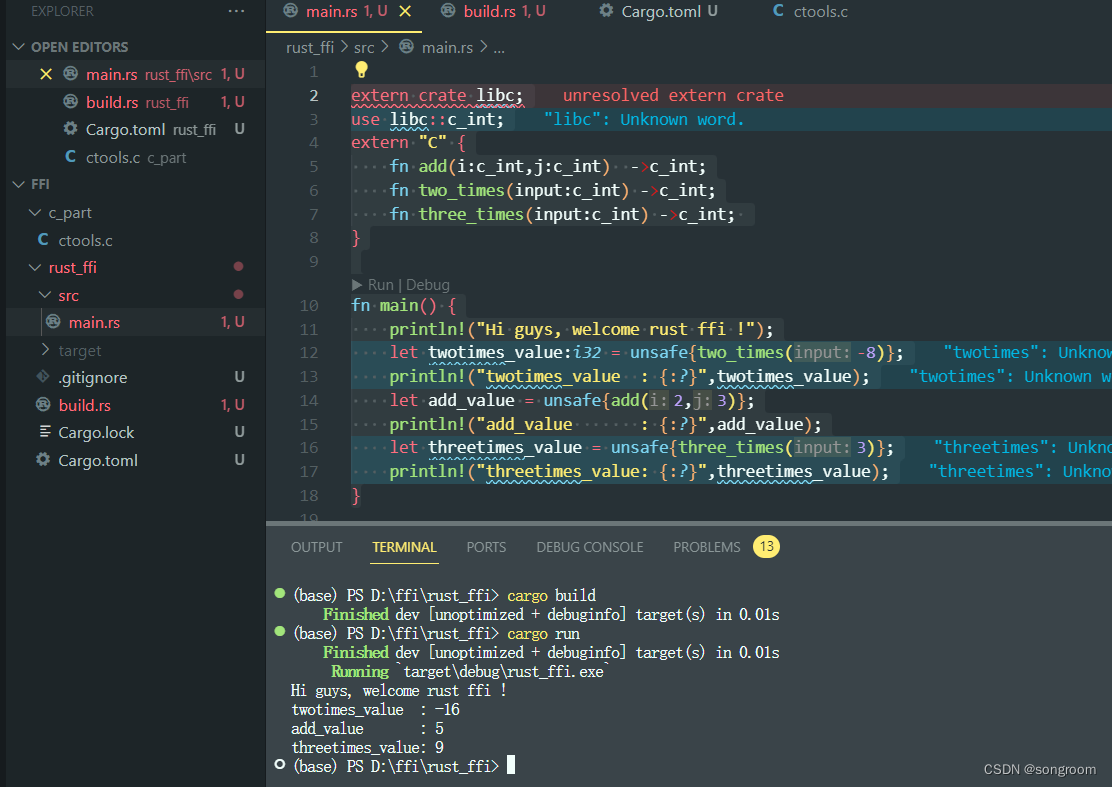
Rust :与C交互
rust调用C端的库函数,有很多方法。今天介绍通过cc库,通过build生成脚本的方式,实现rust调用c端库函数。 1、相关准备: 在ffi目录下,创建了c_part和rust_ffi文件夹。 c_part下放了ctools.c文件,里面有一些…...
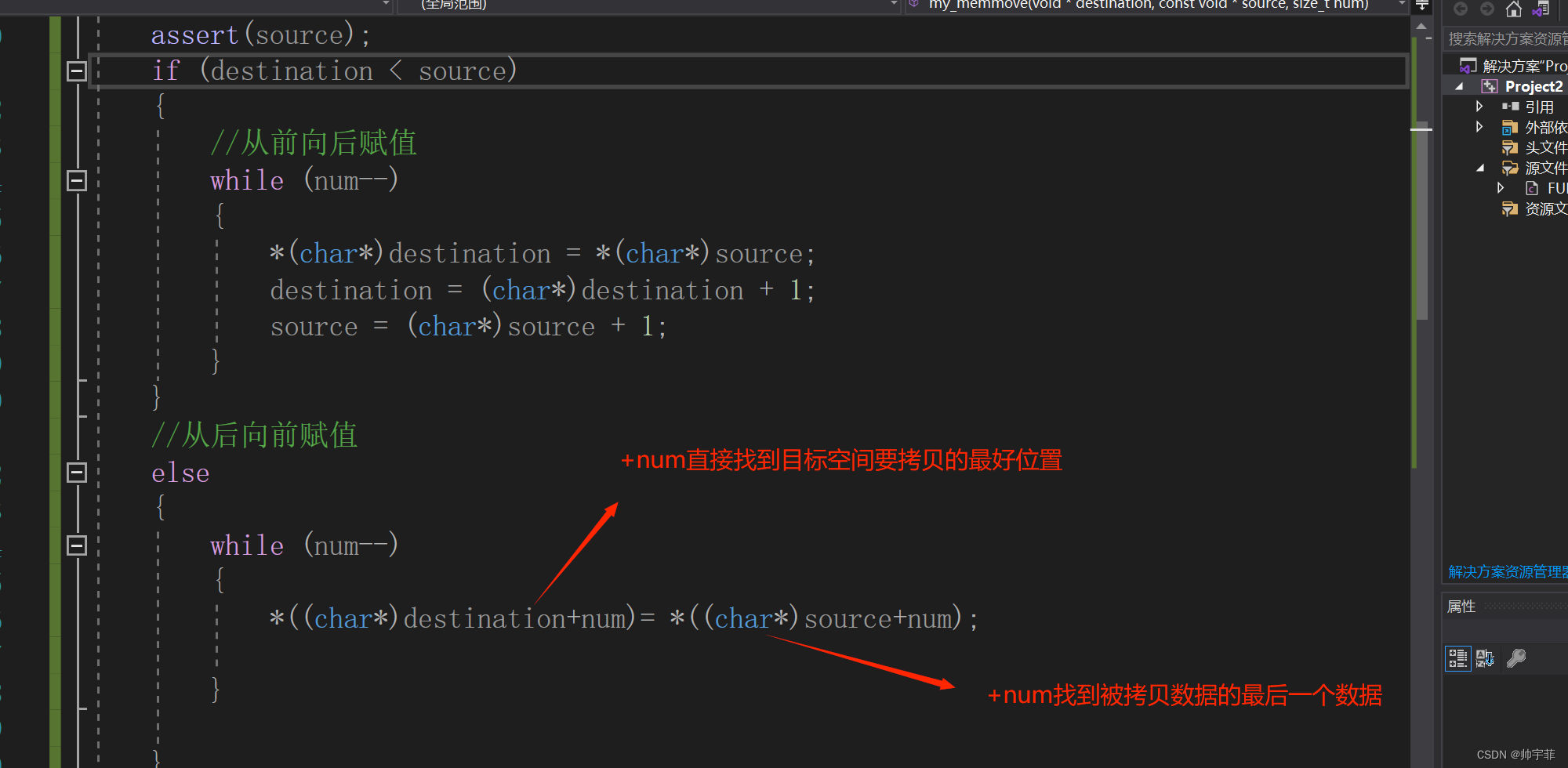
模拟实现C语言--memcpy函数和memmove函数
模拟实现C语言–memcpy函数和memmove函数 文章目录 模拟实现C语言--memcpy函数和memmove函数一、memcpy函数和memmove函数1.1 memcpy函数是什么1.1 memmove函数是什么 二、使用示例2.1 从起始位置复制2.2 从任意位置复制 三、模拟实现3.1 模拟实现1--memcpy函数3.2 针对缺点改进…...

Linux目录
根目录 根目录:“/” 在Linux系统中,根目录指的是整个文件系统的最顶级目录,用符号"/"表示。根目录是文件系统的起点,所有其他目录和文件都嵌套在根目录下面。在根目录下通常会有一些常见的子目录,例如/bin…...
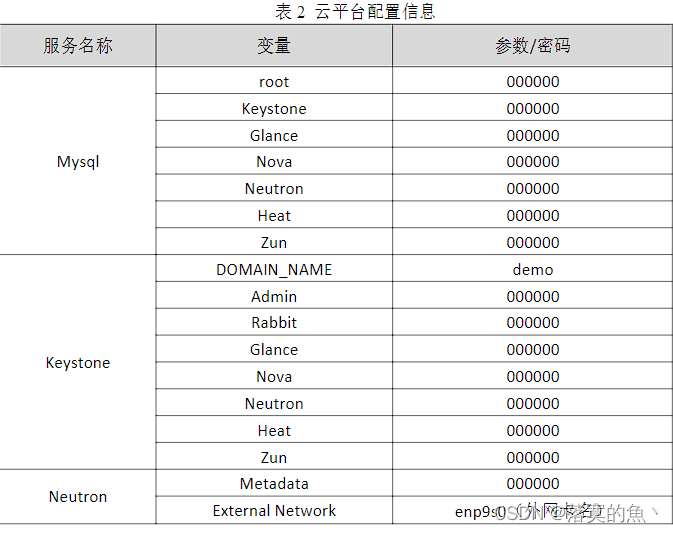
全国职业技能大赛云计算--高职组赛题卷①(私有云)
全国职业技能大赛云计算--高职组赛题卷①(私有云) 第一场次题目:OpenStack平台部署与运维任务1 基础运维任务(5分)任务2 OpenStack搭建任务(15分)任务3 OpenStack云平台运维(15分&am…...

STM32--PWR电源控制
文章目录 PWR电源电源管理器上电复位(POR)和掉电复位(PDR) 可编程电压监测器(PVD)低功耗模式睡眠模式停止模式待机模式 睡眠模式工程停止模式待机模式 PWR STM32的PWR模块是其电源管理系统的核心部分&…...
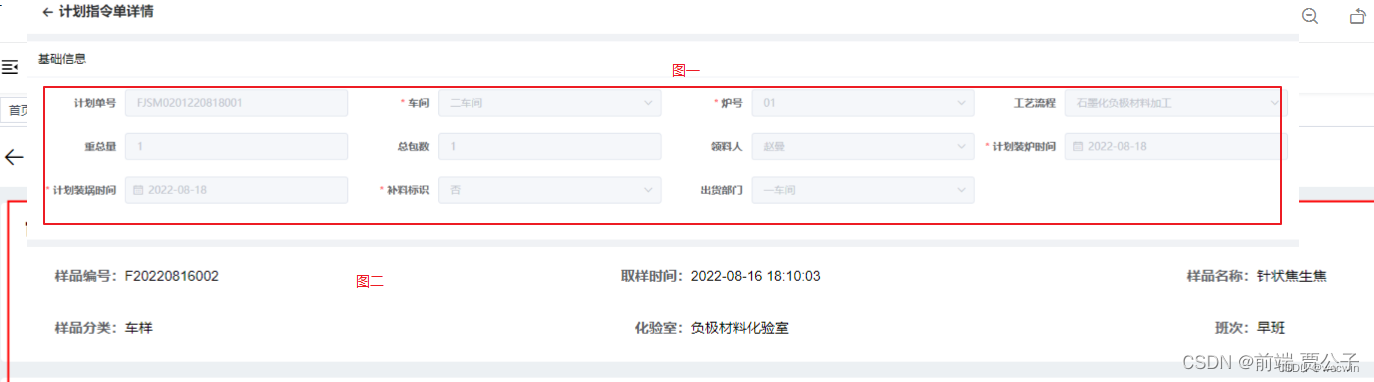
vue+element-ui el-descriptions 详情渲染组件二次封装(Vue项目)
目录 1、需求 2.想要的效果就是由图一变成图二 编辑 3.组件集成了以下功能 4.参数配置 示例代码 参数说明 5,组件 6.页面使用 1、需求 一般后台管理系统,通常页面都有增删改查;而查不外乎就是渲染新增/修改的数据(由输入框变成输…...

Nvme 协议第一章节学习
Nvme Express Base Specification 第一章 简介 1.1概述 NVM ExpressTM(NVMeTM)接口允许主机软件与非易失性存储器子系统通信。 此接口针对企业和客户端固态驱动器进行了优化,通常作为寄存器级接口连接到PCI Express接口。 注:在…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
