元素全排列问题的新思路(DFS,递归,计数器)
目录
前言
1,普通DFS实现1~n的元素全排列
2,计数器+DFS实现重复元素全排列
总结
前言
我们之前看到的全排列问题的解法都是通过交换法达到的,去重的效果也是通过判断当前元素前是否有相同元素来实现,今天我们带来一个全新的思路,使我们直接进行深度优先搜索+一个计数器就可以实现,不用交换。
1,普通DFS实现1~n的元素全排列
我们先一步一步来,先从1~n不重复的开始:
假如说我们现在的n是3,则有以下排列组合:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1仔细观察思考一下,我们列举这些排列组合的时候,是不是我们先固定了一个数字为基准,之后把剩下的数字进行全排列呢?那再继续往下说,我们在把剩下的数字全排列的时候,是不是也会跟前面一样,以一个数字为基准呢?我们推理一下:
第一次:
固定 1 1 ? ? 在2 3里面选固定21 2 ? 在3里面选固定31 2 3 排列出来了以此类推,我们发现这样刚好适合使用递归和回溯算法来实现,我们在排列出来之后跳出递归,之后进行回溯,位数作为我们的参数,理解一下代码:
#include <iostream>using namespace std;int num[11], mark[11], n;void dfs(int p) {if (p == n + 1) {for (int i = 1; i <= n; i++) {cout << num[i] << ' ';}cout << endl;return;}for (int i = 1; i <= n; i++) {if (mark[i] == 0) {num[p] = i;mark[i] = 1;dfs(p + 1);mark[i] = 0;}}
}int main() {cin >> n;dfs(1);return 0;
}这里我们使用一个mark数组来记录这个数字有没有在上一层递归中已经被选择过。
但是当我们输入的是自定义数组且有重复元素的时候,这个方法就失效了。
2,计数器+DFS实现重复元素全排列
我们设想,如果说我们给出一个有重复元素的数组 1 2 2 1,它的重复排列是因为什么?答案是如果以数值为判断标准,他们两个其实并没有区别,如果是交换法,那么以下标为判断标准,第一个2跟第二个2下标虽不同,但是如果与第一个交换,答案还是一样的。所以我们找另一种规律,那就是数量。我们发现这个数组中每种数字的数量是不一样的,这样的话我们每次判断这个数字用没用完就可以了:
void dfs(int p) {if (p == a.size()) { // 位数到了for (int t : a) {cout << t << ' ';}cout << endl;return;}for (int t : num) {if (cot[t] > 0) { // 判断是否要用这个数纯靠计数器a[p] = t;cot[t]--;dfs(p + 1);cot[t]++; // 回溯}}}dfs函数就是这样,当我们使用了一个数字之后,计数器就减去1,回溯时加上1,但是它是怎么完成去重的呢?
这里如果我们直接使用输入时的数据进行递归,那结果是会有重复的,因为在我们回溯的时候,计数器的个数回拨了,但是这个时候循环的元素里又会有一个相同的元素,例如:
1 2 2 dfs时第一次:1 通过 计数器-- 进入递归 1 ? ?
1 不通过 2 通过 计数器-- 进入递归 1 2 ?
1 不同过 2 通过 计数器-- 跳出递归 1 2 2对的我没写错,其实第三个2没用上,因为我们其实只需要数字的种类就可以了,但是继续就会出现重复:
1 2 2 dfs时第一次:最外层递归 ? ? ?
1 通过 计数器-- 进入递归 1 ? ?
1 不通过 2 通过 计数器-- 进入递归 1 2 ?
1 不同过 2 通过 计数器-- 跳出递归 1 2 2回溯1次到了1 ? ?的时候,此时最外层递归还是1,里面的一层第一个 1 和 2已经用掉了,回溯了一次所以计数器的次数还剩一次,此时循环再次到2,不过是第三个2,但是因为回溯过,所以1 2 2再次出现,造成重复。接下来跳出递归后,再回溯了一次,回到了第二层递归,第二层递归循环结束回到了最外层,计数器归到2,最外层开始了2开头.........之后就是一样的剧本
我们通过分析递归了解了是遍历数组时的重复元素造成了结果的重复,而且其实我们依靠计数器的话也不需要这些重复的数据,只要一开始统计一下个数就好。
这样的话我们输入之后把数组过滤一下,1221过滤成12,只记录种类:
// 统计各个数字的个数for (int i = 0; i < a.size(); i++) {cin >> n;cot[n]++;}// 每个数字只添加一个for (int i = 0; i < cot.size(); i++) {if (cot[i] > 0) {num.push_back(i);}}sort(num.begin(), num.end());先排个序可以确保结果也是有序的。
之后我们汇总一下看看整体代码:
//
// Created by 33058 on 2023-09-18.
//
#include <iostream>
#include <vector>
#include <algorithm>using namespace std;vector<int> num, cot(10), a(3);void dfs(int p) {if (p == a.size()) { // 位数到了for (int t : a) {cout << t << ' ';}cout << endl;return;}for (int t : num) {if (cot[t] > 0) { // 判断是否要用这个数纯靠计数器a[p] = t;cot[t]--;dfs(p + 1);cot[t]++; // 回溯}}}int main() {int n;// 统计各个数字的个数for (int i = 0; i < a.size(); i++) {cin >> n;cot[n]++;}// 每个数字只添加一个for (int i = 0; i < cot.size(); i++) {if (cot[i] > 0) {num.push_back(i);}}sort(num.begin(), num.end());dfs(0);return 0;
}
这个是确位数 a 在 1<= a <= 3, 数字n在 0 <= a < 10之间的,开数组的时候10和3可以进行n位的推广。
要注意递归的出口一定是a.size()而不是num.size()因为num只记录了数字的种类,a才是真正的3位数!!
总结
至此全部的内容就结束了,大家可以仔细的理解代码,一步一步剖析递归的过程,从位数少的开始,这样也就好理解了。
相关文章:
)
元素全排列问题的新思路(DFS,递归,计数器)
目录 前言 1,普通DFS实现1~n的元素全排列 2,计数器DFS实现重复元素全排列 总结 前言 我们之前看到的全排列问题的解法都是通过交换法达到的,去重的效果也是通过判断当前元素前是否有相同元素来实现,今天我们带来一个全新的思路…...

机器学习 day35(决策树)
决策树 上图的数据集是一个特征值X采用分类值,即只取几个离散值,同时也是一个二元分类任务,即标签Y只有两个值 上图为之前数据集对应的决策树,最顶层的节点称为根节点,椭圆形节点称为决策节点,矩形节点称…...

小程序引入vant-Weapp保姆级教程及安装过程的问题解决
小知识,大挑战!本文正在参与“程序员必备小知识”创作活动。 本文同时参与 「掘力星计划」,赢取创作大礼包,挑战创作激励金 当你想在小程序里引入vant时,第一步:打开官方文档,第二步ÿ…...

LeetCode 周赛上分之旅 #45 精妙的 O(lgn) 扫描算法与树上 DP 问题
⭐️ 本文已收录到 AndroidFamily,技术和职场问题,请关注公众号 [彭旭锐] 和 BaguTree Pro 知识星球提问。 学习数据结构与算法的关键在于掌握问题背后的算法思维框架,你的思考越抽象,它能覆盖的问题域就越广,理解难度…...

JavaScript-DOM实战案例
一、window定时器 1.window定时器方法 有时我们并不想立即执行一个函数,而是等待特定一段时间之后再执行,我们称之为“计划调用(scheduling a call)”。 目前有两种方式可以实现: setTimeout 允许我们将函数推迟到一…...
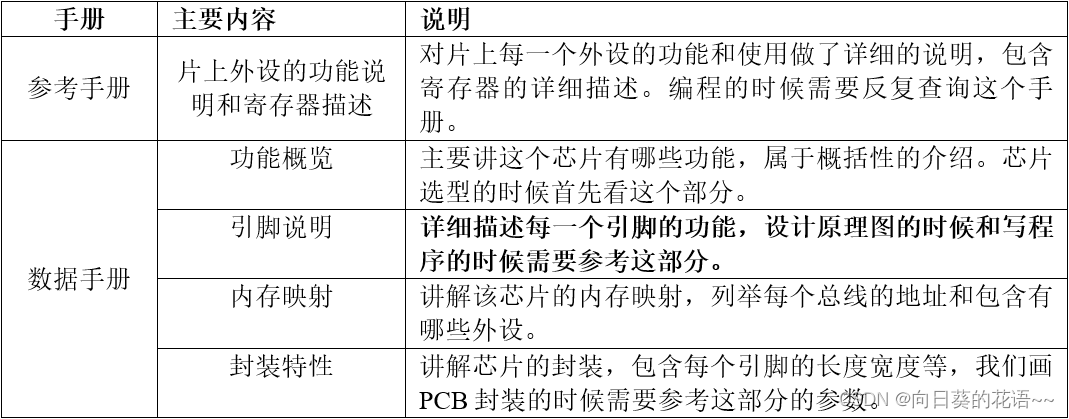
STM32 学习笔记1:STM32简介
1 概述 STM32,从字面上来理解,ST 是意法半导体,M 是 Microelectronics 的缩写,32 表示 32 位,合起来理解,STM32 就是 ST 公司开发的 32 位微控制器。是一款基于 ARM 公司推出的基于 ARMv7 架构的 32 位 Co…...

Hadoop-Hbase
1. Hbase安装 1.1 安装zookeeper、 hbase 解压至/opt/soft,并分别改名 配置环境变量并source生效 #ZK export ZOOKEEPER_HOME/opt/soft/zk345 export PATH$ZOOKEEPER_HOME/bin:$PATH #HBASE_HOME export HBASE_HOME/opt/soft/hbase235 export PATH$HBASE_HOME/b…...

关于不停机发布新版本程序的方式
“不停机发布新版本程序”,暂且这么称呼吧,其实就是所说的滚动发布、灰度发布、金丝雀发布和蓝绿发布。 之所以会总结性地提一下这几个概念,主要是本次出门游历,流浪到了乌兰察布市四王子旗,在这儿遇上了个有趣儿的家伙…...
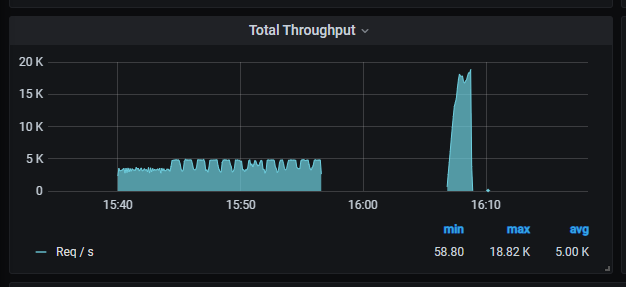
MeterSphere压测,出现HttpHostConnectException
现象:MeterSphere更换压力机后,压测出现出现HttpHostConnectException 解决方案: net.ipv4.tcp_tw_reuse默认是0或者2,更改为1 net.ipv4.tcp_tw_reuse,表示是否允许重新应用处于TIME-WAIT状态的socket用于新的TCP连…...

cherry-pick
要将dev分支的某次提交给master分支,可以使用以下命令: 1. 切换到dev分支:git checkout dev 2. 查看提交历史,找到要提交给master的某次提交的commit hash(假设为 <commit_hash>) 3. 切换到master…...
opencv形状目标检测
1.圆形检测 OpenCV图像处理中“找圆技术”的使用-图像处理-双翌视觉OpenCV图像处理中“找圆技术”的使用,图像处理,双翌视觉https://www.shuangyi-tech.com/news_224.htmlopencv 找圆心得,模板匹配比霍夫圆心好用 - 知乎1 相比较霍夫找直线算法, 霍夫找…...

k8s中无法获取到nginx-ingress的客户端真实ip地址x-forwarded-for
1.查看阿里云的nginx-ingress配置文档https://help.aliyun.com/document_detail/42205.html 容器K8s配置方案 如果您的服务部署在K8s上,K8s会将真实的客户端IP记录在X-Original-Forwarded-For字段中,并将WAF回源地址记录在X-Forwarded-For字段中。您需要…...
索引实践(2))
MySQL(4)索引实践(2)
一、分页优化 limit 1000 10, 其实不是只查询出10条记录,mysql底层会查询出1100条,然后舍去前1000条 所以,随着页的增多,查询效率会降低 1、可以使用取范围的方式比如id>1000 方式优化 2、使用关联查询优化…...

Kafka【命令行操作】
Kafka 命令行操作 Kafka 主要包括三大部分:生产者、主题分区节点、消费者。 1、Topic 命令行操作 也就是我们 kafka 下的脚本 kafka-topics.sh 的相关操作。 常用命令行操作 参数 描述 --bootstrap-server <String: server toconnect to> 连接的Kafka …...
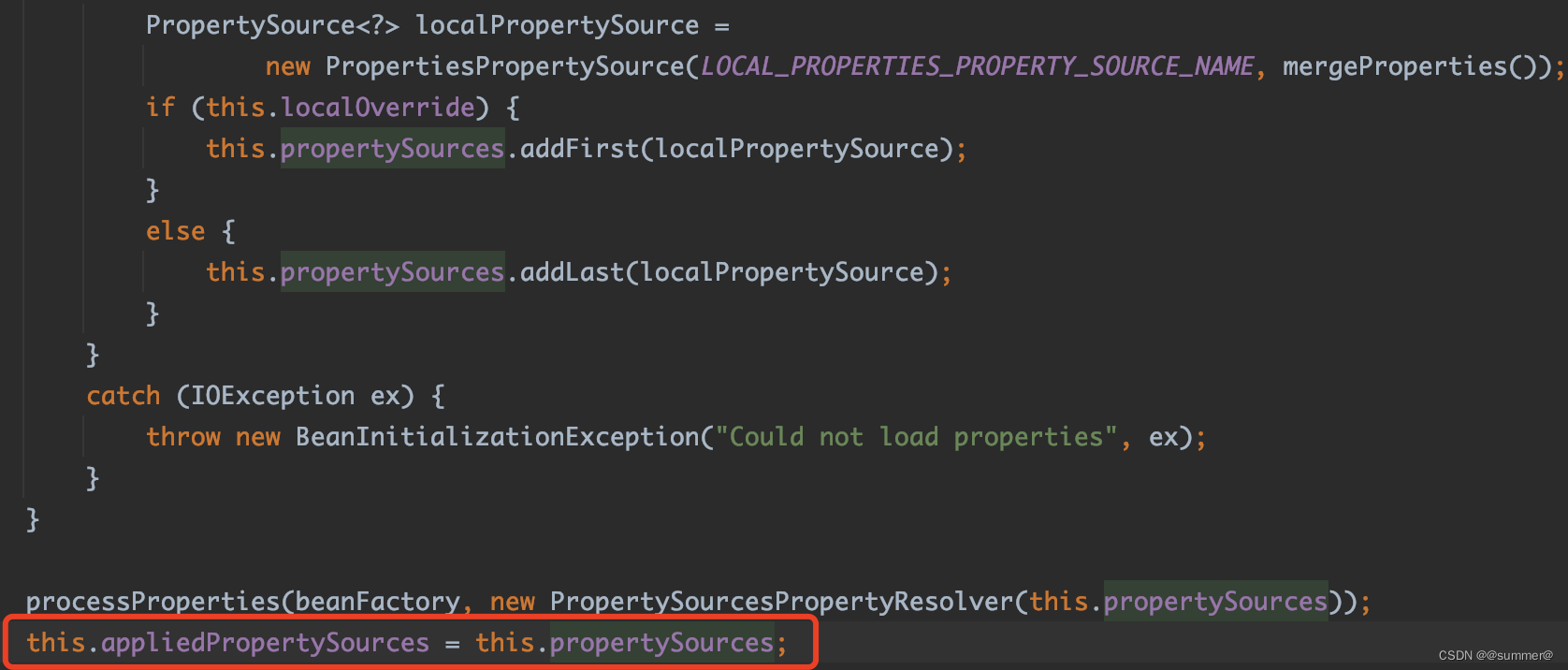
springboot配置注入增强(二)属性注入的原理
一 原理 1 配置的存储 springboot在启动的时候会后构建一个org.springframework.core.env.Environment类型的对象,这个对象就是用于存储配置,如图springboot会在启动的最开始创建一个Environment对象 这个webApplicationType的枚举是在new SpringAppli…...

Android 使用Camera1实现相机预览、拍照、录像
1. 前言 本文介绍如何从零开始,在Android中实现Camera1的接入,并在文末提供Camera1Manager工具类,可以用于快速接入Camera1。 Android Camera1 API虽然已经被Google废弃,但有些场景下不得不使用。 并且Camera1返回的帧数据是NV21…...
)
2024字节跳动校招面试真题汇总及其解答(四)
12.Java的类加载机制 Java的类加载机制是指将描述类的数据从Class文件加载到内存,并对数据进行校验、转换解析和初始化,最终形成可以被虚拟机直接使用的Java类型,这个过程被称作虚拟机的类加载机制。 类的加载过程分为以下五个阶段: 加载:将Class文件从磁盘读入内存,并…...
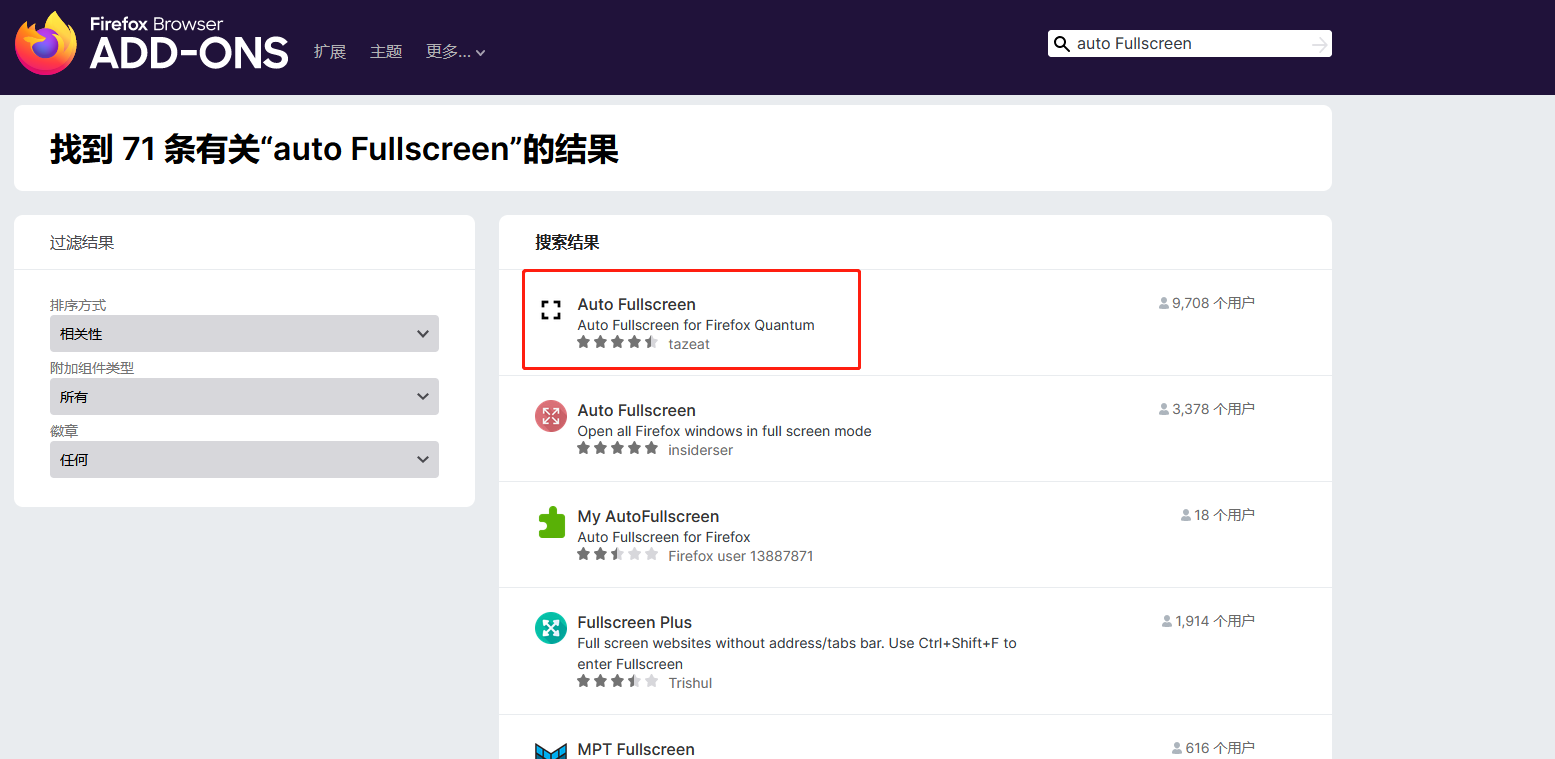
网页的快捷方式打开自动全屏--Chrome、Firefox 浏览器相关设置
Firefox 的全屏方式与 Chrome 不同,Chrome 自带全屏模式以及APP模式,通过简单的参数即可设置,而Firefox暂时么有这个功能,Firefox 的全屏功能可以通过全屏插件实现。 全屏模式下,按 F11 不会退出全屏,鼠标…...
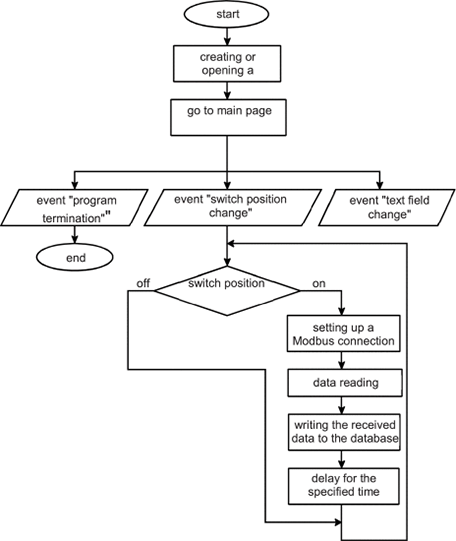
LabVIEW使用ModbusTCP协议构建分布式测量系统
LabVIEW使用ModbusTCP协议构建分布式测量系统 分布式测量系统主要用于监控远程物体。这种系统允许对系统用户获得的数据进行全面的数据收集、处理、存储和组织访问。它们可能包括许多不同类型的传感器。 在任何具有互联网接入的个人计算机上运行的软件都会发送来自传感器的测…...
unity学习第1天
本身也具有一些unity知识,包括Eidtor界面使用、Shader效果实现、性能分析,但对C#、游戏逻辑不太清楚,这次想从开发者角度理解游戏,提高C#编程,从简单的unity游戏理解游戏逻辑,更好的为工作服务。 unity201…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...
