最小二乘法
Least Square Method
- 1、相关的矩阵公式
- 2、线性回归
- 3、最小二乘法
- 3.1、损失函数(Loss Function)
- 3.2、多维空间的损失函数
- 3.3、解析法求解
- 3.4、梯度下降法求解
1、相关的矩阵公式
P r e c o n d i t i o n : ξ ∈ R n , A ∈ R n ∗ n i : σ A ξ σ ξ = A T i i : σ ξ T A ξ σ ξ = A T ξ + A ξ i i i : ( A B ) T = B T A T i v : ( A + B ) T = A T + B T v : ∥ ξ ∥ = ξ T ξ \begin{array}{l} Precondit{\rm{i}}on:\xi \in {R^n},A \in {R^{n*n}}\\ \\ i:\frac{{\sigma A\xi }}{{\sigma \xi }} = {A^T}\\ \\ ii:\frac{{\sigma {\xi ^T}A\xi }}{{\sigma \xi }} = {A^T}\xi + A\xi \\ \\ iii:{\left( {AB} \right)^T} = {B^T}{A^T}\\ \\ iv:{\left( {A + B} \right)^T} = {A^T} + {B^T}\\ \\ v:\left\| \xi \right\| = {\xi ^T}\xi \end{array} Precondition:ξ∈Rn,A∈Rn∗ni:σξσAξ=ATii:σξσξTAξ=ATξ+Aξiii:(AB)T=BTATiv:(A+B)T=AT+BTv:∥ξ∥=ξTξ
2、线性回归
线性回归(Linear Regression)个人理解大概是说,一组数据基本上服从线性分布。举一个在二维平面中线性回归的例子,如下图所示,我们可以找到一条表达式为 y = a x + b y=ax+b y=ax+b的直线来大概的拟合这些数据。进而,我们可以用这条直线去预测新输入的点的相应的坐标。那么这种寻找线性方程去拟合数据的方式我们称之为线性回归。

3、最小二乘法
3.1、损失函数(Loss Function)
在二维平面中,我们可以设这条可以拟合大多数数据的直线的表达式如下:
h ( θ ) = θ 1 x + θ 2 h\left( \theta \right) = {\theta _1}{x} + {\theta _2} h(θ)=θ1x+θ2
其中 θ 1 {{\theta _1}} θ1和 θ 2 {{\theta _2}} θ2就是 y = a x + b y = ax + b y=ax+b中的 a a a和 b b b,只是换了一种表达而已。
接着,可以求得平面上每一个点在这条直线上对应的坐标(即估计值):
h 1 ( θ ) = θ 1 x 1 + θ 2 h 2 ( θ ) = θ 1 x 2 + θ 2 . . . . h n ( θ ) = θ 1 x n + θ 2 \begin{array}{l} {h_1}\left( \theta \right) = {\theta _1}{x_1} + {\theta _2}\\ {h_2}\left( \theta \right) = {\theta _1}{x_2} + {\theta _2}\\ ....\\ {h_n}\left( \theta \right) = {\theta _1}{x_n} + {\theta _2} \end{array} h1(θ)=θ1x1+θ2h2(θ)=θ1x2+θ2....hn(θ)=θ1xn+θ2
再求这些点在直线上的坐标和真实坐标的差的平方,就得到损失函数的表达式。
L ( θ ) = ∑ i = 1 m ( h i ( θ ) − f ( x i ) ) 2 L\left( \theta \right) = \sum\limits_{i = 1}^m {{{\left( {{h_i}\left( \theta \right) - f\left( {{x_i}} \right)} \right)}^2}} L(θ)=i=1∑m(hi(θ)−f(xi))2
其中 f ( x i ) {f\left( {{x_i}} \right)} f(xi)则是 x i {{x_i}} xi对应的真实坐标值。
因此,可以通过损失函数 L ( θ ) L\left( \theta \right) L(θ)来找出适当的 θ 1 {{\theta _1}} θ1和 θ 2 {{\theta _2}} θ2,使其 f ( x i ) {f\left( {{x_i}} \right)} f(xi)之间的方差最小。求解方法放在后面讲。
3.2、多维空间的损失函数
在 m m m维线性空间中,有 n n n个点。其对应的预测方程应该如下:
h 1 ( θ ) = θ 1 x 11 + θ 2 x 12 + . . . + θ m − 1 x 1 m − 1 + θ m h 2 ( θ ) = θ 1 x 21 + θ 2 x 22 + . . . + θ m − 1 x 2 m − 1 + θ m . . . h n ( θ ) = θ 1 x n 1 + θ 2 x n 2 + . . . + θ m − 1 x n m − 1 + θ m \begin{array}{l} {h_1}\left( \theta \right) = {\theta _1}{x_{11}} + {\theta _2}{x_{12}} + ... + {\theta _{m - 1}}{x_{1m - 1}} + {\theta _m}\\ {h_2}\left( \theta \right) = {\theta _1}{x_{21}} + {\theta _2}{x_{22}} + ... + {\theta _{m - 1}}{x_{2m - 1}} + {\theta _m}\\ ...\\ {h_n}\left( \theta \right) = {\theta _1}{x_{n1}} + {\theta _2}{x_{n2}} + ... + {\theta _{m - 1}}{x_{nm - 1}} + {\theta _m} \end{array} h1(θ)=θ1x11+θ2x12+...+θm−1x1m−1+θmh2(θ)=θ1x21+θ2x22+...+θm−1x2m−1+θm...hn(θ)=θ1xn1+θ2xn2+...+θm−1xnm−1+θm
其中 n > m n>m n>m(方程数量等比未知数多才能有解)。损失函数的表达式依旧如此:
L ( θ ) = ∑ i = 1 m ( h i ( θ ) − f ( x i ) ) 2 L\left( \theta \right) = \sum\limits_{i = 1}^m {{{\left( {{h_i}\left( \theta \right) - f\left( {{x_i}} \right)} \right)}^2}} L(θ)=i=1∑m(hi(θ)−f(xi))2
那么再将以上的所有变量矩阵化:

可以得到损失函数的表达式为:
L ( θ ) = ∥ X θ − F ∥ 2 = ( X θ − F ) T ( X θ − F ) L\left( \theta \right) = {\left\| {X\theta - F} \right\|^2} = {\left( {X\theta - F} \right)^T}\left( {X\theta - F} \right) L(θ)=∥Xθ−F∥2=(Xθ−F)T(Xθ−F)
再展开化简:
L ( θ ) = ∥ X θ − F ∥ 2 = ( X θ − F ) T ( X θ − F ) = ( θ T X T − F T ) ( X θ − F ) = θ T X T X θ − θ T X T F − F T X θ + F T F = θ T X T X θ − 2 F T X θ + F T F \begin{array}{l} L\left( \theta \right) = {\left\| {X\theta - F} \right\|^2} = {\left( {X\theta - F} \right)^T}\left( {X\theta - F} \right)\\ \\ = \left( {{\theta ^T}{X^T} - {F^T}} \right)\left( {X\theta - F} \right) = {\theta ^T}{X^T}X\theta - {\theta ^T}{X^T}F - {F^T}X\theta + {F^T}F\\ \\ = {\theta ^T}{X^T}X\theta - 2{F^T}X\theta + {F^T}F \end{array} L(θ)=∥Xθ−F∥2=(Xθ−F)T(Xθ−F)=(θTXT−FT)(Xθ−F)=θTXTXθ−θTXTF−FTXθ+FTF=θTXTXθ−2FTXθ+FTF
根据上文,我们知道化简的目的是为了找到适当的 θ \theta θ使得损失函数 L ( θ ) L\left( \theta \right) L(θ)最小,而常用的求 θ \theta θ有两种,分别是解析法求解和梯度下降法。
3.3、解析法求解
从高数可以知,当偏导等于零时,该点是极值点(说的不严谨emm)。所以我们直接求偏导,另其为零即可得 θ \theta θ。
σ L ( θ ) σ θ = 2 X T X θ − 2 X T F = 0 θ = ( X T X ) − 1 X T F \begin{array}{l} \frac{{\sigma L\left( \theta \right)}}{{\sigma \theta }} = 2{X^T}X\theta - 2{X^T}F = 0\\ \\ \theta = {\left( {{X^T}X} \right)^{ - 1}}{X^T}F \end{array} σθσL(θ)=2XTXθ−2XTF=0θ=(XTX)−1XTF
但这种方法要求 X T X {{{X^T}X}} XTX是可逆的,即行列式不为零or满秩。很多时候这个条件并不成立,所以在机器学习(Machine Learning)中经常用到梯度下降法。
3.4、梯度下降法求解
梯度下降基本思想是先随便取一个 θ i {\theta _i} θi,然后带入下式看看损失函数多大,然后再在 θ i {\theta _i} θi基础上,取一个稍微小一点或大一点的 θ j {\theta _j} θj带入下式,看看此时的损失函数多大。如此往复,找到那个最优的 θ \theta θ的取值。
L ( θ i ) = θ i T X T X θ i − 2 F T X θ i + F T F L\left( {{\theta _{\rm{i}}}} \right) = {\theta _i}^T{X^T}X{\theta _i} - 2{F^T}X{\theta _i} + {F^T}F L(θi)=θiTXTXθi−2FTXθi+FTF
相关文章:

最小二乘法
Least Square Method 1、相关的矩阵公式2、线性回归3、最小二乘法3.1、损失函数(Loss Function)3.2、多维空间的损失函数3.3、解析法求解3.4、梯度下降法求解 1、相关的矩阵公式 P r e c o n d i t i o n : ξ ∈ R n , A ∈ R n ∗ n i : σ A ξ σ ξ…...

使用stelnet进行安全的远程管理
1. telnet有哪些不足? 2.ssh如何保证数据传输安全? 需求:远程telnet管理设备 用户定义需要在AAA模式下: 开启远程登录的服务:定义vty接口 然后从R2登录:是可以登录的 同理R3登录: 在R1也可以查…...

python 二手车数据分析以及价格预测
二手车交易信息爬取、数据分析以及交易价格预测 引言一、数据爬取1.1 解析数据1.2 编写代码爬1.2.1 获取详细信息1.2.2 数据处理 二、数据分析2.1 统计分析2.2 可视化分析 三、价格预测3.1 价格趋势分析(特征分析)3.2 价格预测 引言 本文着眼于车辆信息,结合当下较…...
JAVA医药进销存管理系统(附源码+调试)
JAVA医药进销存管理系统 功能描述 (1)登录模块:登录信息等存储在数据库中 (2)基本信息模块:分为药品信息模块、客户情况模块、供应商情况模块; (3)业务管理模块&#x…...

H5 <blockquote> 标签
主要应用于:内容引用 标签定义及使用说明 <blockquote> 标签定义摘自另一个源的块引用。 浏览器通常会对 <blockquote> 元素进行缩进。 提示和注释 提示:如果标记是不需要段落分隔的短引用,请使用 <q>。 HTML 4.01 与 H…...
nginx配置指南
nginx.conf配置 找到Nginx的安装目录下的nginx.conf文件,该文件负责Nginx的基础功能配置。 配置文件概述 Nginx的主配置文件(conf/nginx.conf)按以下结构组织: 配置块功能描述全局块与Nginx运行相关的全局设置events块与网络连接有关的设置http块代理…...

【数据结构】优先级队列(堆)
文章目录 💐1. 优先级队列1.1 概念 💐2.堆的概念及存储方式2.1 什么是堆2.2 为什么要用完全二叉树描述堆呢?2.3 为什么说堆是在完全二叉树的基础上进行的调整?2.4 使用数组还原完全二叉树 💐3. 堆的常用操作-模拟实现3…...
前端笔试2
1.下面哪一个是检验对象是否有一个以自身定义的属性? foo.hasOwnProperty("bar")bar in foo foo["bar"] ! undefinedfoo.bar ! null 解析: bar in foo 检查 foo 对象是否包含名为 bar 的属性,但是这个属性可以是从原型链继承来的&a…...

LeetCode:66.加一
66.加一 来源:力扣(LeetCode) 链接: https://leetcode.cn/problems/plus-one/description/ 给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。 最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。 你可以假设除了整数 0 之外,这个整数…...

Redis 常用命令
目录 全局命令 1)keys 2)exists 3) del(delete) 4)expire 5)type SET命令 GET命令 MSET 和 MGET命令 其他SET命令 计数命令 redis-cli,进入redis 最核心的命令:我们这里只是先介绍 set 和 get 最简单的操作…...
用于字符和字符串的区别)
Integer.valueOf()用于字符和字符串的区别
LeetCode 17 电话号码的字母组合 先贴代码 class Solution {List<String> result new ArrayList<>();String temp new String("");Integer num;public List<String> letterCombinations(String digits) {dfs(digits, 0);return result;} publi…...
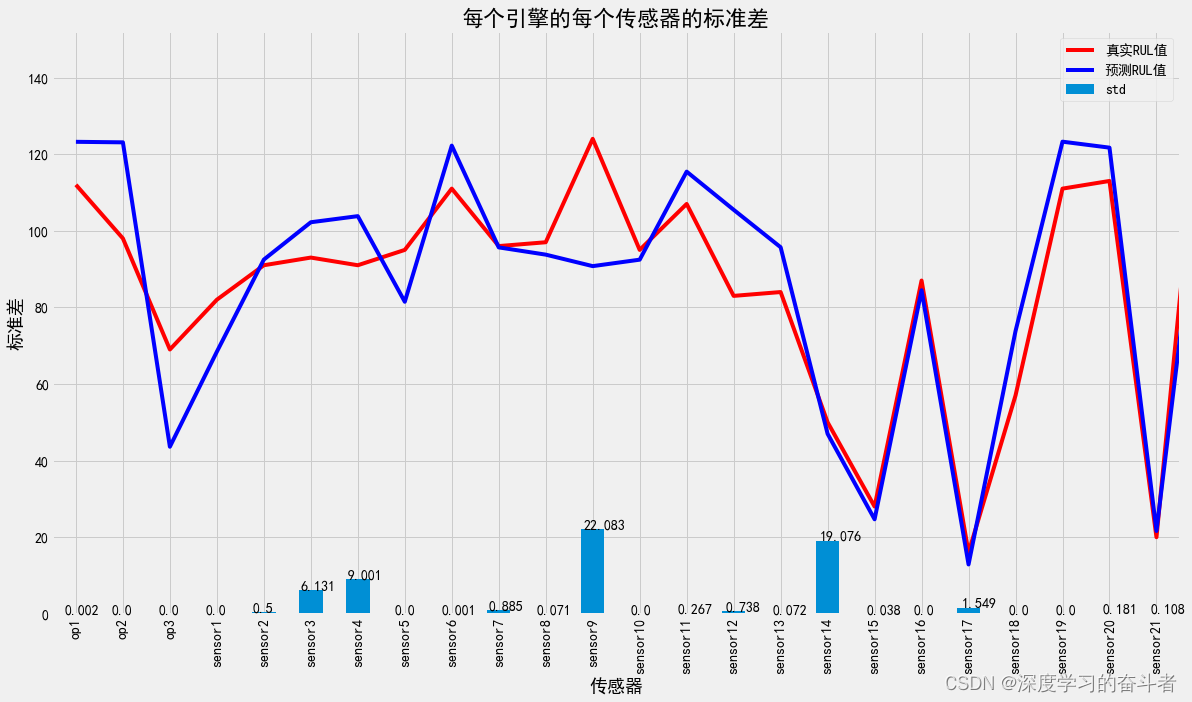
机械寿命预测(基于NASA C-MAPSS数据的剩余使用寿命RUL预测,Python代码,CNN_LSTM模型,有详细中文注释)
1.效果视频:机械寿命预测(NASA涡轮风扇发动机剩余使用寿命RUL预测,Python代码,CNN_LSTM模型,有详细中文注释)_哔哩哔哩_bilibili 环境库版本: 2.数据来源:https://www.nasa.gov/int…...
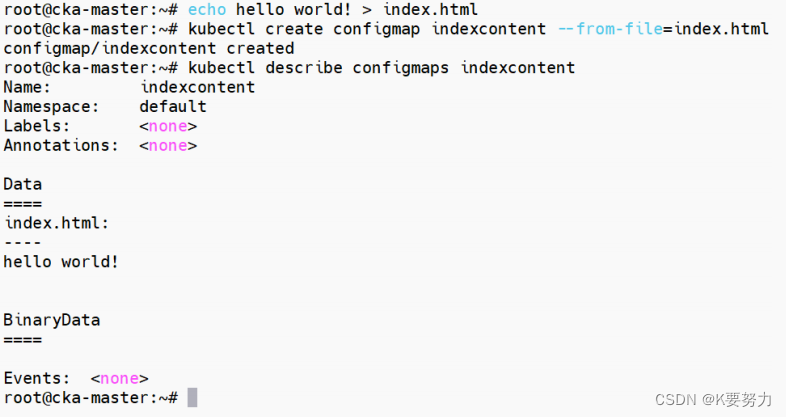
ConfigMaps-1
文章目录 主要内容一.使用 YAML 文件创建1.在data节点创建了一些键值:代码如下(示例): 2.解释 二.使用命令行创建1.创建了一个名为 person 的键值:代码如下(示例): 2.解释3.创建了一个 index.html 文件&…...

docker上安装es
安装docker 1 安装docker依赖 yum install -y yum-utils2 设置docker仓库镜像地址 yum-config-manager --add-repo http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo3 安装制定版本的docker yum -y install docker-ce-20.10.17-3.el74 查看是否安装成功 y…...
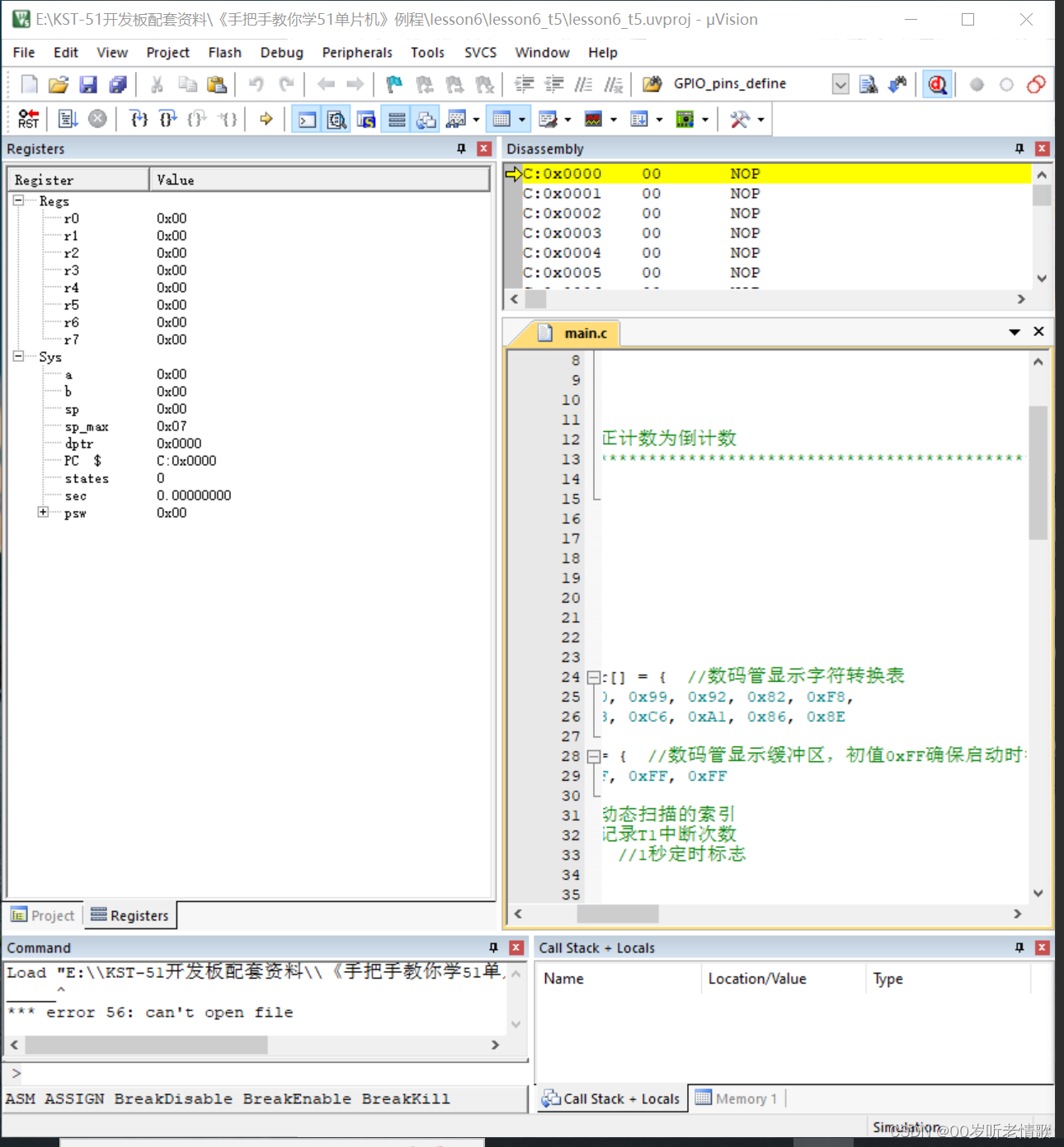
#循循渐进学51单片机#c语言基础和流水灯实现#not.3
1、熟练掌握二进制、十进制和十六进制的转换方法。 多少进制就是多少之间相加,比如十六进制就是十六一次一加;二进制转化十六进制,分成四个一组。 2、C语言变量类型与取值范围,for、while等基本语句的用法。 for、while等基本语句…...
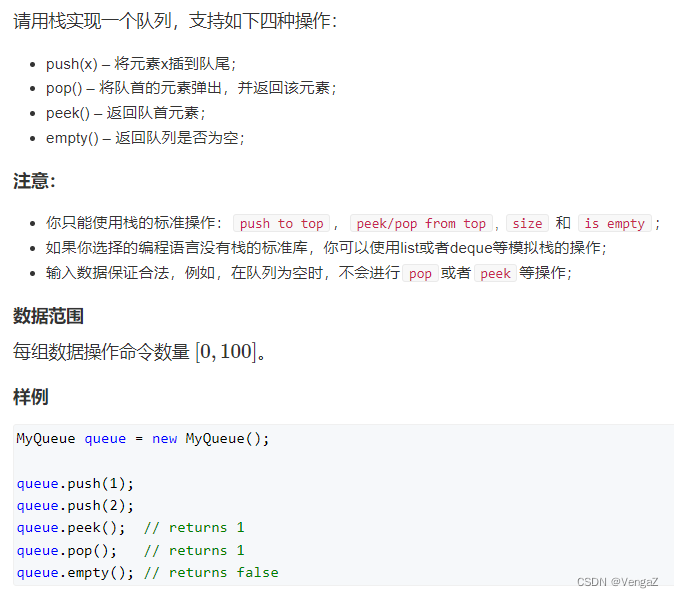
算法刷题 week3
这里写目录标题 1.重建二叉树题目题解(递归) O(n) 2.二叉树的下一个节点题目题解(模拟) O(h) 3.用两个栈实现队列题目题解(栈,队列) O(n) 1.重建二叉树 题目 题解 (递归) O(n) 递归建立整棵二叉树:先递归创建左右子树,然后创建根节点&…...
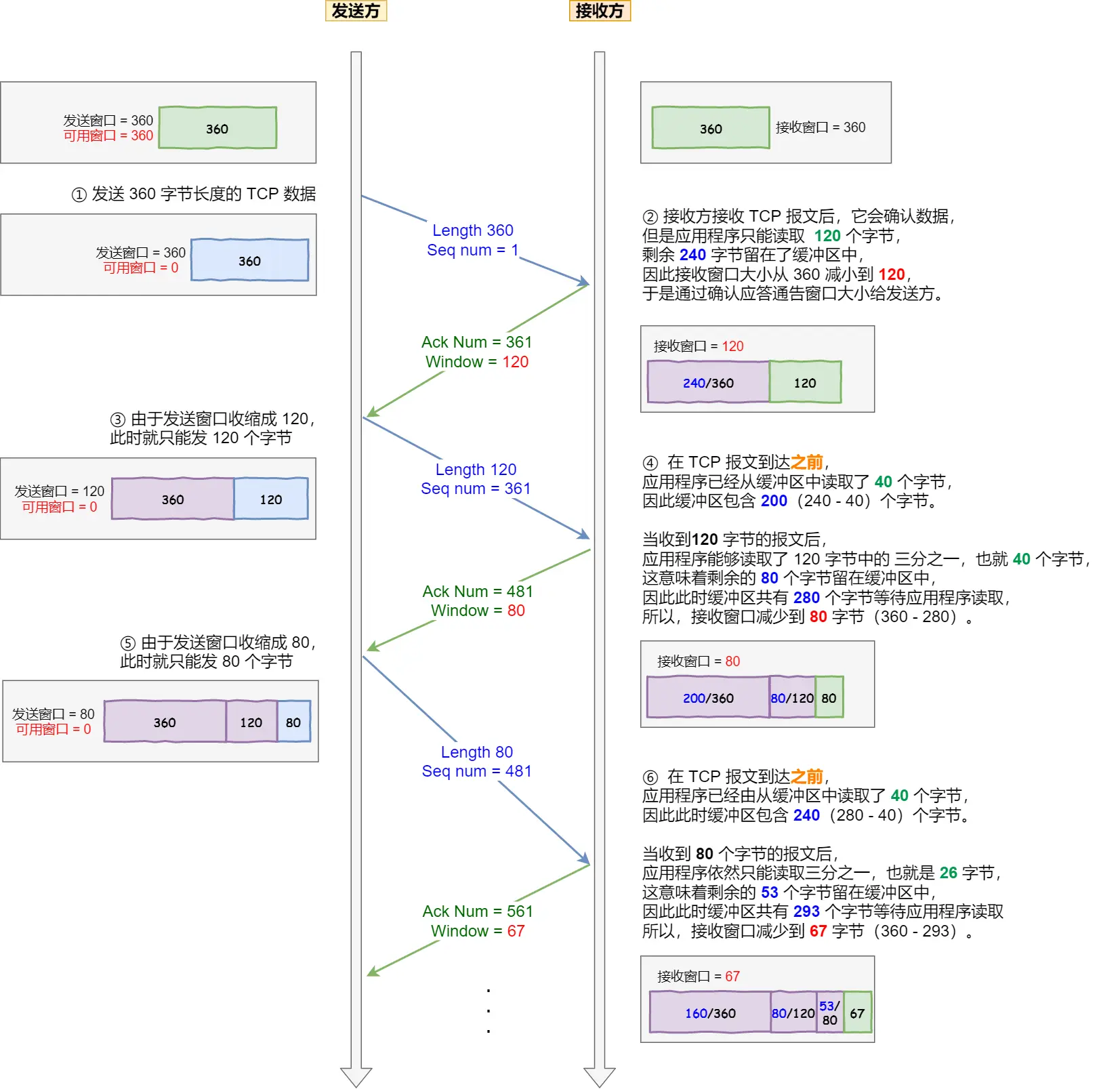
TCP详解之流量控制
TCP详解之流量控制 发送方不能无脑的发数据给接收方,要考虑接收方处理能力。 如果一直无脑的发数据给对方,但对方处理不过来,那么就会导致触发重发机制,从而导致网络流量的无端的浪费。 为了解决这种现象发生,TCP 提…...

mac根目录下创建文件不能问题
mac根目录下创建文件不能问题 解决办法2: 原因 mac os引入了系统完整性保护(SIP)机制,无法在/、/usr目录下新建文件 解决办法1: 打开终端,输入 csrutil status显示enabled表示启用了SIP,接下来需要禁用SIP…...

stable diffusion model训练遇到的问题【No module named ‘triton‘】
一天早晨过来,发现昨天还能跑的diffusion代码,突然出现了【No module named ‘triton’】的问题,导致本就不富裕的显存和优化速度雪上加霜,因此好好探究了解决方案。 首先是原因,由于早晨过来发现【电脑重启】导致了【…...

线性dp,优化记录,273. 分级
273. 分级 273. 分级 - AcWing题库 给定长度为 N 的序列 A,构造一个长度为 N 的序列 B,满足: B 非严格单调,即 B1≤B2≤…≤BN 或 B1≥B2≥…≥BN。最小化 S∑Ni1|Ai−Bi|。 只需要求出这个最小值 S。 输入格式 第一行包含一…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...
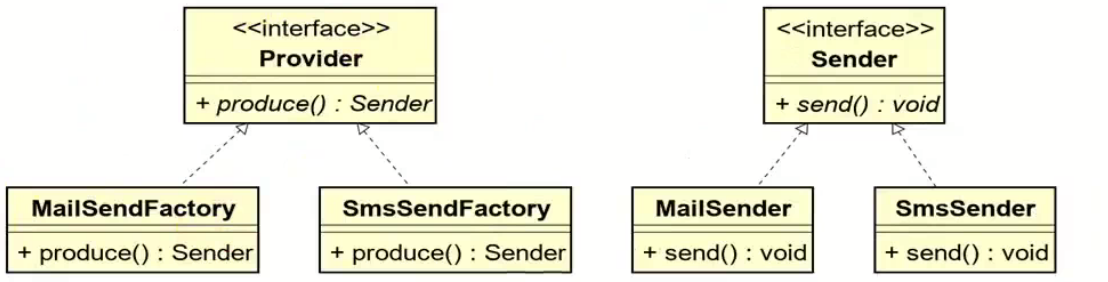
工厂方法模式和抽象工厂方法模式的battle
1.案例直接上手 在这个案例里面,我们会实现这个普通的工厂方法,并且对比这个普通工厂方法和我们直接创建对象的差别在哪里,为什么需要一个工厂: 下面的这个是我们的这个案例里面涉及到的接口和对应的实现类: 两个发…...
