java leetcodetop100 (3,4 )最长连续数列,移动零
top3 最长连续数列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。 * * 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 * * * * 示例 1: * * 输入:nums = [100,4,200,1,3,2] * 输出:4 解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
我们考虑枚举数组中的每个数 xxx,考虑以其为起点,不断尝试匹配 x+1,x+2,⋯x+1, x+2, \cdotsx+1,x+2,⋯ 是否存在,假设最长匹配到了 x+yx+yx+y,那么以 xxx 为起点的最长连续序列即为 x,x+1,x+2,⋯ ,x+yx, x+1, x+2, \cdots, x+yx,x+1,x+2,⋯,x+y,其长度为 y+1y+1y+1,我们不断枚举并更新答案即可。
对于匹配的过程,暴力的方法是 O(n)O(n)O(n) 遍历数组去看是否存在这个数,但其实更高效的方法是用一个哈希表存储数组中的数,这样查看一个数是否存在即能优化至 O(1)O(1)O(1) 的时间复杂度。
仅仅是这样我们的算法时间复杂度最坏情况下还是会达到 O(n2)O(n^2)O(n
2
)(即外层需要枚举 O(n)O(n)O(n) 个数,内层需要暴力匹配 O(n)O(n)O(n) 次),无法满足题目的要求。但仔细分析这个过程,我们会发现其中执行了很多不必要的枚举,如果已知有一个 x,x+1,x+2,⋯ ,x+yx, x+1, x+2, \cdots, x+yx,x+1,x+2,⋯,x+y 的连续序列,而我们却重新从 x+1x+1x+1,x+2x+2x+2 或者是 x+yx+yx+y 处开始尝试匹配,那么得到的结果肯定不会优于枚举 xxx 为起点的答案,因此我们在外层循环的时候碰到这种情况跳过即可。
那么怎么判断是否跳过呢?由于我们要枚举的数 xxx 一定是在数组中不存在前驱数 x−1x-1x−1 的,不然按照上面的分析我们会从 x−1x-1x−1 开始尝试匹配,因此我们每次在哈希表中检查是否存在 x−1x-1x−1 即能判断是否需要跳过了。
通过hash表来实现
public class Top3 {public static void main(String[] args) {int[] num = {100,4,200,1,3,2};int longgest = getLongestNum(num);System.out.println(longgest);}/*** 由于我们要枚举的数 xxx 一定是在数组中不存在前驱数 x−1 的,不然按照上面的分析我们会从 x−1x-1x−1 开始尝试匹配,因此我们每次在哈希表中检查是否存在 x−1x-1x−1 即能判断是否需要跳过了。** @param intData* @return*/private static int getLongestNum(int[] intData) {Set<Integer> intSet = new HashSet();for(int i:intData){intSet.add(i);}int longgest = 0;for(int j:intSet){if(!intSet.contains(j-1)){int curentData = j;int longgetIndex = 1;while (intSet.contains(curentData+1)){longgetIndex++;curentData++;}longgest = Math.max(longgest,longgetIndex);}}return longgest;}
}top4 移动零(双指针实现)
/*** 给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。** 请注意 ,必须在不复制数组的情况下原地对数组进行操作。*/
public class Top4 {private static void moveData(int[] num){/*我们创建两个指针 i 和 j,第一次遍历的时候指针 j 用来记录当前有多少 非0 元素。即遍历的时候每遇到一个 非0 元素就将其往数组左边挪,第一次遍历完后,j 指针的下标就指向了最后一个 非0 元素下标。
第二次遍历的时候,起始位置就从 j 开始到结束,将剩下的这段区域内的元素全部置为 0。*/if(num.length==0){return;}int j = 0;for(int i=0;i<num.length;i++){if(num[i]!=0){num[j]=num[i];j++;}}for(int i =j;i<num.length;i++){num[i] = 0;}}public static void main(String[] args) {int[] num = {1,0,2,3,4,0,5,9,0,7,8,0};moveData(num);for(int i = 0;i<num.length;i++){System.out.println(num[i]);}System.out.println("---------");int[] num2 = {5,0,2,3,4,0,5,9,0,7,8,0};moveDataTwo(num2);for(int i = 0;i<num2.length;i++){System.out.println(num2[i]);}}private static void moveDataTwo(int[] num){/*这里参考了快速排序的思想,快速排序首先要确定一个待分割的元素做中间点 x,然后把所有小于等于 x 的元素放到 x 的左边,大于 x 的元素放到其右边。这里我们可以用 0 当做这个中间点,把不等于 0(注意题目没说不能有负数)的放到中间点的左边,等于 0 的放到其右边。这的中间点就是 0 本身,所以实现起来比快速排序简单很多,我们使用两个指针 i 和 j,只要 nums[i]!=0,我们就交换 nums[i] 和 nums[j]*/if(num.length==0){return;}int j=0;for(int i=0;i<num.length;i++){if(num[i]!=0){int temp = num[i];num[i] = num[j];num[j++] = temp;}}}}相关文章:
最长连续数列,移动零)
java leetcodetop100 (3,4 )最长连续数列,移动零
top3 最长连续数列 给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。 * * 请你设计并实现时间复杂度为 O(n) 的算法解决此问题。 * * * * 示例 1: * * 输入:nums [100,…...
用Vite从零到一创建React+ts项目
方式一:使用create-react-app命令创建项目 1、使用以下命令初始化一个空的npm 项目 npm init -y 2、输入以下命令安装React npm i create-react-app ps:如果失败的话尝试(1:使用管理员身份执行命令(2:切换镜像重…...
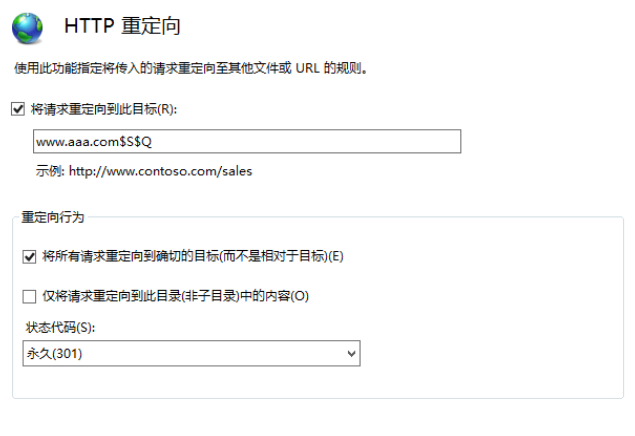
HTTP状态码301(永久重定向)不同Web服务器的配置方法
文章目录 301状态码通常在那些情况下使用301永久重定向配置Nginx配置301永久重定向Windows配置IIS301永久重定向PHP下的301重定向Apache服务器实现301重定向 301重定向是否违反相关法规?推荐阅读 当用户或搜索引擎向服务器发出浏览请求时,服务器返回的HT…...
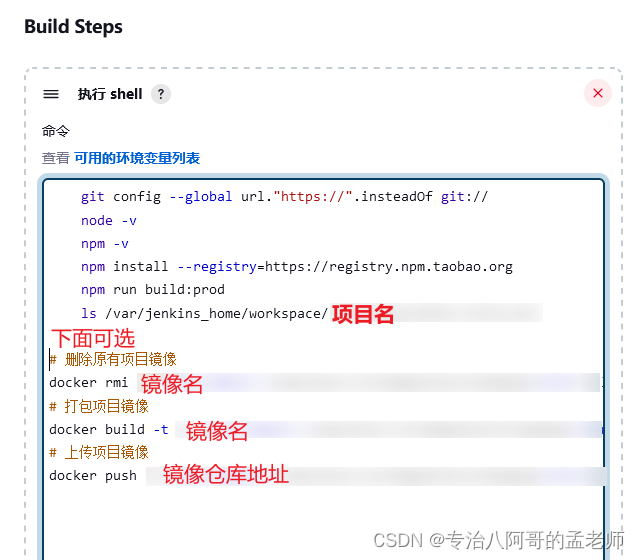
vue-element-admin项目部署 nginx动态代理 含Docker部署、 Jenkins构建
介绍三种方式: 1.直接部署到nginx中 2.用nginx docker镜像部署 3.使用Jenkins构建 1.直接用nginx部署 vue-element-admin项目下有两个.env文件,.env.production是生产环境的,.env.developpment是开发环境的 vue-element-admin默认用的是mock数…...
使用Python来写模拟Xshell实现远程命令执行与交互
一、模块 这里使用的是 paramiko带三方库 pip install paramiko二、效果图 三、代码实现(这里的IP,用户名,密码修改为自己对应服务器的) import paramiko import timeclass Linux(object):# 参数初始化def __init__(self, ip, us…...

mybatis 数据库字段为空or为空串 忽略条件过滤, 不为空且不为空串时才需nameParam过滤条件
name未配置视为不考虑name条件 select * from user where (( (ISNULL(name)) OR (name) ) OR name #{user.nameParam} ) 三个or语句 推荐这个 select * from user where ISNULL(name) OR name OR name #{user.nameParam} select * from user where ISNULL(name) OR …...
【玩玩Vue】通过vue-store实现枚举管理,用于下拉选项和中英文翻译等
原文作者:我辈李想 版权声明:文章原创,转载时请务必加上原文超链接、作者信息和本声明。 文章目录 一、store基础用法1.在src下新建store文件夹,在store下新建module文件夹2.在module下新建enums.js文件3.在store下新建getters.js…...

ISCSI:后端卷以LVM 的方式配置 ISCSI 目标启动器
写在前面 准备考试整理相关笔记博文内容涉及使用 LVM 做ISCSI 目标后端块存储 Demo理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。然后在心中坚守其一生,全心全意,永不停息。所有其它的路都是不完整的&#…...

八公山豆腐发展现状与销售对策研究
1.引言 八公山豆腐作为中国传统特色食品之一,一直以来备受人们的喜爱。然而,在现代社会中,由于消费者对于营养健康的追求以及市场竞争的加剧,八公山豆腐的市场份额逐渐缩小。因此,为了更好地推广和发展八公山豆腐&…...

排序算法-插入排序
属性 当插入第i(i>1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与array[i1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,原来位置上的元素顺序后移 直接插入排序…...
数码管显示)
多位数按键操作(闪烁)数码管显示
/*----------------------------------------------- 内容:按键加减数字,多个数码管显示 ------------------------------------------------*/ #include<reg52.h> //包含头文件,一般情况不需要改动,头文件包含特殊功能寄存…...

MyEclipse项目导入与导出
一、项目导出 1、右键选择项目名称,弹出菜单中选择“export”,如下图所示 2、选择“恶心“export”,弹出菜单如下;在“General“选项中,选择“File System”选项 3、点击“next”,进入保存位置选择界面&am…...
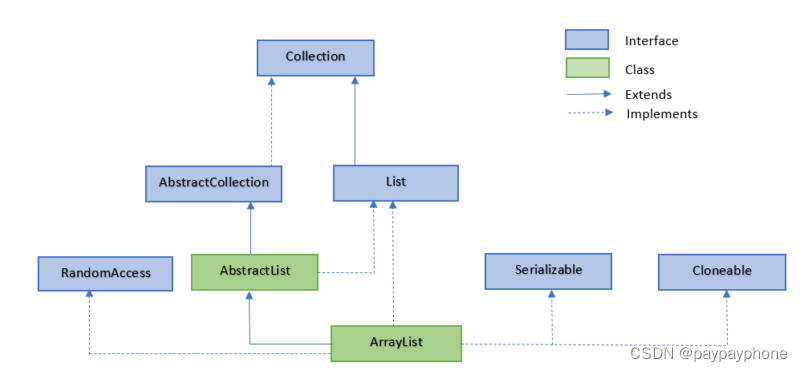
ArrayList和LinkedList
最近在刷回溯算法时,遇见了List<Integer> A new ArrayList<>(); LinkedList<Integer> B new LinkedList<>();这类型的表达方式 很好奇的问题是: 1、List<Integer> A new ArrayList<>();为什么是正确的写法 2…...

Linux 配置 Nginx 服务完整详细版
目录 前言 配置Nginx监听端口和服务器块 # 防DDoS配置 # 日志配置 # 设置服务器块 监听端口 网站根目录 默认文件 静态文件目录 图像文件目录 # 自定义错误页面 # 反向代理配置 # 配置SSL/TLS 1、获取SSL/TLS证书 2、安装证书 3、配置SSL/TLS # 配置SSL协议版本…...
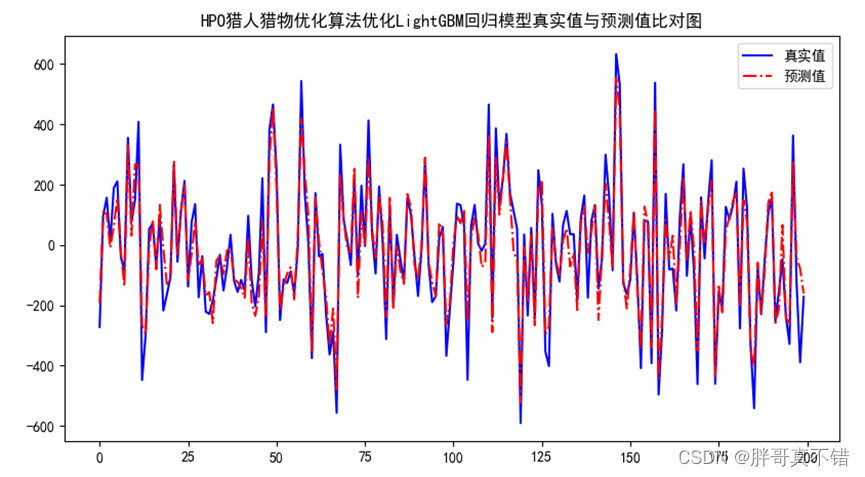
Python实现猎人猎物优化算法(HPO)优化LightGBM回归模型(LGBMRegressor算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 猎人猎物优化搜索算法(Hunter–prey optimizer, HPO)是由Naruei& Keynia于2022年提出的一种最新的…...

无涯教程-JavaScript - ODD函数
描述 ODD函数返回四舍五入到最接近的奇数整数的数字。 ODD函数是Excel中的15个舍入函数之一。 语法 ODD (number)争论 Argument描述Required/OptionalNumberThe value to round.Required Notes 无论数字的符号如何,值都将从零舍入到下一个奇数。如果number是一个奇数整数…...

Easyui里的datagrid嵌入select下拉框
问题: 想使用datagird里嵌入select下拉框,并在提交form表单时获取datagrid选中的每行数据里的每个下拉框选中的值。 解决方案: 其中economicIssuesSelect使用下拉框,重点关注 initEconomicIssues(row)方法。这里的方法需要传递ro…...

计算机专业毕业设计项目推荐03-Wiki系统设计与实现(JavaSpring+Vue+Mysql)
Wiki系统设计与实现(JavaSpringVueMysql) **介绍****系统总体开发情况-功能模块****各部分模块实现** 介绍 本系列(后期可能博主会统一为专栏)博文献给即将毕业的计算机专业同学们,因为博主自身本科和硕士也是科班出生,所以也比较了解计算机专业的毕业设…...

微服务的艺术:构建可扩展和弹性的分布式应用
文章目录 什么是微服务架构?微服务的设计原则1. 基于业务边界划分服务2. 松耦合和强内聚3. 自动化测试和部署4. 监控和日志5. 弹性设计 微服务的实施细节1. 服务发现示例代码:使用Consul进行服务发现 2. 负载均衡示例代码:Nginx配置负载均衡 …...

在PHP8中对数组进行排序-PHP8知识详解
在php8中,提供了丰富的排序函数,可以对数组进行排序操作。常见的排序函数如下几个:sort() 函数、rsort() 函数、asort() 函数、arsort() 函数、ksort() 函数、krsort() 函数、natsort()函数和natcascsort()函数。 1、sort() 函数:…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...

raid存储技术
1. 存储技术概念 数据存储架构是对数据存储方式、存储设备及相关组件的组织和规划,涵盖存储系统的布局、数据存储策略等,它明确数据如何存储、管理与访问,为数据的安全、高效使用提供支撑。 由计算机中一组存储设备、控制部件和管理信息调度的…...
