正则表达式学习和高级用法
以下所有的验证都在
在线验证
1. 起始符 /
正则表达式的起始符
2. 限定符
+
匹配前面的子表达式**1次或多次**。例如,zo+ 能匹配 "zo" 以及"zoo",但不能匹配 "z"。+等价于 {1,}。
?
匹配前面的子表达式**0次或1次**。例如,do(es)? 可以匹配 "do" 、 "does"、 "doxy" 中的 "do" 和 "does"。
? 等价于 {0,1}。
*
匹配前面的子表达式**0次或多次**。例如,zo* 能匹配 "z" 以及"zoo"。* 等价于 {0,}。
. 句点符
匹配除换行符外 /r 和 /n的所有字符,但一次只能匹配一个
{ }
{n}
n 是一个非负整数。匹配确定的 n 次。例如,o{2} 不能匹配 "Bob" 中的 o,但是能匹配 "food" 中的两个 o。
{n,}
n 是一个非负整数。至少匹配n 次。例如,o{2,} 不能匹配 "Bob" 中的 o,但能匹配 "foooood" 中的所有 o。o{1,} 等价于 o+。o{0,} 则等价于 o*。
{n,m}
m 和 n 均为非负整数,其中 n <= m。最少匹配 n 次且最多匹配 m 次。例如,o{1,3} 将匹配 "fooooood" 中的前三个 o。o{0,1} 等价于 o?。请注意在逗号和两个数之间不能有空格。
3. 普通字符
[ ]
所有的区间都会匹配一个结果返回
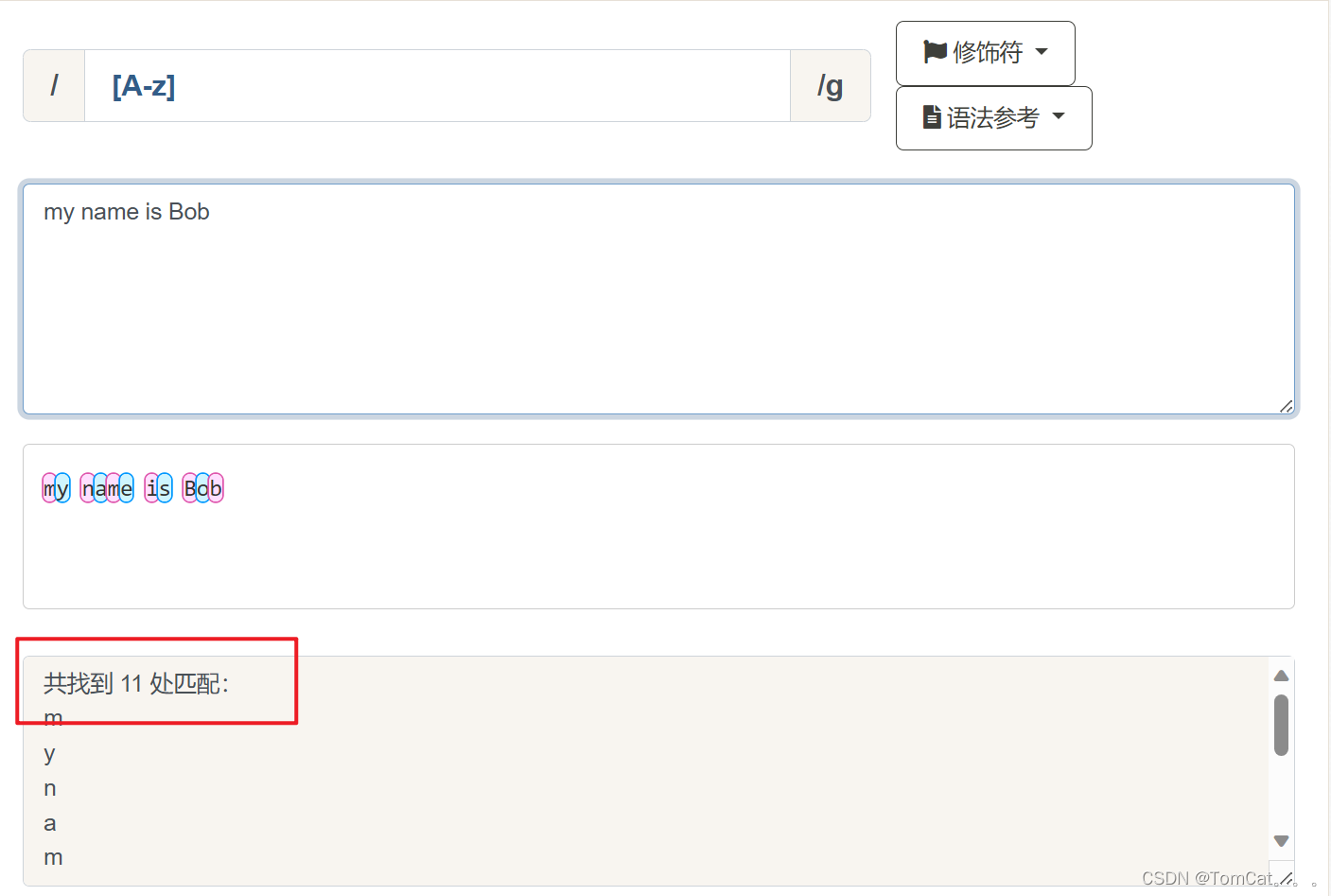
[ABC]
匹配包含在中括号中的所有字符,注意的是匹配的的字符不需要是连续的的,只要是在 [...]中的字符就行,相当于字典。
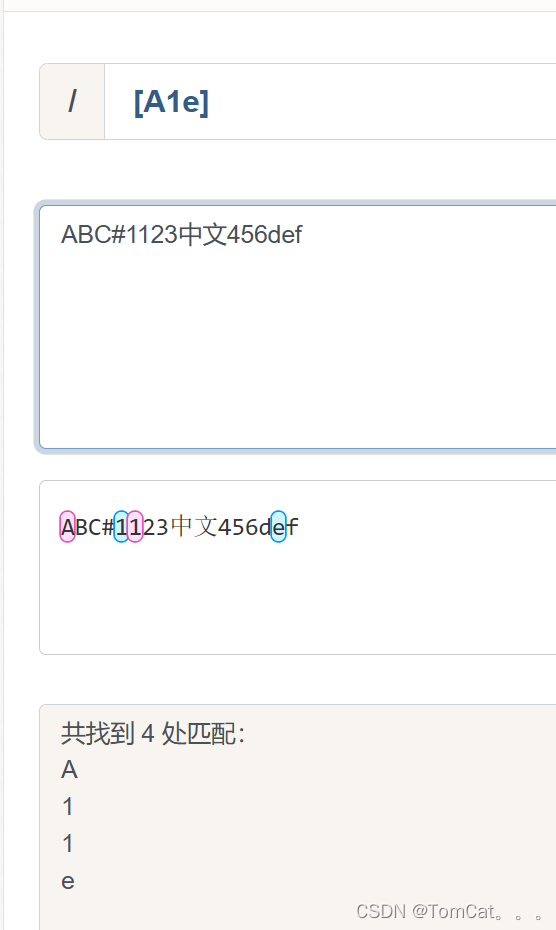
[^ABC ]
和[ABC] 是取反的操作,表示不包含的匹配
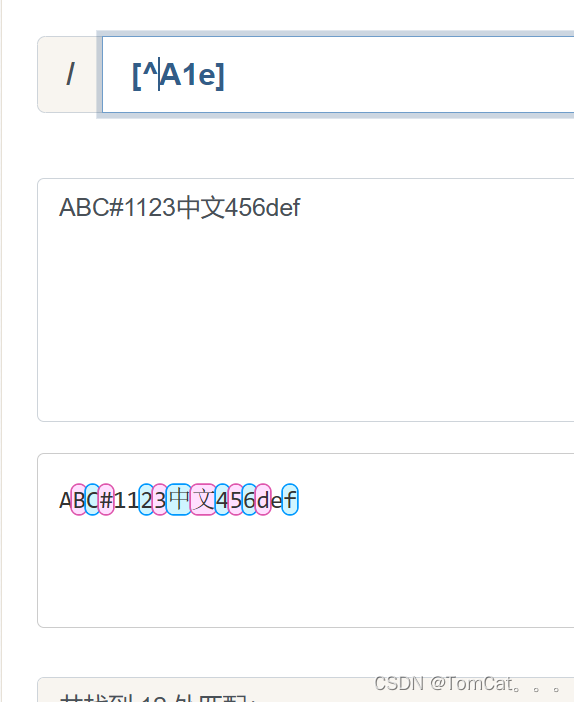
区间操作 [A-Za-z0-0]
匹配某一区间的所有包含字符 例如匹配所有的中文[\u4e00-\u9fa5] ,这里是通过Unicode
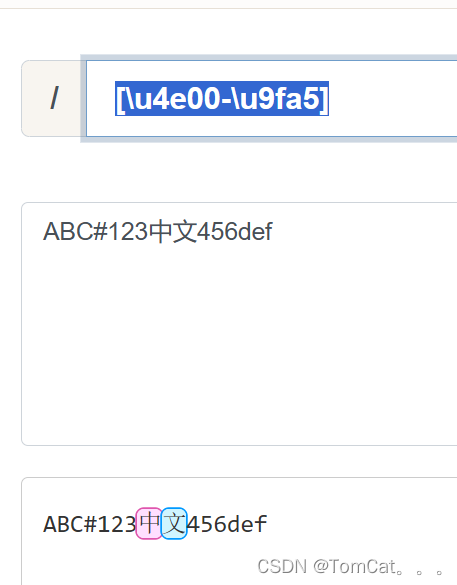
4. 元字符
\d \D
配置所有的数字字符, 大写的表示取反 0-9
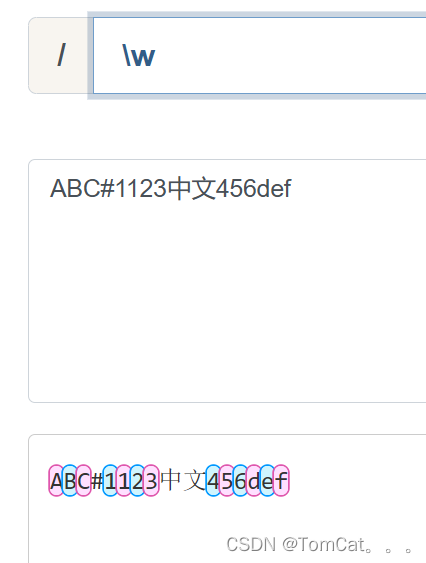
\w \W
匹配所有的 英文字母 + 数字 + 下划线, 只能匹配一个,如果要匹配多个需要用到 \w+
\s \S
匹配任何空白字符,包括空格、制表符、换页符等等。
5. 逻辑运算符
与运算 (...)
括号内的做为一个整体匹配
或运算符 |
指明两项之间的一个选择。要匹配 |,请使用 \|
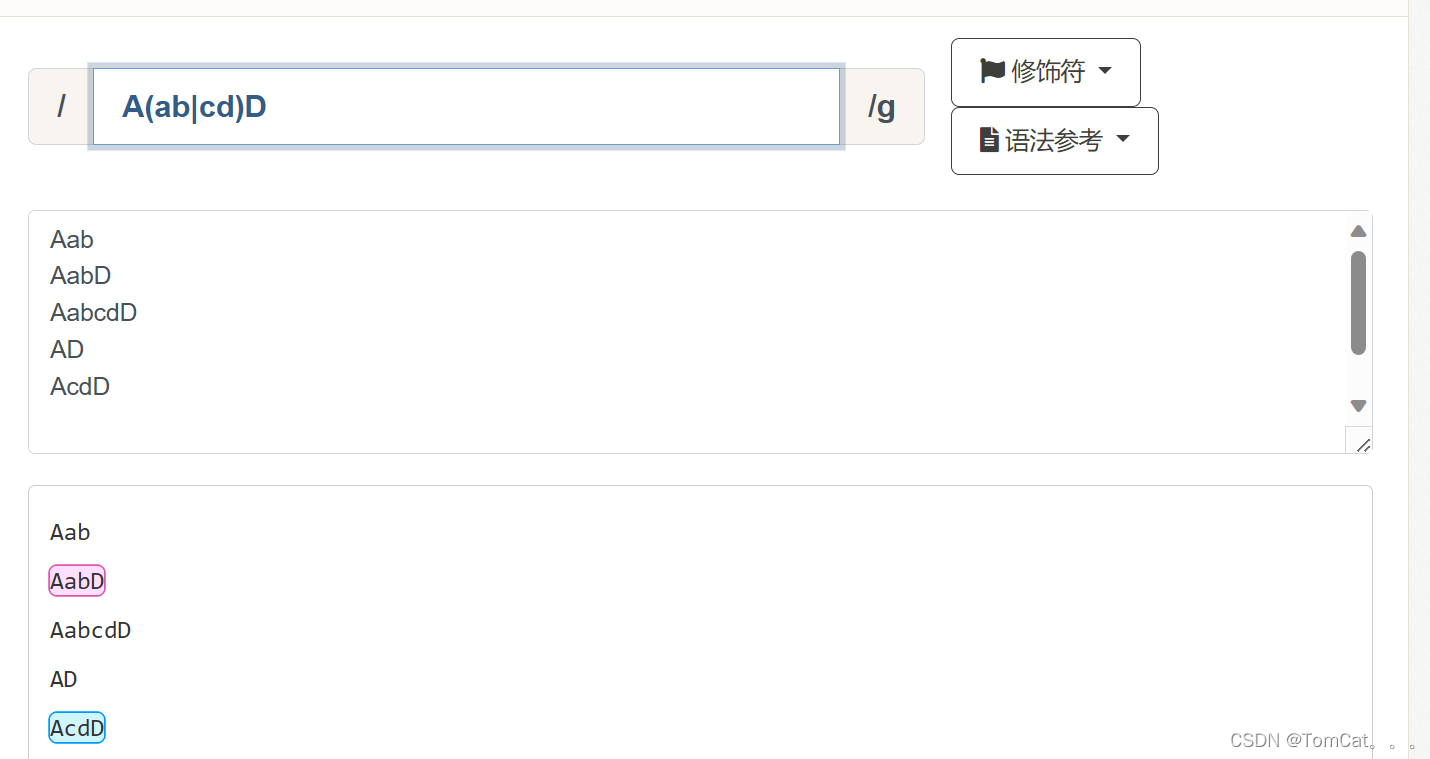
A(ab|cd)D 两个匹配一个
6. 定位符
$ 字符串结尾符
表示匹配的所有字符在句尾
^ 首字符匹配
在中括号中[ ] 表示取反
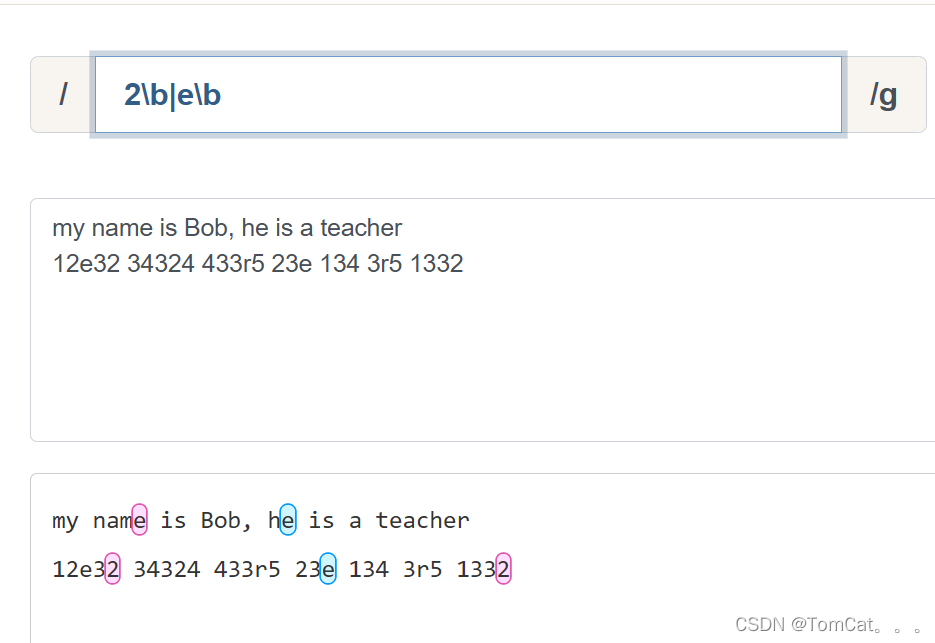
\b \B 边界匹配符
将两个空个之间的字符整体作为一个单词, 匹配边界包含某一特征的字符
7. 高级用法
贪婪匹配 or 懒惰匹配 ?
正则匹配的原则默认是按照贪婪匹配,表示尽可能多的匹配,也就是在满足条件的情况下,找到最长的。
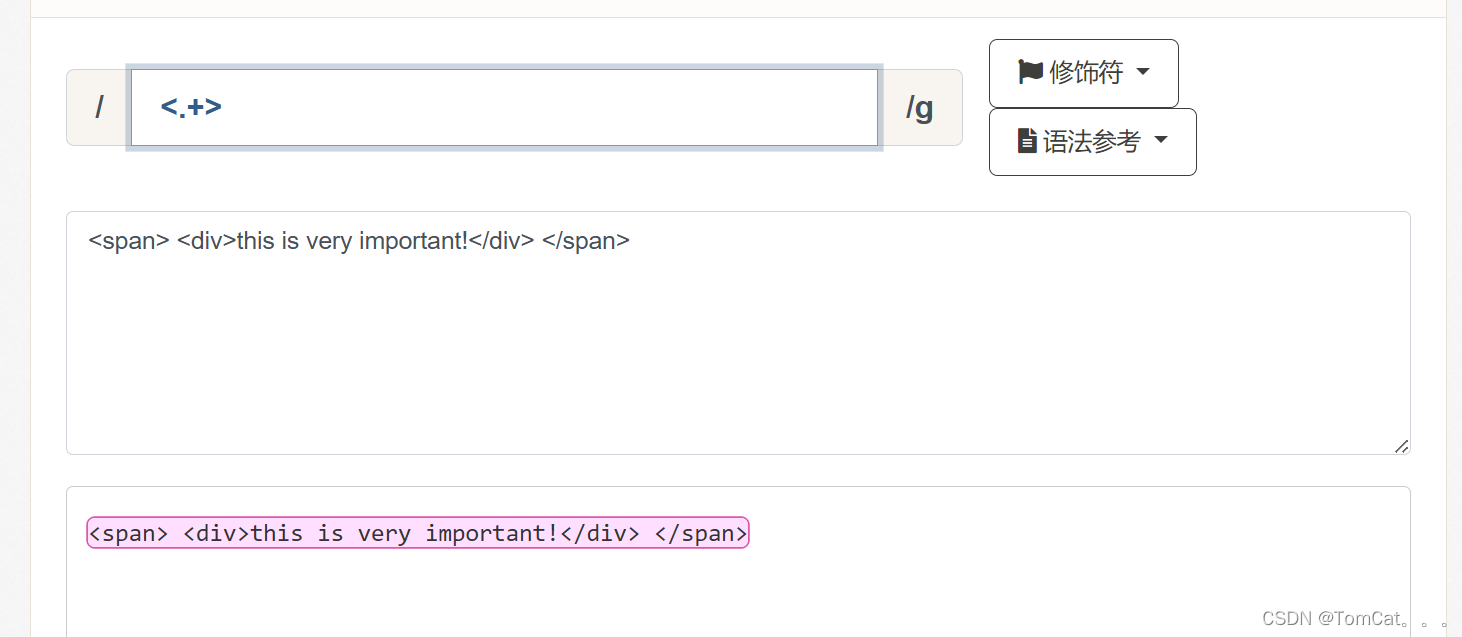
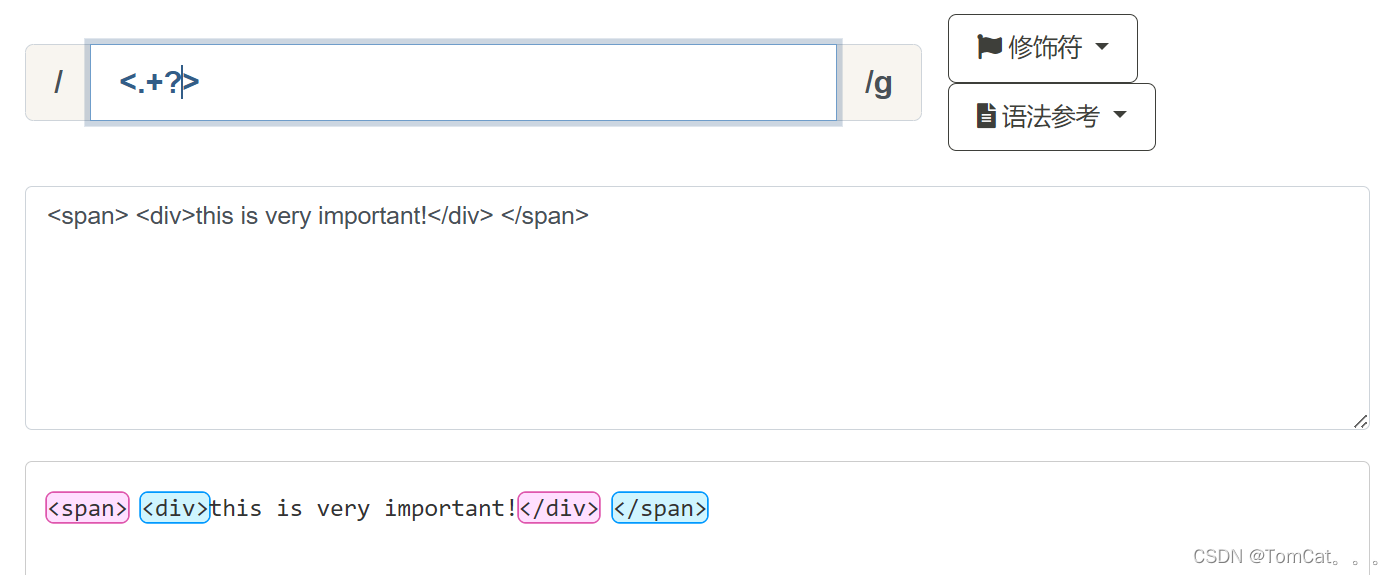
<span> <div>this is very important!</div> </span>
我们要匹配所有的html标签 我们用 <.+> ,结果发现匹配的并不是 按照 <span> 和 <div>
而是把所有的都返回了,原因就是默认采用了贪婪匹配。
如果我们用<.+?>表示我们用懒惰匹配,只要找到符合的就作为一个返回结果。
懒惰模式存在时对可匹配多个字符的操作符 例如
| 贪婪元字符 | 懒惰元字符 |
|---|---|
+ | +? |
* | *? |
{} | {}? |
修饰符
/i
ignore - 不区分大小写 将匹配设置为不区分大小写,搜索时不区分大小写: A 和 a 没有区别。
/g
g global - 全局匹配 查找所有的匹配项。
/m
m multi line - 多行匹配 使边界字符 ^ 和 $ 匹配每一行的开头和结尾,记住是多行,而不是整个字符串的开头和结尾。
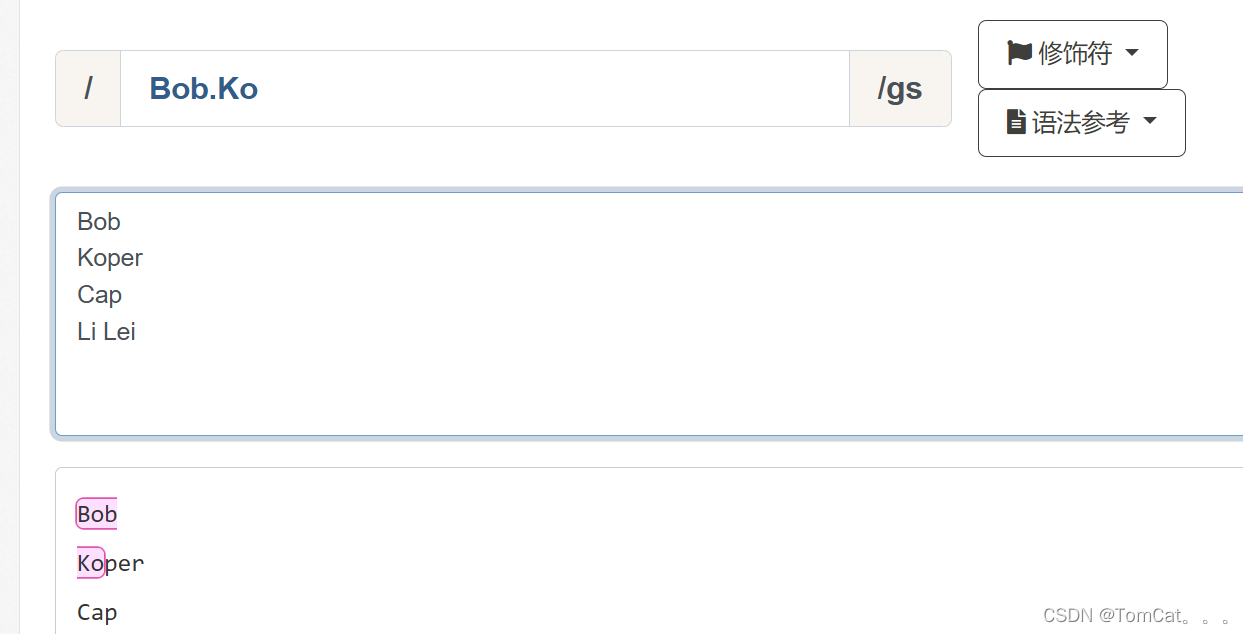
/s
特殊字符圆点. 中包含换行符 \n, 默认情况下的圆点 . 是匹配除换行符 \n 之外的任何字符,加上 s 修饰符之后,
. 中包含换行符 \n。
回溯引用
回溯引用指的是模式的后半部分引用在前半部分中定义的子表达式,且只能用来引用模式里的子表达式()子表达式即用元字符(和)括起来的部分)。简单理解,可以将回溯引用想象成对变量的引用。
使用
\1表示引用第1个子表达式,\2表示引用第2个子表达式,以此类推(通常,回溯引用从1开始匹配)
注意
由于子表达式是按照其在表达式中的相对位置来引用的,因此有个不好之处在于,一旦改变了子表达式的相对位置,很容易引起正则的回溯引用失效。
例子:
我们要匹配一个HTML标签 <h1>-<h6> 中的内容,我们用这样的正则<[Hh][1-6]>.*?</[Hh][1-6]>,这个可以匹配但是没有办法判断标签错误匹配的问题。
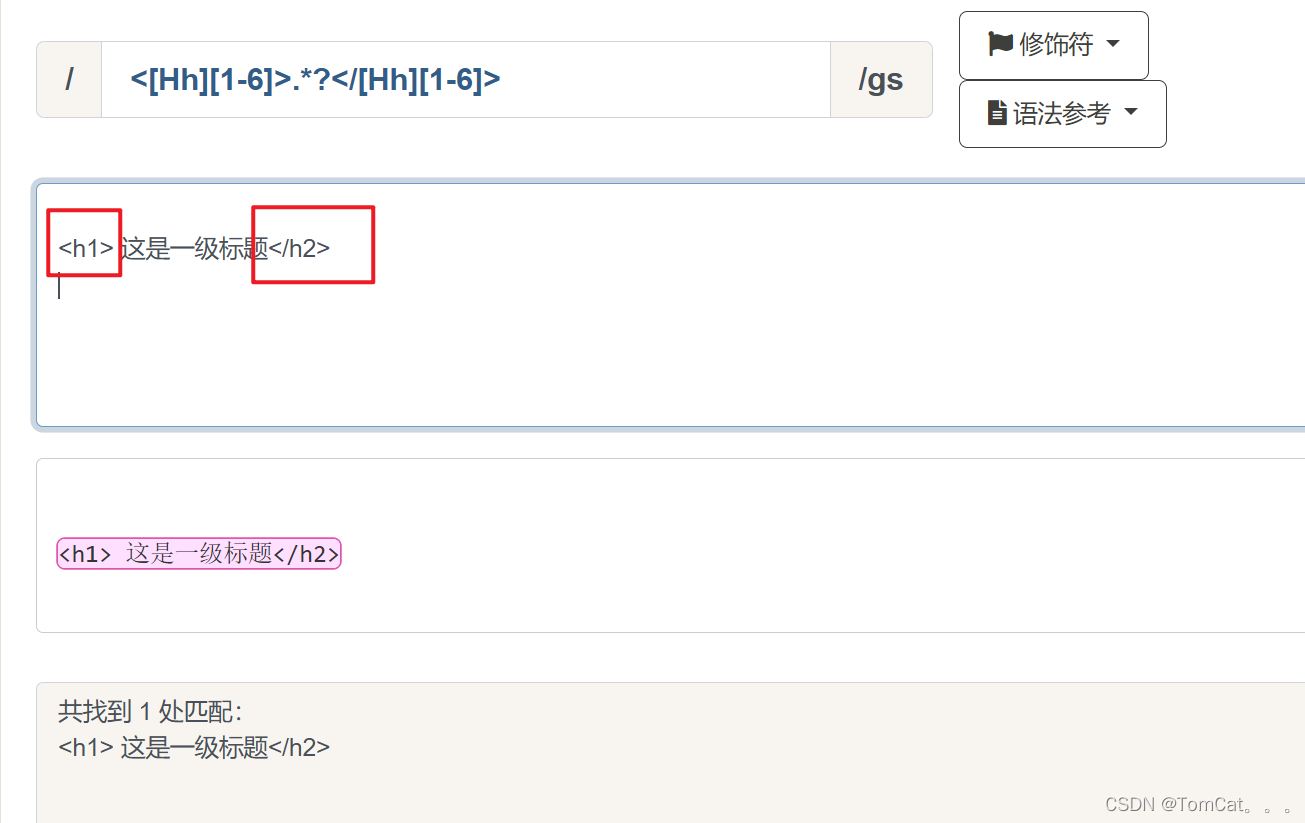
可以用回溯解决,主要时判断<h>标签前面的数字是否匹配, <[hH]([1-6])>.*?</[hH]\1>就可以解决。
替换操作符 $
$1、$2表达的是正则表达式中小括号(即分组)中的内容,$1是第一个小括号(分组)中的匹配结果,$2是第二个小括号(分组)中的匹配结果,以此类推。通常$1、$2用在替换操作中。如下:

前后查找
前后查找是查找具有某一条件的字符串
(正)向前查找 (?=)
如果我们想在一堆 URL 中拿到它们的协议名(scheme)
http://www.test.com
https://www.example.com
ftp://ftp.aaa.com
我们可能会使用.+: 来完成要求,但是该模式匹配的是 http:,https:,ftp:,要提取协议名我们还得对字符串做二次处理。所幸的是,使用向前查找.+(?=:) 就能够省去后面的冒号,其中子表达式(?=:) 表示找到: 就可以了,不把它包括在最终的匹配结果里。
(正)向后查找 (?<=)
除了?= 表示向前查找,还有很多正则表达式(JS不在其中。。。)也支持向后查找,操作符为 ?<=。同样地,来看一个例子:对于如下文本
ABC01: $23.45
HGG43: $5.31
如果我们想将其中的价格匹配出来(不含$),使用 [0-9.]+ 是不行的,因为它也会匹配出 01 和 43,这时候使用向后查找 (?<=\$)[0-9.]+ 问题就迎刃而解了。
前后取非查找 (负向查找) (?!) (?<!)
如果文本中我们只想匹配数量而不匹配金额:只匹配num 不匹配 $num,比如下面这个例子
I paid $30 for 100 apples,
50 orange, and 60 pears,
I saved $5 on this order.
\b(?<!\$)\d+\b 最终的匹配的结果是只包含那些不以 $ 开头的数值。
这个是所有操作符的总结
这时候可以取非
| 操作符 | 说明 |
|---|---|
(?=) | 正向前查找 |
(?<=) | 正向前查找 |
(?!) | 负向前查找 |
(?<!) | 负向后查找 |
嵌入条件
北美的电话号码格式是 (123)456-7890 和 123-456-7890,要匹配该模式,可能很容易就想到使用 \(?\d{3}\)?-?\d{3}-\d{4},但是该表达式也会匹配到非法的数据格式比如 (123-456-7890,这种情况我们就需要使用条件:如果电话号码里有一个 (,则第五个字符匹配 ),否则匹配 -。
嵌入条件的语法为:
(?(backreference)true-regex)
(?(backreference)true-regex|false-regex)
可以理解为:
if (backreference) { true-regex } else { false-regex }
分析这个模式,其中 (\()? 匹配一个可选的左括号,(?(1)\)|-) 是一个回溯引用条件,只有配对出现的括号才会被匹配。
相关文章:

正则表达式学习和高级用法
以下所有的验证都在 在线验证 1. 起始符 / 正则表达式的起始符2. 限定符 匹配前面的子表达式**1次或多次**。例如,zo 能匹配 "zo" 以及"zoo",但不能匹配 "z"。等价于 {1,}。 ? 匹配前面的子表达式**0次或1次**。例如…...
C# Onnx Yolov8 Fire Detect 火焰识别,火灾检测
效果 项目 代码 using Microsoft.ML.OnnxRuntime.Tensors; using Microsoft.ML.OnnxRuntime; using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System.Linq; using System.Text; using Syste…...
线程安全问题
目录 一、线程安全 二、线程安全问题 三、线程安全 1.同步代码块 2.同步方法 3.Lock锁 3.1常用方法: 3.2 死锁 3.3 练习: 四、生产者和消费者(线程通信问题) 一、线程安全 如果有多个线程在同时运行,而这些…...
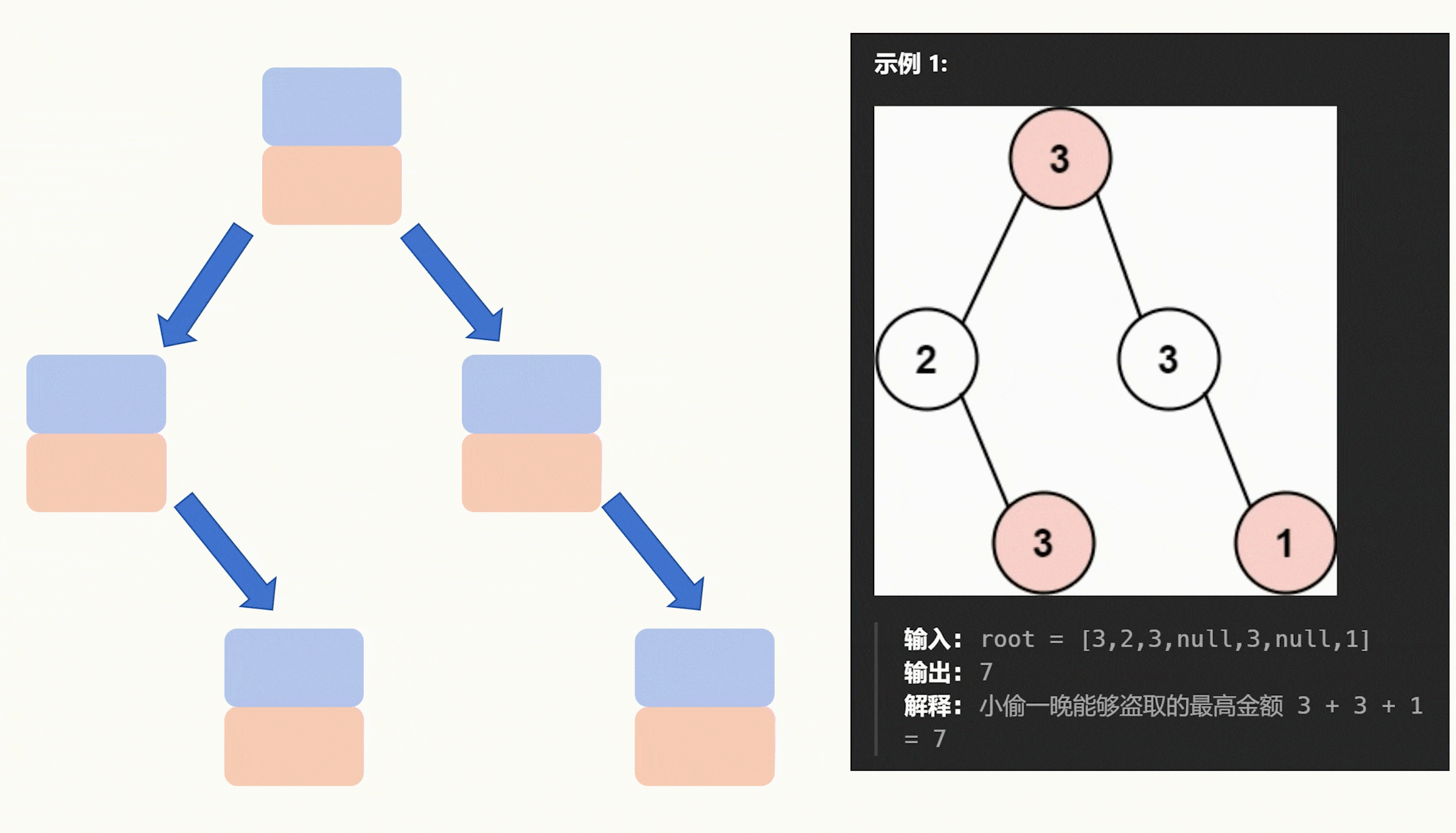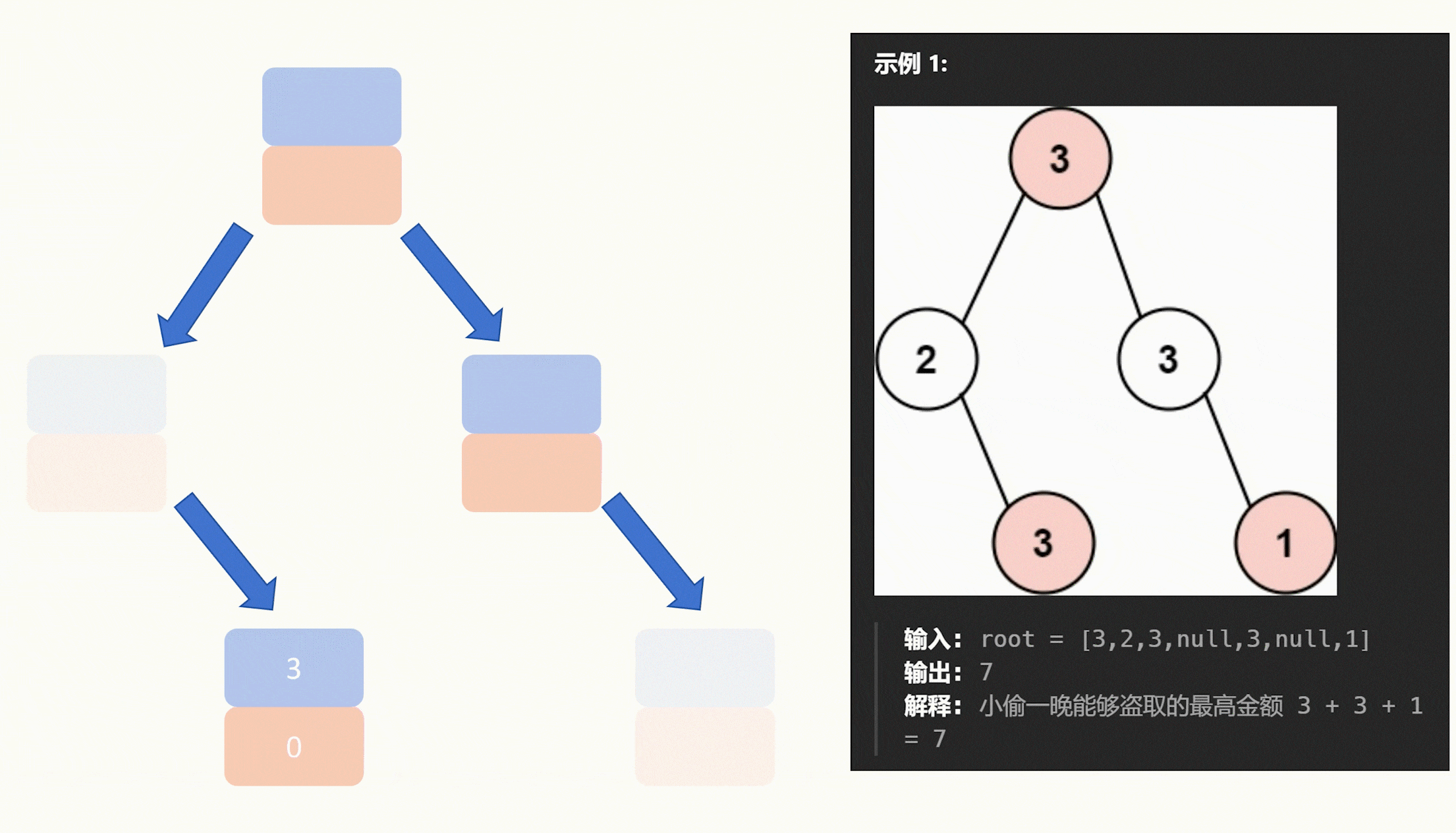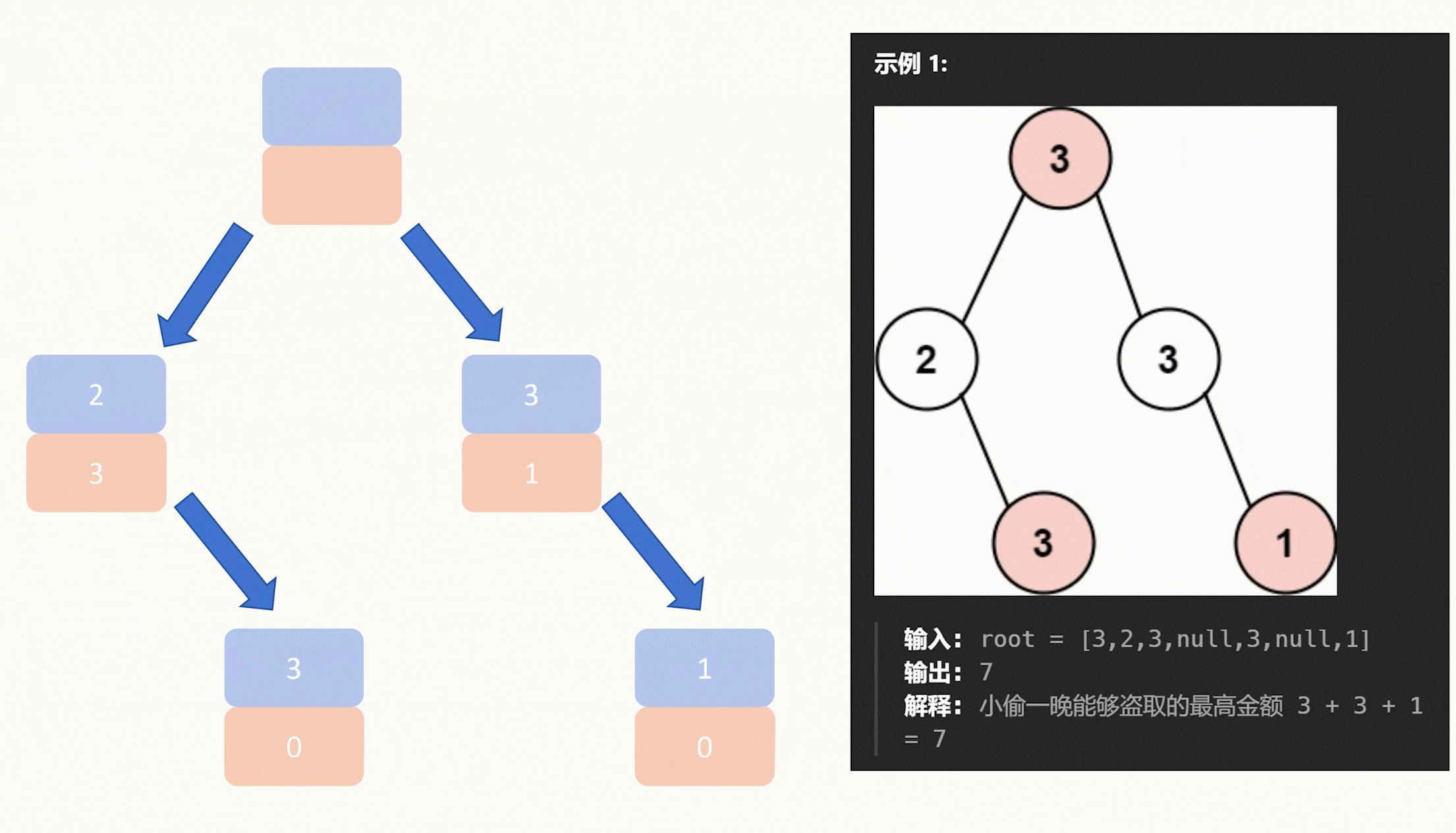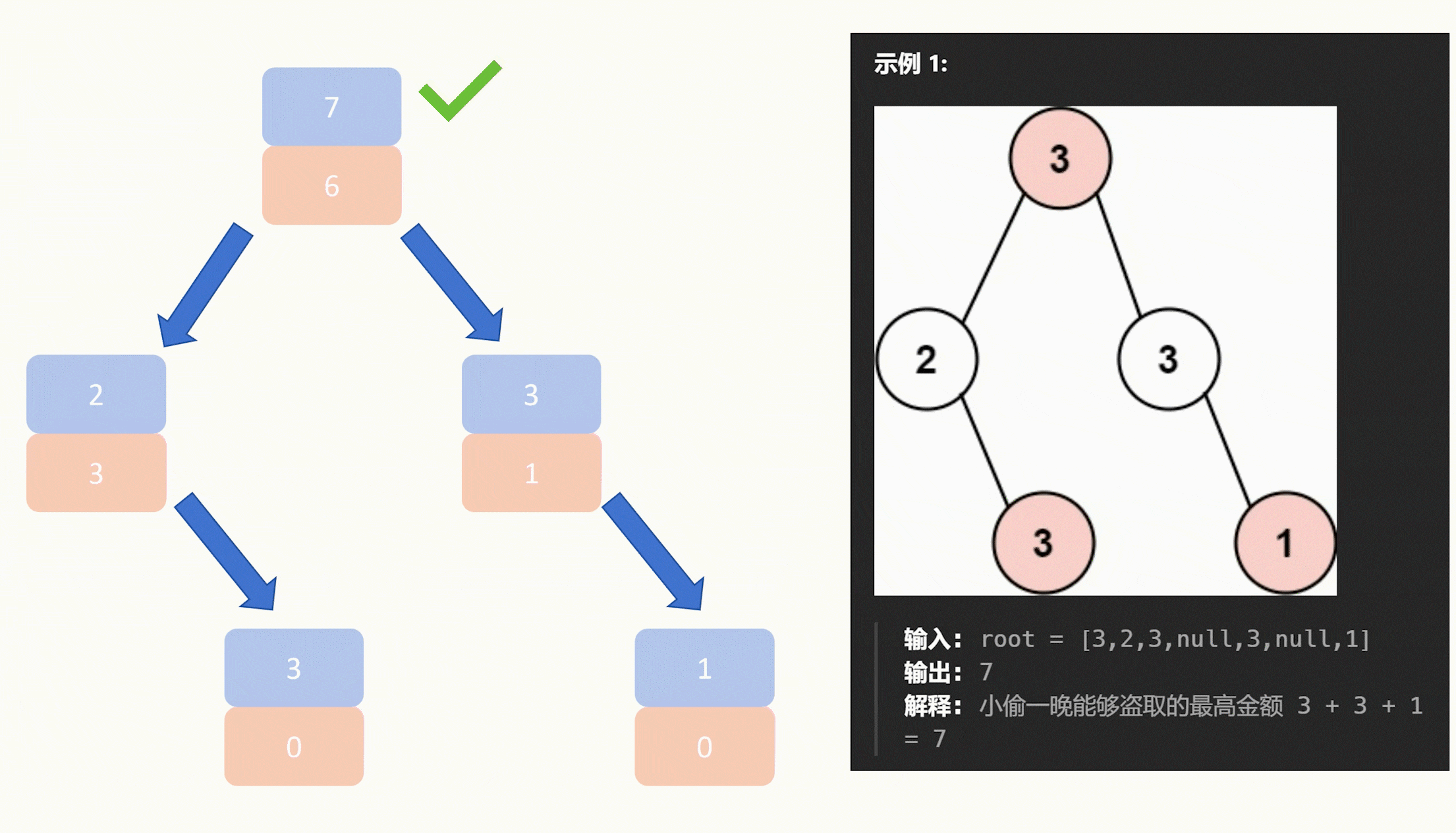
【力扣每日一题】2023.9.18 打家劫舍Ⅲ
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 今天是打家劫舍3,明天估计就是打家劫舍4了。 今天的打家劫舍不太一样,改成二叉树了,不过规则没有变&…...

Docker基础学习
Docker 学习目标: 掌握Docker基础知识,能够理解Docker镜像与容器的概念 完成Docker安装与启动 掌握Docker镜像与容器相关命令 掌握Tomcat Nginx 等软件的常用应用的安装 掌握docker迁移与备份相关命令 能够运用Dockerfile编写创建容器的脚本 能够…...
)
esbuild中文文档-路径解析配置项(Path resolution - Alias、Conditions)
文章目录 路径解析配置项 Path resolution别名 Alias条件解析 Conditionsconditions是如何工作的 结语 哈喽,大家好!我是「励志前端小黑哥」,我带着最新发布的文章又来了! 老规矩,小手动起来~点赞关注不迷路࿰…...

您的应用存在隐藏最近任务列表名称的行为,不符合华为应用市场审核标准
最近各家应用市场,唯独华为审核被拒了。。理由是您的应用存在隐藏最近任务列表名称的行为,不符合华为应用市场审核标准。 根据华为给出的视频,app在任务队列(也就是俗称的安卓多任务管理后台)不显示应用名。因为我们ap…...
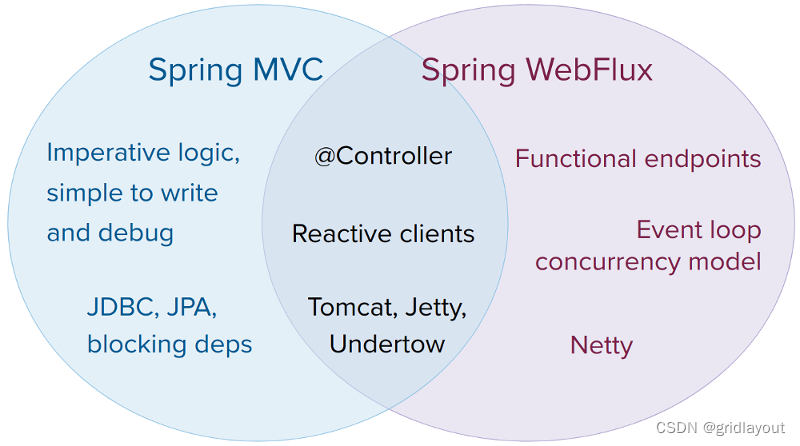
Spring的 webFlux 和 webMVC
看到一个测评文章,并发在300的时候webMVC 和 webFlux的处理能力不相上下, 当并发达到3000的时候, webFlux明显优于webMVC, 有图有真相, 我信了. webMVC 是 one-request-one thread 堵塞模式, flux是非阻塞模式, 是spring家族系列…...

【洛谷算法题】P5706-再分肥宅水【入门1顺序结构】
👨💻博客主页:花无缺 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 花无缺 原创 收录于专栏 【洛谷算法题】 文章目录 【洛谷算法题】P5706-再分肥宅水【入门1顺序结构】🌏题目描述🌏输入格式…...

android studio环境搭建让你的开发之旅更加简单
示例示例Android Studio环境搭建:下载并安装Android Studio:从官网下载Android Studio,然后双击安装文件,按照提示进行安装,安装完成之后,可以在桌面上找到Android Studio的快捷方式。 Android Studio环境…...

Java面试_并发编程_线程基础
Java面试_并发编程_线程基础 线程基础线程和进程的区别(出现频率: 3⭐)并行和并发的区别(出现频率: 2⭐)线程的创建(出现频率: 4⭐)线程的状态(出现频率: 4⭐)让线程按顺序执行(出现频率: 3⭐)notify()和notifyAll()有什么区别(出现频率: 2⭐)wait方法和sleep方法的区别(出现频…...
基于Java的高校实习管理系统设计与实现(亮点:实习记录、实习打分、实习作业,功能新颖、老师没见过、当场唬住!)
高校实习管理系统 一、前言二、我的优势2.1 自己的网站2.2 自己的小程序(小蔡coding)2.3 有保障的售后2.4 福利 三、开发环境与技术3.1 MySQL数据库3.2 Vue前端技术3.3 Spring Boot框架3.4 微信小程序 四、功能设计4.1 主要功能描述 五、系统主要功能5.1…...

傅里叶变换
傅里叶变换常用于缺陷检测项目,对于一些背景偏暗,对比度不明显的场景,傅里叶变换可以起到提升对比度的效果。傅里叶变换从频域角度来处理,对于一些图像像素尺寸大的图像,算法时间往往时间达到1s以上,对于一…...

Vue Grid Layout -️ 适用Vue.js的栅格布局系统,在vue3+上使用
文章目录 1、官网简介2、在vue3中使用1)、需要导入vue3支持的版本插件2)、在mian.js里引入:3)、在组件中使用 3、layout布局的计算逻辑4、 gridLayout 的属性 该栅格系统目前对 vue2 的支持是最好的,vue3 是需要用插件支持的,会在小节详细讲解…...
无法加载React Developer Tools(v4.28.0))
Electron(v26.2.1)无法加载React Developer Tools(v4.28.0)
一开始按照electron官网上的 开发者工具扩展 教程设置React Developer Tools时,重启项目后并没有按照预期成功加载React Developer Tools,而且控制台报错: Permission scripting is unknown or URL pattern is malformed.查了下原因是因为Re…...

网站降权的康复办法(详解百度SEO数据分析)
随着搜索引擎算法的不断升级,很多网站在SEO优化过程中遭遇到降权的情况。如果您的网站也遭遇到了类似的问题,不必惊慌失措。本文将为您详细介绍网站降权恢复的方法,包括百度SEO数据分析、网站收录少的5个原因、网站被降权的6个因素以及百度SE…...

非对称加密、解密原理及openssl中的RSA示例代码
一、【原理简介】非对称加密 非对称加密,也被称为公钥加密,其中使用一对相关的密钥:一个公钥和一个私钥。公钥用于加密数据,私钥用于解密数据。公钥可以公开分享,而私钥必须保密。 密钥生成: 当一个用户或设备希望使用…...
基于springboot漫画管理系统springboot001
摘 要 随着信息技术和网络技术的飞速发展,人类已进入全新信息化时代,传统管理技术已无法高效,便捷地管理信息。为了迎合时代需求,优化管理效率,各种各样的管理系统应运而生,各行各业相继进入信息管理时代&…...

【探索C++】string类详解
(꒪ꇴ꒪ ),Hello我是祐言QAQ我的博客主页:C/C语言,数据结构,Linux基础,ARM开发板,网络编程等领域UP🌍快上🚘,一起学习,让我们成为一个强大的攻城狮࿰…...
python 第一次作业
1.使用turtle换一个五环 2.设计这样一个程序:输入一个数字 判断它是不是一个质数 使用turtle换一个五环: >>> import turtle #导入模块 >>> turtle.width(10) #设置圆圈宽度 >>> turtle.color("blue&qu…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
