当前位置： 首页 > news >正文

傅里叶变换

news 2026/2/9 6:44:34

傅里叶变换常用于缺陷检测项目，对于一些背景偏暗，对比度不明显的场景，傅里叶变换可以起到提升对比度的效果。傅里叶变换从频域角度来处理，对于一些图像像素尺寸大的图像，算法时间往往时间达到1s以上，对于一些快速检测场景而言，此方法需要进一步改进。

*傅里叶变换是将空间域图像转换为频域图像
*图像处理作用：
*1.图像增强与图像去噪，绝对大部分噪音都是图像高频分量，通过低通滤波器可以滤除高频——噪声
*2.边缘检测——提取图像高频分量
*3.图像压缩可以直接通过傅里叶系数来压缩数据（大部分能量分布在低频谱段，对压缩传输有利，运算次数减少，节省时间）

detect_indent_fft.hdev

 

相关文章：

傅里叶变换

傅里叶变换常用于缺陷检测项目，对于一些背景偏暗，对比度不明显的场景，傅里叶变换可以起到提升对比度的效果。傅里叶变换从频域角度来处理，对于一些图像像素尺寸大的图像，算法时间往往时间达到1s以上，对于一…...

编程日记 2023/9/19 10:45:39

Vue Grid Layout -️ 适用Vue.js的栅格布局系统，在vue3+上使用

文章目录 1、官网简介2、在vue3中使用1)、需要导入vue3支持的版本插件2)、在mian.js里引入：3)、在组件中使用 3、layout布局的计算逻辑4、 gridLayout 的属性 该栅格系统目前对 vue2 的支持是最好的，vue3 是需要用插件支持的，会在小节详细讲解…...

编程日记 2023/9/19 10:42:36

Electron(v26.2.1)无法加载React Developer Tools(v4.28.0)

一开始按照electron官网上的 开发者工具扩展 教程设置React Developer Tools时，重启项目后并没有按照预期成功加载React Developer Tools，而且控制台报错： Permission scripting is unknown or URL pattern is malformed.查了下原因是因为Re…...

编程日记 2023/9/19 10:41:34

网站降权的康复办法（详解百度SEO数据分析）

随着搜索引擎算法的不断升级，很多网站在SEO优化过程中遭遇到降权的情况。如果您的网站也遭遇到了类似的问题，不必惊慌失措。本文将为您详细介绍网站降权恢复的方法，包括百度SEO数据分析、网站收录少的5个原因、网站被降权的6个因素以及百度SE…...

编程日记 2023/9/19 10:40:33

非对称加密、解密原理及openssl中的RSA示例代码

一、【原理简介】非对称加密 非对称加密，也被称为公钥加密，其中使用一对相关的密钥：一个公钥和一个私钥。公钥用于加密数据，私钥用于解密数据。公钥可以公开分享，而私钥必须保密。 密钥生成: 当一个用户或设备希望使用…...

编程日记 2023/9/19 10:39:32

基于springboot漫画管理系统springboot001

摘 要 随着信息技术和网络技术的飞速发展，人类已进入全新信息化时代，传统管理技术已无法高效，便捷地管理信息。为了迎合时代需求，优化管理效率，各种各样的管理系统应运而生，各行各业相继进入信息管理时代&…...

编程日记 2023/9/19 10:37:30

【探索C++】string类详解

(꒪ꇴ꒪ )，Hello我是祐言QAQ我的博客主页：C/C语言，数据结构，Linux基础，ARM开发板，网络编程等领域UP🌍快上🚘，一起学习，让我们成为一个强大的攻城狮&#xff0…...

编程日记 2023/9/19 10:36:29

python 第一次作业

1.使用turtle换一个五环 2.设计这样一个程序：输入一个数字 判断它是不是一个质数 使用turtle换一个五环： >>> import turtle #导入模块 >>> turtle.width(10) #设置圆圈宽度 >>> turtle.color("blue&qu…...

编程日记 2023/9/19 10:32:25

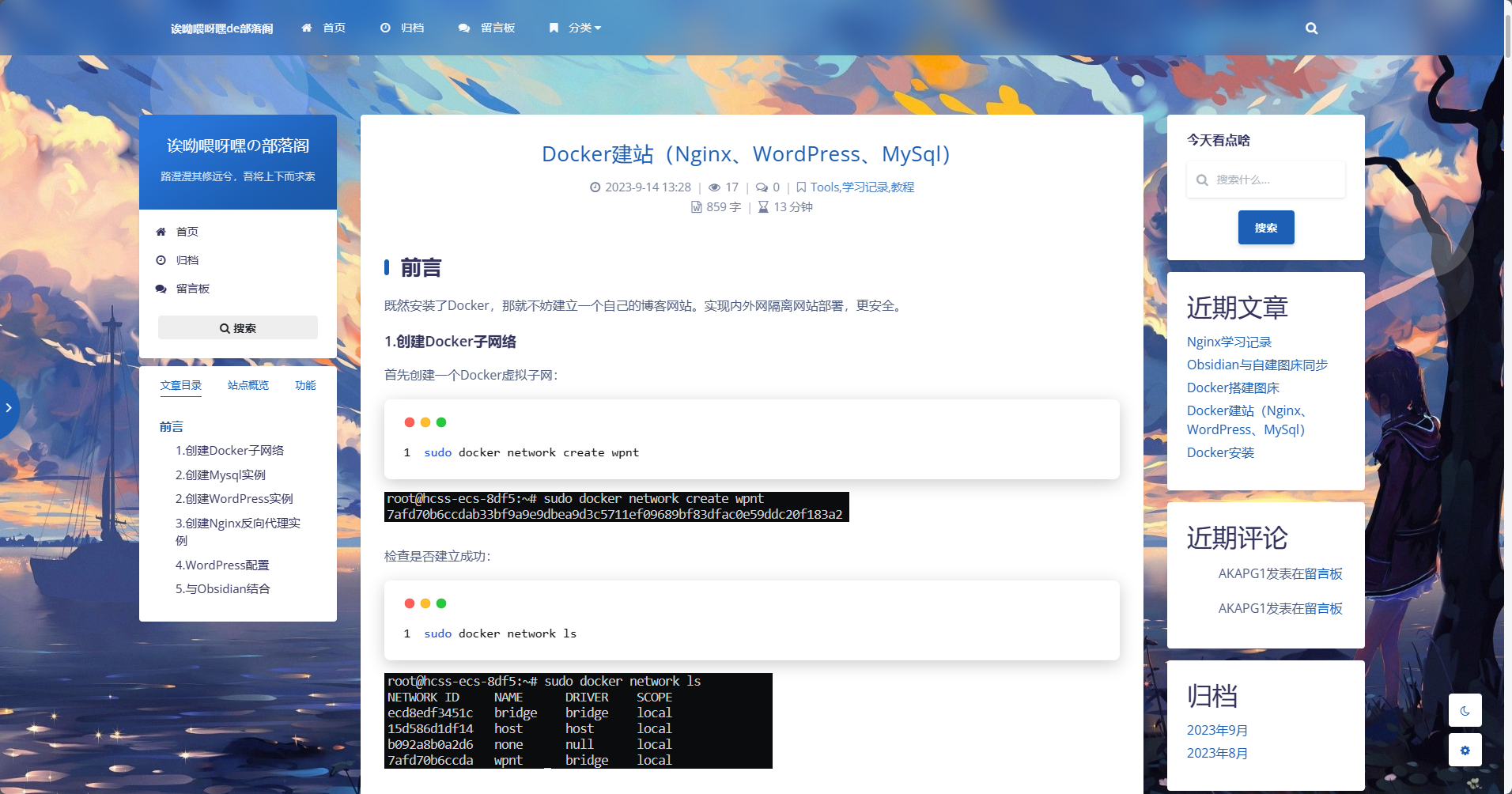
个人博客网站一揽子：Docker建站（Nginx、Wordpress、MySql）

前言 既然安装了Docker，那就不妨建立一个自己的博客网站。实现内外网隔离网站部署，更安全。 1.创建Docker子网络 首先创建一个Docker虚拟子网： sudo docker network create wpnt检查是否建立成功： sudo docker network ls最后…...

编程日记 2023/9/19 10:31:24

Unity 课时 4 : No.4 模拟面试题

课时 4 : No.4 模拟面试题 C# 1. 请说明字符串中 string str null string str “” string str string.Empty 三者的区别 第一个未作初始化没有值, 第二个为空字符串, 答案： str null 在堆中没有分配内存地址 str "" 和 string.Empty 一样都是…...

编程日记 2023/9/19 10:29:21

Golang 基础面试题 01

Golang 面试题合集.png 背景 在之前的文章中分享了 k8s 相关的面试题，本文我们重点来讨论和 k8s 密切相关的 Go 语言面试题。 这几年随着云原生的兴起，大部分后端开发者，特别是 Java 开发者都或多或少的想学习一些 Go 相关的技能，…...

编程日记 2023/9/19 10:26:19

007-第一代软件需求整理

第一代软件需求整理 文章目录 第一代软件需求整理项目介绍需求来源需求来源1：竞品软件分析需求来源2：医生（市场）需求来源3：项目组内部需求来源4：软件组内部需求来源5：软件开发成员需求来源6&…...

编程日记 2023/9/19 10:25:18

XMLHttpRequest介绍

目录 一、介绍1.创建 XMLHttpRequest2.初始化3.发送请求4.获取响应5.响应类型 二、发送GET请求示例三、发送POST请求示例四、发送POST请求下载文件示例五、发送POST请求上传文件示例 一、介绍 1.创建 XMLHttpRequest let xhr new XMLHttpRequest();2.初始化 xhr.open(metho…...

编程日记 2023/9/19 10:21:14

阿里云无影云电脑和传统PC有什么区别？

阿里云无影云电脑和传统电脑PC有什么区别？区别大了，无影云电脑是云端的桌面服务，传统PC是本地的硬件计算机，无影云电脑的数据是保存在云端，本地传统PC的数据是保存在本地客户端，阿里云百科分享阿里云无影云…...

编程日记 2023/9/19 10:19:12

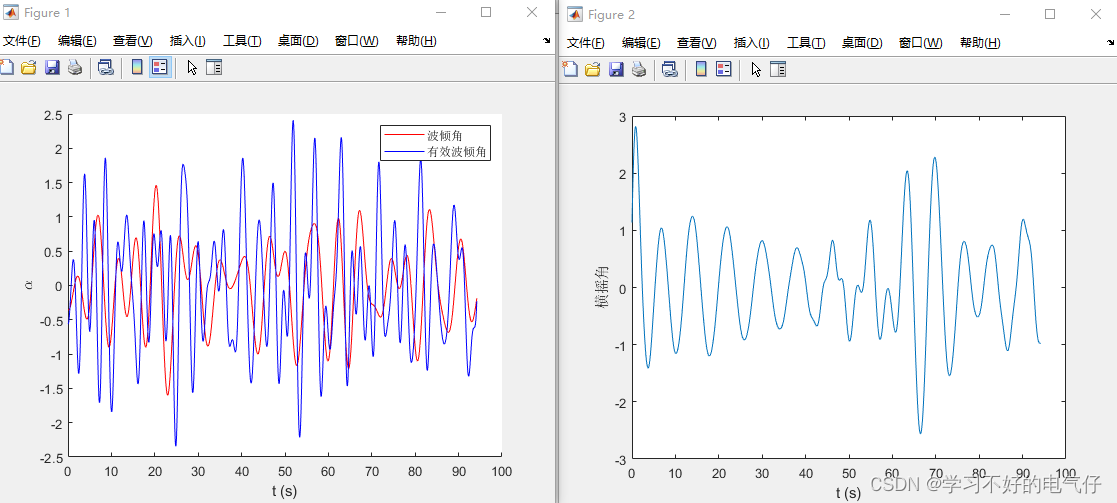
基于matlab实现的船舶横摇运动仿真程序

完整程序： clc clear syms w we; w0.4:0.05:1.6;mu90;v6;%kb1;kt1;%航速6m/s，航向90度，即横浪，cos(90)0 T3;B10;Sw0.785;%船宽10米，吃水3米,水线面系数假设为0.785 weww.^2.*v/9.8; for i1:24 delta_we(i)we(i1)-…...

编程日记 2023/9/19 10:14:07

Java手写二叉索引树和二叉索引树应用拓展案例

Java手写二叉索引树和二叉索引树应用拓展案例 1. 算法思维导图 以下为二叉索引树的实现原理的思维导图，使用Mermanid代码表示： #mermaid-svg-raMRIu7t3H33MKh1 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#…...

编程日记 2023/9/19 10:12:05

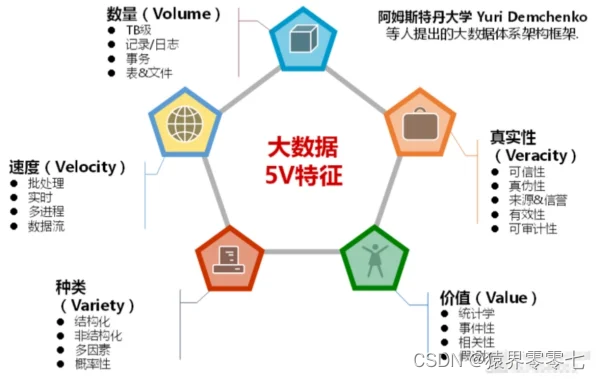
大数据知识点之大数据5V特征

大数据的特征可以浓缩为五个英文单词，Volume(大量）、Variety(多样性）、Velocity(速度）、Value(价值）、Veracity(准确性）。因为是5个特征都是以“V”开头的英文单词，又叫大数据5V特征。 概述&…...

编程日记 2023/9/19 10:11:04

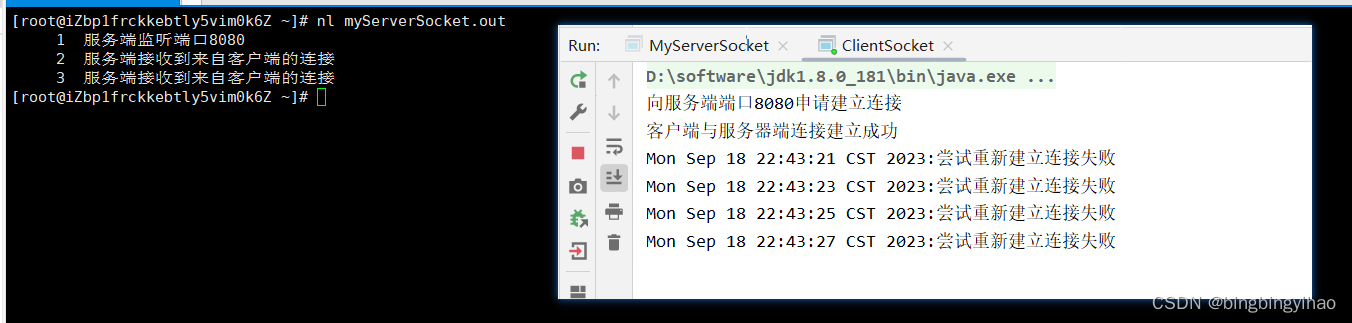
Java的Socket通信的断网重连的正确写法

Java的Socket通信的断网重连的正确写法 Socket通信的断网重连介绍客户端与服务端源码演示截图本地演示服务器演示演示截图 总结 Socket通信的断网重连介绍 针对于已经建立通信的客户端与服务器，当客户端与服务器因为网络问题导致网络不通而断开连接了或者由于服务器…...

编程日记 2023/9/19 10:10:03

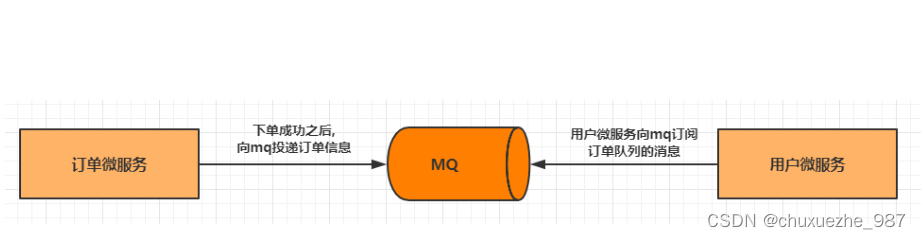
Rocketmq--消息发送和接收演示

使用Java代码来演示消息的发送和接收 <dependency><groupId>org.apache.rocketmq</groupId><artifactId>rocketmq-spring-boot-starter</artifactId><version>2.0.2</version> </dependency> 1 发送消息 消息发送步骤: 创建…...

编程日记 2023/9/19 10:09:02

ArcGIS Pro将SHP文件转CAD并保留图层名称

相信大家应该都使用过ArcGIS将SHP文件转CAD格式&#xff0c;转换过后所有的要素都在一个图层内&#xff0c;那么有没有办法将SHP文件某个字段的值作为CAD的图层名字呢&#xff0c;答案是肯定的&#xff0c;这里就为大家介绍一下ArcGIS Pro转CAD文件并且保留图层名称的方法&…...

编程日记 2023/9/19 10:05:59

HTML 语义化

目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案&#xff1a; 语义化标签&#xff1a; <header>&#xff1a;页头<nav>&#xff1a;导航<main>&#xff1a;主要内容<article>&#x…...

编程新知 2026/1/15 21:24:41

Linux链表操作全解析

Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表&#xff1f;1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

编程新知 2025/12/3 20:14:32

Qt Widget类解析与代码注释

#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码&#xff0c;写上注释 当然可以&#xff01;这段代码是 Qt …...

编程新知 2025/11/29 21:00:30

Python爬虫实战：研究feedparser库相关技术

1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代，互联网上存在着海量的信息资源。RSS（Really Simple Syndication）作为一种标准化的信息聚合技术，被广泛用于网站内容的发布和订阅。通过 RSS，用户可以方便地获取网站更新的内容，而无需频繁访问各个网站。 然而，互联网…...

编程新知 2025/8/18 9:54:31

系统设计 --- MongoDB亿级数据查询优化策略

系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log&#xff0c;共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题&#xff0c;不能使用ELK只能使用…...

编程新知 2026/1/4 3:47:09

STM32标准库-DMA直接存储器存取

文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA&#xff08;Direct Memory Access&#xff09;直接存储器存取 DMA可以提供外设…...

编程新知 2026/1/26 10:55:51

Java多线程实现之Callable接口深度解析

Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

编程新知 2026/1/25 6:36:06

CRMEB 框架中 PHP 上传扩展开发：涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云

目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

编程新知 2025/12/30 22:56:56

高防服务器能够抵御哪些网络攻击呢？

高防服务器作为一种有着高度防御能力的服务器&#xff0c;可以帮助网站应对分布式拒绝服务攻击&#xff0c;有效识别和清理一些恶意的网络流量&#xff0c;为用户提供安全且稳定的网络环境&#xff0c;那么&#xff0c;高防服务器一般都可以抵御哪些网络攻击呢&#xff1f;下面…...

编程新知 2025/9/3 19:14:38

Pinocchio 库详解及其在足式机器人上的应用

Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库&#xff0c;专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性&#xff0c;并提供了一个通用的框架&…...

编程新知 2025/11/28 5:32:31