【张兔兔送书第一期:考研必备书单】
考研书单必备
- 《数据结构与算法分析》
- 《计算机网络:自顶向下方法》
- 《现代操作系统》
- 《深入理解计算机系统》
- 《概率论基础教程(原书第10版》
- 《线性代数(原书第10版)》
- 《线性代数及其应用》
- 赠书活动
八九月的朋友圈刮起了一股晒通知书潮,频频有大佬晒出“研究生入学通知书”,看着让人既羡慕又焦虑。果然应了那句老话——比你优秀的人,还比你努力。
心里痒痒,想考研的技术人儿~别再犹豫了。小编咨询了一大波上岸的大佬,这份备考书单给大家参考。
专业课(此处特指408,全称计算机专业基础综合) 知识点超级多,题目灵活,数据结构、计算机网络、操作系统、计算机组成原理这四门课随便拿出来一门都可以出一套独立的考研卷,下面这几本重磅级图书可一定要啃透了…
《数据结构与算法分析》

《数据结构与算法分析——C语言描述(原书第2版》典藏版》
本书被评为20世纪顶尖的30部计算机著作之一
推荐语:国内外数据结构与算法分析方面的经典教材!详细介绍当前流行的论题和新的变化,讨论了算法设计技巧,并在研究算法的性能、效率上有独树一帜的技巧。
《计算机网络:自顶向下方法》

《计算机网络:自顶向下方法(原书第8版) 》
数十万读者选用的计算机网络入门教程
推荐语:经典教材全新升级,全球数百所高校选用,被译为14种语言畅销全球。
《现代操作系统》
《现代操作系统(原书第4版》
操作系统领域经典教材
推荐语:被国内外数百所学校选作教材。第4版对知识点进行了全面更新,反映了当代操作系统的发展与动向。
《深入理解计算机系统》

《深入理解计算机系统(原书第3版)》
一本能让程序员脱胎换骨的书
推荐语:卡内基梅隆大学计算机学院院长兼美国4大机构院士撰写,畅销6大洲40余国家,全球400余所高校核心教材,中文版累计销售30余万册。
考研数学在内容和难度上都更上一个等级,数学绝对是考研中最拉分的一门科目,从近十年真题来看,试卷中60%-80%的题目都是基础题目,基础知识扎实显得尤为重要。不论是数一、数二,还是数三,考研都涉及高等数学、线性代数、概率论。这几本被国内外数百所高校选作教材,畅销几十万册的数学教材给大家参考。
《概率论基础教程(原书第10版》

《概率论基础教程(原书第10版》
经过锤炼的优秀教材,已在世界范围内畅销三十多年
推荐语:经典概率论教材。通过大量的例子系统介绍了概率论的基础知识及其应用。
《线性代数(原书第10版)》

《线性代数(原书第10版)》
线性代数入门经典教材
推荐语:自1980年初版以来,畅销40多年,已经更新到第10版,中文版累计销售十几万册。
《线性代数及其应用》

《线性代数及其应用(原书第6版》
线性代数经典教材全新升级
推荐语:国内外数百所高校核心教材,中文版累计销售20余万册。线性代数应用典范,开创理论与实际应用相结合的先河。
当然啦,建议大家还是查看报考院校官方指定参考用书哦~先预祝大家,考研上岸!
重磅推荐:

赠书活动
根据博客阅读量本次活动一共赠书若干本,评论区抽取若干位小伙伴送出,中奖了会私信通知
参与方式:关注博主、点赞、收藏 + 评论
(任意评论不折叠即可,切记要点赞+收藏,否则抽奖无效,每个人最多评论三次)
活动截止时间:2023-09-26 17:00:00
原文链接:朋友圈大佬都去读研了,这份备考书单我码住了
相关文章:

【张兔兔送书第一期:考研必备书单】
考研书单必备 《数据结构与算法分析》《计算机网络:自顶向下方法》《现代操作系统》《深入理解计算机系统》《概率论基础教程(原书第10版》《线性代数(原书第10版)》《线性代数及其应用》赠书活动 八九月的朋友圈刮起了一股晒通知…...
基于Spring Boot+ Vue的健身房管理系统与实现
小熊学Java全能学面试指南:https://javaxiaobear.cn 摘要 随着健身行业的快速发展,健身房管理系统成为了提高管理效率和用户体验的重要工具。本论文旨在设计与实现一种基于前后端分离的健身房管理系统,通过前后端分离的架构模式,…...
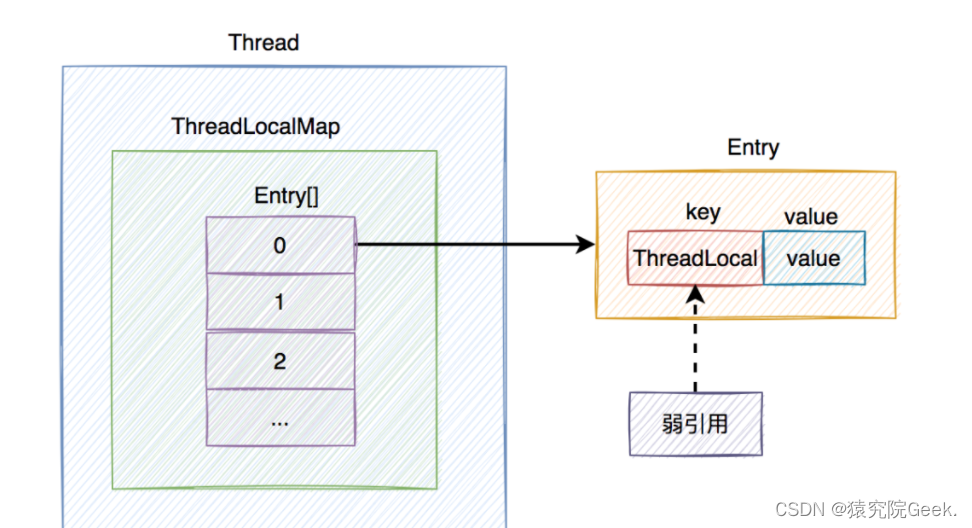
ThreadLocal线程局部变量
1.原理 ThreadLocal是用来保存当前线程数据的,每一个线程的内部都有一个ThreadLocalMap,当前这个map中存储了以当前ThreadLocal作键,具体的数据作值的一个个Entry对象。 为什么非得以ThreadLocal对象作键呢?因为一个线程可能使用了…...
C++ Primer (第五版)第一章习题部分答案
在我自学C过程中,我选择了CPrimer这本书,并对部分代码习题进行了求解以及运行结果。接下来几个月我将为大家定时按章节更新习题答案与运行结果: 目录 1.9编写程序,使用while循环将50到100的整数相加 1.10 除了运算符将运算对象的值增加1之外,还有一个…...

Python与GUI集成:零基础也能开发国际象棋游戏
引言: 国际象棋,作为世界上最受欢迎的棋类游戏之一,拥有丰富的策略和深度。但是,你知道自己可以使用Python来创建一个简单的国际象棋游戏并为其添加图形用户界面(GUI)吗?在本教程中,…...
SaaS软件能保证数据安全吗?
SaaS软件能保证数据安全吗? 本文将要尝试从各个方面尽可能客观的去阐述这个问题,而不是简单自嗨式的说简道云平台如何保障数据安全。 建议先收藏起来慢慢品! 01 SaaS安全到底是什么?——定义解读 本文所用SaaS平台>>>…...

方案:基于AI烟火识别与视频技术的秸秆焚烧智能化监控预警方案
一、方案背景 为严控秸秆露天焚烧,改善环境空气质量,各省相继发布秸秆禁烧工作内容。以安徽省为例,大气污染防治联席会议下发了该省2020年秸秆禁烧工作部署通知。2020年起,气象局将对全省秸秆焚烧火点实施卫星全年全时段监测&…...
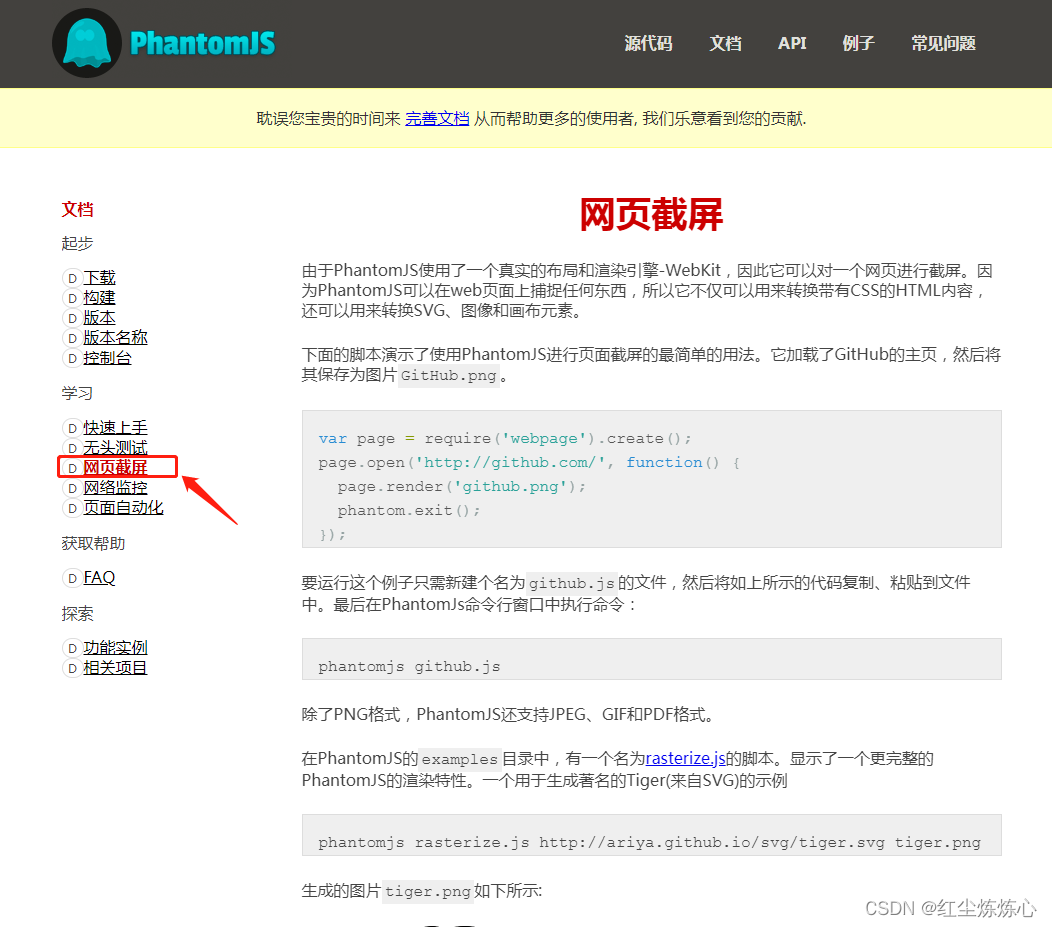
phantomjs插件---实现通过链接生成网页截图
Phantomjs | PhantomJS 配置要求 windows下,安装完成phantomJS 设置phantomjs环境变量【也可直接使用phantomjs目录下的执行文件】 直接通过访问php文件执行/通过cmd命令行执行【phantomjs phantom_script.js】 linux下,安装完成phantomJS 设置phantomjs环境变量 直…...
SpringBoot分页实现查询数据
1.原生查询 1.1创建分页查询实体类 package com.itheima.pojo;import lombok.AllArgsConstructor; import lombok.Data; import lombok.NoArgsConstructor;import java.util.List;//分页查询结果封装类 Data NoArgsConstructor AllArgsConstructor public class PageBean {pr…...
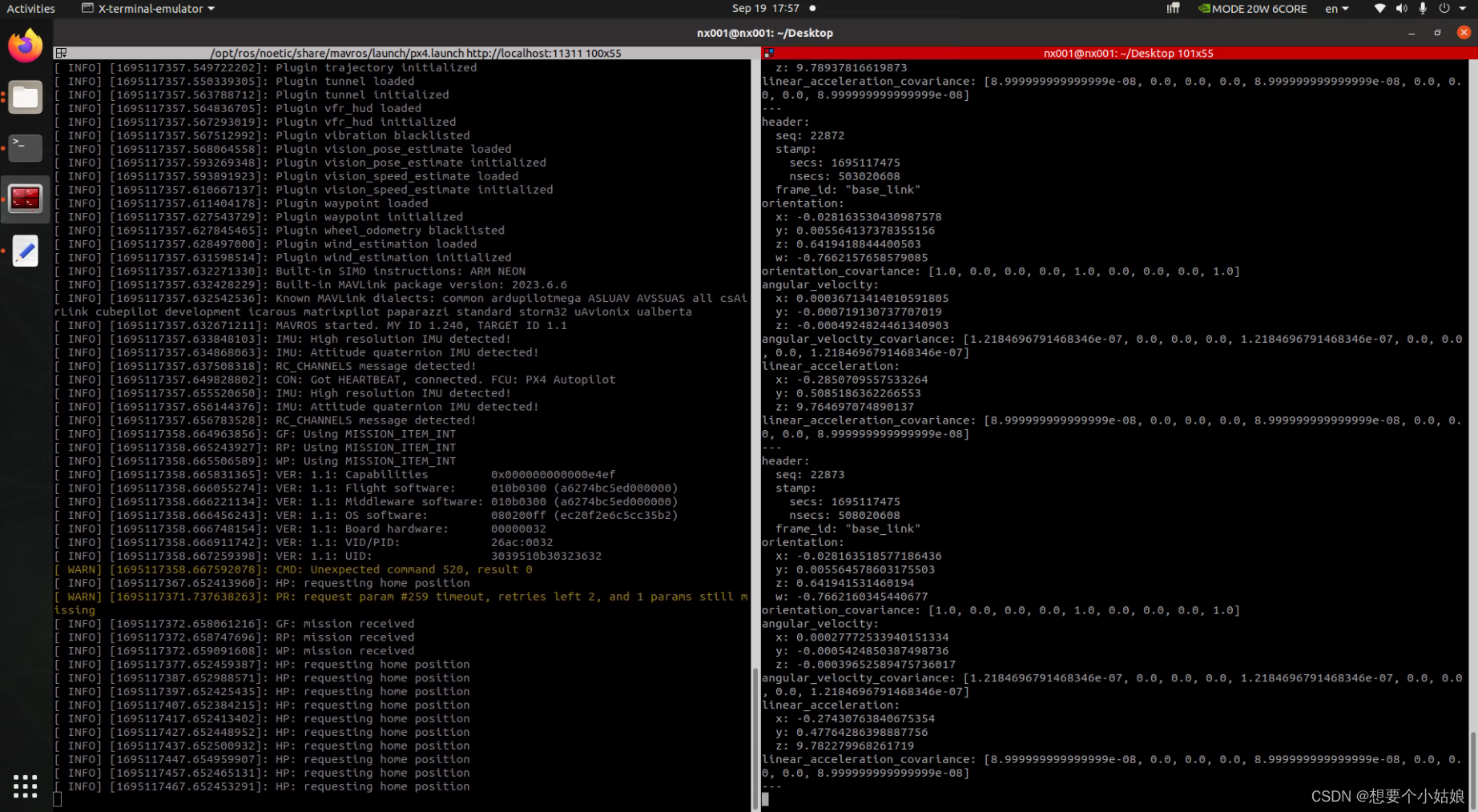
Jetson Xavier NX 与飞控(Pixhawk 4 Mini)实现串口通信
一、飞控端配置 首先对 Pixhawk 4 Mini 烧录固件参考 Kakute H7 刷写 px4 固件_想要个小姑娘的博客-CSDN博客 烧录完成后打开 QGroundControl,进入参数设置并搜索 MAV,如下所示 然后修改 MAV_1_CONFIG,修改为自己想要连接机载电脑…...
为什么2022年秋招嵌入式开发岗位薪资大涨?
今天看到一个网友讨论的问题,其实这个问题也很简答。从嵌入式本身优势来说,首先是因为该行业人才人才需求大,据权威统计机构统计在所有软件开发类人才的需求中,对嵌入式工程师的需求达到全部需求量的60%~80%,并且每年以…...

在HTML里,attribute和property有什么区别?
在HTML中,attribute 和 property 之间的区别是一个常见但容易混淆的概念。它们都与HTML元素有关,但它们在功能、用途和行为上有所不同。以下是它们之间的主要区别: 定义和来源: Attribute: 它们是在HTML标记中定义的,通常用于提供…...

机器学习入门与实践:从原理到代码
💂 个人网站:【工具大全】【游戏大全】【神级源码资源网】🤟 前端学习课程:👉【28个案例趣学前端】【400个JS面试题】💅 寻找学习交流、摸鱼划水的小伙伴,请点击【摸鱼学习交流群】 在本文中,我…...
SpringCloud在idea中一键启动项目
1、如下图文件中加上: <component name"RunDashboard"><option name"configurationTypes"><set><option value"SpringBootApplicationConfigurationType" /></set></option></component>…...

VB过程的递归调用,辗转相除法求最大公约数
VB过程的递归调用,辗转相除法求最大公约数 过程的递归调用,辗转相除法求最大公约数 Private Function gys(ByVal m%, ByVal n%) As IntegerDim r%r m Mod n m大或者n大都无所谓,这个不影响计算,由于辗转相除法的算法,…...

OpenCV(三十九):积分图像
1.积分图像介绍 积分图像中的每个像素表示了原始图像中对应位置及其左上方矩形区域内像素值的总和。如图,p0表示原始图像蓝色区域内像素值的总和。 倾斜求和(Skewed Sum)是积分图像的一种扩展形式,用于计算图像区域内的像素和&…...

【Electron 拦截请求实现自定义网络处理】
文章目录 Electron 拦截请求实现自定义网络处理1. 获取默认会话2. 拦截请求3. 完整示例代码总结 Electron 拦截请求实现自定义网络处理 在 Electron 中,我们可以使用 session 模块来拦截和处理网络请求。通过拦截请求,我们可以对请求进行修改、添加请求…...

Pytest系列-内置标签skip和skipif 跳过测试用例的详细使用(5)
简介 skip和skipif,见名知意就是跳过测试,主要用于不想执行的代码,标记后,标记的代码不执行。希望满足某些条件才执行某些测试用例,否则pytest会跳过运行该测试用例实际常见场景:根据平台不同执行测试、跳…...
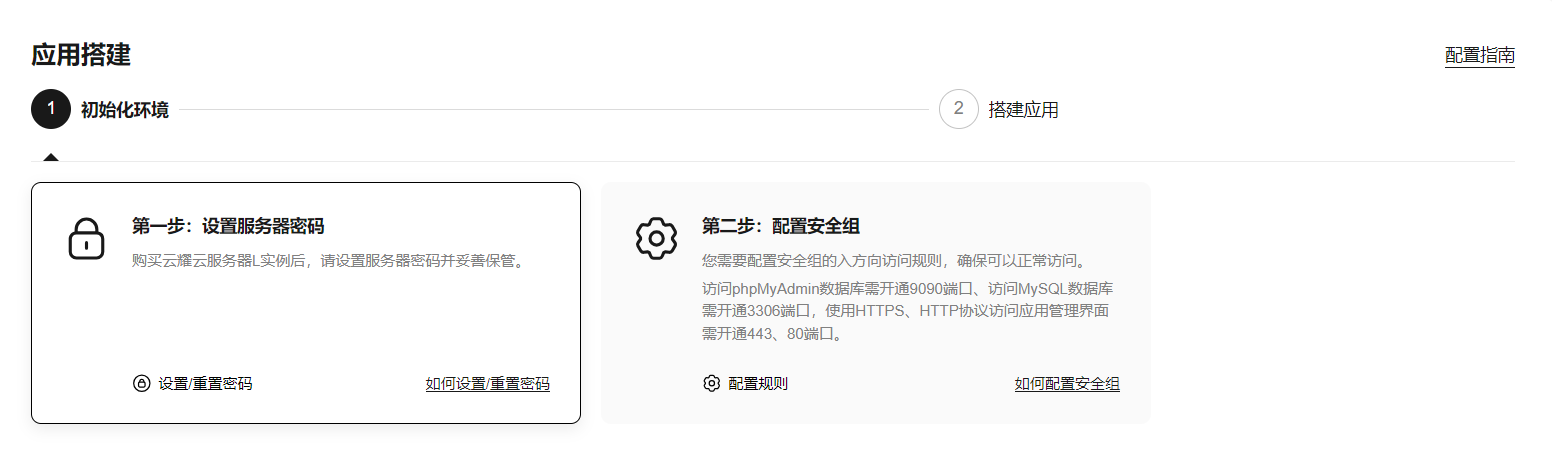
华为云云耀云服务器L实例评测|docker 常用操作命令
文章目录 写在前面云耀云服务器L实例与ECS的购买和配置区别 1、管理命令2、帮助命令3、镜像命令4、容器命令4.1 查看容器4.2 创建容器 实例 写在前面 前面讲到了docker环境的安装,这是我们可以直接打开远程连接华为云云耀云服务器L实例,直接连接公网…...

RJ45网络信号浪涌保护器解决方案
RJ45网络信号浪涌保护器是一种用于保护网络设备免受雷击或其他高压电流干扰的装置,它可以有效地吸收和释放信号线路上的过电压,从而避免设备损坏或数据丢失。 RJ45信号浪涌保护器的应用领域和施工方案如下: 地凯科技RJ45网络信号浪涌保护器…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
