当前位置： 首页 > news >正文

CAN - 基础

news 2026/2/9 2:10:39

CAN 基础

  • 概念
    • 分类
    • 特点
    • 物理层
      • 收发器
      • 线与
      • 编码方式
      • 通信方式
        • 采样点/位
      • 常见故障
    • 数据链路层
      • CAN控制器
      • 数据帧
        • 分类
        • 数据帧格式
        • 数据帧DBC解析
        • CRC校验
        • 远程帧
      • 总线竞争与仲裁
        • 非破坏性仲裁机制
      • 节点状态与错误处理机制
        • 节点状态
        • 错误处理机制
        • 错误帧

概念

分类

  • CAN
  • CAN FD
  • 高速CAN
  • 低俗容错CAN

特点

  • 多主通讯 （节点之间 一对一、一对多、多对一、广播等）
  • 短帧结构：报文帧的有效字节有8个
  • 报文ID值越小，优先级越高
  • 非破坏性总线仲裁处理机制
  • 可靠的CRC校验方式，传输数据出错率极低
  • 在报文帧仲裁失败或传输期间被破坏有自动重发机制
  • 节点在错误严重的情况下，具有自动脱离总线的功能，切断它与总线的联系，不影响总线的正常工作

物理层

收发器

数字信号 <–> 物理信号（CAN_H/CAN_L）两者之间的转换采用差分电平信号
属于OSI模型中的物理层

线与

多个CAN节点并介到同一总线时，只要其中一个节点输出低电平，总线就为低电平
当所有节点输出高电平，总线才为高电平

编码方式

通信方式

异步串行通信：采样点按约定的频率采样数据，根据波特率采样

为减少波特率的误差带来的通信错误
解决：CAN总线规定信号的跳变沿时刻进行同步，将误差累积限制在两个跳变沿
问题：发送多个相同位时没有跳变沿用于同步，会导致误差不断累计
解决：使用位填充的方法进行同步：采用填充位在连续5个相同位后插入一个相反位，产生跳变沿，用于同步（这里时CAN控制器自己去填充）

采样点/位

一个位时间=1/波特率
位时间：同步段、传播段、相位缓冲段1、相位缓冲段2
1位时间=10时间份额

  • 同步段：1时间份额
  • 传播段：1时间份额
  • 相位缓冲段1：4时间份额
  • 相位缓冲段2：4时间份额
    一个时间份额：Tq
    采样点：规定在第x个时间份额后进行采样

常见故障

数据链路层

CAN控制器

属于OSI模型中的数据链路层

数据帧

分类

  • 数据帧

发送节点向接收节点传送数据，使用最多

  • 远程帧

接收节点向某个发送节点请求数据（发送节点让另外一个节点反馈数据的时候）

  • 错误帧

当总线、某节点检测出错误时向其他节点通知错误的帧

  • 过载帧

接收节点向发送节点通知自身接收能力的帧

  • 间隔帧

数据帧或远程帧与前面的帧分离的帧

数据帧格式

-

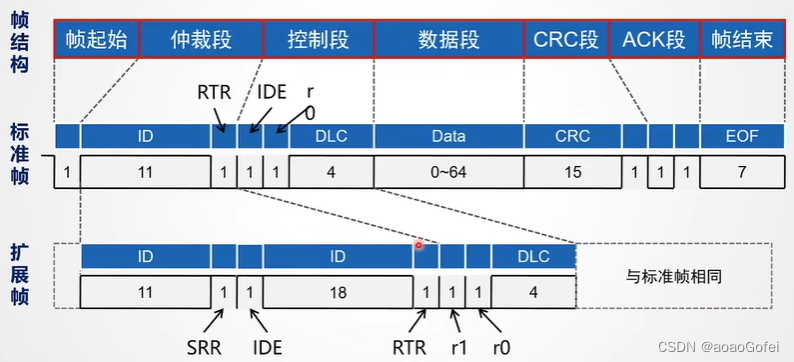
格式

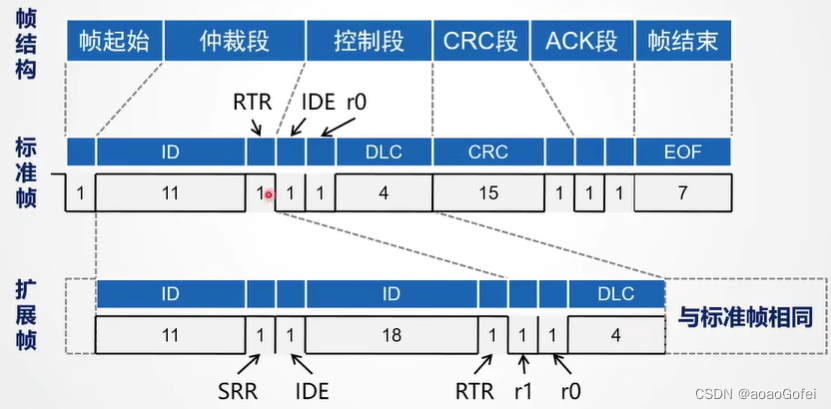
  • 帧起始(1位)：显性位SOF，标识一个数据帧的开始，用于同步；只有在总线空闲期间，节点才能发送SOF（在总线空闲的时候，发送节点发出帧起始；其他接收节点从这个帧起始位进行同步（用于减少累计误差））

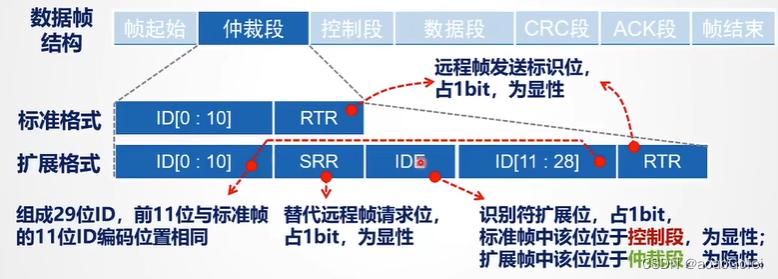
在这里插入图片描述

  • ID(11位)：标识符，唯一确定一条报文，表明报文的含义，可以包括报文的源地址、目标地址；用于确定报文的仲裁优先级（ID数值越小，优先级越高）
  • SRR(1位)：无实际意义，SRR永远置1
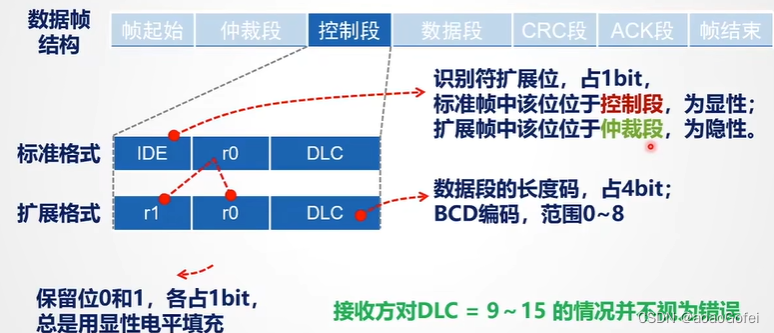
  • IDE(1位)：用于区分标准帧和扩展帧：标准帧IDE=0（11位ID）;扩展帧IDE=1（29位ID）
  • extended ID（18位）：如果IDE=1
  • RTR位(1位)：区分数据帧和远程帧（没有数据场？？？很少用）：数据帧RTR=0; 远程帧RTR=1

在这里插入图片描述

  • r1(1位)：保留位，显性电平0填充

  • r0(1位)：保留位，显性电平0填充

  • DLC(4位)：数据场包含数据的字节数
    在这里插入图片描述

  • 数据场(0-8个字节)：实际CAN数据发送的内容

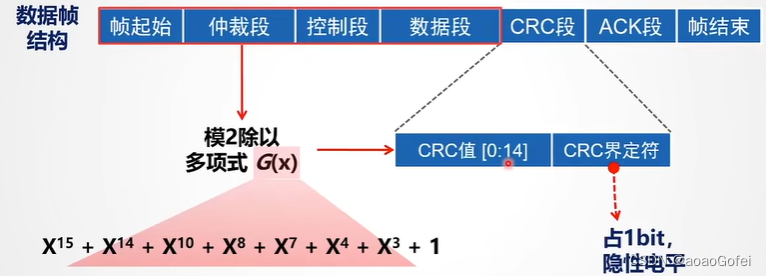
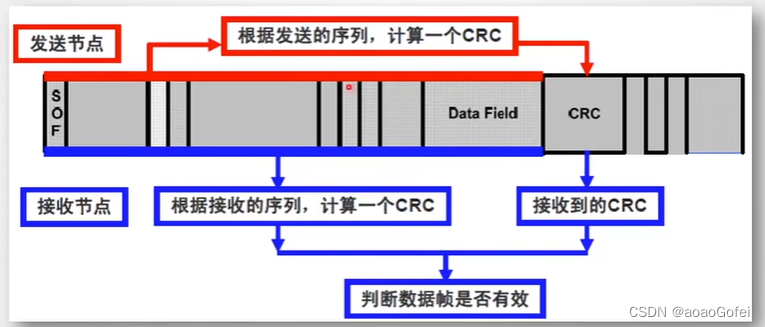
在这里插入图片描述

  • CRC（15位）：进行CRC校验，CRC位之前的所有数据位根据一定规则进行校验

  • DEL(1位)：CRC界定符，在CRC界定符之前 从SOF开始，到DEL之前进行位填充，显性位电平0
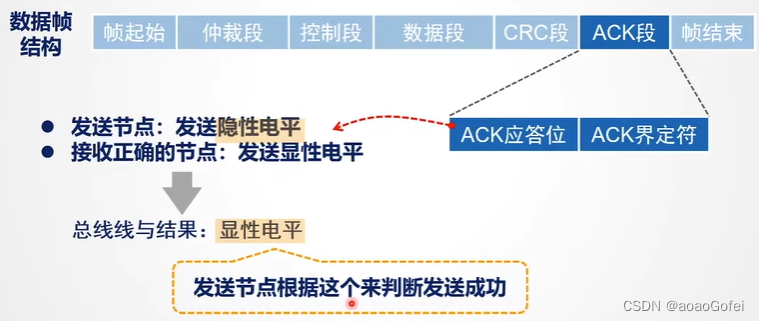
    在这里插入图片描述

  • ACK(1位): 确定报文被至少一个节点正确接收（发送节点ACK置1（隐性电平），接受方正确接收报文，则将ACK位置0（显性电平）），发送节点查看ACK位从以隐性变显性，知道有节点接收数据，如果没有节点接收，则报相应的错误帧

  • DEL(1位)：界定符，隐性位电平1

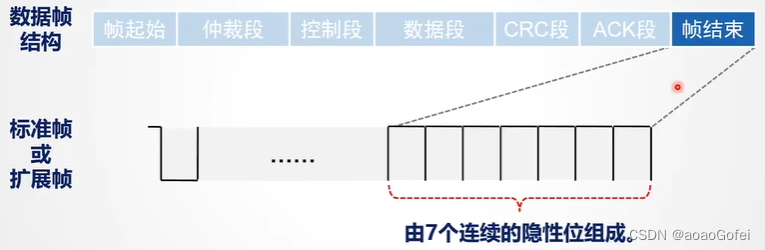
在这里插入图片描述

  • EOF(7位)：连续7个隐性位
  • ITM(3位)：连续3个隐性位
  • ITM之后，总线会进入空闲状态，此时其他节点可以发送报文，如果节点检测到11个连续的隐性位，就认为总线进入空闲阶段（1+7+3）

数据帧DBC解析

CRC校验

在这里插入图片描述

远程帧

  • 标准帧
  • 扩展帧

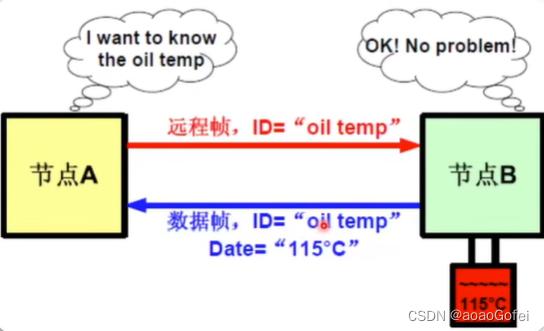
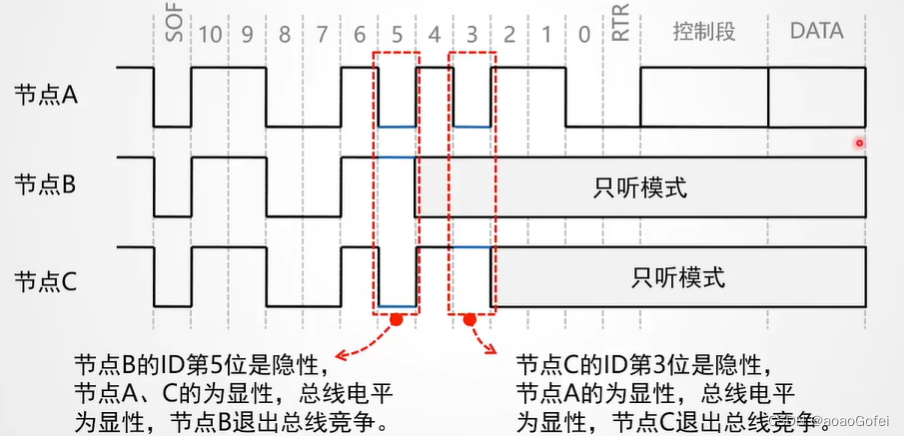
在这里插入图片描述
在这里插入图片描述

总线竞争与仲裁

竞争：多个节点同时要发送数据

非破坏性仲裁机制

仲裁发生在仲裁段
采用“线与”机制
ID值越小，优先级越高
仲裁失败进入“只听”模式

在这里插入图片描述

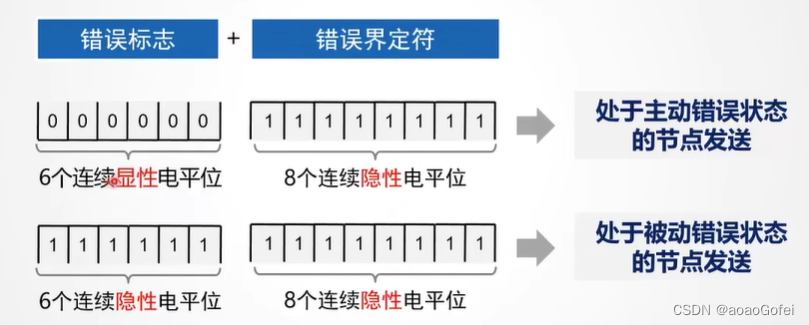
节点状态与错误处理机制

节点状态

  • 主动错误状态

设备正常参与总线通信，检测到错误时发送主动错误标识

  • 被动错误状态

设备正常参与总线通信，检测到错误时发送主动错误标识

  • 总线关闭

数据帧的收发被禁止，脱离总线

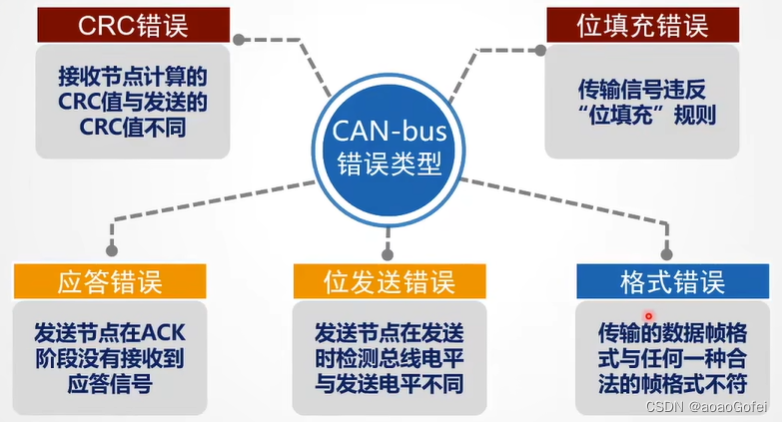
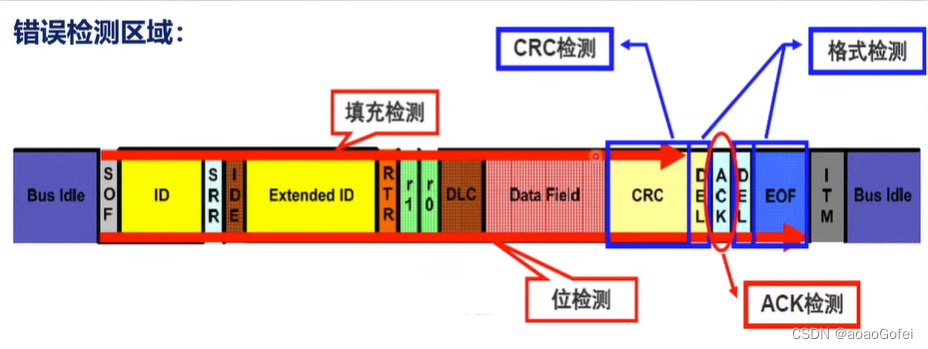
在这里插入图片描述
在这里插入图片描述

错误处理机制

  • CRC 错误
  • 位填充错误
  • 应答错误
  • 位发送错误
  • 格式错误

在这里插入图片描述
在这里插入图片描述

错误帧

在这里插入图片描述

相关文章：

CAN - 基础

CAN 基础 概念分类特点物理层收发器线与编码方式通信方式采样点/位 常见故障 数据链路层CAN控制器数据帧分类数据帧格式数据帧DBC解析CRC校验远程帧 总线竞争与仲裁非破坏性仲裁机制 节点状态与错误处理机制节点状态错误处理机制错误帧 概念 分类 CANCAN FD高速CAN低俗容错CA…...

编程日记 2023/9/20 14:36:36

【Hash表】找出出现一次的数字-力扣 136

&#x1f49d;&#x1f49d;&#x1f49d;欢迎来到我的博客&#xff0c;很高兴能够在这里和您见面&#xff01;希望您在这里可以感受到一份轻松愉快的氛围&#xff0c;不仅可以获得有趣的内容和知识&#xff0c;也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学…...

编程日记 2023/9/20 14:32:32

Resize和centerCrop的区别

首先要记住,transforms只能对PIL读入的图片进行操作,而且PIL和opencv只能读取H * W * C形式的图片。 resize(size)&#xff1a;将图片的短边缩放成size的比例&#xff0c;然后长边也跟着缩放&#xff0c;使得缩放后的图片相对于原图的长宽比不变。如果想要resize成自己想要的图…...

编程日记 2023/9/20 14:29:29

无涯教程-JavaScript - SUM函数

描述 SUM函数可添加值。 语法 SUM (number1, [number2]...)争论 Argument描述Required/Optionalnumber1The first number you want to add. The number can be a value, a cell reference, or a cell range.Requirednumber2, …You can specify up to 255 additional numbe…...

编程日记 2023/9/20 14:28:28

ChatGLM P-Tuningv2微调定制AI大模型

前言 什么是模型微调 想象一下，你正在学习如何弹奏一首钢琴曲目。你已经学会了一些基本的钢琴技巧，但你想要更进一步，尝试演奏一首特定的曲目。这时，你会选择一首你感兴趣的曲目，并开始深度练习。 Fine-tuning（微调）在机器学习中也是类似的概念。当我们使用预先训练好…...

编程日记 2023/9/20 14:25:24

关于RISC-V安全性的全面综述

目录 摘要引言RISC-V安全综述通用平台的安全要求信任的根源与硬件安全模块OTP管理模块安全内存对称加密&#xff08;如AES&#xff09;引擎不对称加密[131]&#xff08;例如&#xff0c;公钥RSA&#xff09;引擎HASH/HAMC引擎随机数/位生成&#xff08;例如TRNG[136]&#xff0…...

编程日记 2023/9/20 14:22:22

Python基础语法规则和Java不同的地方

Java是现在最流行的语言&#xff0c;也是广大程序员最熟悉的语言。然而&#xff0c;随着人工智能领域的快速发展&#xff0c;Python作为新星崭露头角。通过对比Java语言来学习Python语言&#xff0c;可以事半功倍。 首先&#xff0c;我们来看Python和Java在注释上的区别。在Jav…...

编程日记 2023/9/20 14:21:19

振弦采集仪安全监测路基边坡的解决方案

振弦采集仪安全监测路基边坡的解决方案 随着人们对交通安全的重视和公路工程的发展&#xff0c;路基边坡安全监测成为了重要的课题之一。路基边坡作为公路的基础&#xff0c;其稳定性直接关系到公路的使用寿命和行车安全。而振弦采集仪作为一种新型的安全监测设备&#xff0c;可…...

编程日记 2023/9/20 14:18:16

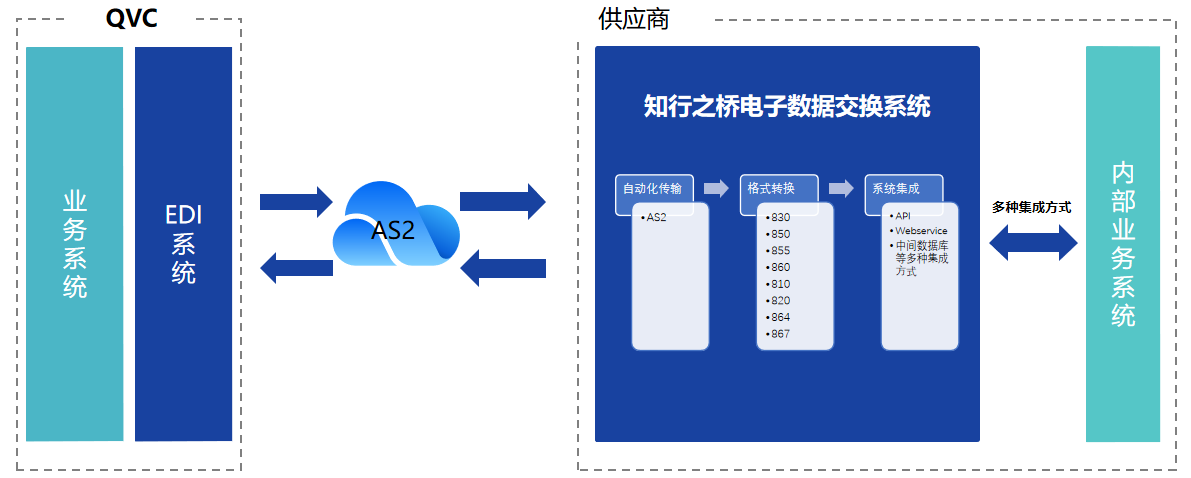
如何与QVC 建立EDI连接？

QVC&#xff0c;全称为Quality, Value, Convenience&#xff08;品质、价值、便利&#xff09;&#xff0c;成立于1986年&#xff0c;是一家全球领先的零售电视和在线零售商。作为一家多渠道零售商&#xff0c;QVC致力于为客户提供高品质、独特的商品&#xff0c;通过电视、互联…...

编程日记 2023/9/20 14:16:13

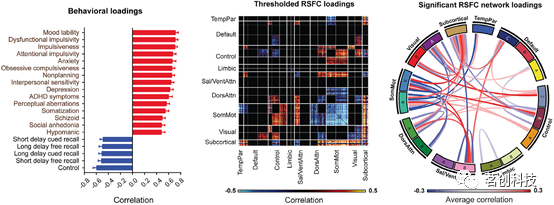
脑网络图谱

前言 研究人脑面临的一个挑战是其多尺度组织和系统复杂性。我们对大脑组织的认识主要来源于离体组织学检查&#xff0c;如细胞结构映射。通过研究全脑微观结构特征的变化&#xff0c;可以划分为不同的脑区。然而&#xff0c;这种研究大脑组织的“局部”方法非常耗时、耗资源&a…...

编程日记 2023/9/20 14:12:09

无涯教程-JavaScript - SQRTPI函数

描述 SQRTPI函数返回(number * pi)的平方根。 语法 SQRTPI (number)争论 Argument描述Required/OptionalNumberThe number by which pi is multiplied.Required Notes If the specified number < 0, SQRTPI returns the #NUM! error value.如果指定的数字为非数字,则S…...

编程日记 2023/9/20 14:10:07

Nacos使用教程（四）——命名空间（Namespace）、配置分组（Group）和配置集ID（Data ID）

文章目录 Nacos命名空间&#xff08;Namespace&#xff09;一、什么是命名空间二、命名空间的作用1. 隔离环境2. 分类管理3. 权限控制 三、命名空间的使用四、总结 Nacos配置分组&#xff08;Group&#xff09;一、什么是配置分组二、配置分组的作用1. 分类管理2. 隔离控制3. 动…...

编程日记 2023/9/20 14:09:05

三、双指针（two-point）

文章目录 一、算法核心思想二、算法模型&#xff08;一&#xff09;对撞指针1.[704.二分查找](https://leetcode.cn/problems/binary-search/)&#xff08;1&#xff09;思路&#xff08;2&#xff09;代码&#xff08;3&#xff09;复杂度分析 2.[15.三数之和](https://leetco…...

编程日记 2023/9/20 14:08:04

Redis 是什么和使用场景概述（技术选型）

一、Redis 是什么 Redis是一款开源的高性能键值存储系统。它支持多种数据结构&#xff0c;如字符串、列表、集合、哈希表、有序集合等&#xff0c;并提供了丰富的操作命令和功能。Redis的主要特点包括&#xff1a; 内存存储&#xff1a;Redis将数据存储在内存中&#xff0c;因此…...

编程日记 2023/9/20 14:07:03

【数据结构】七大排序

文章目录 &#x1f490;1. 插入排序&#x1f33c;1.1 直接插入排序&#x1f33c;1.2 希尔排序 &#x1f490;2. 选择排序&#x1f33c;2.1 直接选择排序&#x1f33c;2.2 堆排序 &#x1f490;3. 交换排序&#x1f33c;3.1 冒泡排序&#x1f33c;3.2 快速排序&#x1f33c;3.2.…...

编程日记 2023/9/20 14:05:00

区块链实验室(24) - FISCO网络重构

若干次实验以后&#xff0c;FISCO网络中100个节点堆积了不少交易记录&#xff0c;消耗不少磁盘空间&#xff0c;见下图所示&#xff0c;100个节点累计消耗了10G空间。 观察每个节点的磁盘消耗&#xff0c;以node88为例&#xff0c;消耗了107MB&#xff0c;见下图所示。在该节点…...

编程日记 2023/9/20 14:03:59

AI智能写作工具有哪些？永久免费的AI智能写作工具你使用过吗？

AI智能写作是指借助人工智能技术&#xff0c;计算机程序可以自动生成各种文本内容&#xff0c;包括新闻报道、广告文案、科技文章、小说等等。这些AI写作工具通过大数据和深度学习模型&#xff0c;能够分析和模仿人类的写作风格&#xff0c;生成高质量的文本&#xff0c;甚至有…...

编程日记 2023/9/20 14:02:58

23.8.15 杭电暑期多校9部分题解

1002 - Shortest path 题目大意 对于一个数 x x x&#xff0c;可以进行以下三种操作&#xff1a; 1.将 x x x 变成 2 ∗ x 2*x 2∗x 2.将 x x x 变成 3 ∗ x 3*x 3∗x 3.将 x x x 变成 x 1 x1 x1 给定一个数 n n n&#xff0c;问最少操作几次才能将 1 1 1 变成…...

编程日记 2023/9/20 14:01:57

四个BY的区别 HIVE中

在Hive中&#xff0c;有四个BY比较&#xff1a;Order By、Sort By、Distribute By和Cluster By。 Order By是全局排序&#xff0c;只有一个Reducer。它可以按照升序&#xff08;ASC&#xff09;或降序&#xff08;DESC&#xff09;对结果进行排序。Order By子句通常用在SELECT语…...

编程日记 2023/9/20 13:59:53

计时函数与float32 float16 int8 数据转换

个人整理常用 部分来自 ncnn 计时函数 // window 平台 #include <windows.h>double get_current_time() {LARGE_INTEGER freq; // 频率LARGE_INTEGER pc; // 计数QueryPerformanceFrequency(&freq);QueryPerformanceCounter(&pc);return pc.QuadPart * 1000…...

编程日记 2023/9/20 13:56:50

【大模型RAG】拍照搜题技术架构速览：三层管道、两级检索、兜底大模型

摘要 拍照搜题系统采用“三层管道&#xff08;多模态 OCR → 语义检索 → 答案渲染&#xff09;、两级检索&#xff08;倒排 BM25 向量 HNSW&#xff09;并以大语言模型兜底”的整体框架&#xff1a; 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后&#xff0c;分别用…...

编程新知 2026/2/8 4:32:38

Flask RESTful 示例

目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题&#xff1a; 下面创建一个简单的Flask RESTful API示例。首先&#xff0c;我们需要创建环境&#xff0c;安装必要的依赖&#xff0c;然后…...

编程新知 2026/2/8 20:42:43

多场景 OkHttpClient 管理器 - Android 网络通信解决方案

下面是一个完整的 Android 实现&#xff0c;展示如何创建和管理多个 OkHttpClient 实例&#xff0c;分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

编程新知 2025/12/15 1:34:37

深入浅出：JavaScript 中的 `window.crypto.getRandomValues()` 方法

深入浅出&#xff1a;JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中&#xff0c;随机数的生成看似简单&#xff0c;却隐藏着许多玄机。无论是生成密码、加密密钥&#xff0c;还是创建安全令牌&#xff0c;随机数的质量直接关系到系统的安全性。Jav…...

编程新知 2025/10/8 4:56:09

iPhone密码忘记了办？iPhoneUnlocker，iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版​分享

平时用 iPhone 的时候&#xff0c;难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵&#xff0c;或者买了二手 iPhone 却被原来的 iCloud 账号锁住&#xff0c;这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

编程新知 2026/1/29 10:22:28

工程地质软件市场：发展现状、趋势与策略建议

一、引言 在工程建设领域&#xff0c;准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具&#xff0c;正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

编程新知 2025/10/6 6:10:29

html-＜abbr＞ 缩写或首字母缩略词

定义与作用 <abbr> 标签用于表示缩写或首字母缩略词&#xff0c;它可以帮助用户更好地理解缩写的含义&#xff0c;尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时&#xff0c;会显示一个提示框。 示例&#x…...

编程新知 2026/1/24 19:22:03

rnn判断string中第一次出现a的下标

# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

编程新知 2025/9/24 16:25:00

学习一下用鸿蒙​​DevEco Studio HarmonyOS5实现百度地图

在鸿蒙&#xff08;HarmonyOS5&#xff09;中集成百度地图&#xff0c;可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API&#xff0c;可以构建跨设备的定位、导航和地图展示功能。 ​​1. 鸿蒙环境准备​​ ​​开发工具​​&#xff1a;下载安装 ​​De…...

编程新知 2025/11/13 2:37:01

SQL Server 触发器调用存储过程实现发送 HTTP 请求

文章目录 需求分析解决第 1 步：前置条件，启用 OLE 自动化方式 1：使用 SQL 实现启用 OLE 自动化方式 2：Sql Server 2005启动OLE自动化方式 3：Sql Server 2008启动OLE自动化第 2 步：创建存储过程第 3 步：创建触发器扩展 - 如何调试？第 1 步：登录 SQL Server 2008第 2 步…...

编程新知 2025/9/11 6:56:11