典型数据结构-栈/队列/链表、哈希查找、二叉树(BT)、线索二叉树、二叉排序树(BST树)、平衡二叉树(AVL树)、红黑树(RB树)
目录
典型数据结构列举
栈/队列/链表
树
二叉树
线索二叉树
二叉排序树
平衡二叉树(AVL树)
红黑树
其它树种和应用介绍
典型数据结构列举
栈/队列/链表
描述略。
一些基本的简单实现参考/数据结构简单实现/文件夹里面。
- 线性表详解:数据结构线性表10分钟入门 (biancheng.net)。
- 栈(Stack)和队列(Queue)详解 (biancheng.net)。
树
以下为树的基本概念(定义、基本操作、性质、存储结构等)、二叉树(定义、基本操作、存储、遍历等)、平衡二叉树、红黑树等。
引自:树及二叉树的基本概念_青萍之末的博客-CSDN博客。
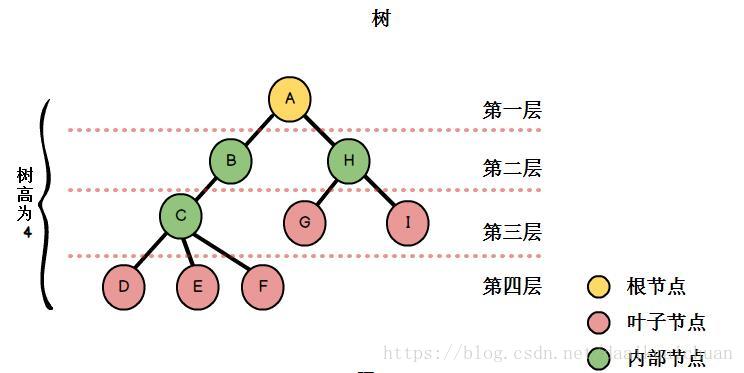
树是由一个或一个以上的节点(node)组成,存在一个特殊节点称为树根(root),它是n(n>=0)个节点的有限集。n=0时称为空树。n>0时,有限集的元素构成一个具有层次感的数据结构。
树的一些概念
- 节点的度:一个节点拥有子树的数目。例如A的度为2,B的度为1,C的度为3。
- 树的高度:也称为树的深度,树中节点的最大层次。
- 有序树:树中节点各子树之间的次序是重要的,不可以随意交换位置。
- 无序树:树种节点各子树之间的次序是不重要的。可以随意交换位置。
- 森林:0或多棵互不相交的树的集合。
引自:《数据结构教程》。
树的一些性质
- 非空树的节点总数等于树中所有节点的度之和加1。
- 度为 k 的非空树的第 i 层,最多有 k^(i-1) 个节点(i ≥ 1)。
- 深度为 h 的 k 叉树最多有 (k^h - 1)/(k - 1) 个节点。
- 具有 n 个节点的 k 叉树的最小深度为 log_k(n*(k - 1)) + 1。包含 n 个结点的二叉树的高度至少为 log_2(n) + 1。
树的基本操作
- 建立一棵空树 T。
- 求结点 x 所在树的根节点。或求树 T 的根节点。
- 求树 T 中结点 x 的双亲结点。
- 求树 T 中节点 x 的第 i 个孩子节点。
- 求树 T 中节点 x 右边 的兄弟节点。
- 把以 S 为根结点的树插入到 树 T 的 节点 x 的第 i 个子节点位置上。
- 删除树 T 中 节点 x 的第 i 棵树。
- 对一棵树进行遍历,按照某种次序遍历树所有节点并得到一个由所有节点组成的序列。
树的存储
采用链式存储方式居多。除了储存节点本身的数据信息之外,还必须做到把树中各个节点之间的连接关系反映在存储结构中。
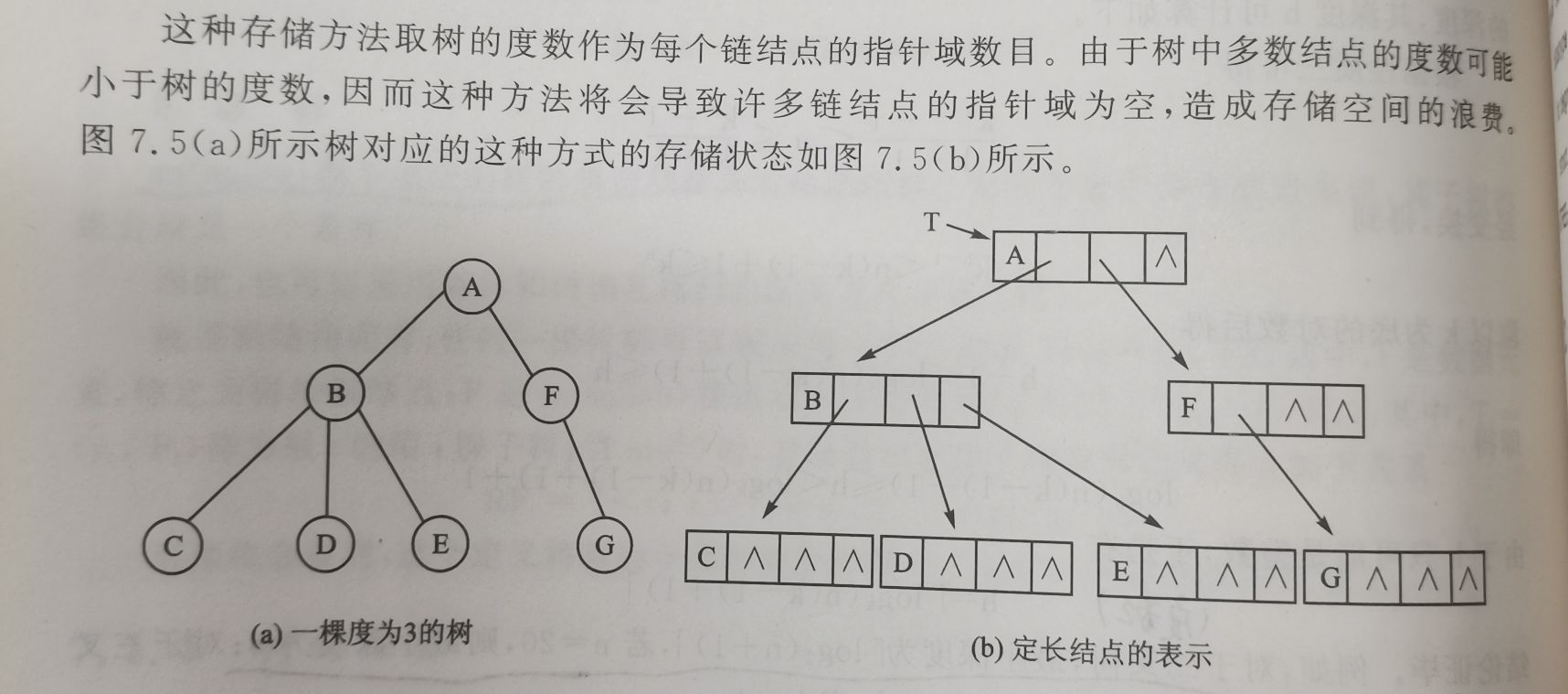
多重链表表示法:分为 定长链接数目 和 不定长链接数目。
前者:
后者:
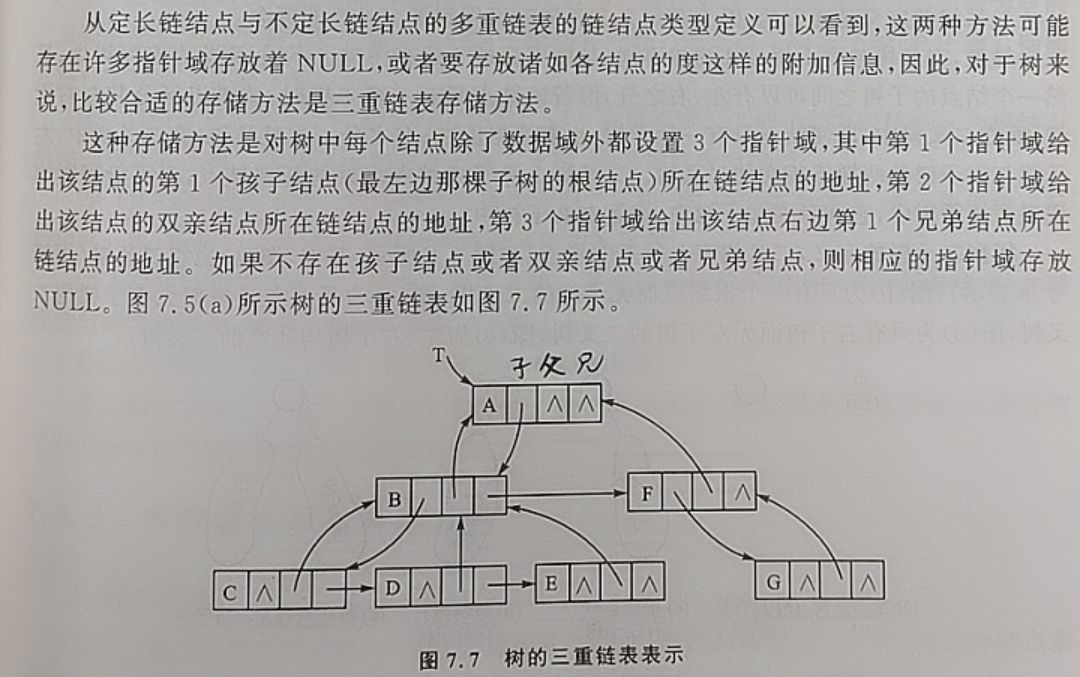
三重链表表示法:
二叉树
树及二叉树的基本概念_青萍之末的博客-CSDN博客。
引自:《数据结构教程》。
二叉树结构被广泛用来解决计算机领域中的各种实际问题。例如,在排序、检索、数据库管理系统以及人工智能等许多方面,二叉树都提供了强而有效的支持。
…
每一个节点最多只有两颗子树。在二叉树中严格区分节点的左、右子树,其次序不能随意颠倒。因此二叉树是有序树。
二叉树又可以分为满二叉树和完全二叉树。
二叉树的基本操作
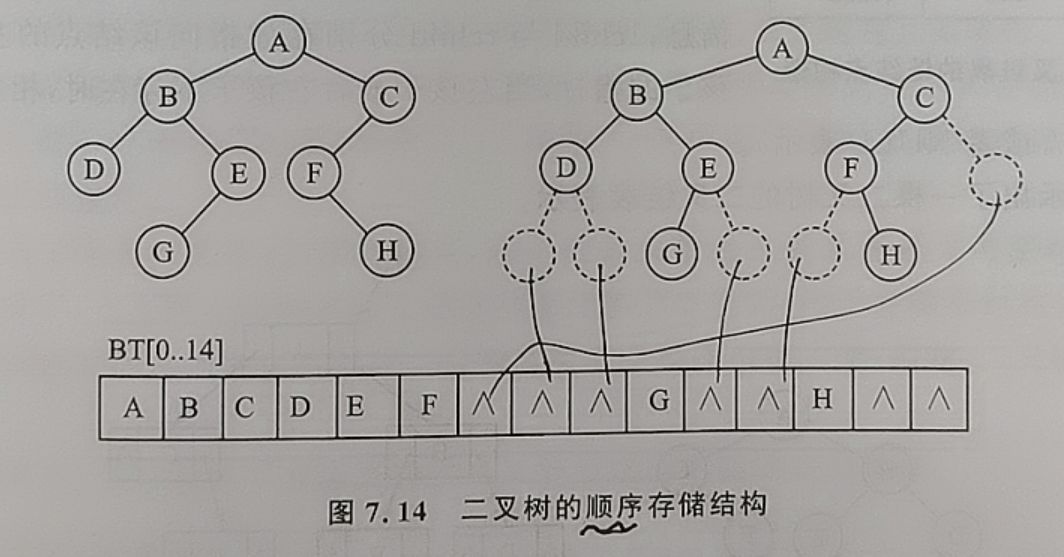
二叉树的存储结构
顺序存储结构:顺序存储结构固有一些缺陷,使得二叉树的插入、删除等操作不方便,而且效率比较低(线性表的固有缺点)。
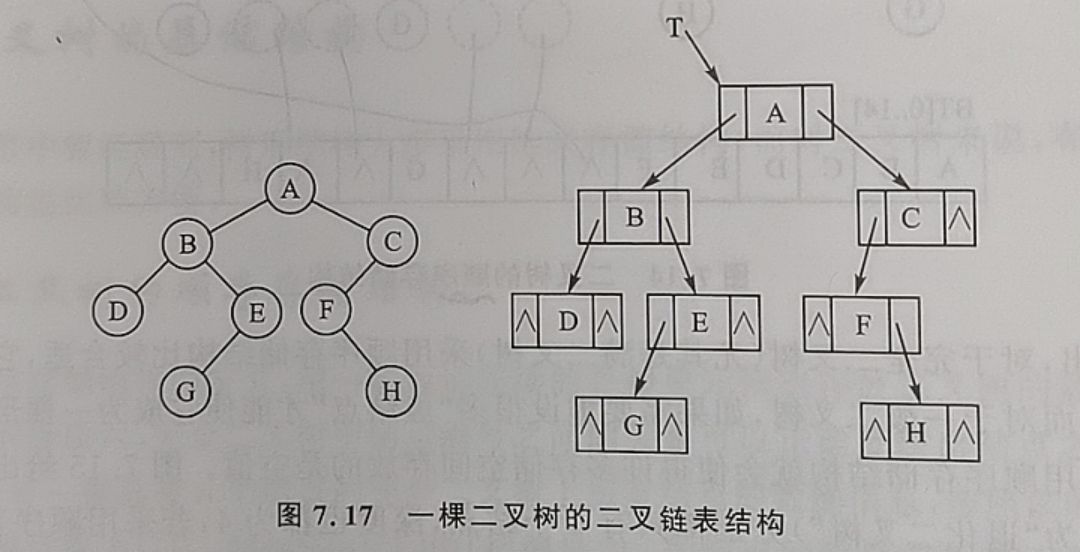
链式存储结构:更适合,更广泛。两种:二叉链表结构 和 三叉链表结构。
二叉链表结构:链表中每一个链接点由三个域组成分,别为数据域和两个指针域,后者分别给出该节点的左、右节点的存储地址。
三叉链表结构:相比于二叉链表结构,多增加一个用来指向双亲节点的指针域,这样在查找二叉树中某个节点的双亲节点时候不用遍历整个二叉树。就是空间换时间(如查找的时间等)。
二叉树与树的遍历
有关二叉树的许多操作几乎都是建立在二叉树的遍历之上。二叉树是一种非线性结构,因此需要寻找一种规律,使得二叉树中的所有节点能够排列在一个线性序列中,这就叫遍历。
若以符号 D、L 和 R 分别表示访问根节点、遍历根结点的左子树 和 遍历根结点的右子树 三个过程,并且限定先左后右的顺序,则通常采用三种遍历方式:DLR、LDR、LRD,分别称之为 前序遍历、中序遍历、后续遍历。还有 按层次 的遍历顺序。
遍历可以用递归的方式(对于很大的树容易栈溢出)。非递归方法,通常利用一个栈结构。
下面举例按照 中序遍历 顺序遍历的程序。
按照层次遍历(或叫 广度优先遍历) 即 若被遍历的二叉树非空,则依次访问二叉树的第1层、第2层……直到最后一层,对每一层的访问按照从左到右的顺序进行。 该方法通常用一个队列实现。下面举例程序。
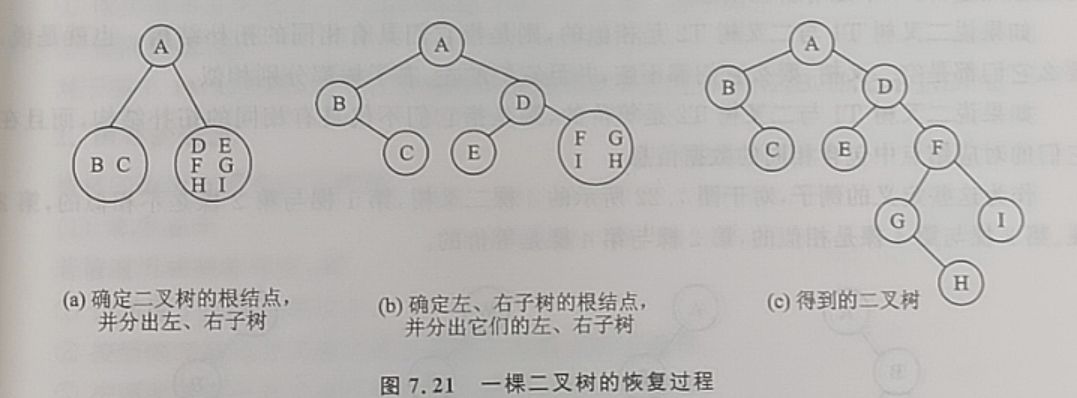
由遍历序列恢复二叉树
三步:
线索二叉树
在二叉树的结点上加上线索的二叉树称为线索二叉树。对于n个结点的二叉树,在二叉链存储结构中有n+1个空链域,利用这些空链域存放在某种遍历次序下该结点的前驱结点和后继结点的指针,这些指针称为线索,加上线索的二叉树称为线索二叉树。
- 彻底理解线索二叉树_ Walk the horizon-CSDN博客 _线索二叉树的作用。
- 线索二叉树的理解_ huangwei18351的博客-CSDN博客 _线索二叉树。
二叉排序树
引自:《数据结构教程》。
二叉排序树用于排序、查找/检索,可以大大提高查找的时间效率(在一般情况下,查询效率比链表结构要高)。二叉排序树又叫二叉查找树。有人说,当需要完成的功能是插入、删除和检索,二叉排序树具有比迄今为止研究过的任何数据结构都有更好的性能。
引自:二叉排序树(二叉查找树)及C语言实现 (biancheng.net)。
二叉排序树要么是空二叉树,要么具有如下特点:
- 二叉排序树中,如果其根结点有左子树,那么左子树上所有结点的值都小于根结点的值;
- 二叉排序树中,如果其根结点有右子树,那么右子树上所有结点的值都大小根结点的值;
- 二叉排序树的左右子树也要求都是二叉排序树;
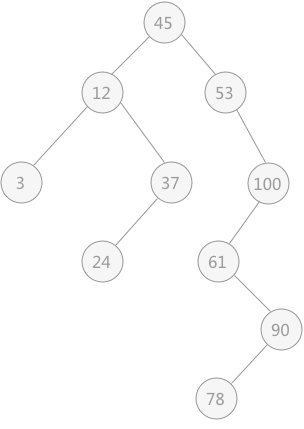
如下图所示就是一个二叉排序树。
引自:《数据结构教程》。
二叉排序树中插入数据,同样需要按照二叉排序树的原则进行。每次将一个新的元素插入到二叉排序树中,该元素对应的节点都是插在叶节点位置,插入的过程没有移动二叉树中其他节点。一个数据元素序列不一定按照值的大小进行排列,但当对其构造成为一棵二叉排序树以后,对该二叉排序树进行中序遍历得到的序列是一个按值大小排列的序列。
- 二叉排序树(二叉查找树)及C语言实现 (biancheng.net)。
- 二叉排序树_百度百科 (baidu.com)。
- 二叉查找树(BST)及二叉树的遍历_ 青萍之末的博客-CSDN博客 _二叉搜索树的遍历。
- 二分搜索树 | 菜鸟教程 (runoob.com)。
平衡二叉树(AVL树)
引自:平衡二叉树(AVL树)及C语言实现 (biancheng.net)。
平衡二叉树,又称为 AVL 树。实际上就是遵循以下两个特点的二叉树:
- 每棵子树中的左子树和右子树的深度差不能超过 1;
- 二叉树中每棵子树都要求是平衡二叉树;
其实就是在二叉树的基础上,若树中每棵子树都满足其左子树和右子树的深度差都不超过 1,则这棵二叉树就是平衡二叉树。
把二叉树中每个节点的左子树深度与右子树深度之差定义为该节点的平衡因子,因此平衡二叉树中每个节点的平衡因子只能是 1、0 或 -1。
引自:《数据结构教程》。
二叉排序树的形态,事先无法预料,随意性很大,得到的往往是一颗很不 “平衡” 的二叉树,深度差越大,其运算时间也越长,丧失了其优势。为了克服二叉排序树的这个缺陷,需要在插入和删除节点的同时对二叉树的形态结构进行必要的调整,使二叉排序树始终处于一种平衡状态。
…
理论上已经证明,具有 n 个节点的平衡树的深度在任何情况下都不会比具有相同节点数目的理想平衡数的深度高出 45% 以上。因此再平衡树上进行查找操作虽然比理想平衡树要慢一些,但通常比任意生成的二叉排序树中进行查找要快得多,其时间复杂度的数量级仍为O(Log_2(n))。
- 平衡二叉树(AVL树)及C语言实现 (biancheng.net)。
- AVL树(平衡二叉树)_ 青萍之末的博客-CSDN博客 _avl树是平衡二叉树吗。
红黑树
引自 红黑树(RB-Tree)_青萍之末的博客-CSDN博客。
红黑树是一种二叉查找树。
红黑树与AVL树的对比
- 如果插入一个节点引起了树的不平衡,AVL和RB-Tree都是最多只需要2次旋转操作,即两者都是O(1);但是在删除节点引起树的不平衡时,最坏情况下,AVL需要维护从被删节点到根节点这条路径上所有节点的平衡性,因此需要旋转的量级O(logN),而RB-Tree最多只需3次旋转,只需要O(1)的复杂度;
- 但是由于红黑树没有AVL树那么高度平衡,所以红黑树的查找性能相比AVL树要差一些,查找上的这一点性能差相比数据的插入和删除时的旋转性能是值得的,这就是为什么很多场合是用的红黑树,而不是AVL树,例如STL中的map和set。因此,RB-Tree在需要大量插入和删除节点的场景下效率更高。自然,由于AVL高度平衡,因此AVL的查找效率更高。
- 红黑树和AVL树的实现与比较—–算法导论 - 希隆囚徒 - 博客园 (cnblogs.com)。
- 红黑树(RB-tree)比AVL树的优势在哪?_mmshixing的博客-CSDN博客_红黑树的优点。
- 动画红黑树,旋转的艺术 - 知乎 (zhihu.com)。
其它树种和应用介绍
- B树和B+树_青萍之末的博客-CSDN博客 B树是对二叉查找树的改进,B树大量应用在数据库和文件系统当中。
- 浅谈二叉查找树、AVL树、红黑树、B树、B+树的原理及应用_青萍之末的博客-CSDN博客。
- 还有哈夫曼树、字典树等等树种。。
相关文章:
典型数据结构-栈/队列/链表、哈希查找、二叉树(BT)、线索二叉树、二叉排序树(BST树)、平衡二叉树(AVL树)、红黑树(RB树)
目录 典型数据结构列举 栈/队列/链表 树 二叉树 线索二叉树 二叉排序树 平衡二叉树(AVL树) 红黑树 其它树种和应用介绍 典型数据结构列举 栈/队列/链表 描述略。 一些基本的简单实现参考/数据结构简单实现/文件夹里面。 线性表详解ÿ…...

pyarmor 加密许可证的使用
一 pyarmor 许可证的用处 文档:5. 许可模式和许可证 — Pyarmor 8.3.6 文档 试用版本有如下的限制: 加密功能对脚本大小有限制,不能加密超过限制的大脚本。 混淆字符串功能在试用版中无法使用。 RFT 加密模式,BCC 加密模式在试…...

网络路径监控分析
不间断的连接应该是任何企业的首要任务。然而,确保网络中的源和目标之间持续、不间断的联系一直是网络通信中一个劳动密集型的过程。了解网络路径中的障碍、识别它们并迅速解决它们以维护健康、不间断的网络至关重要。 为什么要监控网络路径 维护网络运行状况是任…...

vue双向数据绑定是如何实现的?
Vue中的双向数据绑定主要是通过数据劫持和发布订阅模式来实现的。 数据劫持: Vue通过使用Object.defineProperty()方法来对data对象中的属性进行劫持,从而实现对数据的双向绑定。具体实现方式为: (1)在Vue实例化时&a…...

el-date-picker 封装一个简单的日期组件, 主要是禁用日期
子组件 <template><div><el-date-pickerv-model"dateModel"type"datetimerange":picker-options"pickerOptions"range-separator"至"ref"picker"start-placeholder"开始日期"end-placeholder&quo…...
保研复习-计算机组成原理
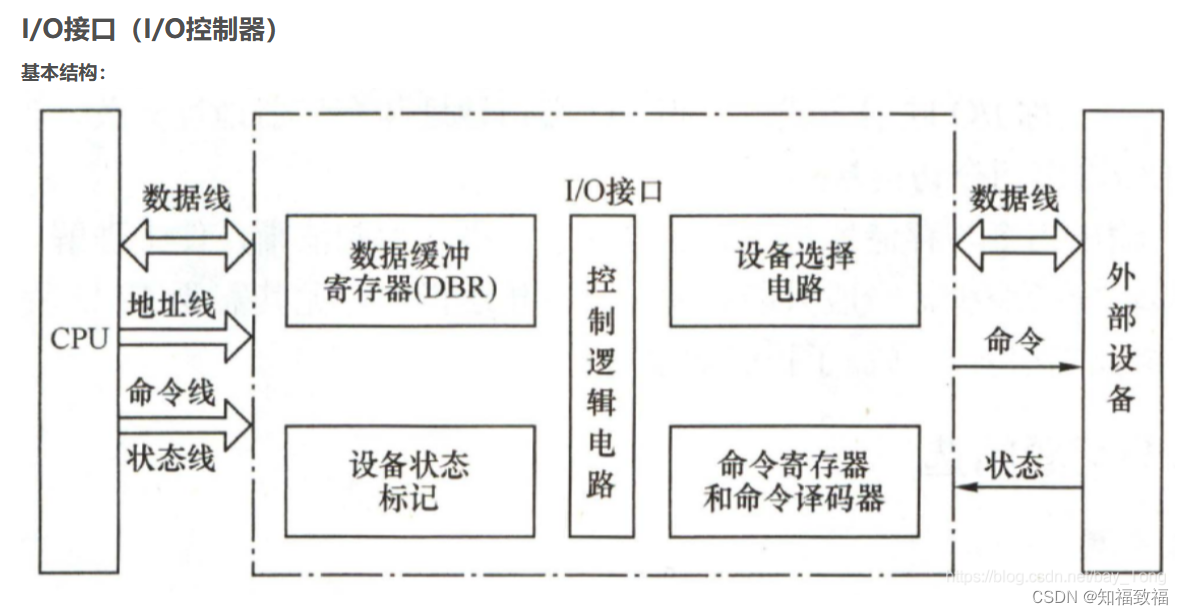
计算机组成原理 计算机组成冯诺依曼体系结构计算机系统的层次结构计算机的五大组成部件编译和解释的区别 CPUCPU的组成寄存器的类型指令类型指令功能指令执行过程 存储器存储器的层次结构寻址方式 输入和输出io方式有哪几种IO接口的基本结构 计算机组成 冯诺依曼体系结构 存储…...
linux环境安装redis(亲测完成)
linux环境安装redis 亲测完成 前言一、redis简介Redis 与其他 key - value 缓存产品有以下三个特点:Redis 优势 二、安装redis1.下载安装包2.创建服务器安装路径3.上传安装包4.解压安装包5.依赖安装6.编译 三、启动1)默认启动错误解决方式 2)指定配置启动2.1&#x…...

关于命令行交互自动化,及pyinstaller打包wexpect的问题
Python自动化工具 用来执行命令并进行交互,比如需要输入账号密码或者确认的场景 linux平台可以用pexpect,但是windows平台有一些差异,比较好用的是pexpect的变种wexpect,如果脚本中用了wexpect,并且要打包成onefile&a…...

8.4 【MySQL】文件系统对数据库的影响
因为 MySQL 的数据都是存在文件系统中的,就不得不受到文件系统的一些制约,这在数据库和表的命名、表的大小和性能方面体现的比较明显,比如下边这些方面: 数据库名称和表名称不得超过文件系统所允许的最大长度。 每个数据库都对应…...
Python WEB框架FastAPI (二)
Python WEB框架FastAPI (二) 最近一直在使用fastapi,随着使用的深入发现我对于它的了解还是太少了,以至于踩了一些坑。所以在这里记录一下,愿看到的小伙伴不迷路。 路径传参并发问题 一、路径传参 这是对上一个传参…...

基于Java网络书店商城设计实现(源码+lw+部署文档+讲解等)
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...
怒刷LeetCode的第3天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:动态规划 第二题 题目来源 题目内容 解决方法 方法一:模拟 方法二:数学规律 方法三:分组 第三题 题目来源 题目内容 解决方法 方法一:数学方法 方法…...

JavaScript数组去重常用方法
数组去重是在 JavaScript 开发中经常遇到的问题。本文将从前言、分析、使用场景、具体实现代码和注意事项等方面,详细讨论 JavaScript 数组去重的方法。 前言: 在 JavaScript 中,数组是一种常用的数据结构,用于存储多个值。然而…...
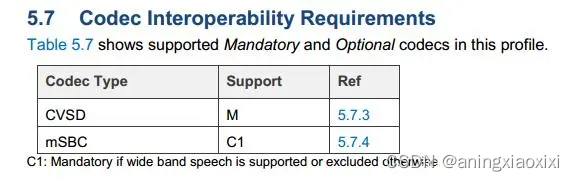
蓝牙电话之HFP—电话音频
1 媒体音频: 播放蓝牙音乐的数据,这种音频对质量要求高,数据发送有重传机制,从而以l2cap的数据形式走ACL链路。编码方式有:SBC、AAC、APTX、APTX_HD、LDAC这五种编码方式,最基础的编码方式是SBC࿰…...

JDBC基本概念
什么是JDBC JDBC概念 JDBC(Java DataBase Connectivity)是一套统一的基于Java语言的关系数据库编程接口规范。 该规范允许将SQL语句作为参数通过JDBC接口发送给远端数据库, …...

leetcode876 链表的中间节点
题目 给你单链表的头结点 head ,请你找出并返回链表的中间结点。 如果有两个中间结点,则返回第二个中间结点。 示例 输入:head [1,2,3,4,5] 输出:[3,4,5] 解释:链表只有一个中间结点,值为 3 。 输入&a…...

了解方法重写
父类 package com.mypackage.oop.demo07;//重写都是方法的重写,与属性无关 public class B {public static void test(){System.out.println("B>test.()");}public void test2(){System.out.println("B2>test.()");} }子类 package com…...

2、从“键鼠套装”到“全键盘游戏化”审核
1、风行内容仓的增效之路 - 前言 内容仓成立初期,安全审核组是规模最大的小组,占到部门人数的半壁江山,因此增效工作首先就从安全审核开始。 早期安全审核每天的达标值在800条左右,每天的总审核量不到1万,距离业务部门…...
【flutter】架构之商城main入口
架构之商城main入口 前言一、项目模块的划分二、入口main的配置三、配置文件怎么做总结 前言 本栏目我们将完成一个商城项目的架构搭建,并完善中间的所有功能,总页面大概200个,如果你能看完整个栏目,你肯定能独立完成flutter 项目…...
linux学习实操计划0103-安装软件
本系列内容全部给基于Ubuntu操作系统。 系统版本:#32~22.04.1-Ubuntu SMP PREEMPT_DYNAMIC Fri Aug 18 10:40:13 UTC 1 安装deb格式软件 Debian包是Unixar的标准归档,将包文件信息以及包内容,经过gzip和tar打包而成。 处理这些包的经典程序是…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...