当前位置： 首页 > news >正文

构造函数不能做为虚函数

news 2026/2/9 8:06:21

引用：windows程序员面试指南

构造函数不能做为虚函数

从存储空间角度
虚函数对应一个虚函数表，这大家都知道，可是这个虚函数表其实是存储在对象的内存空间的。问题出来了，如果构造函数是虚的，就需要通过虚函数表来调用，可是对象还没有实例化，也就是内存空间还没有，无法找到vtable，所以构造函数不能是虚函数。

从使用角度
虚函数的作用在于通过父类的指针或者引用来调用它的时候能够变成调用子类的那个成员函数。而构造函数是在创建对象时自动调用的，不可能通过父类的指针或者引用去调用，因此也就规定构造函数不能是虚函数。

相关文章：

构造函数不能做为虚函数

引用：windows程序员面试指南 构造函数不能做为虚函数 从存储空间角度 虚函数对应一个虚函数表，这大家都知道，可是这个虚函数表其实是存储在对象的内存空间的。问题出来了，如果构造函数是虚的，就需要通过虚函数表来调…...

编程日记 2023/9/20 16:37:34

持续集成实战 —— Jenkins自动化测试环境搭建

1.目的 在日常的项目测试过程中，搭建与维护测试环境是广大测试同学的一个基础技能，相信也很少会有公司完全不让测试去碰自己的测试环境。那么工作中大量的创建、部署、管理、维护等一系列的重复操作就成为了整个测试项目中一个巨大的工作量。 面对这样…...

编程日记 2023/9/20 16:36:32

ajax上传文件

背景 采用ajax传递表单内容和上传的文件 实现原理 使用FormData模拟表单数据，实现异步上传图片 代码 var formData new FormData(); formData.append("serviceId", param.serviceId); formData.append("keyId", param.keyId); formData.a…...

编程日记 2023/9/20 16:34:31

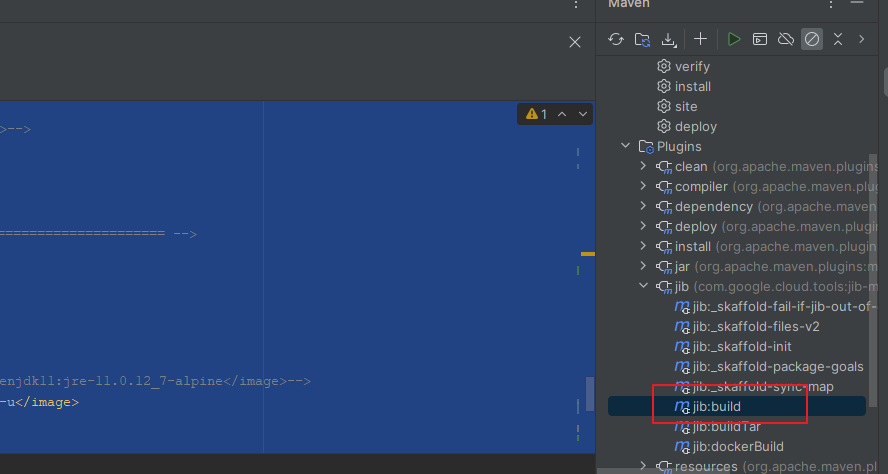
使用jib-maven-plugin插件构建镜像并推送至私服Harbor

jib-maven-plugin 插件配置 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apa…...

编程日记 2023/9/20 16:33:30

道路空间功率谱密度与时间功率谱密度（笔记）

0.随机路面 仿真时间200秒 车速15m/s 采样间隔0.25秒&#xff08;4Hz&#xff09; A级路面平均振幅&#xff1a;0.0044米 B级路面平均振幅&#xff1a;0.0087米 C级路面平均振幅&#xff1a;0.0173米 D级路面平均振幅&#xff1a;0.0346米 1.先上代码其中之一 clc clear clo…...

编程日记 2023/9/20 16:31:27

JMeter接口测试之文件上传

最近用JMeter做接口测试&#xff0c;频繁遇到了文件上传的接口&#xff0c;与其他一般接口的处理方式不一样&#xff0c;想着分享下&#xff0c;希望能给测试同学一点启发。 文章将围绕三个部分进行展开&#xff1a; 一、用户场景 二、接口请求参数 三、JMeter脚本编写步骤…...

编程日记 2023/9/20 16:30:26

自动化测试需知的4项测试工具！

一般来说学自动化会建议大家先学selenium&#xff0c;因为最早的时候&#xff0c;自动化就代表selenium&#xff0c;进入测试行业就开始做接口测试&#xff0c;而且现在基本每个公司都需要接口测试。今天就和大家聊一下接口测试的工具。 一、Robot Framework 机器人框架。之所…...

编程日记 2023/9/20 16:29:25

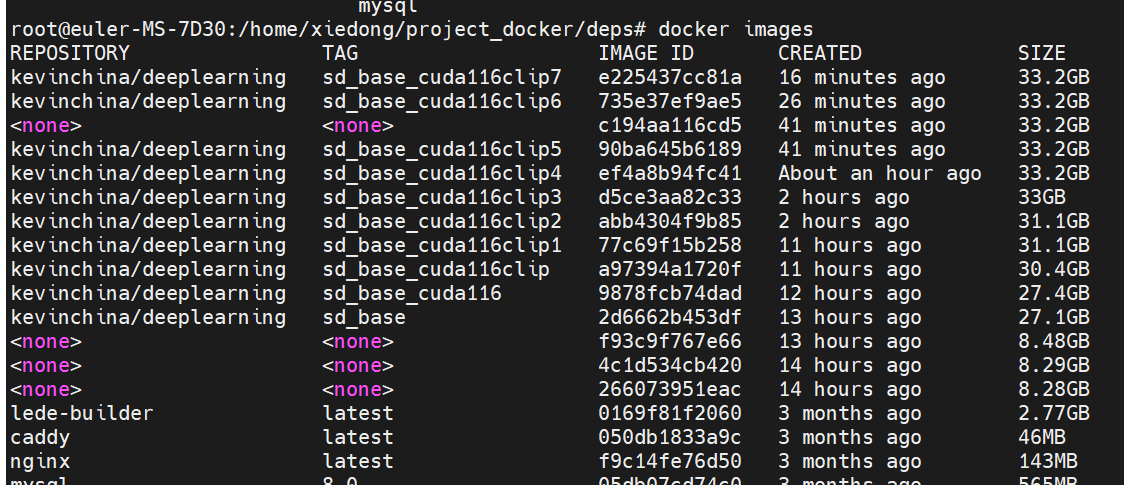
【深度学习】clip-interrogator clip docker 容器启动过程

文章目录 dockerfile备忘ENTRYPOINT ["bash", "/app/startProject.sh"]常用docker指令web服务脚本访问接口文件 给一张图片&#xff0c;输出图片描述。 dockerfile备忘 只有从dockerfile制作的镜像才有分层结构&#xff0c;加速传输&#xff0c;故第一步…...

编程日记 2023/9/20 16:28:24

Linux设备驱动之gpio-keys

Linux设备驱动之gpio-keys 前两个章节介绍了Linux字符设备和platform设备的注册&#xff0c;他们都是比较基础的&#xff0c;让大家理解Linux内核的设备驱动是如何注册、使用的。但在工作中&#xff0c;个人认为完全手写一个字符设备驱动的机会比较少&#xff0c;更多的都是基…...

编程日记 2023/9/20 16:27:23

【vue3页面展示代码】展示代码codemirror插件

技术版本&#xff1a; vue 3.2.40、codemirror 6.0.1、less 4.1.3、vue-codemirror 6.1.1、 codemirror/lang-vue 0.1.2、codemirror/theme-one-dark 6.1.2 效果图&#xff1a; 1.安装插件 yarn add codemirror vue-codemirror codemirror/lang-vue codemirror/theme-one-dar…...

编程日记 2023/9/20 16:26:20

【面试必刷TOP101】链表相加 单链表的排序

目录 题目&#xff1a;链表相加(二)_牛客题霸_牛客网 (nowcoder.com) 题目的接口&#xff1a; 解题思路&#xff1a; 代码&#xff1a; 过啦&#xff01;&#xff01;&#xff01; 题目&#xff1a;单链表的排序_牛客题霸_牛客网 (nowcoder.com) 题目的接口&#xff1a;…...

编程日记 2023/9/20 16:25:19

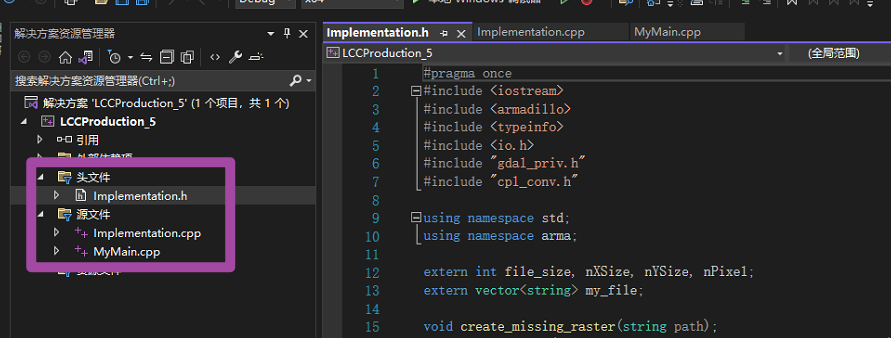
Visual Studio复制、拷贝C++项目与第三方库配置信息到新的项目中

本文介绍在Visual Studio软件中&#xff0c;复制一个已有的、配置过多种第三方库的C项目&#xff0c;将其拷贝为一个新的项目&#xff0c;同时使得新项目可以直接使用原有项目中配置好的各类**C**配置、第三方库等的方法。 在撰写C 代码时&#xff0c;如果需要用到他人撰写的第…...

编程日记 2023/9/20 16:24:18

rust迭代器

迭代器用来遍历容器。 迭代器就是把容器中的所有元素按照顺序一个接一个的传递给处理逻辑。 Rust中的迭代器 标准库中定义了Iterator特性 trait Iterator {type Item;fn next(&mut self) -> Option<Self::Item>; }实现了Iterator特性的结构体就是迭代器。 很多类…...

编程日记 2023/9/20 16:23:17

软件定制开发的优势与步骤|APP搭建|小程序

软件定制开发的优势与步骤|APP搭建|小程序 定制开发的优势&#xff1a; 1. 满足特定需求&#xff1a;定制开发可以根据客户的实际需求进行设计和开发&#xff0c;使得软件系统能够更好地满足客户的业务目标。 2. 优化用户体验&#xff1a;通过深入了解客户的需求&#xff0c;定…...

编程日记 2023/9/20 16:22:17

ERR_CONNECTION_REFUSED等非标准的HTTP错误状态码原因分析和解决办法

文章目录 一、DNS Resolution Failed1&#xff0c;DNS服务器故障2&#xff0c;DNS配置错误3&#xff0c;DNS劫持4&#xff0c;域名过期-5&#xff0c;其他网络问题 二、ERR_CONNECTION_REFUSED-"ERR_CONNECTION_REFUSED" 错误可能有多种原因 三、ERR_SSL_PROTOCOL_ER…...

编程日记 2023/9/20 16:21:16

瀑布流 - Vue3基于Grid布局简单实现一个瀑布流组件

瀑布流 - Vue3基于Grid布局简单实现一个瀑布流组件 前言 在学习Grid布局之时&#xff0c;我发现其是CSS中的一种强大的布局方案&#xff0c;它将网页划分成一个个网格&#xff0c;可以任意组合不同的网格&#xff0c;做出各种各样的布局&#xff0c;在刷某书和某宝首页时&…...

编程日记 2023/9/20 16:18:13

ES6面试题总结

1. 谈谈你对 ES6 的理解,为什么要学习es6? ES6是新一代的JS语言标准&#xff0c;对分JS语言核心内容做了升级优化&#xff0c;规范了JS使用标准&#xff0c;新增了JS原生方法&#xff0c;使得JS使用更加规范&#xff0c;更加优雅&#xff0c;更适合大型应用的开发。学习ES6是成…...

编程日记 2023/9/20 16:15:10

mybatisplus，jdbc 批量插入

1.测试用例 项目中遇到在做导入号码的时候我们会用到批量导入&#xff0c;提高入库的速度。接下来我们以10000条为测试用例。 1.1 批量执行sql语句 当需要成批插入或者更新记录时&#xff0c;可以采用Java的批量更新机制&#xff0c;这一机制允许多条语句一次性提交给数据库…...

编程日记 2023/9/20 16:14:09

如何使用IP归属地查询API来追踪网络活动

引言 在当今数字化世界中&#xff0c;了解网络活动的源头和位置对于网络安全、市场研究和用户体验至关重要。IP归属地查询API是一种强大的工具&#xff0c;可以帮助您追踪网络活动并获取有关IP地址的重要信息。本文将探讨如何使用IP归属地查询API来追踪网络活动&#xff0c;以…...

编程日记 2023/9/20 16:12:06

【SQL】S0 系列博文大纲

系列博文大纲 SQL 学习环境建议系列博文相关书籍系列博文大纲阶段进展 SQL 学习环境建议 对于 SQL 语言的学习&#xff0c;博主本地使用&#xff1a;MySQL DataGrip&#xff1b; MySQL 提供本地数据库服务&#xff1b; DataGrip IDE&#xff0c;承担编程运行测试任务&#xf…...

编程日记 2023/9/20 16:11:05

Qt Widget类解析与代码注释

#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码&#xff0c;写上注释 当然可以&#xff01;这段代码是 Qt …...

编程新知 2025/11/29 21:00:30

深入理解JavaScript设计模式之单例模式

目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式&#xff08;Singleton Pattern&#…...

编程新知 2026/1/31 17:09:43

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力

引言&#xff1a; 在人工智能快速发展的浪潮中&#xff0c;快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型&#xff08;LLM&#xff09;。该模型代表着该领域的重大突破&#xff0c;通过独特方式融合思考与非思考…...

编程新知 2026/2/6 19:29:20

Python实现prophet 理论及参数优化

文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候&#xff0c;写过一篇简单实现&#xff0c;后期随着对该模型的深入研究&#xff0c;本次记录涉及到prophet 的公式以及参数调优&#xff0c;从公式可以更直观…...

编程新知 2026/1/27 5:01:54

Rust 异步编程

Rust 异步编程 引言 Rust 是一种系统编程语言，以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天，异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

编程新知 2025/11/17 18:58:56

Unit 1 深度强化学习简介

Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库&#xff0c;例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体&#xff0c;比如 SnowballFight、Huggy the Do…...

编程新知 2026/2/8 12:54:53

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台

🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型（LLM）的广泛应用，开发者常面临多个挑战： 各大模型（OpenAI、Claude、Gemini、Ollama）接口风格不统一；缺乏一个统一平台进行模型调用与测试；本地模型 Ollama 的集成与前…...

编程新知 2026/1/25 3:31:07

网站指纹识别

网站指纹识别 网站的最基本组成&#xff1a;服务器&#xff08;操作系统&#xff09;、中间件&#xff08;web容器&#xff09;、脚本语言、数据厍 为什么要了解这些&#xff1f;举个例子&#xff1a;发现了一个文件读取漏洞&#xff0c;我们需要读/etc/passwd&#xff0c;如…...

编程新知 2026/2/2 17:06:29

快刀集(1): 一刀斩断视频片头广告

一刀流&#xff1a;用一个简单脚本&#xff0c;秒杀视频片头广告&#xff0c;还你清爽观影体验。 1. 引子 作为一个爱生活、爱学习、爱收藏高清资源的老码农&#xff0c;平时写代码之余看看电影、补补片&#xff0c;是再正常不过的事。 电影嘛&#xff0c;要沉浸&#xff0c;…...

编程新知 2026/1/8 0:40:27

基于Springboot+Vue的办公管理系统

角色&#xff1a; 管理员、员工 技术&#xff1a; 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能&#xff1a; 该办公管理系统是一个综合性的企业内部管理平台&#xff0c;旨在提升企业运营效率和员工管理水…...

编程新知 2026/1/31 8:55:37