经典算法-----约瑟夫问题(C语言)
目录
前言
故事背景
约瑟夫问题
环形链表解决
数组解决
前言
今天我们来玩一个有意思的题目,也就是约瑟夫问题,这个问题出自于欧洲中世纪的一个故事,下面我们就去通过编程的方式来解决这个有趣的问题,一起来看看吧!

故事背景
据说著名犹太历史学家Josephus有过以下的故事:在罗马人占领乔塔帕特后,39 个犹太人与Josephus及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而Josephus 和他的朋友并不想遵从。首先从一个人开始,越过k-2个人(因为第一个人已经被越过),并杀掉第k个人。接着,再越过k-1个人,并杀掉第k个人。这个过程沿着圆圈一直进行,直到最终只剩下一个人留下,这个人就可以继续活着。问题是,给定了和,一开始要站在什么地方才能避免被处决。Josephus要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。
17世纪的法国数学家加斯帕在《数目的游戏问题》中讲了这样一个故事:15个教徒和15 个非教徒在深海上遇险,必须将一半的人投入海中,其余的人才能幸免于难,于是想了一个办法:30个人围成一圆圈,从第一个人开始依次报数,每数到第九个人就将他扔入大海,如此循环进行直到仅余15个人为止。问怎样排法,才能使每次投入大海的都是非教徒。

约瑟夫问题
从键盘获取两个数据,n和s,n是表示人数,s是表示从第一个人开始数,数到第s个的时候那个人就出局,问:最后剩下的最后一个人是第几个?
环形链表解决
这里我们可以去通过环形链表的形式来解决这个问题 ,过程图如下所示:

先根据当前输入的人数去创建一个相对应的环形链表,依次把每个人的位置存入进去

然后就去从第一个人开始数,当数到第三个人的时候就进行删除操作,如下所示,后面就从第四个节点开始新的一轮……

代码如下所示:
#include <stdio.h>
#include<stdlib.h>
//节点
typedef struct node {int num;struct node* next;
}Node;//创建一个环形链表
Node* create_list(int n) {Node* head, * tail;head = tail = NULL;for (int i = 0; i < n; i++) {Node* p = (Node*)malloc(sizeof(Node));p->num = i + 1; //依次标记当前位置if (head == NULL) {head = p;tail = p;head->next = NULL;}else{tail->next = p;tail = p;}tail->next = head;}return head; //返回头结点
}int main() {int n, s;printf("请输入:");scanf("%d %d", &n, &s);Node* cur = create_list(n);int count = 1; //此时cur指向的是第一个节点,所以count为1while (n != 1) { //当n=1时候,结束循环,此时剩下最后一个人count++;//先进行count统计if (count == s) {n--; //进行删除节点操作Node* del_node = cur->next; cur->next = del_node->next;free(del_node);//释放掉这个节点//此时count回归到1,也就是重新开始新的一轮count = 1;}cur = cur->next;}printf("最后剩下的是:%d\n", cur->num);
}数组解决
不同与链表的是,数组不能去自定义人的数量,也就是说这里数组的数量是提前写好了的,还有就是数组的执行效率更加高,环形链表要去通过遍历执行,时间复杂度为O(n),而数组可以去直接找到这个位置时间复杂度为O(1),不需要去一个一个遍历,代码如下:
//数组实现
#include<stdio.h>
void function(int* num, int length, int s, int start) {int count = 0;int i = start - 1;//标记起始位置int n = length; //当前人数while (n != 1) {i = (i + s - 1) % n; //下一个出局人的位置for (int j = i + 1; j < length; j++)num[j - 1] = num[j]; //进行删除操作,把要删除的数字后面的依次往前移动,覆盖掉这个要删除的数字n--;//删除操作完成,减少一个人if (i == n) { //当i超出数组范围的时候,i就回归到第一个为止i = 0;}}printf("最后一个 :%d", num[i]);return;
}int main() {int num[6];//这里就已经定义好了6个人int s; //每次数到s,出局一个printf("请输入:");scanf("%d", &s);for (int i = 0; i < sizeof(num) / sizeof(int); i++)num[i] = i+1;function(num, sizeof(num) / sizeof(int), s, 0);
}以上就是今天的内容,我们下次见!
分享一张壁纸:
相关文章:

经典算法-----约瑟夫问题(C语言)
目录 前言 故事背景 约瑟夫问题 环形链表解决 数组解决 前言 今天我们来玩一个有意思的题目,也就是约瑟夫问题,这个问题出自于欧洲中世纪的一个故事,下面我们就去通过编程的方式来解决这个有趣的问题,一起来看看吧!…...

代码随想录 动态规划Ⅴ
494. 目标和 给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 或 - ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ,在 1 之前添加 - …...
驱动DAY9
驱动文件 #include <linux/init.h> #include <linux/module.h> #include <linux/of.h> #include <linux/of_gpio.h> #include <linux/gpio.h> #include <linux/fs.h> #include <linux/io.h> #include <linux/device.h> #incl…...

03贪心:摆动序列
03贪心:摆动序列 376. 摆动序列 局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。 整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列。…...

javascript获取元素在浏览器中工作区域的左、右、上、下距离,或带滚动条的元素在页面中的大小
//获取元素在包含元素框中的大小 //第1个函数为获取元素在包含元素中左内边框的距离 function getELementLeft(element){//获取元素在包含元素左边距离var actualeftelement.offsetLeft;//获取元素的上级包含元素var currentelement.offsetParent;//循环到一直没有包含元素whil…...
VSCode 安装使用教程 环境安装配置 保姆级教程
一个好用的 IDE 不仅能提升我们的开发效率,还能让我们保持愉悦的心情,这样才是非常 Nice 的状态 ^_^ 那么,什么是 IDE 呢 ? what IDE(Integrated Development Environment,集成开发环境)是含代码…...
c盘中temp可以删除吗?appdata\local\temp可以删除吗?
http://www.win10d.com/jiaocheng/22594.html C盘AppData文件夹是一个系统文件夹,里面存储着临时文件,各种应用的自定义设置,快速启动文件等。近期有用户发现appdata\local\temp占用了大量的空间,那么该文件可以删除吗?…...

Java手写聚类算法
Java手写聚类算法 1. 算法思维导图 以下是聚类算法的实现原理的思维导图,使用Mermanid代码表示: #mermaid-svg-AK9EgYRS38PkRJI4 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-AK9EgYRS38…...
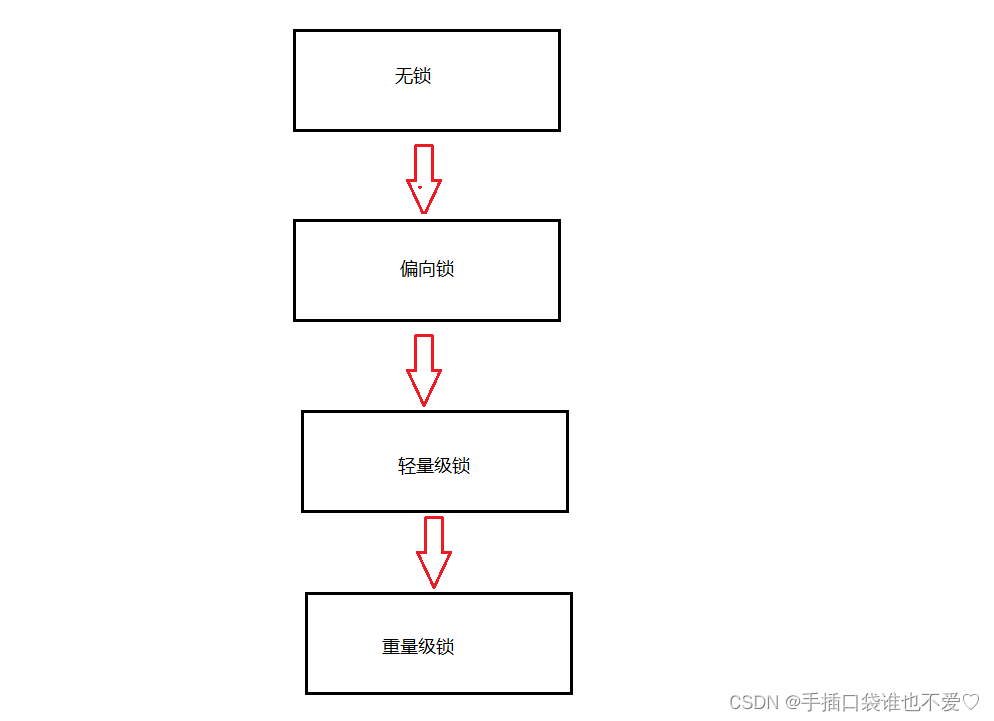
解密Java多线程中的锁机制:CAS与Synchronized的工作原理及优化策略
目录 CAS什么是CASCAS的应用ABA问题异常举例 Synchronized 原理基本特征加锁过程偏向锁轻量级锁重量级锁 其他优化操作锁消除锁粗化 CAS 什么是CAS CAS: 全称Compare and swap,字面意思:”比较并交换“,CAS涉及如下操作: 假设内存中的原数据…...

solid works草图绘制与设置零件特征的使用说明
(1)草图绘制 • 草图块 在 FeatureManager 设计树中,您可以隐藏和显示草图的单个块。您还可以查看块是欠定义 (-)、过定义 () 还是完全定义。 要隐藏和显示草图的单个块,请在 FeatureManager 设计树中右键单击草图块,…...
页面跳转后,该页面不刷新问题)
vue3使用router.push()页面跳转后,该页面不刷新问题
文章目录 原因分析最优解决 原因分析 这是一个常见问题,当使用push的时候,会向history栈添加一个新记录,这个时候,再添加一个完全相同的路由时,就不会再次刷新了 最优解决 在页面跳转时加上params参数时间 router.…...

如何理解数字工厂管理系统的本质
随着科技的飞速发展和数字化转型的推动,数字工厂管理系统逐渐成为工业4.0时代的重要工具。数字工厂系统旨在整合和优化工厂运营的各个环节,通过实时数据分析和处理,提升生产效率,降低成本,并增强企业的整体竞争力。为了…...
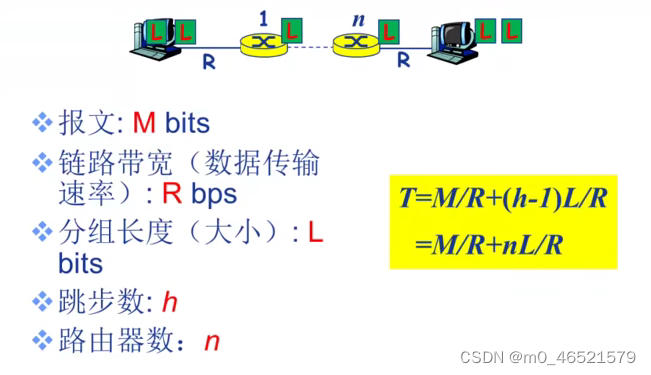
笔记1.3 数据交换
如何实现数据通过网络核心从源主机到达目的主机? 数据交换 交换网络: 动态转接动态分配传输资源 数据交换类型: (1)电路交换 (2)报文交换 (3)分组交换 电路交换的特…...
实时车辆行人多目标检测与跟踪系统(含UI界面,Python代码)
算法架构: 目标检测:yolov5 目标跟踪:OCSort其中, Yolov5 带有详细的训练步骤,可以根据训练文档,训练自己的数据集,及其方便。 另外后续 目标检测会添加 yolov7 、yolox,目标跟踪会…...

谷歌AI机器人Bard发布强大更新,支持插件功能并增强事实核查;全面整理高质量的人工智能、机器学习、大数据等技术资料
🦉 AI新闻 🚀 谷歌AI机器人Bard发布强大更新,支持插件功能并增强事实核查 摘要:谷歌的人工智能聊天机器人Bard发布了一项重大更新,增加了对谷歌应用的插件支持,包括 Gmail、Docs、Drive 等,并…...

NI SCXI-1125 数字量控制模块
NI SCXI-1125 是 NI(National Instruments)生产的数字量控制模块,通常用于工业自动化和控制系统中,以进行数字输入和输出控制。以下是该模块的一些主要产品特点: 数字量输入:SCXI-1125 模块通常具有多个数字…...
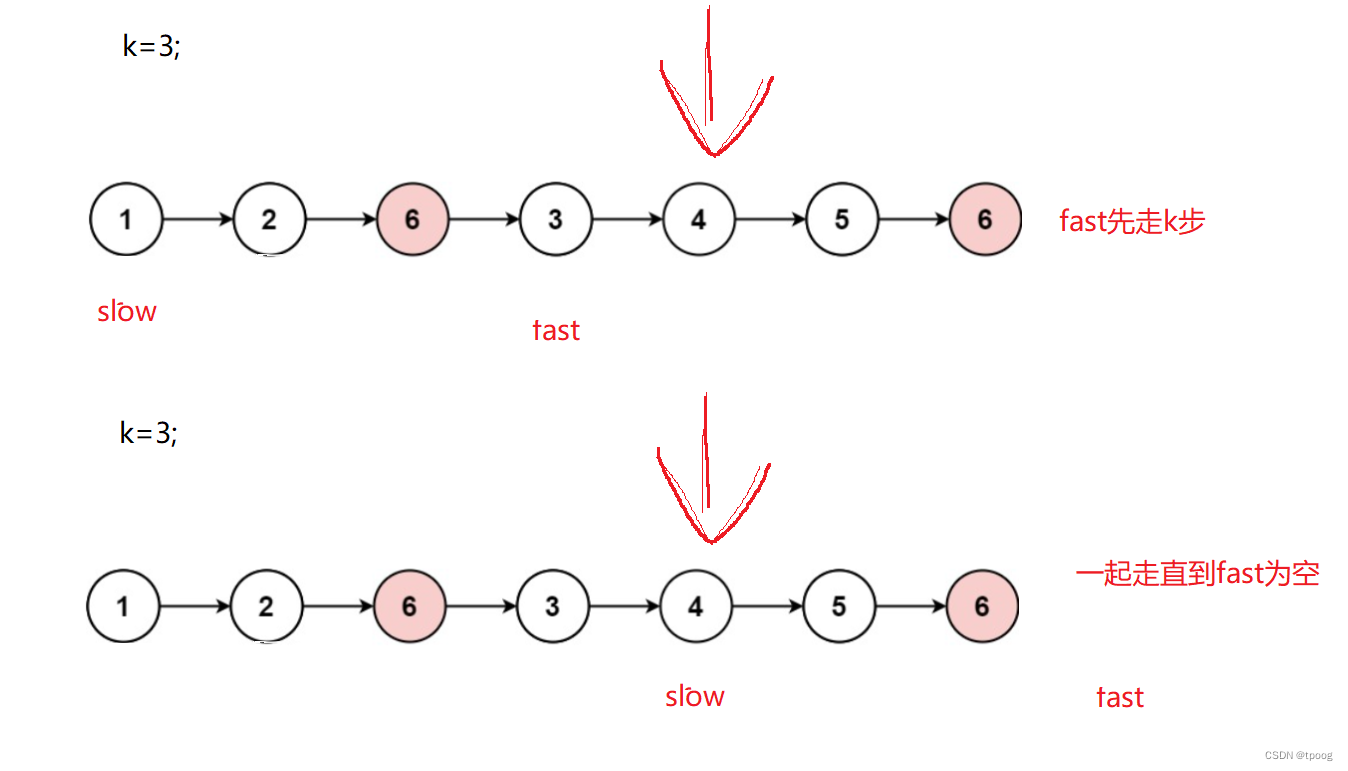
链表oj题1(Leetcode)——移除链表元素,反转链表,链表的中间节点,
链表OJ 一,移除链表元素1.1分析1.2代码 二,找到链表的中间节点2.1分析2.2代码 三,反转链表3.1分析3.2代码 四,找到链表中倒数第k个节点4.1分析4.2代码 一,移除链表元素 移除链表元素 1.1分析 这里的删除要分成两种…...
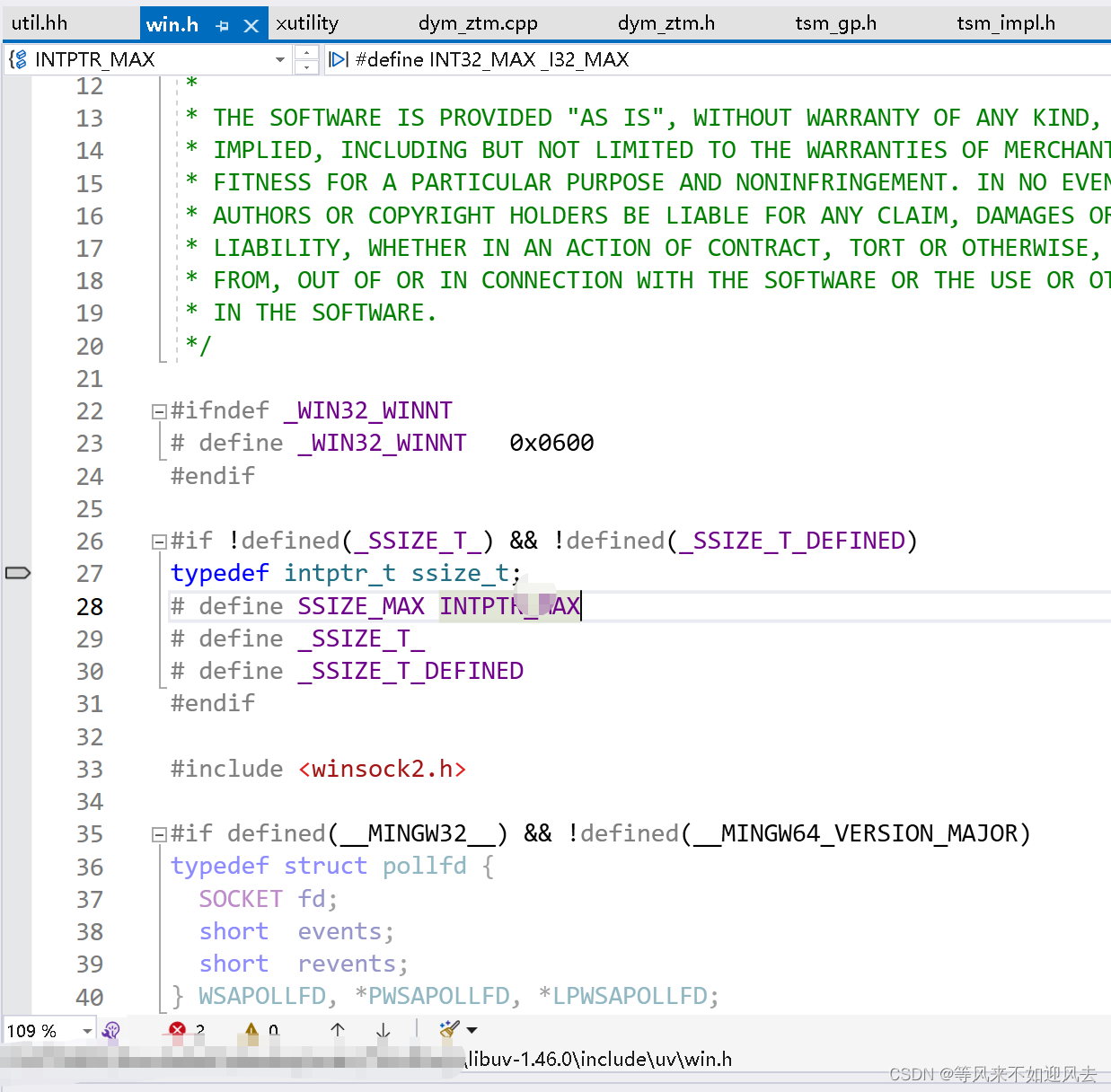
【libuv】与uvgrtrp的_SSIZE_T_定义不同
libuv的 #if !defined(_SSIZE_T_) && !defined(_SSIZE_T_DEFINED) typedef intptr_t ssize_t;...

安卓ROM定制 修改必备常识-----初步了解system系统分区文件夹的基本含义 【二】
安卓修改rom 固件 修改GSI 移植rom 必备常识 lib--**so文件基本解析 一起来了解system目录相应文件的用途吧。(rom版本不同里面的app也会不一样) 简单打开img格式后缀文件 给大家说下最简单的方法提取img里面的文件,对于后缀img格式的文件可…...

GPT会统治人类吗
一 前言 花了大概两天时间看完《这就是ChatGPT》,触动还是挺大的,让我静下来,认真地想一想,是否真正理解了ChatGPT,又能给我们以什么样的启发。 二 思考 在工作和生活中,使用ChatGPT或文心一言,…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...
