如何判断linux 文件(或lib)是由uclibc还是glibc编译出来的?
工作中使用的编译环境有2套编译器,一个是glibc,一个是uclibc。
有些项目使用的glibc编译的lib,和使用uclibc编译的工程,在一起就会出现reference的编译错误如下:
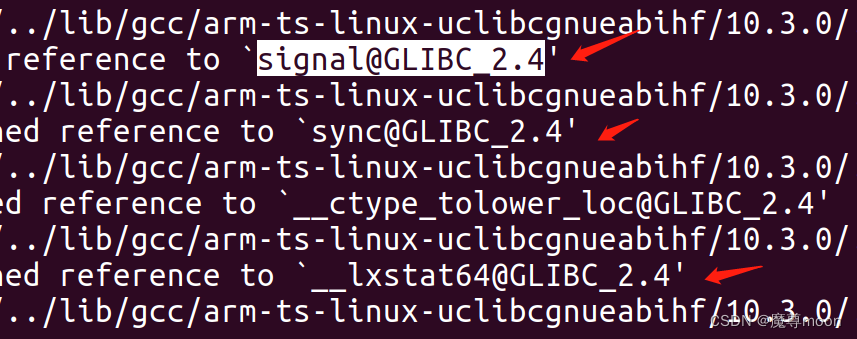
那和如何来判断一个文件是由哪个编译器编译的呢?
试了几个方法,file 不行, objdump 也不行。 可以的命令如下:
strings -a libpcap.so.1.9.1 | grep -i uclibc

可以看到,使用这个命令,如果这个lib是由 uclibc 编译的,会类似grep出一些字串。
而如果这个lib是由 glibc 编译出来的,就不会grep任何的信息

灵活运用strings命令可以完成其他的功能,之前看的帖子给的例子是看编译器版本的
strings -a program_name | grep -i gcc
我改动之后可以完成我的需求。
相关文章:

如何判断linux 文件(或lib)是由uclibc还是glibc编译出来的?
工作中使用的编译环境有2套编译器,一个是glibc,一个是uclibc。 有些项目使用的glibc编译的lib,和使用uclibc编译的工程,在一起就会出现reference的编译错误如下: 那和如何来判断一个文件是由哪个编译器编译的呢&#…...

WorkPlus | 好用、专业、安全的局域网即时通讯及协同办公平台
自国家于2022年发布的《关于加强数字政府建设的指导意见》以来,我国数字政府建设已经迈入了一个全新的里程碑,迎来了全面改革和深化升级的全新阶段。 WorkPlus作为自主可控、可信安全、专属定制的数字化平台,扮演着政务机关、政府单位以及各…...

ARM Linux DIY(十二)NES 游戏
文章目录 前言交叉编译工具链使能 Cnes 游戏模拟器移植游戏手柄调试 前言 很多小伙伴为了不让自己的 V3s 吃灰,进而将其打造成游戏机。 我们 DIY 的板子具备屏幕、扬声器、USB Host(可以接游戏手柄),当然也要凑一凑热闹。 交叉编…...

MOEA算法的背景知识
MOEA算法 多目标进化算法优化MOEA工作原理举个例子 为什么单一策略可能会导致种群中的个体过于相似?种群在MOEA里面做什么?举例说明 多目标进化算法优化MOEA Multi-objective evolutionary algorithm optimization (MOEA) 多目标进化算法优化࿰…...
【rtp-benchmarks】读取本地文件基于uvgRtp实现多线程发送
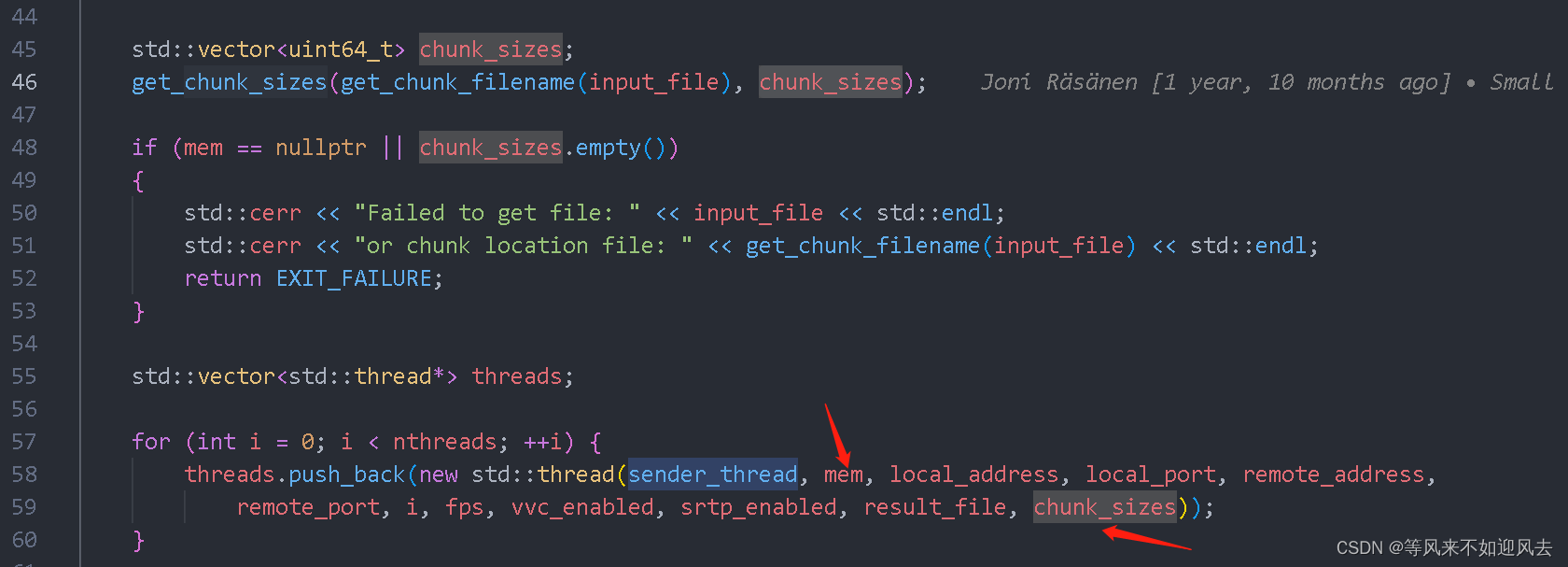
input 文件做内存映射 : get_mem D:\XTRANS\soup\uvg-rtp-dev\rtp-benchmarks\util\util.cc 文件中读取chunksize 到 vector 里作为chunks 创建多个线程进行发送 std::vector<std::thread*> threads;...
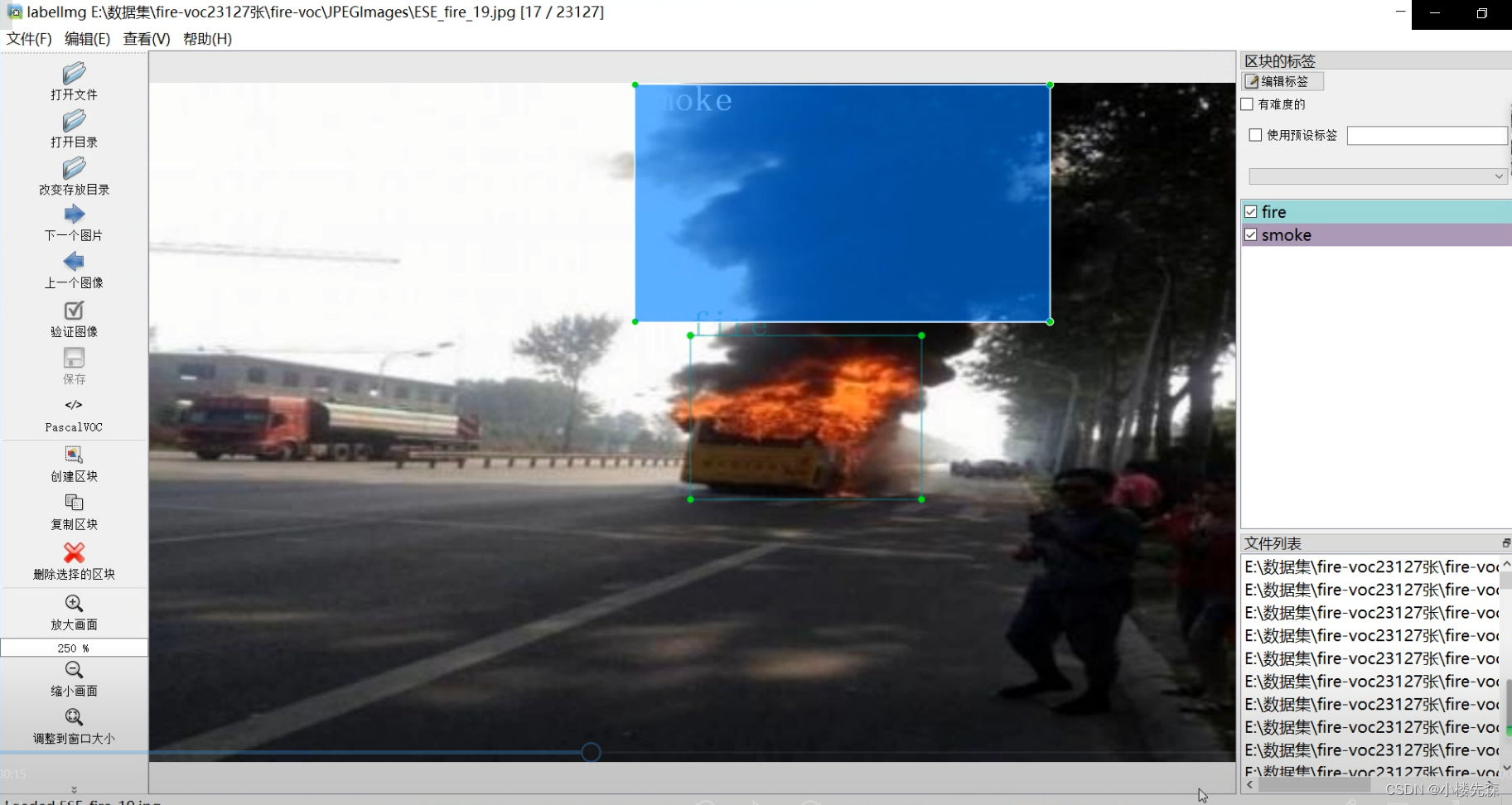
fire-voc 火光 烟火 火灾 目标检测数据集
一年中最容易引发火灾的季节是在冬季,主要原因有这样几点。 1、秋冬季节,随着用火、用电、用气增加,加上天气干燥,棉花、木材 、衣物等物体内含有的水分也较低。2、秋冬季风力较大,一旦有火苗冒起就很容易随风蔓延,是火灾的高发期。3、春季也是火灾多发季节&#x…...

【力扣1462】课程表(拓扑排序+bitset优化到O(n))
题目描述: 你总共需要上 numCourses 门课,课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ,其中 prerequisites[i] [ai, bi] 表示如果你想选 bi 课程,你 必须 先选 ai 课程。 有的课会有直接的先修课程&am…...
【AI】机器学习——支持向量机(非线性及分析)
5. 支持向量机(线性SVM) 文章目录 5.4 非线性可分SVM5.4.1 非线性可分问题处理思路核技巧核函数特点 核函数作用于SVM 5.4.2 正定核函数由 K ( x , z ) K(x,z) K(x,z) 构造 H \mathcal{H} H 空间步骤 常用核函数 5.5 SVM参数求解算法5.6 SVM与线性模型关系 5.4 非线性可分SVM …...
2023-09-20 LeetCode每日一题(拿硬币)
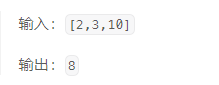
2023-09-20每日一题 一、题目编号 LCP 06. 拿硬币二、题目链接 点击跳转到题目位置 三、题目描述 桌上有 n 堆力扣币,每堆的数量保存在数组 coins 中。我们每次可以选择任意一堆,拿走其中的一枚或者两枚,求拿完所有力扣币的最少次数。 示…...
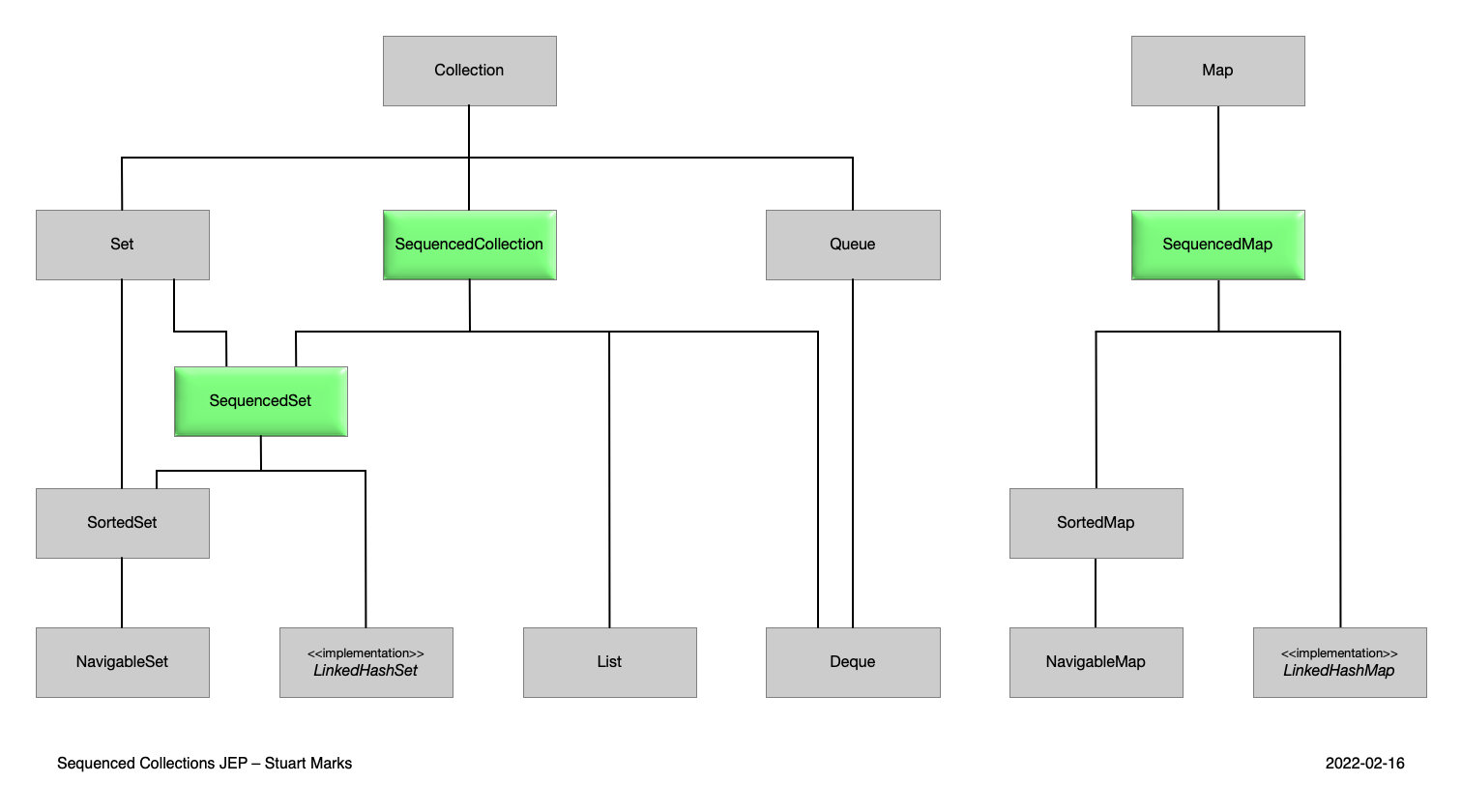
Java21的新特性
Java语言特性系列 Java5的新特性Java6的新特性Java7的新特性Java8的新特性Java9的新特性Java10的新特性Java11的新特性Java12的新特性Java13的新特性Java14的新特性Java15的新特性Java16的新特性Java17的新特性Java18的新特性Java19的新特性Java20的新特性Java21的新特性Java22…...
测试-----selenuim webDriver
文章目录 1.页面导航2.元素定位3. 浏览器操作4.获取元素信息5. 鼠标的操作6. 键盘操作7. 元素等待8.下拉框9.弹出框10.滚动条11.frame处理12.验证码处理(cookie) 1.页面导航 首先是导入对应的包 :from selenium import webdriver然后实例化:driver web…...

21天学会C++:Day12----初始化列表
CSDN的uu们,大家好。这里是C入门的第十一讲。 座右铭:前路坎坷,披荆斩棘,扶摇直上。 博客主页: 姬如祎 收录专栏:C专题 目录 1. 初始化列表 1.1 引入 1.2 初始化列表 1.3 初始化列表的注意事项 1.…...
OpenAI开发系列(二):大语言模型发展史及Transformer架构详解
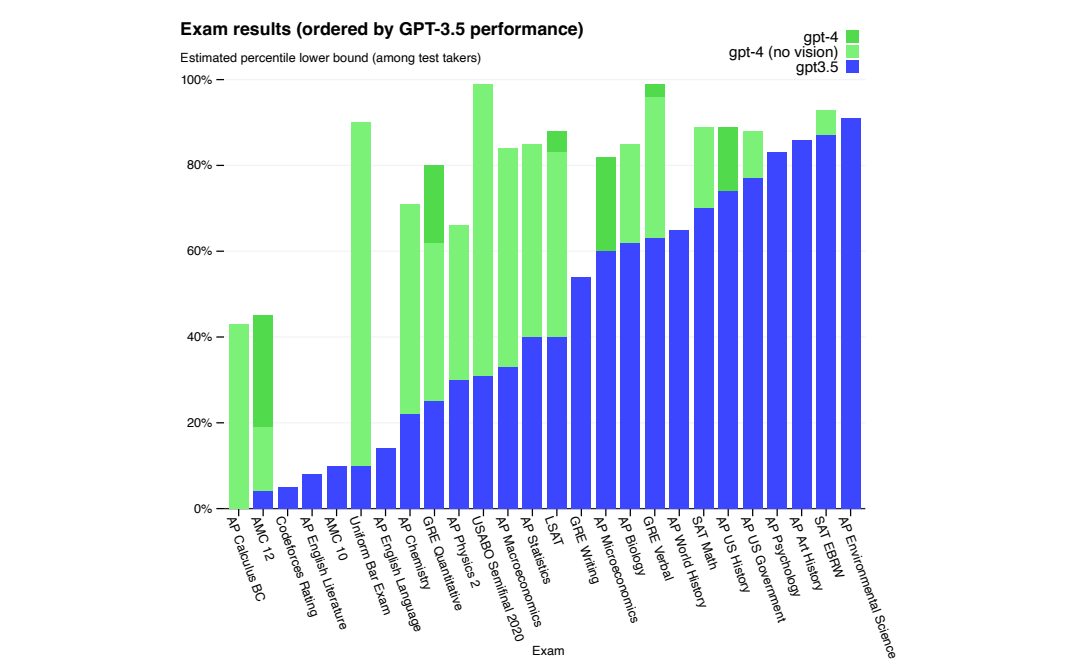
全文共1.8w余字,预计阅读时间约60分钟 | 满满干货,建议收藏! 一、介绍 在2020年秋季,GPT-3因其在社交媒体上病毒式的传播而引发了广泛关注。这款拥有超过1.75亿参数和每秒运行成本达到100万美元的大型语言模型(Large …...

Gson - 一个Java序列化/反序列化库
官网 GitHub - google/gson: A Java serialization/deserialization library to convert Java Objects into JSON and back 项目简介 一个Java序列化/反序列化库,用于将Java对象转换为JSON和返回JSON。 Gson is a Java library that can be used to convert Java…...
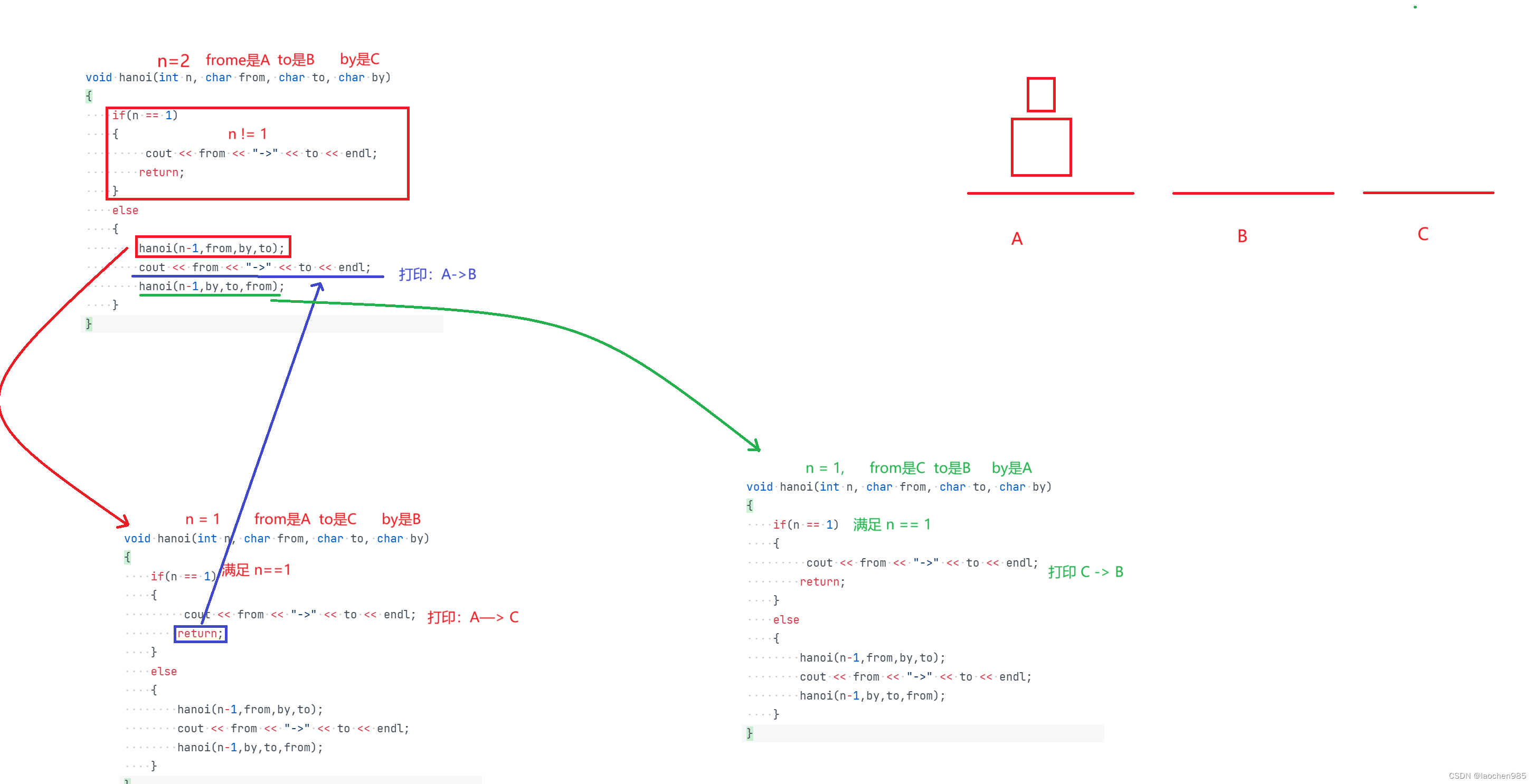
6-1 汉诺塔
汉诺(Hanoi)塔问题是一个经典的递归问题。 设有A、B、C三个塔座;开始时,在塔座A上有若干个圆盘,这些圆盘自下而上,由大到小地叠在一起。要求将塔座A上的圆盘移到塔座B上,并仍按同样顺序叠放。在…...
添加密码登录验证)
Linux之initd管理系统(海思、ZYNQ、复旦微)添加密码登录验证
设置root用户密码:passwd命令设置密码,即修改/etc/passwd文件 一、串口提示输入用户名密码方法 修改 /etc/inittab 方法一: 增加: ::askfirst:-/bin/login 注释: #::respawn:/sbin/getty -L ttyS000 115200 vt…...
怎么更改代理ip,代理ip如何切换使用?
我们要如何使用HTTP代理,对它进行切换使用呢? 如果你购买了青果网络的HTTP代理,可以在文档这边获取使用方法: 可以在这里调试: 也可以在这里选择key提取。 如果有的朋友们想利用利用python,每隔30秒使用API…...
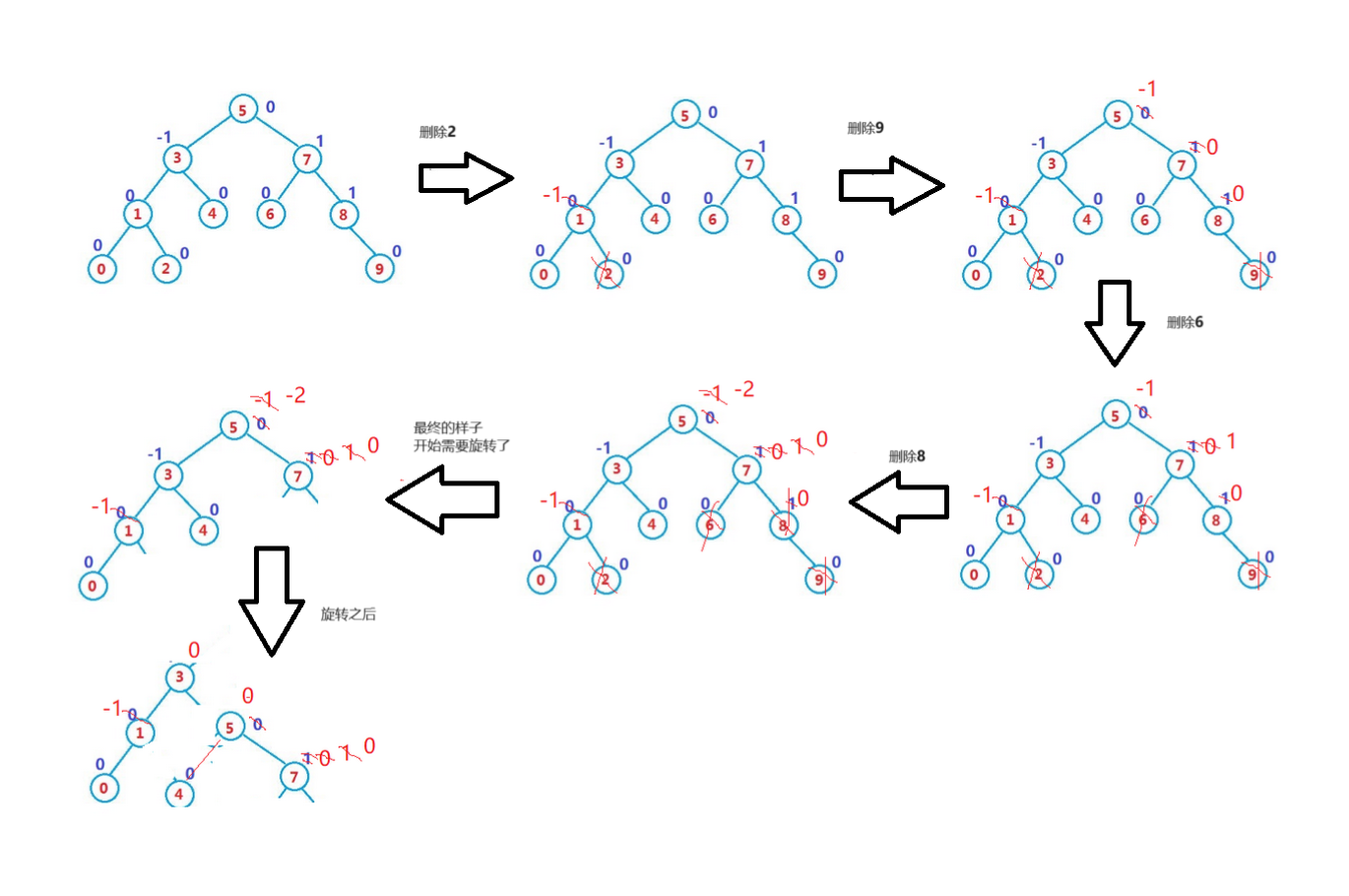
【C++从0到王者】第三十三站:AVL树
文章目录 前言一、AVL 树的概念二、AVL树的实现1. AVL树的结点定义2. AVL树的插入之插入部分3. AVL树的插入之平衡因子的改变4. AVL树的插入之左旋5. AVL树的左旋抽象图6.AVL树的右旋抽象图7. AVL树的双旋8. AVL树的右左双旋9. AVL树的右左双旋的本质10. AVL树的左右双旋11. AV…...

手机机型响应式设置2
window.screen.height:屏幕高度 window.innerHeight:视口高度(去除浏览器头尾的高度) document.body.clientHeight:内容高度 vh:网页视口高度的1/100 vw:网页视口宽度的1/100 vmaxÿ…...

uni-app 之 解决u-button始终居中问题
uView中u-button始终居中问题如何解决的简单方法? 1:给该元素margin-right: 0;可以达到向右靠齐; 2:给该元素的父元素设置float: right image.png <u-button style"width: 50px; margin-left: 0;" plain"t…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

C# winform教程(二)----checkbox
一、作用 提供一个用户选择或者不选的状态,这是一个可以多选的控件。 二、属性 其实功能大差不差,除了特殊的几个外,与button基本相同,所有说几个独有的 checkbox属性 名称内容含义appearance控件外观可以变成按钮形状checkali…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
