6-1 汉诺塔
汉诺(Hanoi)塔问题是一个经典的递归问题。
设有A、B、C三个塔座;开始时,在塔座A上有若干个圆盘,这些圆盘自下而上,由大到小地叠在一起。要求将塔座A上的圆盘移到塔座B上,并仍按同样顺序叠放。在移动过程中要求遵守如下规则:
- 每次只能移动一个圆盘;
- 任何时刻都不允许将较大的圆盘压在较小的圆盘之上;
- 在满足前两条规则的前提下,可将圆盘移至A、B、C中任何一塔座上。
- 例如,3个圆盘的初始状态如下
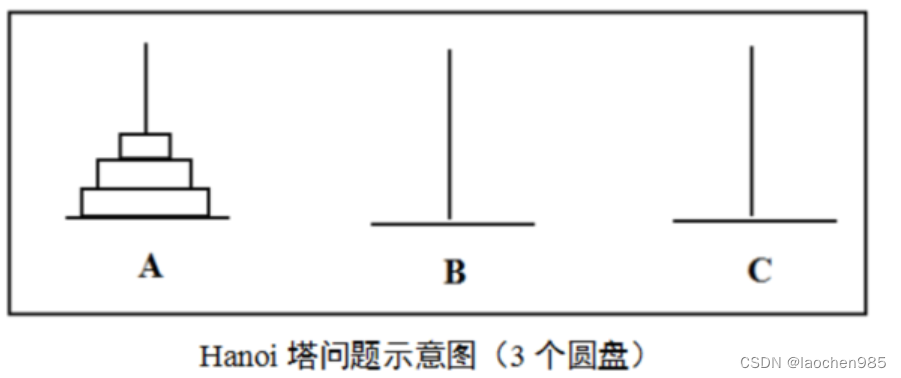
则移动过程如下:
A->B
A->C
B->C
A->B
C->A
C->B
A->B
要求实现一个递归函数,模拟输出n(1<=n<=8)个圆盘从塔座A借助塔座C移动到塔座B上的过程(用A->B表示将圆盘从A移到B,其他类似)。
函数接口定义:
void hanoi(int n, char from, char to, char by);其中参数 n是圆盘数 、from是原来叠放圆盘的塔座 、to是最终叠放圆盘的塔座 、by是可借助的塔座。
裁判测试程序样例:
#include<iostream>
using namespace std;//将n个圆盘借助by从from移到to
void hanoi(int n, char from, char to, char by);//输入n,输出将原来在A上的n个圆盘借助C移动到B上的移动过程,控制到文件尾
int main() {int n, cnt=0;while(cin>>n) {cnt++;if (cnt>1) cout<<endl;hanoi(n, 'A', 'B', 'C');}return 0;
}输入样例:
3
4
输出样例:
A->B
A->C
B->C
A->B
C->A
C->B
A->BA->C
A->B
C->B
A->C
B->A
B->C
A->C
A->B
C->B
C->A
B->A
C->B
A->C
A->B
C->B## 答案:
void hanoi(int n, char from, char to, char by)
{if(n == 1){cout << from << "->" << to << endl;return;}else{hanoi(n-1,from,by,to);cout << from << "->" << to << endl;hanoi(n-1,by,to,from);}
}## 思路:
汉诺塔问题是一个经典的递归问题,它描述了一种将一堆圆盘从一个塔座移动到另一个塔座的问题,同时需要遵守一些规则。问题的规则如下:
- 有三个塔座,通常称为A、B、C。
- 初始时,在塔座A上有若干个圆盘,这些圆盘自下而上,由大到小地叠在一起。
- 目标是将塔座A上的所有圆盘移动到塔座B上,并仍然按照相同的顺序叠放。
- 每次只能移动一个圆盘。
- 任何时刻都不允许将较大的圆盘放在较小的圆盘之上。
- 在满足前两条规则的前提下,可以将圆盘从A、B、C中的任何一个塔座移动到另一个塔座。
汉诺塔问题的目标是找到一种移动方案,将所有圆盘从起始塔座A移动到目标塔座B,中间可以借助辅助塔座C。这个问题可以通过递归算法来解决。
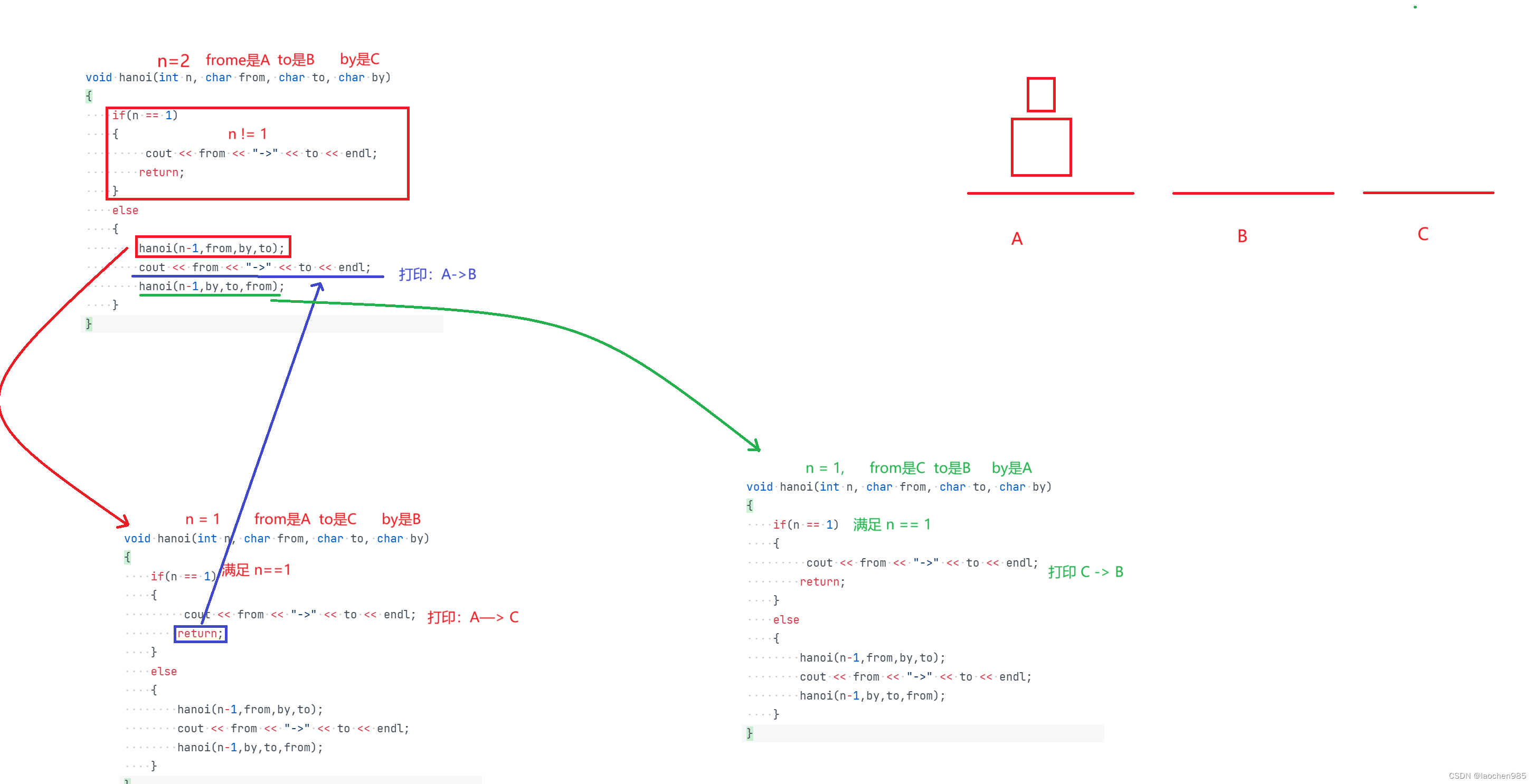
下面是一个详细解释递归函数 hanoi 的实现和工作原理:
void hanoi(int n, char from, char to, char by) {if (n == 1) {cout << from << "->" << to << endl;return;}// 递归步骤:// 1. 将前 n-1 个圆盘从起始塔座(from)经过目标塔座(by)移动到辅助塔座(by)上hanoi(n - 1, from, by, to);// 2. 将最大的圆盘从起始塔座(from)移动到目标塔座(to)上,并输出移动过程cout << from << "->" << to << endl;// 3. 将前 n-1 个圆盘从辅助塔座(by)经过起始塔座(from)移动到目标塔座(to)上hanoi(n - 1, by, to, from);
}
工作原理解释:
-
如果
n等于 1,表示只有一个圆盘需要移动,直接将它从from移动到to,并输出移动过程。 -
如果
n大于 1,表示有多个圆盘需要移动。递归的过程如下:-
第一步:将前
n-1个圆盘从起始塔座from经过目标塔座to移动到辅助塔座by上。这一步使用了递归调用,因为它也是一个汉诺塔问题,只不过规模减小了。 -
第二步:将最大的圆盘从起始塔座
from移动到目标塔座to上,并输出移动过程。这是实际的移动步骤。 -
第三步:将前
n-1个圆盘从辅助塔座by经过起始塔座from移动到目标塔座to上。这一步同样使用了递归调用。
-
这个递归过程会一直持续到只剩下一个圆盘需要移动,然后问题就会逐级返回,完成了所有圆盘的移动。
通过这种递归方法,你可以模拟汉诺塔问题的解决过程,并输出移动步骤。
相关文章:

6-1 汉诺塔
汉诺(Hanoi)塔问题是一个经典的递归问题。 设有A、B、C三个塔座;开始时,在塔座A上有若干个圆盘,这些圆盘自下而上,由大到小地叠在一起。要求将塔座A上的圆盘移到塔座B上,并仍按同样顺序叠放。在…...
添加密码登录验证)
Linux之initd管理系统(海思、ZYNQ、复旦微)添加密码登录验证
设置root用户密码:passwd命令设置密码,即修改/etc/passwd文件 一、串口提示输入用户名密码方法 修改 /etc/inittab 方法一: 增加: ::askfirst:-/bin/login 注释: #::respawn:/sbin/getty -L ttyS000 115200 vt…...
怎么更改代理ip,代理ip如何切换使用?
我们要如何使用HTTP代理,对它进行切换使用呢? 如果你购买了青果网络的HTTP代理,可以在文档这边获取使用方法: 可以在这里调试: 也可以在这里选择key提取。 如果有的朋友们想利用利用python,每隔30秒使用API…...
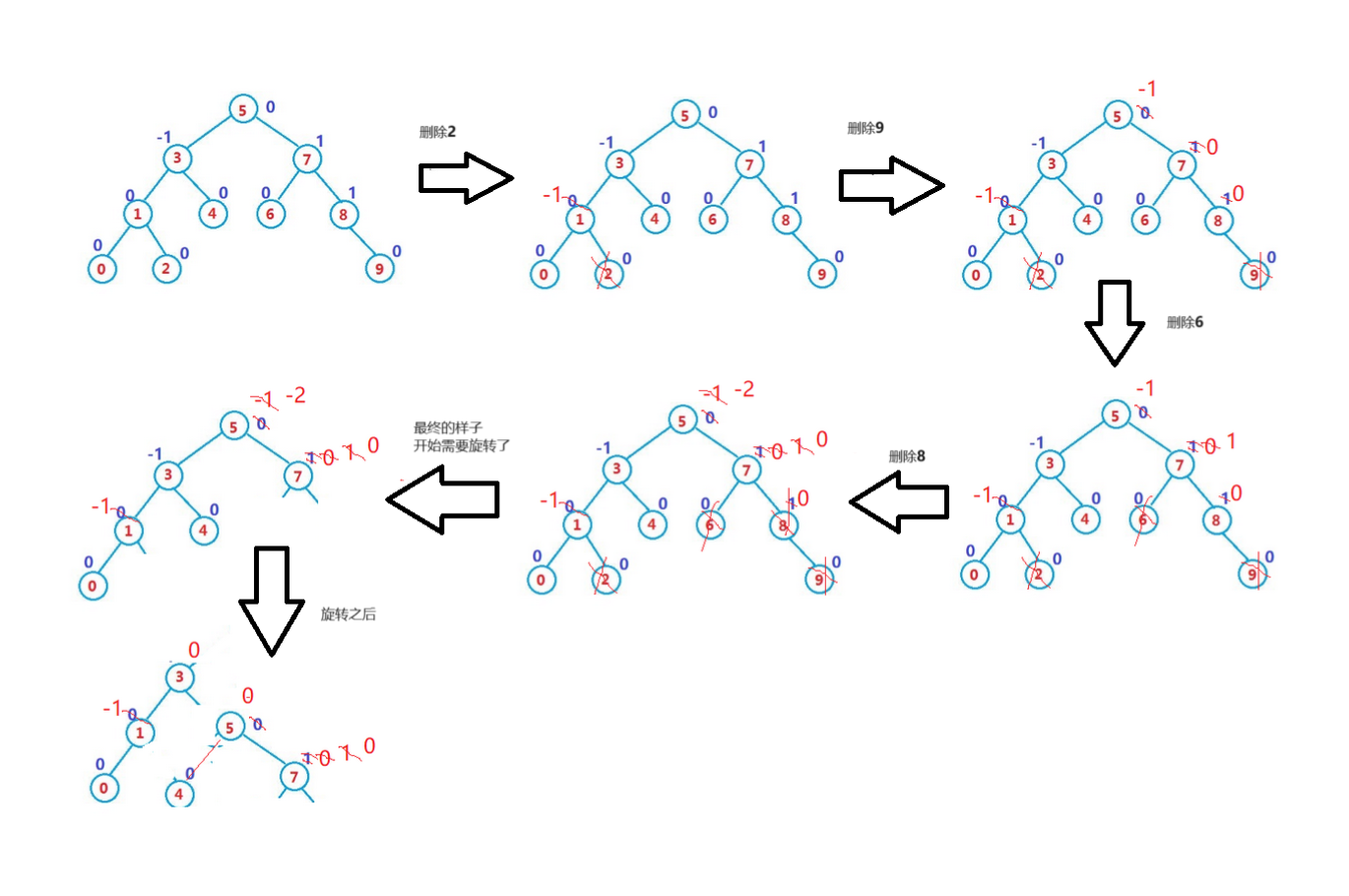
【C++从0到王者】第三十三站:AVL树
文章目录 前言一、AVL 树的概念二、AVL树的实现1. AVL树的结点定义2. AVL树的插入之插入部分3. AVL树的插入之平衡因子的改变4. AVL树的插入之左旋5. AVL树的左旋抽象图6.AVL树的右旋抽象图7. AVL树的双旋8. AVL树的右左双旋9. AVL树的右左双旋的本质10. AVL树的左右双旋11. AV…...

手机机型响应式设置2
window.screen.height:屏幕高度 window.innerHeight:视口高度(去除浏览器头尾的高度) document.body.clientHeight:内容高度 vh:网页视口高度的1/100 vw:网页视口宽度的1/100 vmaxÿ…...

uni-app 之 解决u-button始终居中问题
uView中u-button始终居中问题如何解决的简单方法? 1:给该元素margin-right: 0;可以达到向右靠齐; 2:给该元素的父元素设置float: right image.png <u-button style"width: 50px; margin-left: 0;" plain"t…...

Python日期处理库:掌握时间的艺术
💂 个人网站:【工具大全】【游戏大全】【神级源码资源网】🤟 前端学习课程:👉【28个案例趣学前端】【400个JS面试题】💅 寻找学习交流、摸鱼划水的小伙伴,请点击【摸鱼学习交流群】 日期和时间在计算机编程…...

JOSEF约瑟 智能电流继电器KWJL-20/L KWLD26 零序孔径45mm 柜内导轨式安装
KWJL-20智能电流继电器 零序互感器: KWLD80 KWLD45 KWLD26 KWJL-20 一、产品概述 KWJL-20系列智能剩余电流继电器(以下简称继电器)适用于交流电压至660V或更高的TN、TT、和IT系统,频率为50Hz。通过零序电流互感器检测出超过…...

NLP技术如何为搜索引擎赋能
目录 1. NLP关键词提取与匹配在搜索引擎中的应用1. 关键词提取例子 2. 关键词匹配例子 Python实现 2. NLP语义搜索在搜索引擎中的应用1. 语义搜索的定义例子 2. 语义搜索的重要性例子 Python/PyTorch实现 3. NLP个性化搜索建议在搜索引擎中的应用1. 个性化搜索建议的定义例子 2…...

演唱会没买到票?VR直播为你弥补遗憾
听说周杰伦开了演唱会?没买到票的人是不是有着大大的遗憾呢?很多时候大型活动、演唱会都会因为场地限制而导致很多人未能有缘得见,而且加上票价成本高,“黄牛票”事件频出,我们的钱包受不住啊!!…...

myabtis的缓存级别
文章目录 MyBatis缓存的区别是什么作用范围方面有哪些差异生命周期数据进行了存储缓存的优缺点 MyBatis缓存的区别是什么 MyBatis 提供了一级缓存和二级缓存,这两者的主要区别在于其作用范围和生命周期。 一级缓存:一级缓存是 SqlSession 级别的缓存。…...
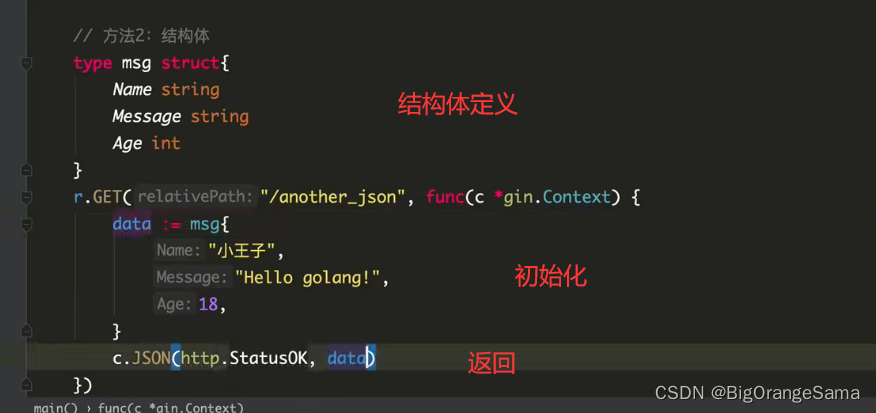
gin框架再探
Gin框架介绍及使用 | 李文周的博客 (liwenzhou.com) lesson03_gin框架初识_哔哩哔哩_bilibili 1.路由引擎 //路由引擎 rgin.Default() 2.一些http请求方法 get post put delete等等 遇到什么路径,执行什么函数 r.GET("/hello",func{做你想做的事返回…...

经典算法-----约瑟夫问题(C语言)
目录 前言 故事背景 约瑟夫问题 环形链表解决 数组解决 前言 今天我们来玩一个有意思的题目,也就是约瑟夫问题,这个问题出自于欧洲中世纪的一个故事,下面我们就去通过编程的方式来解决这个有趣的问题,一起来看看吧!…...

代码随想录 动态规划Ⅴ
494. 目标和 给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 或 - ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ,在 1 之前添加 - …...
驱动DAY9
驱动文件 #include <linux/init.h> #include <linux/module.h> #include <linux/of.h> #include <linux/of_gpio.h> #include <linux/gpio.h> #include <linux/fs.h> #include <linux/io.h> #include <linux/device.h> #incl…...

03贪心:摆动序列
03贪心:摆动序列 376. 摆动序列 局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。 整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列。…...

javascript获取元素在浏览器中工作区域的左、右、上、下距离,或带滚动条的元素在页面中的大小
//获取元素在包含元素框中的大小 //第1个函数为获取元素在包含元素中左内边框的距离 function getELementLeft(element){//获取元素在包含元素左边距离var actualeftelement.offsetLeft;//获取元素的上级包含元素var currentelement.offsetParent;//循环到一直没有包含元素whil…...
VSCode 安装使用教程 环境安装配置 保姆级教程
一个好用的 IDE 不仅能提升我们的开发效率,还能让我们保持愉悦的心情,这样才是非常 Nice 的状态 ^_^ 那么,什么是 IDE 呢 ? what IDE(Integrated Development Environment,集成开发环境)是含代码…...
c盘中temp可以删除吗?appdata\local\temp可以删除吗?
http://www.win10d.com/jiaocheng/22594.html C盘AppData文件夹是一个系统文件夹,里面存储着临时文件,各种应用的自定义设置,快速启动文件等。近期有用户发现appdata\local\temp占用了大量的空间,那么该文件可以删除吗?…...

Java手写聚类算法
Java手写聚类算法 1. 算法思维导图 以下是聚类算法的实现原理的思维导图,使用Mermanid代码表示: #mermaid-svg-AK9EgYRS38PkRJI4 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-AK9EgYRS38…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...
