利用PCA科学确定各个指标的权重系数
背景参考:
1、提取主成分
- 对样本进行PCA分析,查看不同变量贡献率,确定主要的指标。
我们可以通过下列代码获取需要的所有数据:
import numpy as np
from sklearn.decomposition import PCA# 创建一个数据
np.random.seed(0)
data = np.random.random((100,5))
y = np.random.randint(0,6,100)# 进行pca
pca = PCA()
x_new = pca.fit_transform(data)# 获取每个特征对于每个主成分的贡献率
explained_variance_ratio = pca.explained_variance_ratio_
print("排序的贡献率:",explained_variance_ratio)# 获取每个特征对于每个主成分的特征值(排序了的)
explained_variance = pca.explained_variance_
print("排序的特征值:",explained_variance)# 获取每个特征对于每个主成分的特征值(未排序的)
cov_matrix = np.cov(data.T) # 计算协方差矩阵
eigen_values, eigen_vectors = np.linalg.eig(cov_matrix) # 计算特征值和特征向量
print("未排序的特征值:",eigen_values)# 获取载荷系数,即特征向量
components = pca.components_
print("排序的载荷系数,即特征向量:\n",components) # 行代表主成分,即第一行为第一主成分
我们获得输出如下:
排序的贡献率: [0.2679184 0.22563357 0.20109877 0.16265843 0.14269083]
排序的特征值: [0.11390347 0.09592639 0.08549561 0.06915299 0.06066392]
未排序的特征值: [0.11390347 0.09592639 0.08549561 0.06066392 0.06915299]
排序的载荷系数,即特征向量:[[ 0.2792074 0.32459124 0.54648931 0.5063108 0.51154917][ 0.38799128 -0.41011012 0.47386964 -0.6498715 0.18543747][-0.48817892 0.14380819 -0.23333252 -0.33626022 0.75728829][-0.11980573 -0.83842108 -0.10090177 0.45633566 0.25352175][-0.72030127 -0.05309911 0.64200605 -0.00179817 -0.25723834]]
2、计算各个变量的权重系数
- 从上述结果中我们可以看出,前4个主成分的贡献率达到了85.73%,因此我们可以说所有指标基本可以由前四个主成分对应的指标代替(通过未排序的特征值确定是那几个指标)。
- 随后我们计算这四个主成分的线性组合公式。计算这四个主成分的线性组合公式,我们需要计算他们的系数。
-
确定主成分在各线性组合中的系数。
在之前,我们先假设这5个变量分别是:a1、a2、a3、a4、a5。他们的系数分别是: λ 1 \lambda _{1} λ1、 λ 2 \lambda _{2} λ2、 λ 3 \lambda _{3} λ3、 λ 4 \lambda _{4} λ4、 λ 5 \lambda _{5} λ5。
公式: 系数 = 载荷系数 / 对应主成分的特征值的开方
即: λ i = L i j V i ,其中: L i j 代表第 i 个主成分中第 j 个载荷的数值, V i 代表第 i 个主成分的特征值。 \lambda _{i}= \frac{L_{ij}}{\sqrt{V_{i}}} , 其中:L_{ij}代表第i个主成分中第j个载荷的数值,V_{i}代表第i个主成分的特征值。 λi=ViLij,其中:Lij代表第i个主成分中第j个载荷的数值,Vi代表第i个主成分的特征值。
例如第一主成分的线性组合公式:
λ 1 = 0.2792074 0.11390347 = 0.82729 \lambda _{1}=\frac{0.2792074}{\sqrt{0.11390347}} = 0.82729 λ1=0.113903470.2792074=0.82729
λ 2 = 0.32459124 0.11390347 = 0.96176 \lambda _{2}=\frac{0.32459124}{\sqrt{0.11390347}} = 0.96176 λ2=0.113903470.32459124=0.96176
λ 3 = 0.54648931 0.11390347 = 1.61924 \lambda _{3}=\frac{0.54648931}{\sqrt{0.11390347}} = 1.61924 λ3=0.113903470.54648931=1.61924
λ 4 = 0.5063108 0.11390347 = 1.50019 \lambda _{4}=\frac{0.5063108}{\sqrt{0.11390347}} = 1.50019 λ4=0.113903470.5063108=1.50019
λ 5 = 0.51154917 0.11390347 = 1.51572 \lambda _{5}=\frac{0.51154917}{\sqrt{0.11390347}} = 1.51572 λ5=
-
相关文章:

利用PCA科学确定各个指标的权重系数
背景参考: 1、提取主成分 对样本进行PCA分析,查看不同变量贡献率,确定主要的指标。我们可以通过下列代码获取需要的所有数据: import numpy as np from sklearn.decomposition import PCA# 创建一个数据 np.random.seed(0) data = np.random.random((100,5)) y = np.ra…...

代码随想录 -- day55 --392.判断子序列 、115.不同的子序列
392.判断子序列 dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度为dp[i][j]。 if (s[i - 1] t[j - 1]) t中找到了一个字符在s中也出现了if (s[i - 1] ! t[j - 1]) 相当于t要删除元素,继续匹配 if (s…...

mysql5升级到mysql8的血泪教训
核心问题1:下载中断这个包就会有问题,下载中断的话一定要重新下载 核心问题2:低版本向高版本迁移 无法整库备份 只能单库备份 1.数据备份 我这里备份了全库,所以后面数据没恢复回来,把DDL语句拆出来了单独建表 mysqldump -u root -p --al…...
Unity 开发人员转CGE(castle Game engine)城堡游戏引擎指导手册
Unity 开发人员的城堡游戏引擎概述 一、简介2. Unity相当于什么GameObject?3. 如何设计一个由多种资产、生物等组成的关卡?4. 在哪里放置特定角色的代码(例如生物、物品)?Unity 中“向 GameObject 添加 MonoBehaviour”…...

卷运维不如卷网络安全
最近发现很多从事运维的选择了辞职,重新规划自己的职业发展方向。运维工程师这个岗位在IT行业里面确实是处于最底层的,不管什么环节出现问题,基本都是运维背锅。背锅也就罢了,薪资水平也比不上别的岗位。 一般运维的薪资水平大多数…...

Digger PRO - Voxel enhanced terrains
资源链接在文末 Digger PRO 是一个简单但强大的工具,可以直接从 Unity 编辑器或游戏中创建天然洞穴和悬岩。会让你感觉自己手中握有一个体素地形,且毫无瑕疵。它实际上保持着最新、最快且可靠的 Unity 地形系统,并在你需要的地方无缝创建洞穴/悬岩峭壁网格。Digger 内…...
文字处理工具 word 2019 mac中文版改进功能
Microsoft Word 2019 是微软公司的文字处理软件,是 office 2019 套件中的一部分。它是一个功能强大、易于使用的工具,可以帮助用户创建各种类型的文档,包括信函、简历、报告、手册等。 Word 2019 提供了许多功能和改进,包括更好的…...

LeetCode 54. 螺旋矩阵
题目链接 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目解析 1、求出当前矩阵左上角的元素和右下角的元素。 2、根据这两个元素来确定我们需要遍历的具体位置。 3、当遍历完一圈的时候更新左上角元素和右下角元素。 细节: 当遍历最…...
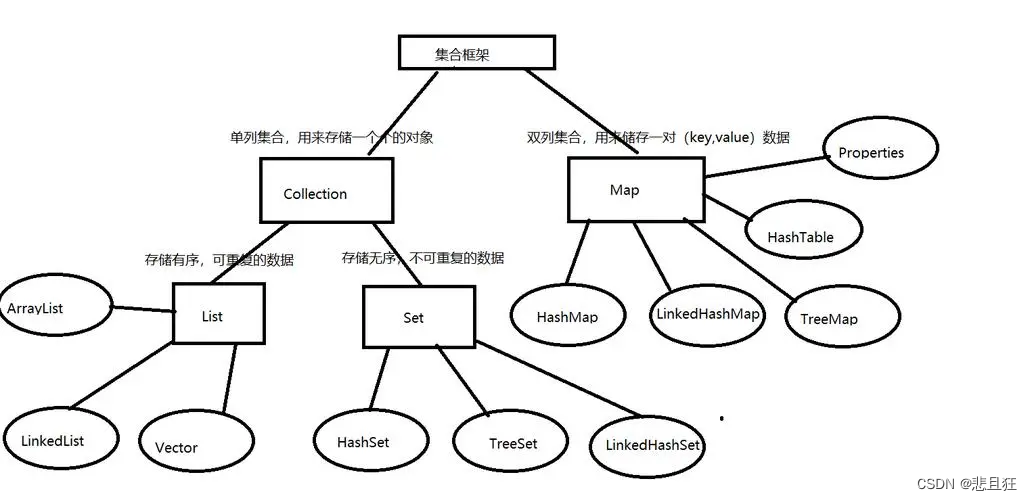
每天几道Java面试题:集合(第四天)
目录 第四幕 、第一场)大厦楼下门口第二场)大门口 友情提醒 背面试题很枯燥,加入一些戏剧场景故事人物来加深记忆。PS:点击文章目录可直接跳转到文章指定位置。 第四幕 、 第一场)大厦楼下门口 【面试者老王,门卫甲…...
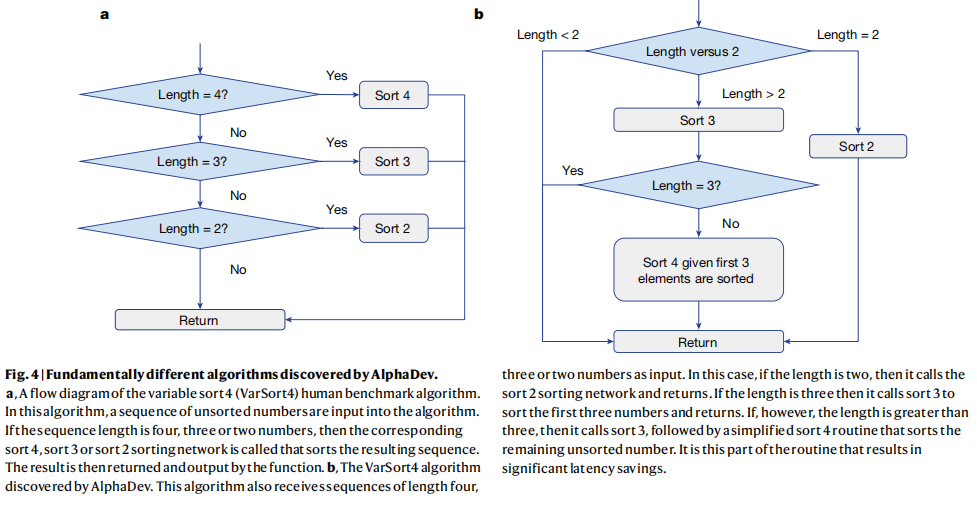
【论文解读】Faster sorting algorithm
一、简要介绍 基本的算法,如排序或哈希,在任何一天都被使用数万亿次。随着对计算需求的增长,这些算法的性能变得至关重要。尽管在过去的2年中已经取得了显著的进展,但进一步改进这些现有的算法路线的有效性对人类科学家和计算方法…...
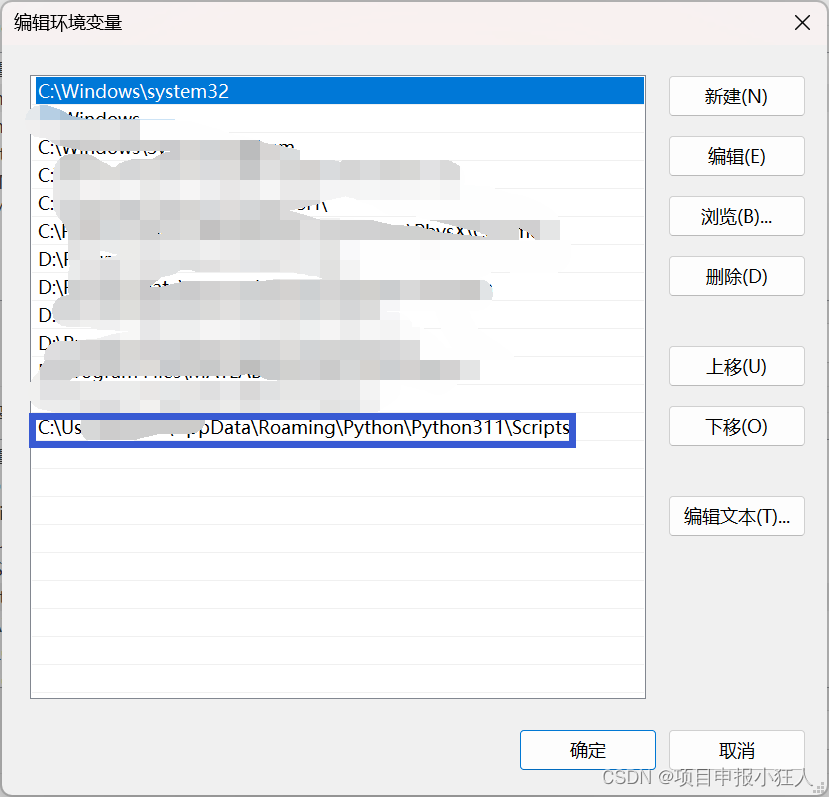
latexocr安装过程中遇到的问题解决办法
环境要求:需要Python版本3.7,并安装相应依赖文件 具体的详细安装步骤可见我上次写的博文:Mathpix替代者|科研人必备公式识别插件|latexocr安装教程 ‘latexocr‘ 不是内部或外部命令,也不是可运行的程序或批处理文件的相关解决办…...

如何判断linux 文件(或lib)是由uclibc还是glibc编译出来的?
工作中使用的编译环境有2套编译器,一个是glibc,一个是uclibc。 有些项目使用的glibc编译的lib,和使用uclibc编译的工程,在一起就会出现reference的编译错误如下: 那和如何来判断一个文件是由哪个编译器编译的呢&#…...

WorkPlus | 好用、专业、安全的局域网即时通讯及协同办公平台
自国家于2022年发布的《关于加强数字政府建设的指导意见》以来,我国数字政府建设已经迈入了一个全新的里程碑,迎来了全面改革和深化升级的全新阶段。 WorkPlus作为自主可控、可信安全、专属定制的数字化平台,扮演着政务机关、政府单位以及各…...

ARM Linux DIY(十二)NES 游戏
文章目录 前言交叉编译工具链使能 Cnes 游戏模拟器移植游戏手柄调试 前言 很多小伙伴为了不让自己的 V3s 吃灰,进而将其打造成游戏机。 我们 DIY 的板子具备屏幕、扬声器、USB Host(可以接游戏手柄),当然也要凑一凑热闹。 交叉编…...

MOEA算法的背景知识
MOEA算法 多目标进化算法优化MOEA工作原理举个例子 为什么单一策略可能会导致种群中的个体过于相似?种群在MOEA里面做什么?举例说明 多目标进化算法优化MOEA Multi-objective evolutionary algorithm optimization (MOEA) 多目标进化算法优化࿰…...
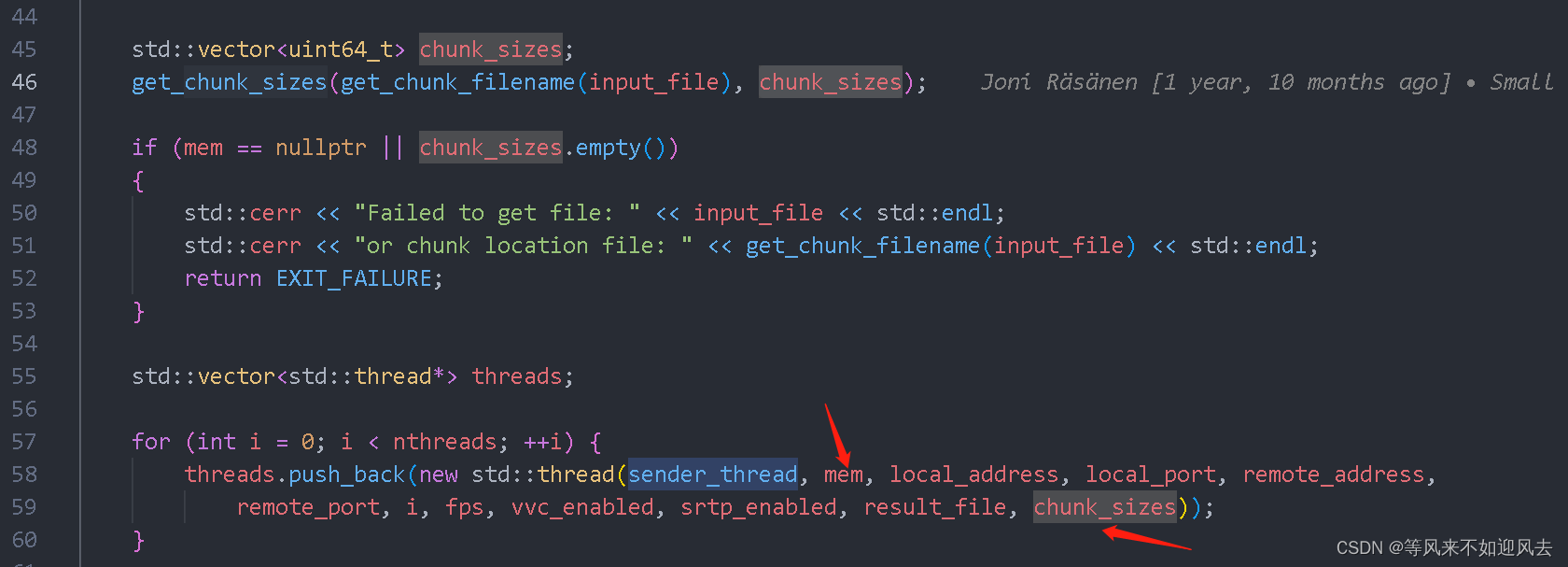
【rtp-benchmarks】读取本地文件基于uvgRtp实现多线程发送
input 文件做内存映射 : get_mem D:\XTRANS\soup\uvg-rtp-dev\rtp-benchmarks\util\util.cc 文件中读取chunksize 到 vector 里作为chunks 创建多个线程进行发送 std::vector<std::thread*> threads;...
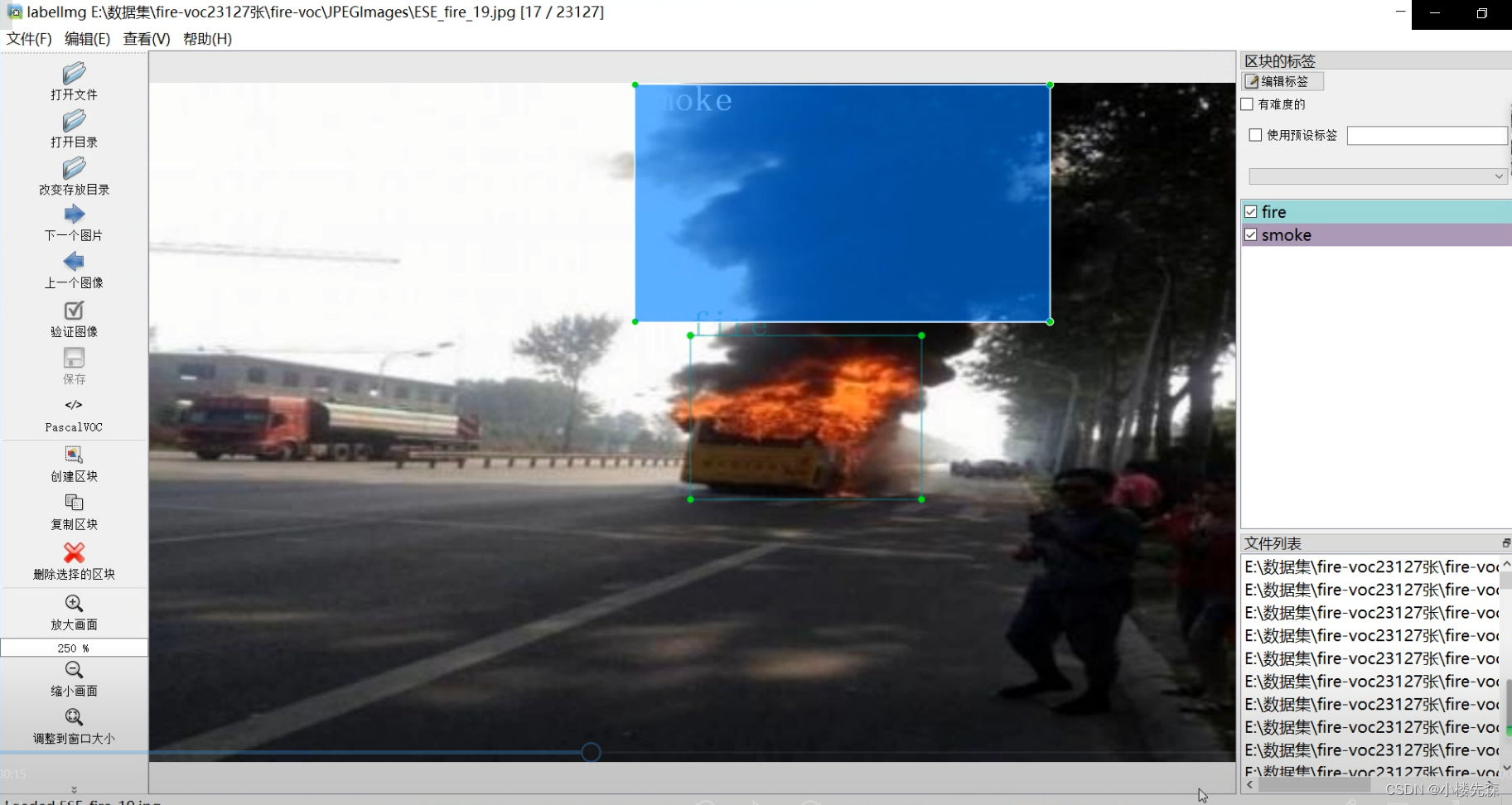
fire-voc 火光 烟火 火灾 目标检测数据集
一年中最容易引发火灾的季节是在冬季,主要原因有这样几点。 1、秋冬季节,随着用火、用电、用气增加,加上天气干燥,棉花、木材 、衣物等物体内含有的水分也较低。2、秋冬季风力较大,一旦有火苗冒起就很容易随风蔓延,是火灾的高发期。3、春季也是火灾多发季节&#x…...

【力扣1462】课程表(拓扑排序+bitset优化到O(n))
题目描述: 你总共需要上 numCourses 门课,课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ,其中 prerequisites[i] [ai, bi] 表示如果你想选 bi 课程,你 必须 先选 ai 课程。 有的课会有直接的先修课程&am…...
【AI】机器学习——支持向量机(非线性及分析)
5. 支持向量机(线性SVM) 文章目录 5.4 非线性可分SVM5.4.1 非线性可分问题处理思路核技巧核函数特点 核函数作用于SVM 5.4.2 正定核函数由 K ( x , z ) K(x,z) K(x,z) 构造 H \mathcal{H} H 空间步骤 常用核函数 5.5 SVM参数求解算法5.6 SVM与线性模型关系 5.4 非线性可分SVM …...
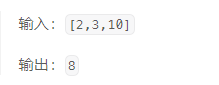
2023-09-20 LeetCode每日一题(拿硬币)
2023-09-20每日一题 一、题目编号 LCP 06. 拿硬币二、题目链接 点击跳转到题目位置 三、题目描述 桌上有 n 堆力扣币,每堆的数量保存在数组 coins 中。我们每次可以选择任意一堆,拿走其中的一枚或者两枚,求拿完所有力扣币的最少次数。 示…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
