基于Levenberg-Marquardt算法的声源定位matlab仿真
目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
5.算法完整程序工程
1.算法运行效果图预览
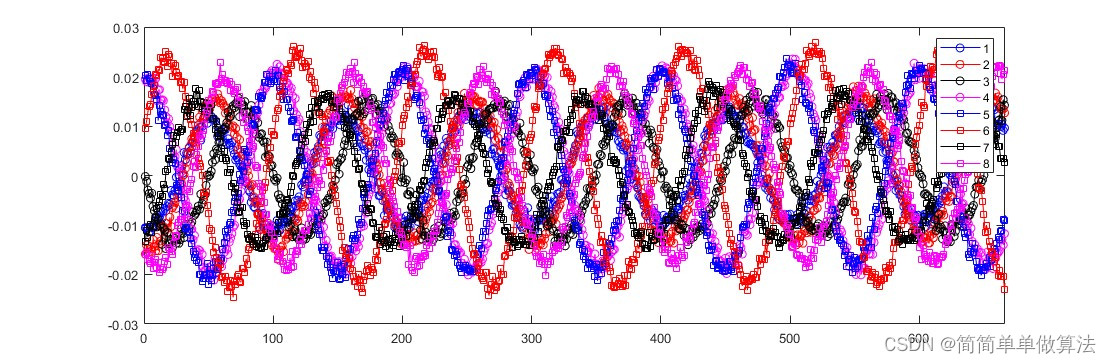
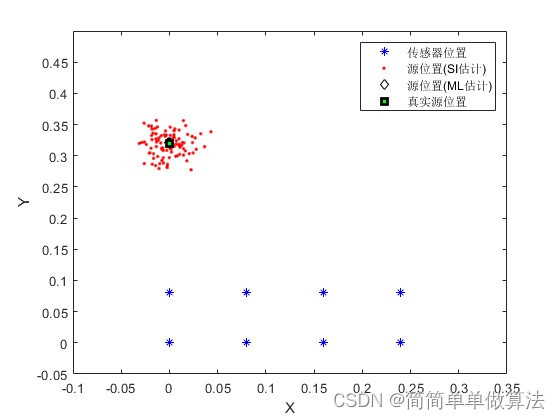
2.算法运行软件版本
matlab2022a
3.部分核心程序
....................................................................
%ML
if (bML==1)varxs_ML=var(bias_Xs_ML(:,1)); varys_ML=var(bias_Xs_ML(:,2)); varrs_ML=var(bias_Rs_ML); varbear_ML=var(bias_bearing_ML);vect_var_ML=[varxs_ML;varys_ML;varrs_ML;varbear_ML];
end% Calculate second moment (RMS)= sqrt {E[a^2]} = sqrt {mean^2 + variance}
% -----------------------------------------------------
rmsxs_SI=sqrt(mean(bias_Xs_SI(:,1)).^2+varxs_SI);
rmsys_SI=sqrt(mean(bias_Xs_SI(:,2)).^2+varys_SI);
rmsrs_SI=sqrt(mean(bias_Rs_SI).^2+varrs_SI);
rmsbear_SI=sqrt(mean(bias_bearing_SI).^2+varbear_SI);vect_rms_SI=[rmsxs_SI;rmsys_SI;rmsrs_SI;rmsbear_SI];%ML
if (bML==1) rmsxs_ML=sqrt(mean(bias_Xs_ML(:,1)).^2+varxs_ML); rmsys_ML=sqrt(mean(bias_Xs_ML(:,2)).^2+varys_ML); rmsrs_ML=sqrt(mean(bias_Rs_ML).^2+varrs_ML); rmsbear_ML=sqrt(mean(bias_bearing_ML).^2+varbear_ML);vect_rms_ML=[rmsxs_ML;rmsys_ML;rmsrs_ML;rmsbear_ML];
end
......................................................................
fisher=jacobian'*inv(cov_mat)*jacobian;crlb= trace(fisher^-1); % compare with MSE of Rs% -----------------------------------------------------
% Generate Plots
% -----------------------------------------------------% hfig1=figure;
if (bML==1)
plot(xi, yi,'b*',Xs_SI(:,1), Xs_SI(:,2),'r.',Xs_ML(:,1), Xs_ML(:,2), 'kd'); % plot both SI and ML
hold on
plot(xs_src_actual, ys_src_actual,'rs','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g','MarkerSize',6); % plot both SI and MLelse
plot(xi, yi,'bv', xs_src_actual, ys_src_actual, 'r^', Xs_SI(:,1), Xs_SI(:,2), 'mo'); % plot just SI only
endif (bML==1)
legend('传感器位置', '源位置(SI估计)','源位置(ML估计)','真实源位置' );
else
legend('传感器位置', '真实源位置', '源位置(SI估计)');
endxlabel('X');
ylabel('Y');axis([-0.1,0.35,-0.05,0.5]);
36_004m4.算法理论概述
Levenberg-Marquardt 算法是求非线性最小二乘问题的一种优化算法。它在不需要二阶导数信息的情况下,仍然可以取得相当不错的优化效果。它对于具有强非线性性和高维度的问题,尤为适用。
Levenberg-Marquardt 算法是在高斯-牛顿法和梯度下降法之间寻求一种折中的优化算法。在每一步迭代中,它使用高斯-牛顿法的近似 Hessian 矩阵,但是加上一个引入松弛性质的调节因子,这样可以大幅度减少病态问题的发生。同时,Levenberg-Marquardt 算法也采用了梯度下降法的思想,在 Hessian 矩阵无法更新或者接近于无法更新的时候,使用梯度下降法继续迭代。
Levenberg-Marquardt 算法的本质是在求解非线性最小二乘问题中,将误差平方和作为代价函数,找到一种参数的集合,使得该代价函数最小。在每一步迭代中,它通过计算代价函数的一阶导数和二阶导数,更新参数的值。对于 Hessian 矩阵接近奇异矩阵或者代价函数停滞不前的情况,它通过调节因子来提高二阶导数的稳定性。同时,为了防止过拟合,Levenberg-Marquardt 算法还采用了正则化的方法,用来处理噪声和异常点。
声源定位是一种通过声音来确定其来源的技术。它广泛应用于语音识别、音频信号处理、机器人听觉、生物医学影像处理等领域。
在声源定位中,基于Levenberg-Marquardt算法是一种常用的优化方法,它主要用于求解非线性最小二乘问题。其基本原理是通过迭代来优化目标函数,直到达到最优解。
一、Levenberg-Marquardt算法的基本原理
Levenberg-Marquardt算法是一种迭代方法,用于求解非线性最小二乘问题,它通过最小化目标函数与已知数据之间的差异来定位声源。
其基本原理是将目标函数与已知数据之间的差异定义为残差,然后通过迭代来最小化残差。在每次迭代中,根据当前估计的参数值,计算出残差的梯度,然后使用该梯度来更新参数。
Levenberg-Marquardt算法的优点在于它能够处理非线性问题,同时避免了大量的矩阵计算,因此适用于实时声源定位系统。
其基本原理如下:

在迭代过程中,需要根据具体情况调整阻尼因子λ的值,以确保算法的收敛速度和稳定性。一般来说,如果迭代次数过多或者收敛速度较慢,可以增大λ的值;如果迭代次数过少或者收敛速度过快,可以减小λ的值。
二、Levenberg-Marquardt算法的应用
在声源定位中,Levenberg-Marquardt算法可以应用于多种场景,例如:
- 语音识别:通过分析语音信号的特征,利用Levenberg-Marquardt算法确定说话人的位置;
- 音频信号处理:对音频信号进行特征提取和模型训练,再利用Levenberg-Marquardt算法优化模型参数;
- 机器人听觉:通过分析声音信号的空间分布,利用Levenberg-Marquardt算法确定声源在机器人坐标系下的位置;
- 生物医学影像处理:通过对医学影像进行分析和处理,利用Levenberg-Marquardt算法确定病灶的位置和大小。
总之,Levenberg-Marquardt算法在声源定位领域中具有广泛的应用前景。然而,在实际应用中还需要考虑其他因素,如噪声干扰、多径传播、信号衰减等,这些因素可能会影响定位精度和稳定性。因此,在实际应用中需要结合具体场景进行算法优化和实验验证。
5.算法完整程序工程
OOOOO
OOO
O
相关文章:

基于Levenberg-Marquardt算法的声源定位matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 .................................................................... %ML if (bML1)varxs…...

vscode的Emmet语法失效
解决方案:设置 -> 搜索Emmet -> 勾选 Emmet:Trigger Expansion On Tab和Emmet: Use Inline Completions -> 重启 注:Emmet语法是vscode自带的语法,可以快速生成HTML结构/CSS样式/格式化语法 Emmet语法 参考:关于vscode使…...

堆排序(大根堆)
堆的定义如下,n个关键字序列[1...n]称为堆,当且仅当满足: a(i)>a(2i)且a(i)>a(2i1) 这个为大根堆 a(i)<a(2i)且a(i)<a(2i 1) 这个为小根堆 通过建堆得到大根堆 大根堆 87,45,78,32,17,65,53,9 可以看成 …...
Mybatis学习笔记3 在Web中应用Mybatis
Mybatis学习笔记2 增删改查及核心配置文件详解_biubiubiu0706的博客-CSDN博客 技术栈:HTMLServletMybatis 学习目标: 掌握mybatis在web应用中如何使用 Mybatis三大对对象的作用域和生命周期 关于Mybatis中三大对象的作用域和生命周期、 官网说明 ThreadLocal原理及使用 巩…...

软件测试之功能测试详解
一、功能测试概述 1)功能测试就是对产品的各功能进行验证,根据功能测试用例,逐项测试,检查产品是否达到用户要求的功能。 2)功能测试,根据产品特性、操作描述和用户方案,测试一个产品的特性和…...

javascript选取元素的范围,可以包含父级,也可以不包含父级
//函数可以选取元素的范围,对于要选取文本的非常方便,或选取特定的子节点 function getRange(element){//判断是否支持range范围选取var supdocument.implementation.hasFeature("Range","2.0");var also(typeof document.createRan…...

QGIS怎么修改源代码?持续更新...
修改配置文件保存位置 修改目的:放着和本地安装的其他QGIS共用一份配置文件 修改文件:core/qgsuserprofilemanager.cpp 修改位置:第37行 return basePath QDir::separator() "my_profiles";修改完毕后,再次生成一下…...
dev board sig技术文章:轻量系统适配ARM架构芯片平台
摘要:本文简单介绍OpenHarmony轻量系统移植,会分多篇 适合群体:想自己动手移植OpenHarmony轻量系统的朋友 开始尝试讲解一下系统的移植,主要是轻量系统,也可能会顺便讲下L1移植。 1.1移植类型 OpenHarmony轻量系统的…...

MyBatis之增删查改功能
文章目录 一、创建各种类二、MyBatis的各种功能 1、查询<select>2、增加<insert>3、修改<update>4、删除<delete>三、总结 前言 在MyBatis项目中编写代码实现对MySql数据库的增删查改 一、创建各种类 1、在Java包的mapper文件下创建一个接口 我创建…...

Leetcode算法入门与数组丨5. 数组二分查找
文章目录 1 二分查找算法2 二分查找细节3 二分查找两种思路3.1 直接法3.2 排除法 1 二分查找算法 二分查找算法是一种常用的查找算法,也被称为折半查找算法。它适用于有序数组的查找,并通过将待查找区间不断缩小一半的方式来快速定位目标值。 算法思想…...
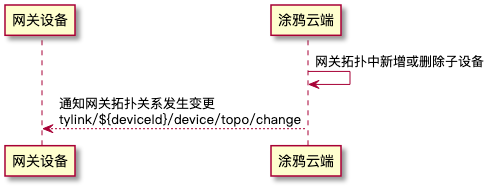
拓扑关系如何管理?
在设备对接涂鸦的云端过程中,一部分设备由于自身资源或硬件配置,无法直接连接云端。而是需要通过网关进行中转,由网关代理实现和云端进行数据交互,间接实现设备接入云端。这样的设备也称为子设备。 要想实现网关代理子设备接入云…...

vue的由来、vue教程和M-V-VM架构思想、vue的使用、nodejs
vue vue的由来 vue教程和M-V-VM架构思想 vue的初步简单使用 nodejs vue的由来 # 1 HTML(5)、CSS(3)、JavaScript(ES5、ES6、ES11):编写一个个的页面 -> 给后端(PHP、Python、Go、Java) -> 后端嵌入模板语法 -> 后端渲染完数据 -> 返回数据给前端 ->…...

课程表 循环依赖 拓扑排序 go语言
学会拓扑排序题目的基本解法 res数组 记录上课顺序g 记录学了课程i 能解锁的课程jindeg 记录每个课程的入度q 记录入度为0的课程 for循环q去解放其他课程 本题来自力扣课程表 func findOrder(numCourses int, prerequisites [][]int) []int {res : []int{}//建一个二维数组记…...

【红包雨接口设计】
一、服务器地址 http://rb.atguigu.cn 二、公共请求头参数 参数名称类型是否必选描述tokenString是用户唯一标识 备注:为了方便我们今天演示,服务端接受所有token。 三、接口 1. 创建红包雨 请求方式:GET请求地址:/api/v1/se…...

SSL证书到期更换证书会影响排名吗?
在现代的数字化时代,网络安全和用户体验成为了网站运营商和开发者们需要高度关注的问题。SSL证书作为一种重要的安全协议,对网站的安全性和用户信任起着至关重要的作用。然而,随着SSL证书的有效期限届满,许多网站运营商面临着更换…...

前端常用库之-JavaScript工具库lodash
文章目录 前端常用库之-JavaScript工具库lodash一、什么是lodash二、安装三、lodash使用Lodash 的 pick() 函数介绍和使用react 实例demo:pick结合...展开运算符(spread operator) 前端常用库之-JavaScript工具库lodash 一、什么是lodash 官网: https:…...
)
Linux- execve()
execve() 是 Linux/UNIX 中的 exec 函数家族中的一个,它允许进程执行一个新的程序。具体地,execve() 替换当前进程的映像为新的程序映像。 函数原型如下: int execve(const char *pathname, char *const argv[], char *const envp[]);pathn…...
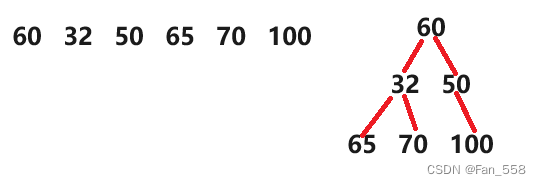
007 数据结构_堆——“C”
前言 本文将会向您介绍关于堆Heap的实现 具体步骤 tips:本文具体步骤的顺序并不是源代码的顺序 typedef int HPDataType; typedef struct Heap {HPDataType* _a;int _size;int _capacity; }Heap;初始化 void HeapCreate(Heap* hp, HPDataType* a, int n) {hp-&…...
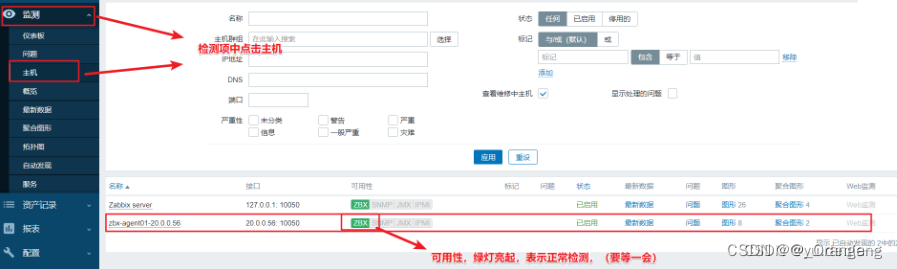
zabbix的原理与安装
一、Zabbix介绍 1、zabbix 是什么? zabbix是一个开源的IT基础监控软件,能实时监控网络服务,服务器和网络设备的状态,如网络使用,CPU负载、磁盘空间等,主要是包括数据的收集、报警和通知的可视化界面zabbi…...
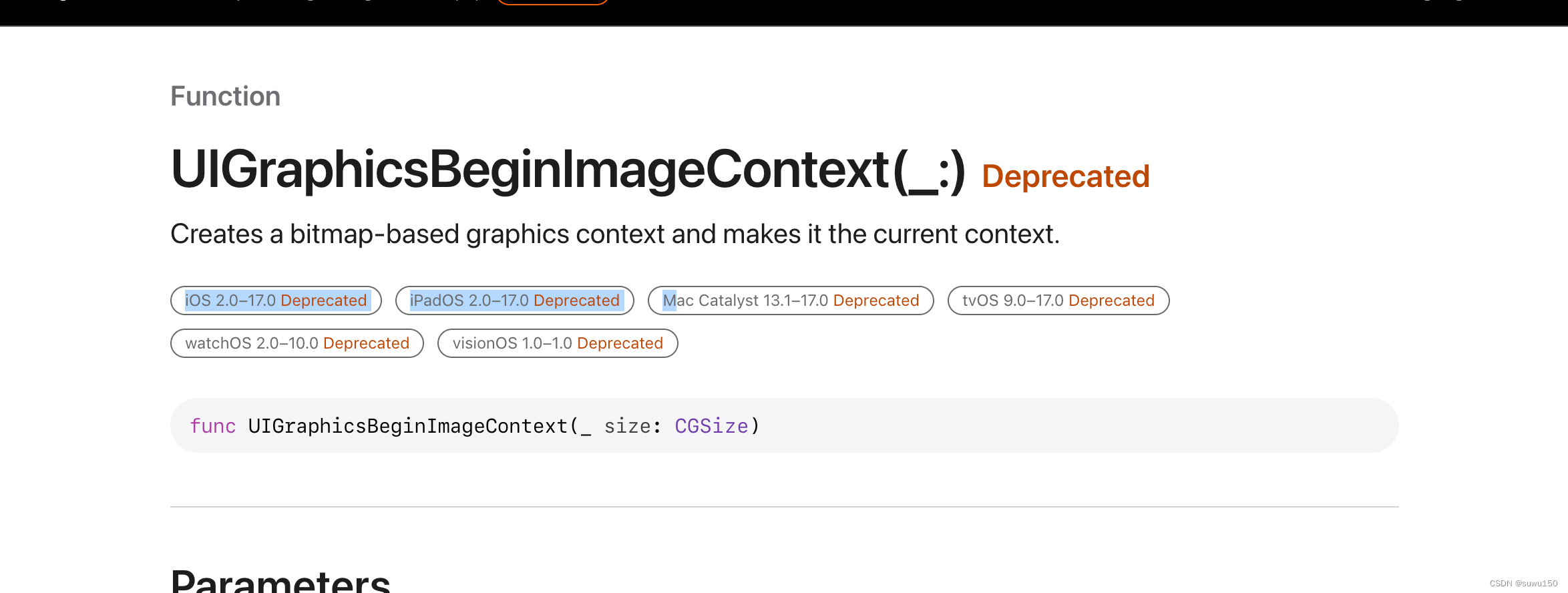
ReactNative中升级IOS 17版本Crash解决
ReactNative中升级IOS 17版本Crash解决 ReactNative中升级IOS 17版本Crash解决一、问题描述二、原因分析三、解决方案决策3.1 设置宽高为非零值3.2 使用新的UIGraphicsImageRenderer替换就版本的UIGraphicsBeginImageContext 四、可能使用到该API的三方库4.1 react-native-fast…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
