[python 刷题] 128 Longest Consecutive Sequence
[python 刷题] 128 Longest Consecutive Sequence
题目:
Given an unsorted array of integers
nums, return the length of the longest consecutive elements sequence.You must write an algorithm that runs in
O(n)time.
这题给了一个没有排序的数组,并且要求找出最长的连续序列
最简单的方式其实还是排序,不过题目中要求时间复杂度为 O ( n ) O(n) O(n),而排序的时间复杂度为 O ( n l o g ( n ) ) O(n log(n)) O(nlog(n))
Union Find 也可以用来解这题,它的时间复杂度是 amortized linear,不过这个问题的话有一个 linear 的解。
以 [100,4,200,1,3,2] 为例,假设有一个无限延长的 x 轴,所有的点在 x 轴上看起来是这个样子的:

这个情况下就比较清楚的可以看到哪个点在哪个 cluster 里,在实际的实现中,可以用一个 set 去存储所有出现的值,每次将值存入 cluster 中,都可以检查一下当前值是否是 cluster 的最小值,如果是的话,查看当前 cluster 的长度
代码如下:
class Solution:def longestConsecutive(self, nums: List[int]) -> int:num_set = set(nums)max_len = 0for num in num_set:if (num - 1) in num_set:continuelocal_max = 1right = num + 1while right in num_set:local_max += 1right += 1max_len = max(max_len, local_max)return max_len
整体时间复杂度的分析:
创建 set 的时间复杂度为 O ( n ) O(n) O(n)
第一个 for 循环的时间复杂度为 O ( n ) O(n) O(n),
查询当前值是否存在与 set 的时间复杂度为 O ( 1 ) O(1) O(1)
第二个循环 while 在最差的情况下会跑 O ( n ) O(n) O(n) 次,但是因为有 if,的检查,所以这个情况最坏只会跑一次,而 O ( n + n ) O(n + n) O(n+n) 在大 O 里面依旧是 O ( n ) O(n) O(n),所以整体的时间复杂度为 O ( n ) O(n) O(n)
相关文章:

[python 刷题] 128 Longest Consecutive Sequence
[python 刷题] 128 Longest Consecutive Sequence 题目: Given an unsorted array of integers nums, return the length of the longest consecutive elements sequence. You must write an algorithm that runs in O(n) time. 这题给了一个没有排序的数组&#x…...

SpringMVC之JSON数据返回与异常处理机制
目录 一.SpringMVC的JSON数据返回 1.导入Maven依赖 2.配置spring-mvc.xml 3.ResponseBody注解的使用 3.1案例演示 1.List集合转JSON 2.Map集合转JSON 3.返回指定格式String 4. ResponseBody用法 5.Jackson 5.1介绍 5.2常用注解 二.异常处理机制 1.为什么要全局异常处…...

【第四阶段】kotlin语言的定义类和field关键字学习
1.普通成员变量背后隐士代码 为什么在kotlin中是private 可以直接调用,隐式代码如下 package Kotlin.Stage4class Test54{var name"kotlin"/*背后做的事NotNullprivate String name"kotlin";public void setName(NotNull String name){this.na…...

OpenResty使用漏桶算法实现限流
前言 其它项目组需要调用接口,添加接口限流,防止项目被狂掉宕机。生产用了openresty,所以在openresty上添加按接口限流,同时,需按照不同接口有不同的限流规则,使用openresty中内置的漏桶算法方式限流。 漏…...

Activiti源码跟踪之模型Model操作
Activiti源码跟踪之模型Model操作 模型model设计到的表ACT_RE_MODEL、ACT_GE_BYTEARRAY ACT_RE_MODEL表结构: CREATE TABLE ACT_RE_MODEL (ID_ varchar(64) COLLATE utf8_bin NOT NULL,REV_ int(11) DEFAULT NULL,NAME_ varchar(255) COLLATE utf8_bin DEFAULT N…...
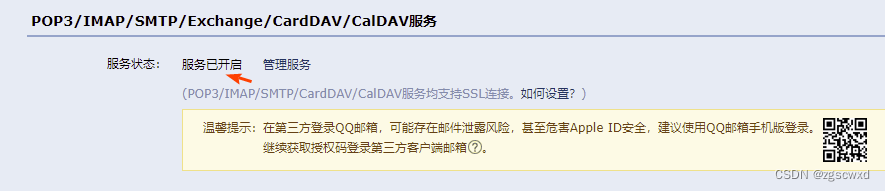
C#-WinForm-发送邮件
登录QQ邮箱——设置——开启“POP3/SMTP服务” 登陆QQ邮箱→打开设置→开启“POP3/SMTP服务”,获取“授权码” 简单总结一下: 1、使用SmtpClient发送电子邮件是很简单的,只要正确创建了MailMessage对象和SmtpClient就可以很容易的发送出去电…...

Springboot整合jdbc和Mybatis
目录 整合jdbc 1. 新建项目 2. 编写yaml配置文件连接数据库 3. 测试类 使用原生的jdbcTemplate进行访问测试 使用Druid连接池 1. 添加类型 2. 初始化连接池 3. 编写config类 配置Druid数据源监视 整合Mybatis 1. 导入依赖 2. 编写mapper接口 3. 编写实体类 4. 编…...
日常生活中的常用命令及操作
目录 一、Windows11 中查看网卡名称 及ip地址 二、查看硬件的详细信息 三、查看显卡声卡详细信息及厂商 四、C盘清理 第一步 输入wini 开启Windows设置主界面 第二步 存储中还有一个叫存储感知的功能 第三步 更改新内容的保存位置 第四步 怕误C盘内的东西可以 查看详细的…...

【C++杂货铺】国庆中秋特辑——多态由浅入深详细总结
文章目录 一、多态的概念二、多态的定义及实现2.1 多态的构成条件2.2 虚函数2.3 虚函数的重写2.4 虚函数重写的两个例外2.4.1 协变(基类与派生类虚函数返回值类型不同)2.4.2 析构函数的重写(基类与派生类析构函数的名字不同) 2.5 …...

MongoDB基础详解
一、MongoDB概述 MongoDB 是一个基于 分布式文件存储 的开源 NoSQL 数据库系统,由 C 编写的。MongoDB 提供了 面向文档 的存储方式,操作起来比较简单和容易,支持“无模式”的数据建模,可以存储比较复杂的数据类型,是一…...

解锁前端Vue3宝藏级资料 第五章 Vue 组件应用 4 ( provide 和 inject )
5.5 provide 和 inject 前面的知识告诉我们vue中组件之间传递值需要使用props来完成,但是props也有一定局限性。这个时候在vue3中还有另外的解决方法。那就是使用 provide 和 inject 允许父组件将数据传递给所有后代组件,而不管组件层次结构有多深。你要…...
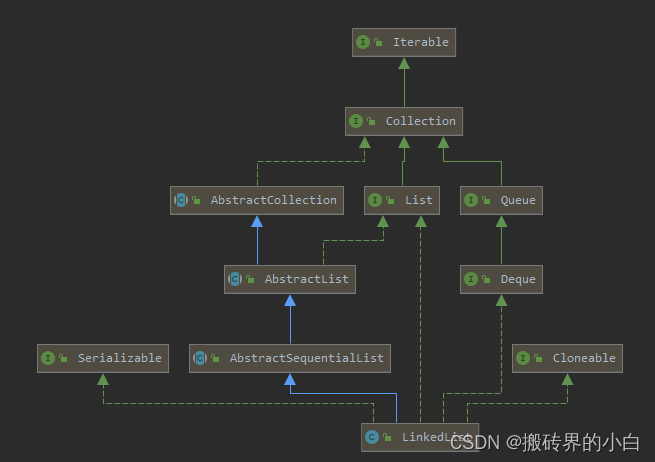
【List篇】LinkedList 详解
目录 成员变量属性构造方法add(), 插入节点方法remove(), 删除元素方法set(), 修改节点元素方法get(), 取元素方法ArrayList 与 LinkedList的区别Java中的LinkedList是一种实现了List接口的 双向链表数据结构。链表是由一系列 节点(Node)组成的,每个节点包含了指向 上一个…...

推动统一供应链“度量衡”,上汽大通突破传统拥抱SaaS生态
中国汽车市场规模已连续14年位居世界第一,目前占世界汽车份额31%。近年来,物联网、人工智能、电池等技术的快速发展,也为中国从汽车大国逐步迈向汽车强国注入巨大动力。在新一轮的汽车产业变革中,构建一个更智能、更高效协同的供应…...
10.9-BLE 入门笔记之GAP)
蓝牙核心规范(V5.4)10.9-BLE 入门笔记之GAP
1.概述 蓝牙核心规范的通用访问配置文件(GAP)部分定义了与设备发现和在两个设备之间建立连接有关的过程。如何执行数据的基本无连接通信、如何使用周期性广播(参见 PADVB-LE Periodic Advertising Broadcast)以及如何设置等时通信(参见 LE BIS和LE CIS - Isochronous Com…...

nginx 配置 ssl
1.1 Nginx如果未开启SSL模块,配置Https时提示错误 原因也很简单,nginx缺少http_ssl_module模块,编译安装的时候带上--with-http_ssl_module配置就行了,但是现在的情况是我的nginx已经安装过了,怎么添加模块࿰…...
家居设计软件Live Home 3D Pro mac中文版特点介绍
Live Home 3D Pro mac是一款专业的3D家居设计软件,可以帮助用户轻松创建和设计家居平面图和3D模型,并进行渲染和虚拟漫游。 Live Home 3D Pro mac软件特点 1. 界面友好:Live Home 3D Pro的界面友好,操作简单方便…...

OkHttp - 现代应用网络的方式
官网:Overview - OkHttp HTTP is the way modern applications network. It’s how we exchange data & media. Doing HTTP efficiently makes your stuff load faster and saves bandwidth. OkHttp is an HTTP client that’s efficient by default: HTTP/2 s…...
SpringBoot3基础:最简项目示例
说明 本文建立一个最基本的SpringBoot3项目,依赖项仅包含 spring-web(SpringMVC)。 备注:SpringBoot3需要JDK17支持,配置方法参考: SpringBoot3项目中配置JDK17 项目结构图示 POM <?xml version&qu…...

flex:1详解,以及flex:1和flex:auto的区别
什么是flex:1? 在css中,我们经常可以看到这样的写法: .box {display: flex; }.item {flex: 1; }这里的flex:1相当于flex: 1 1 0%,它是一个简写属性,表示项目(flex item)在弹性容器…...

在VMware虚拟机中固定CentOS系统ip(使用桥接模式)
目录 一、前置说明二、前置准备2.1、切换虚拟机网络为桥接模式2.2、查看本机网络信息 三、配置CentOS系统IP3.1、进入系统输入ip addr 查看本机网络配置名称3.2、查看网络配置目录,网络配置文件名称3.3、修改网络配置文件 ifcfg-ens33 固定IP3.4、重启网络 一、前置…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...
