C++ - AVL树实现(下篇)- 调试小技巧
前言
本博客是 AVL树的下篇,上篇请看:C++ - AVL 树 介绍 和 实现 (上篇)_chihiro1122的博客-CSDN博客
上篇当中写插入操作,和其中涉及的 旋转等等细节,还有AVL树的大体框架。
调试小技巧
条件断点
在大项目当中,如果发生了程序的错误,崩溃的异常情况,那么因为项目过大,很多时候我们不能一步步去调试,这样非常的麻烦而且不现实。
在VS studio 当中,除了支持逐语句调试之外,还支持 条件调试,就是在某一个断点处,写上一句条件判别式,也就是表达式,可以设置当中这个 表达式为 false 或者 true 的时候,在此处语句停下来:
当我们右键做左边一列的(断点列),就会出现下图当中的 内容:
 此时我们可以选择插入条件断点:
此时我们可以选择插入条件断点:
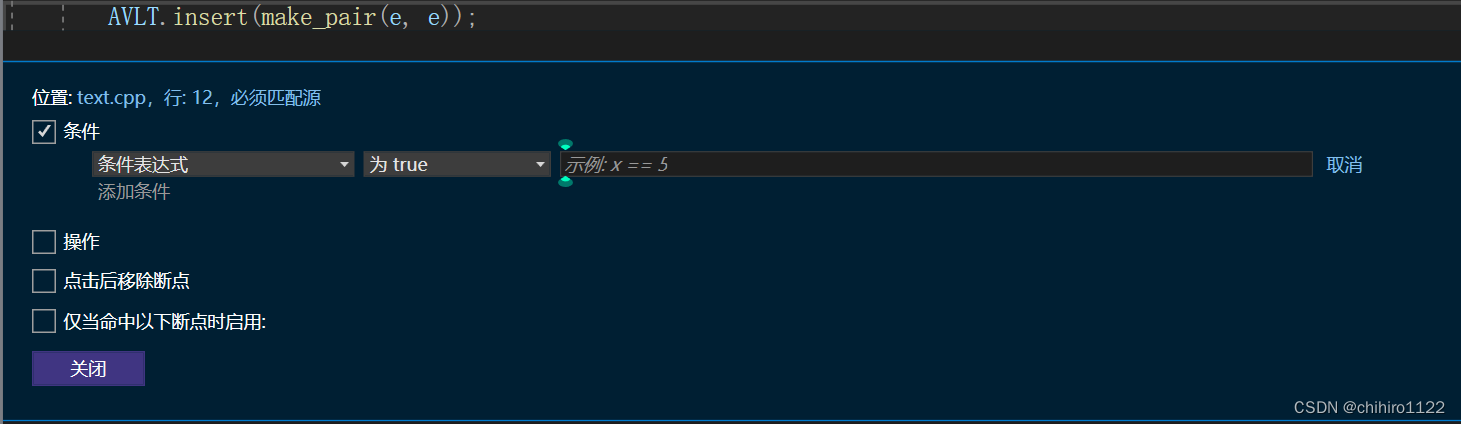
此时就会出现上述内容,上述内容就是 条件断点当中的条件设置,你可以在 最右边(在示例:x== 5 ) 这个位置处,写上你需要的条件表达式,然后还可以设置这个表达式为 true 或者为 false的时候停止执行。注意:是程序执行到 该断点处,才会进行判断表达式真假,才会进行停止或者继续执行的操作。
当然,此处不仅可以加条件表达式判断,还可以加一些 其他 判断方式:
可以自己下去研究。
其实还有一个方法和上述方法类似,我们可以在我们想要打断的地方,自己写一个 if()判断语句,然后在其中随便写上一段代码,打上断点,也可以实现和上述一眼的操作;注意:一定要在if()当中写上一行代码,空行是不能打断点的,会直接跳过:

如上所示,当 e 遍历的到 数组的 15 的时候,到达 if()就会停止。
这样,按下 f5 就会 执行到 e 遍历到 数组 15 这个元素之后停止,就不用再 手动调试到 15 这个元素位置了。
如果 这颗数非常大的话,那么上述方式还是非常好用的,加入在 15之前有 200 个需要插入的元素,手动一步步调试到 15 肯定是不现实的。
调用堆栈
可以在调试->窗口当中找到 调用堆栈这个窗口,当我们逐语句查看代码执行过程的时候,其中可能会调用多个函数,而每一个函数都有对应的函数栈帧,如果单独使用 f10 f11 来走的话,不好回溯;这时候我们可以在 调用堆栈这个窗口当中看到 从开始到现在,所调用函数的函数堆栈:
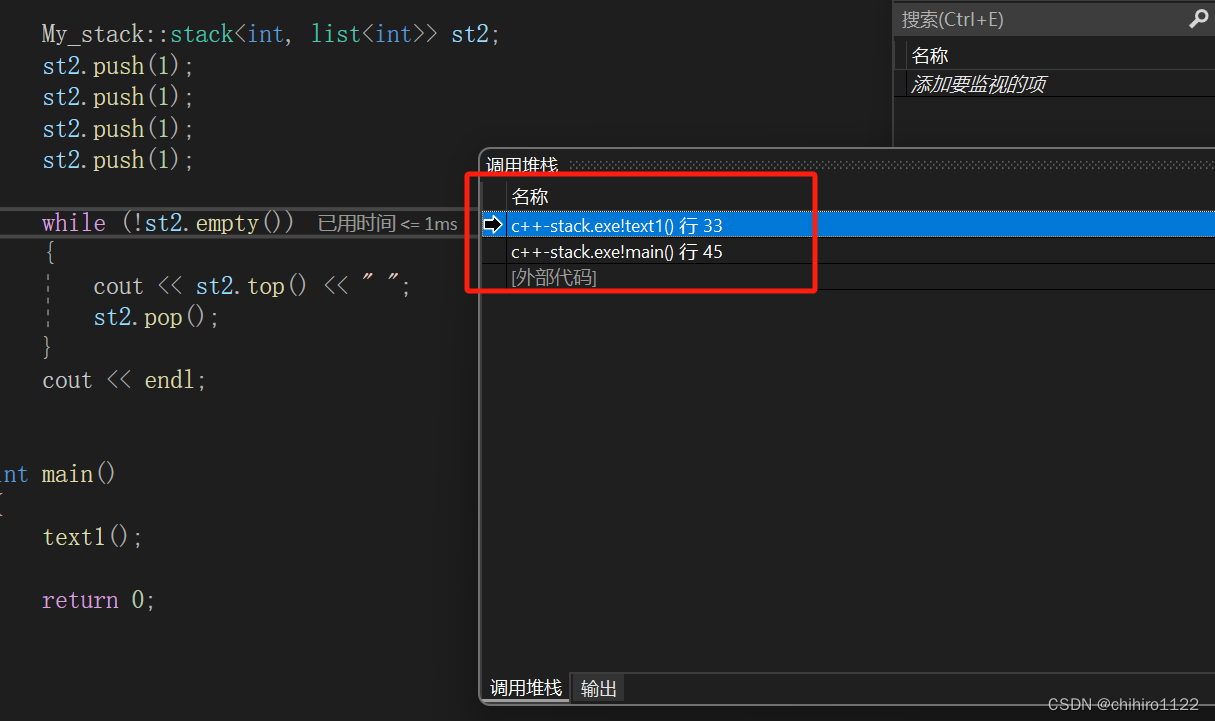
此时我们只需要点击一下其中某一个函数堆栈,就可以直接回溯到 这个函数当中进行执行。
写一些小程序来帮助我们判别一些规律性问题
比如在自己实现 AVL 树当中,我们不太可能一步就直接写到位,出错是大概率的事情,而且像AVL树这种规则复杂的数据结构,在调试起非常的麻烦,此时我们为了更好的调试,写一个小程序来帮助我们判断,每插入一个结点之后,这颗树还是不是一颗 AVL树。
AVL树
判断一颗AVL树是不是 平衡的
private:int Height(Node* root){if (root == nullptr)return 0;int HeightLeft = Height(root->_left);int HeightRight = Height(root->_right);return HeightLeft > HeightRight ? HeightLeft + 1 : HeightRight + 1;}// 判断是否是 平衡的bool isBalance(Node* root){if (root == nullptr)return;// 记录左右子树的高度int HeightLeft = Height(root->_left);int HeightRight = Height(root->_right);// 判断计算出来的 平衡因子是否和 该结点当中存储的是一样的if ((HeightLeft - HeightRight) != root->_bf){cout << "平衡因子出错: " << root->_kv.first << "->" << root->_bf << endl;}// 递归判断左右子树当中的结点return abs(HeightLeft - HeightRight) < 2 && isBalance(root->_left)&& isBalance(root->_right);}在外部函数当中调用不了 其中的成员,也就是调用不了 根结点指针,所以我们还是写一个接口:
public:int Height(){return Height(_root);}bool isBalance(){return isBalance(_root);}删除结点
AVL树的删除操作比 插入还要困难一些,但是大体上也是三个步骤:
- 按照搜索树的规则查找结点删除
- 更新平衡因子
- 判断平衡因子是否符合规则,不符合就要旋转
如下述例子:

假设现在要删除结点 3 ,在删除之前 2 的平衡因子是 0 ,3 是 2 的右孩子,当删除3 之后, 2 的平衡因子要 --。2 的平衡因子从 0 减到 -1 ,那么 2 的平衡因子 更新到 -1 ,在插入当中是需要网上更新父亲的平衡因子的,但是在上述例子的删除当中就不需要望山更新,因为 4 的左子树高度 在删除 3 之后,没有变化。
而相反,如果在删除之后,删除结点的父亲的平衡因子 更新到 0 ,在插入当中是不需要网上更新的,但是在插入当中,如果一个结点的平衡因子 更新到0 ,说明该结点的某一个子树肯定发生了高度变化,比如删除上述例子的 14 这个结点,那么 7 结点的平衡因子 就会从 -1 更新到 0。此时就需要往上沿着父亲更新结点。在往上更新过程当中,只要是更新为0 了,都要继续网上更新。
而如果对结点的平衡因子进行更新,和插入当中类似,判断是从 父亲结点左右孩子的那一边更新上来的,从那边上来,就代表有那边的 高度发生了变化,对应的进行修改就好了。
其实上述在查找删除,更新平衡因子都还好,主要是在判断是否需要旋转的条件才是麻烦的。
不能再像 插入当中判断 是否需要旋转一样 ,沿着更新父亲结点的平衡因子路径上,判断更新之后父亲结点的平衡因子是否合法。
因为在删除结点之后,不是在删除路径的一边子树当中去判断旋转,因为此时多出来的高度的子树来,某一个平衡因子不合法的结点的另一边子树当中。找到平衡因子不合法的结点还不够,还需要找到使得这个结点为根结点的子树不平衡的子树。当然,这种情况是双旋的情况,如果是单旋就还好,不过双旋的问题可能是要解决的。
关于删除细节在 《算法导论》或《数据结构-用面向对象方法与C++描述》殷人昆版。这两本书当中就有详细的介绍。
AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这
样可以保证查询时高效的时间复杂度,即O(log N)。
但是如果要对AVL树做一些结构修改的操作,非常麻烦,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。
但是,AVL树本来就为了方便我们快速查找数据的,当插入好了之后,AVL树构建好了,我们在查找数据的时候会非诚的方便。
所以,AVL树一般用于静态的存储数据,比如你在一开始就把数据以AVL树的结果构建好,那么之后尽量少更改数据,建议不更改其中的数据,那么AVL树在只是查找数据方便还是非常方便的。
而且,AVL虽然在旋转上看似很复杂,其实性能上没有太大消耗,在旋转当中,没有旋转,只是单纯的修改链接指针和 修改平衡因子,这些都是常数级别的 时间复杂度。
所以,AVL树只是看似复杂,但是实际在使用过程当中的效率还是挺高的,比如下述程序:
void text2()
{AVLTree<int, int> AVLT;vector<int> v;int N = 10000;v.reserve(10000);srand(time(0));// 开始计时int start = clock();for (int i = 0; i < N; i++){v.push_back(rand());}for (const auto& e : v){AVLT.insert(make_pair(e, e));//cout << "insert():" << e << "->" << AVLT.isBalance() << endl;}cout << AVLT.isBalance() << endl;int end = clock();cout << "用时: " << (double)(end - start)/ CLOCKS_PER_SEC << "s" << endl;
}如上述程序,使用clock ()函数来计算整个程序的执行时间。
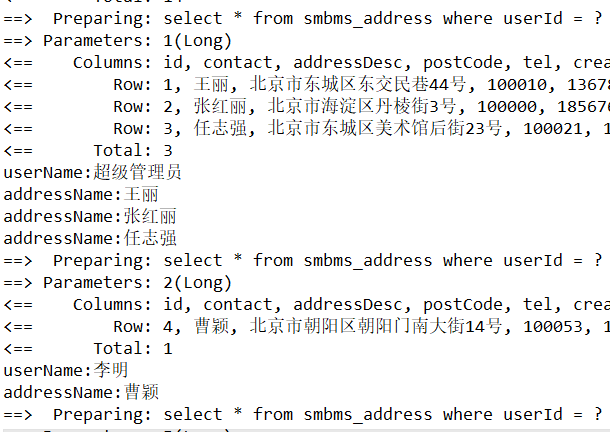
我们随机插入了 10000 个数据,而且还是用了 isBalance()这个效率不太好的递归函数去判断这个 树是不是 AVL树,输出:
1
用时: 0.006s可以看到,耗时 0.006 s。
相关文章:

C++ - AVL树实现(下篇)- 调试小技巧
前言 本博客是 AVL树的下篇,上篇请看:C - AVL 树 介绍 和 实现 (上篇)_chihiro1122的博客-CSDN博客 上篇当中写插入操作,和其中涉及的 旋转等等细节,还有AVL树的大体框架。 调试小技巧 条件断点 在大项目…...
Mybatis懒加载
懒加载是什么? 按需加载所需内容,当调用到关联的数据时才与数据库交互否则不交互,能大大提高数据库性能,并不是所有场景下使用懒加载都能提高效率。 Mybatis懒加载:resultMap里面的association、collection有延迟加载功…...

DSOX3012A是德科技keysight DSOX3012A示波器
181/2461/8938是德科技DSOX3012A(安捷伦)示波器 是德科技DSOX3012A(安捷伦)是InfiniiVision 3000 X系列中的双通道型号。这款可升级示波器采用突破性技术设计,提供卓越的性能和功能。其独特的5仪器合一设计为相同的预算提供了更大的范围。 是德科技DSOX3012A示波器…...

基于网络表示学习的 新闻推荐算法研究与系统实现
摘要 第1章绪论 新闻推荐通常是利用用户的阅读行为和习惯、阅读选择和爱好等信息,为 用户推荐新闻内容。新闻推荐能够减少用户在数量庞大数据信息中获取信息的 时间消耗,从而能够缓解“信息过载[7]”的难题。以文本为内容的新闻,和商品、 电影、短视频等推荐系统相比,新闻推…...
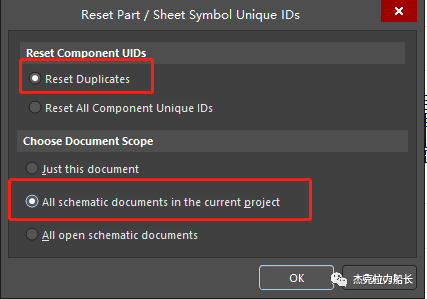
<Altium Designer> 将.DSN文件导入并转换成SchDoc文件
目录 01 使用向导方式导入.DSN 02 消除Unique Identifiers Errors 03 文章总结 大家好,这里是程序员杰克。一名平平无奇的嵌入式软件工程师。 本文主要是总结和分享将OrCAD Capture画的原理图文件(.DSN)导入到Altium Designer,转换成对应的原理图文件…...
视频定格合璧,批量剪辑轻松插入图片
大家好!想要将视频与图片完美融合吗?现在,我们为您推出一款强大的批量剪辑工具,让您能够轻松在图片中插入视频,让您的创作更加精彩动人! 首先,第一步我们要进入媒体梦工厂主页面,并…...
【Tensorflow 2.12 电影推荐项目搭建】
Tensorflow 2.12 电影推荐项目搭建 学习笔记工具、环境创建项目项目配置安装相关python包召回模型实现排序模型实现实现电影推荐导入模块设置要推荐的用户召回推荐排序推荐推荐结果结尾学习笔记 Tensorflow 2.12 电影推荐项目搭建记录~ Tensorflow是谷歌开源的机器学习框架,可…...

python+opencv特征匹配算法
pythonopencv特征匹配算法 1.安装 pip install opencv-python pip install numpy2.算法明细 import cv2 import numpy as np# 读取两张图像 img1 cv2.imread(image1.jpg,0) # queryImage img2 cv2.imread(image2.jpg,0) # trainImage# 初始化SIFT对象 sift cv2.xfeatur…...

android Compose 实现 webView
在Compose中,目前还没有原生的WebView组件。但是,您可以使用Android Jetpack组件中的AndroidView来将传统的WebView集成到Compose中。下面是一个示例代码: Composable fun WebViewScreen(url: String) {AndroidView(factory { context ->…...
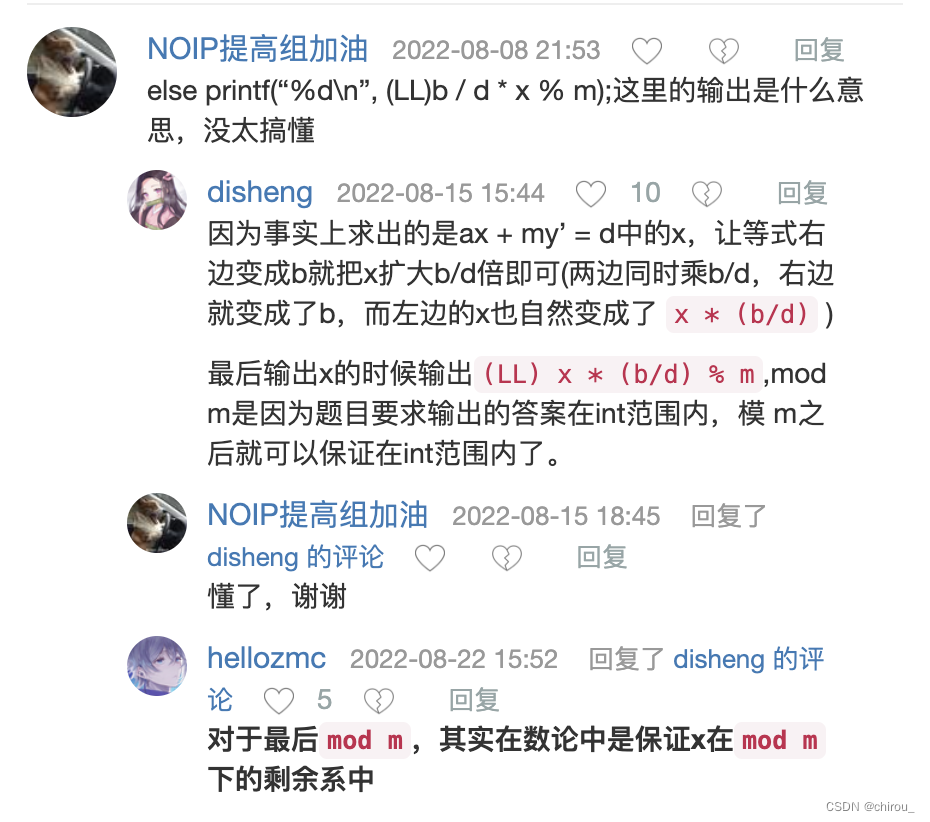
算法基础-数学知识-欧拉函数、快速幂、扩展欧几里德、中国剩余定理
算法基础-数学知识-欧拉函数、快速幂、扩展欧几里德、中国剩余定理 欧拉函数AcWing 874. 筛法求欧拉函数 快速幂AcWing 875. 快速幂AcWing 876. 快速幂求逆元 扩展欧几里德(裴蜀定理)AcWing 877. 扩展欧几里得算法AcWing 878. 线性同余方程 中国剩余定理…...
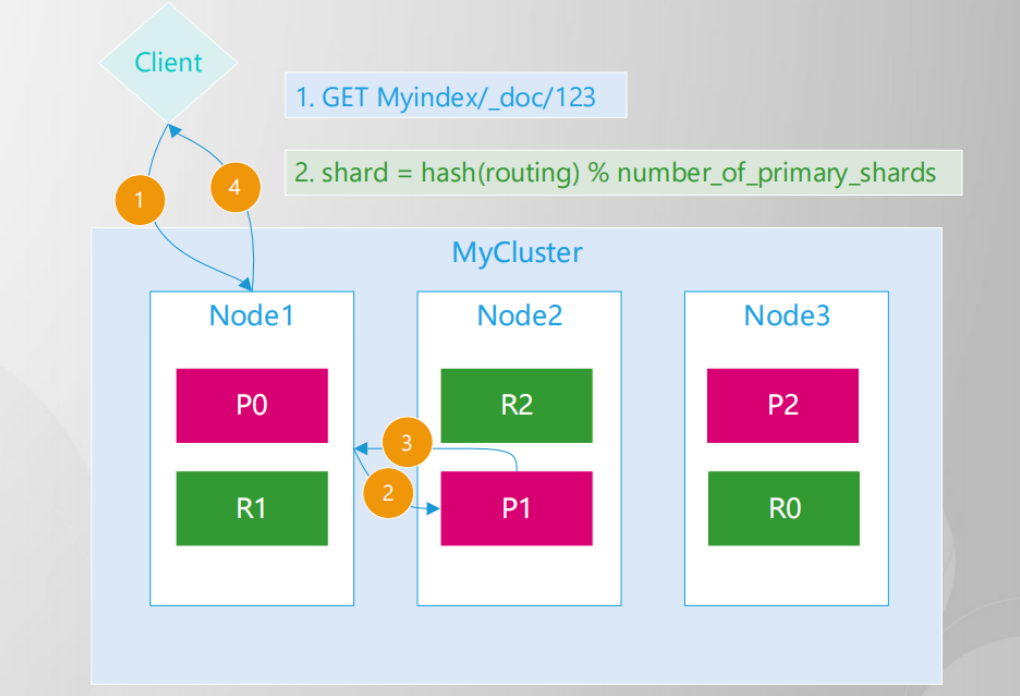
ElasticSearch系列-索引原理与数据读写流程详解
索引原理 倒排索引 倒排索引(Inverted Index)也叫反向索引,有反向索引必有正向索引。通俗地来讲,正向索引是通过key找value,反向索引则是通过value找key。ES底层在检索时底层使用的就是倒排索引。 索引模型 现有索…...

【码银送书第七期】七本考研书籍
八九月的朋友圈刮起了一股晒通知书潮,频频有大佬晒出“研究生入学通知书”,看着让人既羡慕又焦虑。果然应了那句老话——比你优秀的人,还比你努力。 心里痒痒,想考研的技术人儿~别再犹豫了。小编咨询了一大波上岸的大佬ÿ…...
和本地时区(/etc/timezone))
docker容器的设置本地时间(/etc/localtime)和本地时区(/etc/timezone)
本地时区的修改 一般情况下,我们启动docker容器时指定了环境变量: -e TZ:Asia/Ho_Chi_Minh ,容器内的时区就会变成东八区,某些软件则会读取该环境变量作为其使用的时区,该环境变量相当于"残缺版"的命令&…...

侯捷老师C++课程:内存管理
内存管理 第一讲:primitives c应用程序 c内存的基本工具 测试程序: #include <iostream> using namespace std; #include <complex> #include <ext/pool_allocator.h>int main() {// 三种使用方法void* p1 malloc(512); // 512 b…...

A股风格因子看板 (2023.09 第05期)
该因子看板跟踪A股风格因子,该因子主要解释沪深两市的市场收益、刻画市场风格趋势的系列风格因子,用以分析市场风格切换、组合风格暴露等。 今日为该因子跟踪第05期,指数组合数据截止日2023-08-31,要点如下 近1年A股风格因子检验统…...
sqoop插入hbase 脚本(增量))
修炼离线:(二)sqoop插入hbase 脚本(增量)
一:mysql创建表,插入数据。 二:hbase创建表。 habse shell create aa(表名),cf(列族)三:mysql_hbase脚本。 #!/bin/shmysqlHost$1 mysqlUserName$2 mysqlUserPass$3 mysqlDbName$4 myqlTbName$5 hbaseTbName$6 hbaseTbRowkey$7…...
跨平台编程开发工具Xojo 2023 Release mac中文版功能介绍
Xojo mac是一款跨平台的软件开发工具,它允许开发人员使用一种编程语言来创建应用程序,然后可以在多个操作系统上运行。Xojo 2023是Xojo开发工具的最新版本,它提供了许多功能和改进,以帮助开发人员更轻松地构建高质量的应用程序。 …...
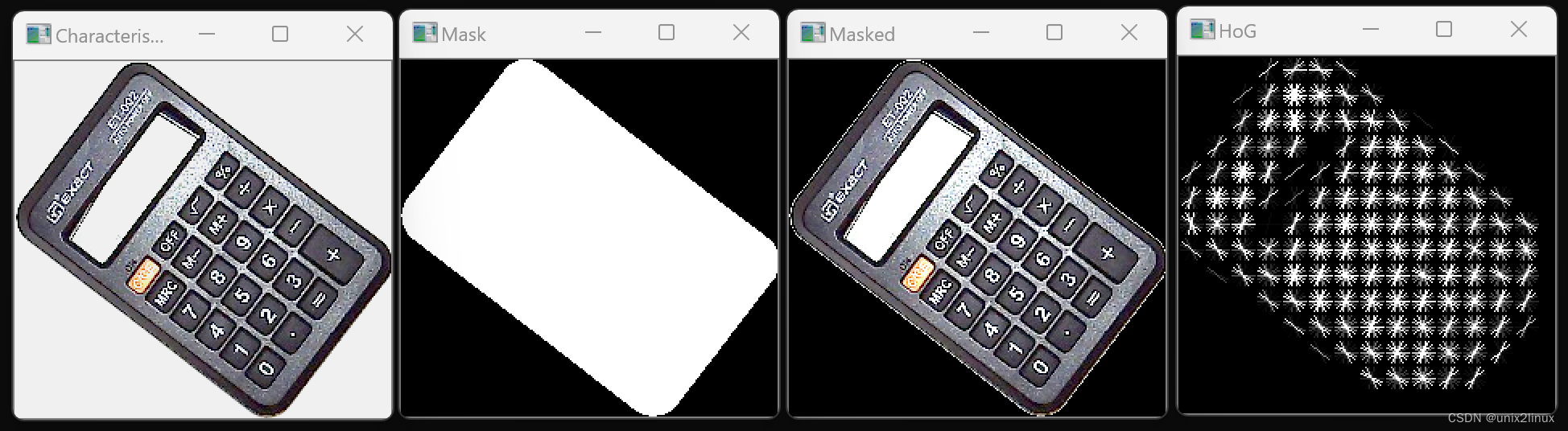
OpenCV Series : Target Box Outline Border
角点 P1 [0] (255, 000, 000) P2 [1] (000, 255, 000) P3 [2] (000, 000, 255) P4 [3] (000, 000, 000)垂直矩形框 rect cv2.minAreaRect(cnt)targetColor roi_colortargetThickness 1targetColor (255, 255, 255)if lineVerbose:if …...

【AD】【规则设置】设置四层板
设置四层板 一般 4层板,都会把 地 和 VCC放在内层。1、使用快捷键D-K 进入层叠管理器,添加负片层添加完后,修改层名,方便辨识修改格式:属性层号 2、进入相应layer 设置网络设置GND层设置VCC层特点:在层内可…...

Linux安装JDK1.8并配置环境变量
Linux安装JDK并配置环境变量Linux安装JDK并配置环境变量Linux安装JDK并配置环境变量 一、查询已有JAVA环境版本信息 java -version 二、下载Oracle JDK安装包 https://www.oracle.com/java/technologies/downloads/archive/ 三、安装 配置JDK 以下方式适用于安装各版本JDK&…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
