当前位置： 首页 > news >正文

＜Altium Designer＞ 将.DSN文件导入并转换成SchDoc文件

news 文章来源：https://blog.csdn.net/weixin_38288325/article/details/132537065 2025/1/19 11:09:59

目录

01 使用向导方式导入.DSN

02 消除Unique Identifiers Errors

03 文章总结

大家好，这里是程序员杰克。一名平平无奇的嵌入式软件工程师。

本文主要是总结和分享将OrCAD Capture画的原理图文件(.DSN)导入到Altium Designer，转换成对应的原理图文件(SchDoc)的方法。

本文所使用的编译IDE的环境：

  • Altium Designer19(AD19)
  • Cadence 17.2

下面正式进入本章推送的内容。

01 使用向导方式导入.DSN

1. 依次点击“文件(F)->导入向导”，打开导入向导界面；

图片

2. 在导入向导界面，选择“Orcad Designs and Libraries Files”，然后点击“Next”；

图片

3. 在弹出的界面点击“添加”，选择对应的.DSN文件，然后点击“Next”；

图片

图片

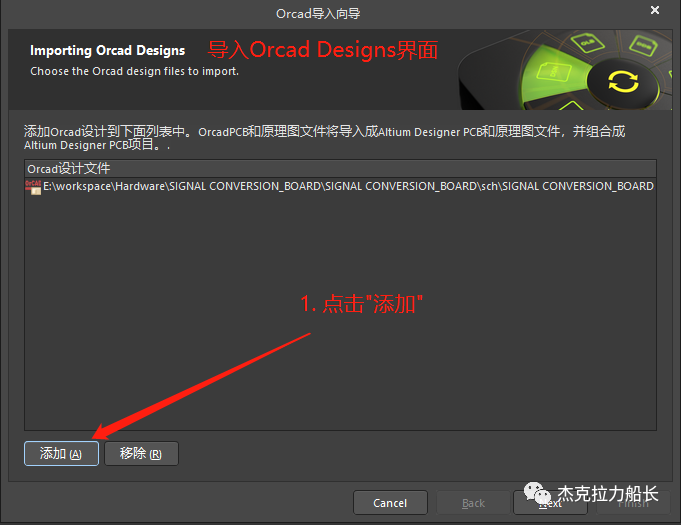
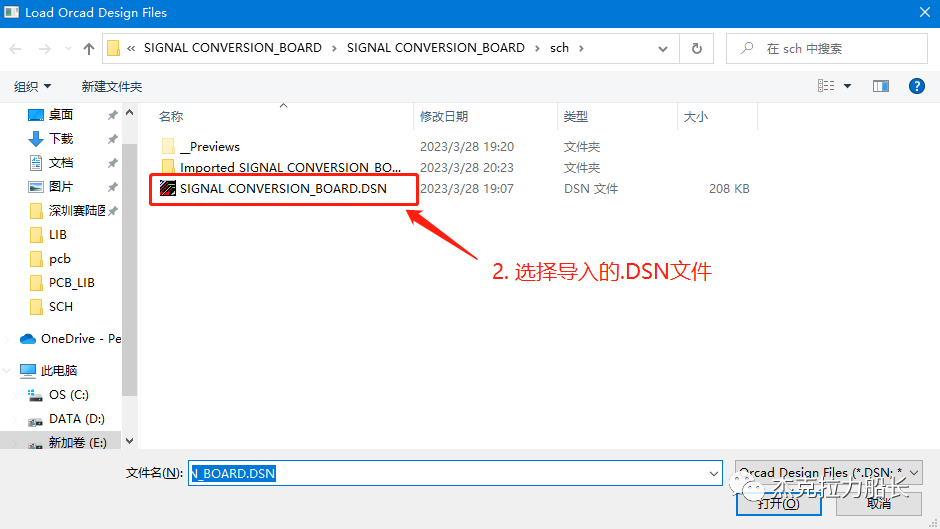
4. 弹出的“importing Orcad Libraries”界面是用于导入OrCAD的原理图库的，此处可以不导入，AD会自动根据.DSN内容进行封装的导出；

图片

5. 在“Orcad导入向导”后续的界面，一直点击“Next”，直到如下界面；此时向导操作已完成，并且生成了对应的工程以及原理图文件。

图片

02 消除Unique Identifiers Errors

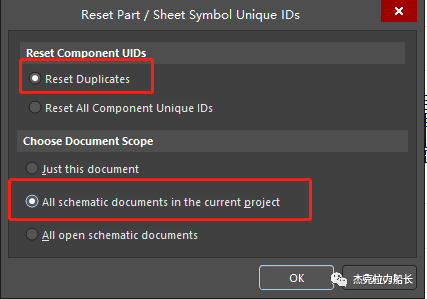
上面通过向导导入的方式，已经将.DSN文件导入AD并转换成对应.SchDoc文件，此时对工程进行编译会报错“Unique Identifiers Errors(唯一标识错误)”，这是因为向导仅仅是对元器件进行了复制，并未修改Unique ID，因此需要手动重置元器件的Unique ID。具体操作如下：

1. 打开向导生成的原理图(.SchDoc)，依次点击“工具(T)->转换(V)->重置元器件Unique ID(R)”；在弹出的界面，勾选如下设置，然后点击“OK”；此时，.DSN文件导入并转换成.SchDoc工作才算正式完成。

图片

03 文章总结

使用Altium Designer进行PCB设计还是很方面的，其与其他PCB EDA软件的转换上非常便利。本文主要是总结和分享将OrCAD Capture画的原理图文件(.DSN)导入到Altium Designer，转换成对应的原理图文件(SchDoc)的方法。

相关文章：

＜Altium Designer＞ 将.DSN文件导入并转换成SchDoc文件

目录 01 使用向导方式导入.DSN 02 消除Unique Identifiers Errors 03 文章总结 大家好，这里是程序员杰克。一名平平无奇的嵌入式软件工程师。 本文主要是总结和分享将OrCAD Capture画的原理图文件(.DSN)导入到Altium Designer，转换成对应的原理图文件…...

编程日记 2023/9/21 15:31:26

视频定格合璧，批量剪辑轻松插入图片

大家好！想要将视频与图片完美融合吗？现在，我们为您推出一款强大的批量剪辑工具，让您能够轻松在图片中插入视频，让您的创作更加精彩动人！ 首先，第一步我们要进入媒体梦工厂主页面，并…...

编程日记 2023/9/21 15:30:24

【Tensorflow 2.12 电影推荐项目搭建】

Tensorflow 2.12 电影推荐项目搭建 学习笔记工具、环境创建项目项目配置安装相关python包召回模型实现排序模型实现实现电影推荐导入模块设置要推荐的用户召回推荐排序推荐推荐结果结尾学习笔记 Tensorflow 2.12 电影推荐项目搭建记录~ Tensorflow是谷歌开源的机器学习框架，可…...

编程日记 2023/9/21 15:28:21

python+opencv特征匹配算法

pythonopencv特征匹配算法 1.安装 pip install opencv-python pip install numpy2.算法明细 import cv2 import numpy as np# 读取两张图像 img1 cv2.imread(image1.jpg,0) # queryImage img2 cv2.imread(image2.jpg,0) # trainImage# 初始化SIFT对象 sift cv2.xfeatur…...

编程日记 2023/9/21 15:27:19

android Compose 实现 webView

在Compose中，目前还没有原生的WebView组件。但是，您可以使用Android Jetpack组件中的AndroidView来将传统的WebView集成到Compose中。下面是一个示例代码： Composable fun WebViewScreen(url: String) {AndroidView(factory { context ->…...

编程日记 2023/9/21 15:25:16

算法基础-数学知识-欧拉函数、快速幂、扩展欧几里德、中国剩余定理

算法基础-数学知识-欧拉函数、快速幂、扩展欧几里德、中国剩余定理 欧拉函数AcWing 874. 筛法求欧拉函数 快速幂AcWing 875. 快速幂AcWing 876. 快速幂求逆元 扩展欧几里德（裴蜀定理）AcWing 877. 扩展欧几里得算法AcWing 878. 线性同余方程 中国剩余定理…...

编程日记 2023/9/21 15:24:15

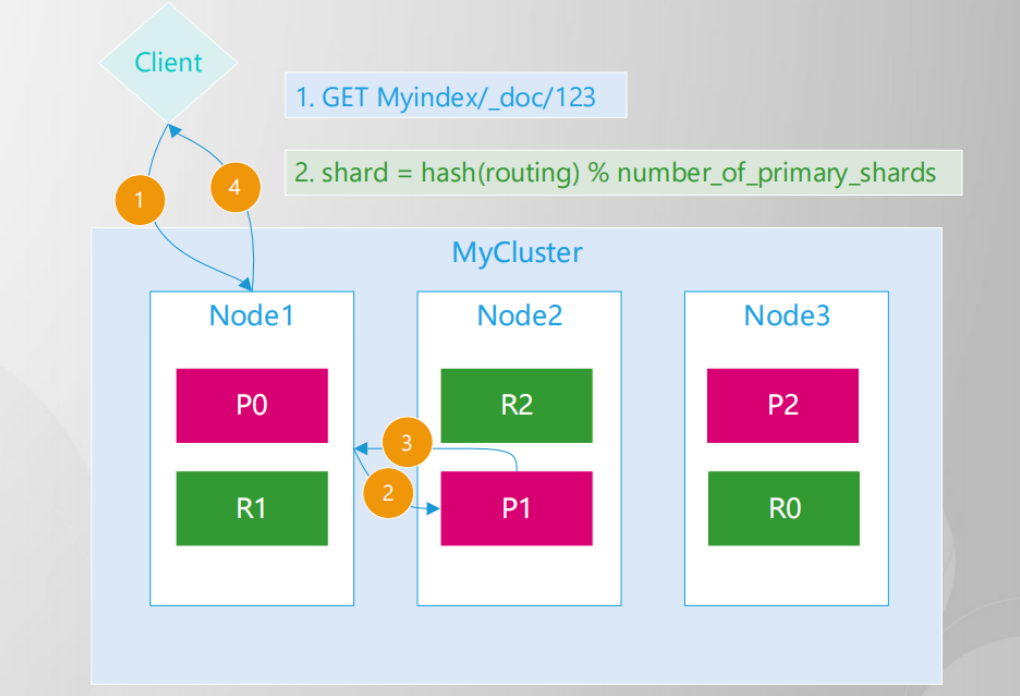
ElasticSearch系列-索引原理与数据读写流程详解

索引原理 倒排索引 倒排索引（Inverted Index）也叫反向索引，有反向索引必有正向索引。通俗地来讲，正向索引是通过key找value，反向索引则是通过value找key。ES底层在检索时底层使用的就是倒排索引。 索引模型 现有索…...

编程日记 2023/9/21 15:23:08

【码银送书第七期】七本考研书籍

八九月的朋友圈刮起了一股晒通知书潮，频频有大佬晒出“研究生入学通知书”，看着让人既羡慕又焦虑。果然应了那句老话——比你优秀的人，还比你努力。 心里痒痒，想考研的技术人儿~别再犹豫了。小编咨询了一大波上岸的大佬&#xff…...

编程日记 2023/9/21 15:21:05

docker容器的设置本地时间（/etc/localtime）和本地时区（/etc/timezone）

本地时区的修改 一般情况下，我们启动docker容器时指定了环境变量： -e TZ:Asia/Ho_Chi_Minh ，容器内的时区就会变成东八区，某些软件则会读取该环境变量作为其使用的时区，该环境变量相当于"残缺版"的命令&…...

编程日记 2023/9/21 15:20:04

侯捷老师C++课程：内存管理

内存管理 第一讲&#xff1a;primitives c应用程序 c内存的基本工具 测试程序&#xff1a; #include <iostream> using namespace std; #include <complex> #include <ext/pool_allocator.h>int main() {// 三种使用方法void* p1 malloc(512); // 512 b…...

编程日记 2023/9/21 15:18:00

A股风格因子看板 (2023.09 第05期)

该因子看板跟踪A股风格因子&#xff0c;该因子主要解释沪深两市的市场收益、刻画市场风格趋势的系列风格因子&#xff0c;用以分析市场风格切换、组合风格暴露等。 今日为该因子跟踪第05期&#xff0c;指数组合数据截止日2023-08-31&#xff0c;要点如下 近1年A股风格因子检验统…...

编程日记 2023/9/21 15:16:58

修炼离线：（二）sqoop插入hbase 脚本（增量）

一&#xff1a;mysql创建表&#xff0c;插入数据。 二&#xff1a;hbase创建表。 habse shell create aa(表名),cf(列族)三&#xff1a;mysql_hbase脚本。 #!/bin/shmysqlHost$1 mysqlUserName$2 mysqlUserPass$3 mysqlDbName$4 myqlTbName$5 hbaseTbName$6 hbaseTbRowkey$7…...

编程日记 2023/9/21 15:15:54

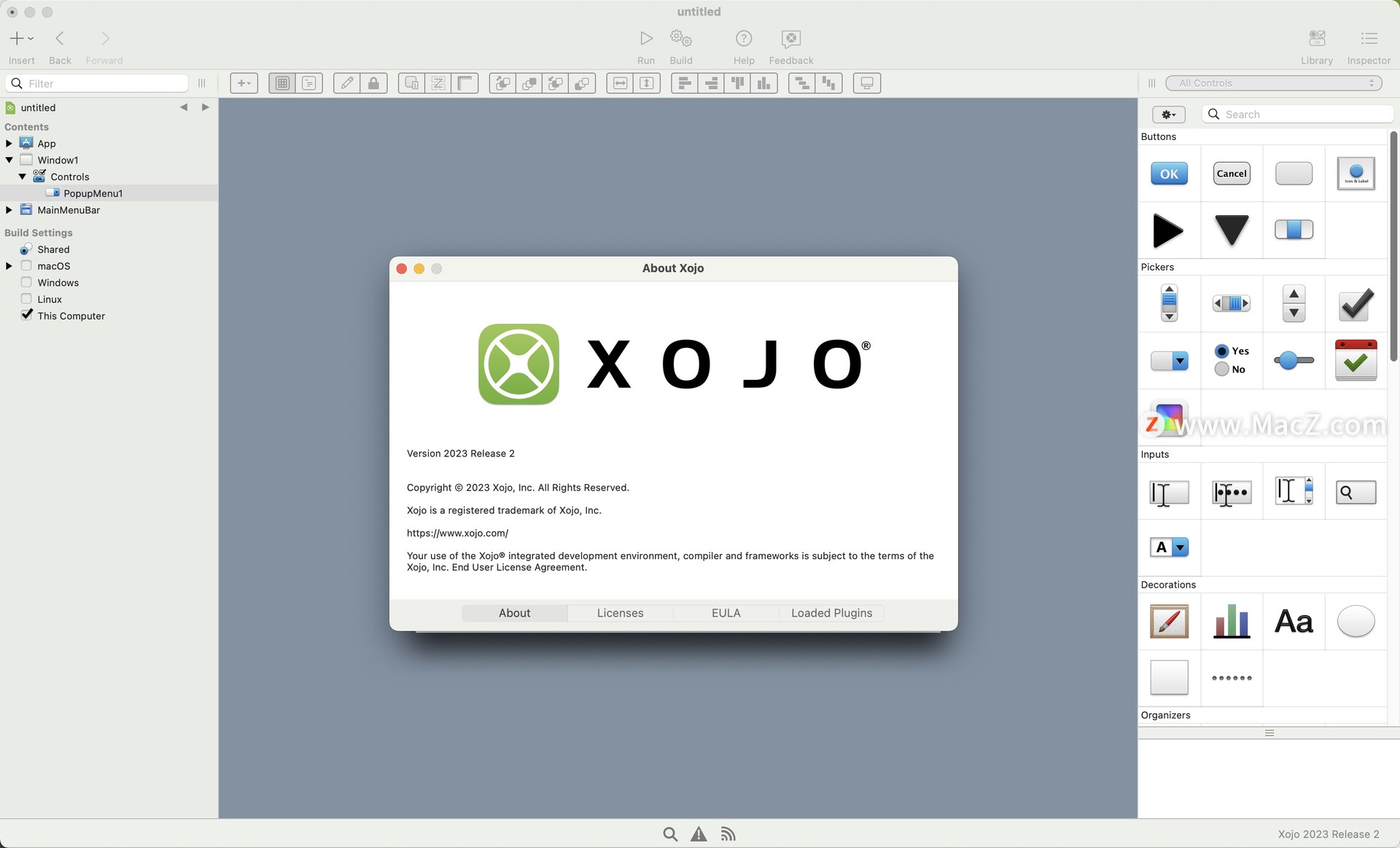
跨平台编程开发工具Xojo 2023 Release mac中文版功能介绍

Xojo mac是一款跨平台的软件开发工具&#xff0c;它允许开发人员使用一种编程语言来创建应用程序&#xff0c;然后可以在多个操作系统上运行。Xojo 2023是Xojo开发工具的最新版本&#xff0c;它提供了许多功能和改进&#xff0c;以帮助开发人员更轻松地构建高质量的应用程序。 …...

编程日记 2023/9/21 15:14:52

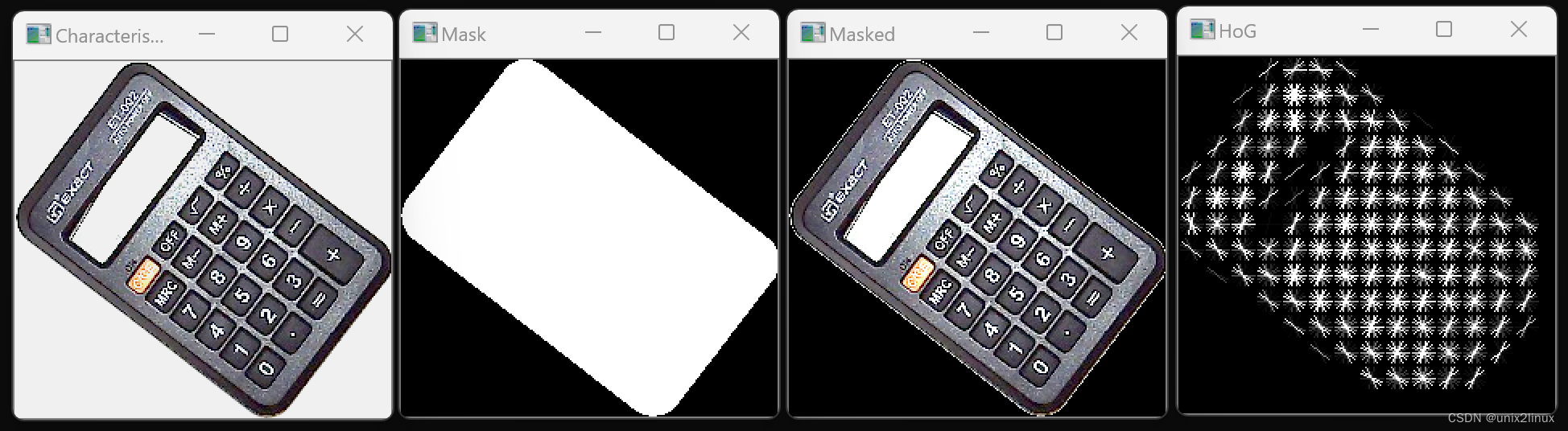
OpenCV Series : Target Box Outline Border

角点 P1 [0] (255, 000, 000) P2 [1] (000, 255, 000) P3 [2] (000, 000, 255) P4 [3] (000, 000, 000)垂直矩形框 rect cv2.minAreaRect(cnt)targetColor roi_colortargetThickness 1targetColor (255, 255, 255)if lineVerbose:if …...

编程日记 2023/9/21 15:13:51

【AD】【规则设置】设置四层板

设置四层板 一般 4层板&#xff0c;都会把 地 和 VCC放在内层。1、使用快捷键D-K 进入层叠管理器&#xff0c;添加负片层添加完后&#xff0c;修改层名&#xff0c;方便辨识修改格式&#xff1a;属性层号 2、进入相应layer 设置网络设置GND层设置VCC层特点&#xff1a;在层内可…...

编程日记 2023/9/21 15:12:50

Linux安装JDK1.8并配置环境变量

Linux安装JDK并配置环境变量Linux安装JDK并配置环境变量Linux安装JDK并配置环境变量 一、查询已有JAVA环境版本信息 java -version 二、下载Oracle JDK安装包 https://www.oracle.com/java/technologies/downloads/archive/ 三、安装 配置JDK 以下方式适用于安装各版本JDK&…...

编程日记 2023/9/21 15:11:49

面向面试知识--MySQL数据库与索引

面向面试知识–MySQL数据库与索引 优化难点与面试点 什么是MySQL索引&#xff1f; 索引的MySQL官方定义&#xff1a;索引是帮助MySQL快速获取数据的数据结构。 动力节点原文&#xff1a; MysQL官方对于索引的定义:索引是帮助MySQL高效获取数据的数据结构。 MysQL在存储数据之…...

编程日记 2023/9/21 15:09:43

portainer + portainer/agent

参考链接 https://docs.portainer.io/ portainer 免费版 portainer-ce 免费版 portainer-ee 企业版 portainer-agent docker本机代理 agent 下载地址 https://download.csdn.net/download/a309450028a/87451332 portainer 下载地址 https://download.csdn…...

编程日记 2023/9/21 15:08:41

C# 截取字符串

在 C# 中&#xff0c;可以使用 Substring 方法来截取字符串的一部分。该方法有两个参数&#xff1a;起始索引和要截取的字符数。 以下是使用 Substring 方法截取字符串的示例&#xff1a; string str "Hello World"; string result str.Substring(6); // 从索引为…...

编程日记 2023/9/21 15:07:40

FOXBORO FBM233 P0926GX控制脉冲模块

FOXBORO FBM233 P0926GX 是一种控制脉冲模块&#xff0c;通常用于工业自动化和控制系统中。这个模块的主要功能是生成和控制脉冲信号&#xff0c;以用于执行特定的操作或控制过程。以下是可能适用于 FOXBORO FBM233 P0926GX 控制脉冲模块的一些常见特点&#xff1a; 脉冲生成&a…...

编程日记 2023/9/21 15:05:37

MySQL性能优化——MYSQL执行流程

MySQL 执行流程1-5如下图。 MySQL 的架构共分为两层&#xff1a;Server 层和存储引擎层&#xff0c; Server 层负责建立连接、分析和执行 SQL。MySQL 大多数的核心功能模块都在这实现&#xff0c;主要包括连接器&#xff0c;查询缓存、解析器、预处理器、优化器、执行器等。…...

编程日记 2023/9/21 15:04:34

Django：四、Djiango如何连接使用MySQL数据库

一、安装数据库第三方插件 安装下载mysql第三方插件 pip install mysqlclient 二、创建MySQL数据库 ORM可以帮助我们做两件事&#xff1a; 创建、修改、删除数据库中的表&#xff08;不用写SQL语句&#xff09;&#xff0c;但无法创建数据库操作表中的数据&#xff08;不用…...

编程日记 2023/9/21 15:02:30

LeetCode 热题 100（八）：贪心。121. 买卖股票的最佳时机、45. 跳跃游戏 II

题目一&#xff1a; 121. 买卖股票的最佳时机https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/ 思路&#xff1a;因为时间复杂度O&#xff08;n&#xff09;&#xff0c;所以使用贪心来做。类似双指针&#xff0c;一个指针记录到当前循环时最小的股票价格&…...

编程日记 2023/9/21 15:01:29

第N个数字

给你一个整数 n &#xff0c;请你在无限的整数序列 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …] 中找出并返回第 n 位上的数字。 我觉得这题是哪以理解的 看这个题解 func findNthDigit(n int) int {digit : 1start : 1count : 9for n > count {n - countdigitstart start …...

编程日记 2023/9/21 15:00:27

【适用于电力系统和音频系统】计算信号的总谐波失真 （THD）（Matlab代码实现）

&#x1f4a5;&#x1f4a5;&#x1f49e;&#x1f49e;欢迎来到本博客❤️❤️&#x1f4a5;&#x1f4a5; &#x1f3c6;博主优势&#xff1a;&#x1f31e;&#x1f31e;&#x1f31e;博客内容尽量做到思维缜密&#xff0c;逻辑清晰&#xff0c;为了方便读者。 ⛳️座右铭&a…...

编程日记 2023/9/21 14:59:25

kubernetes（k8s）PVC

概念 PVC 的全称是&#xff1a;PersistentVolumeClaim&#xff08;持久化卷声明&#xff09;&#xff0c;PVC 是用户存储的一种声明&#xff0c;PVC 和 Pod 比较类似&#xff0c;Pod 消耗的是节点&#xff0c;PVC 消耗的是 PV 资源&#xff0c;Pod 可以请求 CPU 和内存&#x…...

编程日记 2023/9/21 14:57:22

Android ANR问题触发机制

1 Anr类型 ​ Anr一般有四种类型。 1.1 input dispatching timeout ​ 主要时按键或触摸屏事件在5s内没有响应。这个时间在ActivityManagerService中定义。 C:\Users\wangjie\AppData\Local\Android\Sdk\sources\android-32\com\android\server\am\ActivityManagerService.…...

编程日记 2023/9/21 14:56:20

解决jupyter找不到虚拟环境的问题

解决jupyter找不到虚拟环境的问题 使用jupyter只能使用base环境&#xff0c;不能找到自己创建的虚拟环境。如下图&#xff0c;显示的默认的虚拟环境base的地址。 如何解决这个问题&#xff1f;需要两个步骤即可 1 . 在base环境中安装nb_conda_kernels这个库 activate base c…...

编程日记 2023/9/21 14:55:18

Unity丨移动相机朝向目标并确定目标在摄像机可视范围内丨摄像机注释模型丨摄像机移动丨不同尺寸模型优化丨

文章目录 问题描述功能展示技术细节小结 问题描述 本文提供的功能是摄像机朝向目标移动&#xff0c;并确定整个目标出现在摄像机视角内&#xff0c;针对不同尺寸的模型优化。 功能展示 提示&#xff1a;这里可以添加技术名词解释 技术细节 直接上代码 using UnityEngine;…...

编程日记 2023/9/21 14:54:16

排序算法：归并排序（递归和非递归）

朋友们、伙计们&#xff0c;我们又见面了&#xff0c;本期来给大家解读一下有关排序算法的相关知识点&#xff0c;如果看完之后对你有一定的启发&#xff0c;那么请留下你的三连&#xff0c;祝大家心想事成&#xff01; C 语 言 专 栏&#xff1a;C语言&#xff1a;从入门到精通…...

编程日记 2023/9/21 14:53:14

泰兴做网站的公司/市场营销毕业论文

题目描述 给定一个字符串 s &#xff0c;请你找出其中不含有重复字符的 最长连续子字符串 的长度。 示例 示例 1: 输入: s “abcabcbb” 输出: 3 解释: 因为无重复字符的最长子字符串是 “abc”&#xff0c;所以其长度为 3。 示例 2: 输入: s “bbbbb” 输出: 1 解释: 因…...

编程日记 2025/1/19 7:56:05

wordpress siren主题/引流软件

我希望通过博客的形式记录自己项目和基础积累的过程&#xff0c;这篇是算法以及程序设计的开篇。 题目&#xff1a;poj1753 Flip Game Time:1000MS Mem:65536K 描述&#xff1a;黑白两面的棋子&#xff0c;给一个4*4棋盘&#xff0c;每轮可以翻动其中任意一个棋子&#xff0…...

编程日记 2025/1/19 5:27:23

网站 内容建设存在的问题/链接推广

usingSystem; usingSystem.IO; usingSystem.Web; namespaceSEC { /**//**//**//// /// 对文件和文件夹的操作类 /// public class FileControl { public FileControl() { } /**//**//**//// /// 在根目录下创建文件夹 /// /// 要创建的文件路径 public void CreateFolder(strin…...

编程日记 2025/1/19 4:41:01

深圳定制巴士怎么买票/嘉兴seo网络推广

Mock测试就是在测试过程中&#xff0c;对于某些不容易构造或者不容易获取的对象&#xff0c;用一个虚拟的对象来创建以便测试的测试方法。什么是不容易构造的对象呢&#xff1f;例如HttpServletRequest&#xff0c;需要在有servlet容器环境中创建获取。那不容易获取的对象呢&am…...

编程日记 2025/1/19 1:37:56

做网站的害处/百度统计代码安装位置

【斗蟹攻略】Navicat 为 MySQL、Oracle、PostgreSQL、SQL Server 和 MariaDB 提供安全性管理工具。用户可以新建、编辑、删除用户、授予或撤消已选择的数据库及它们数据库对象的权限。点击“用户”图标可打开用户对象列表&#xff0c;用户对象列表将显示服务器中的所有用户。下…...

编程日记 2025/1/18 23:01:05

怎么下载在别的网站上用的js特效/网站推广方案有哪些

文章目录C 输入std::operator>>std::getlinestd::istream::getlinestd::istream::getstd::istream::ignore总结牛客 OJ 输入输出练习AB(1)AB(2)AB(3)AB(4)AB(5)AB(6)AB(7)字符串排序(1)字符串排序(2)字符串排序(3)自测本地通过提交为0C 输入 std::operator>> #in…...

编程日记 2025/1/18 21:14:22