一、八大排序(sort)
文章目录
- 一、时间复杂度
- (一)定义:常数操作
- 二、空间复杂度
- (一)定义:
- 三、排序
- (一)选择排序
- 1.定义
- 2.代码
- 3.特性
- (二)冒泡排序
- 1.定义
- 2.代码
- 3.特性
- (三)插入排序
- 1.定义
- 2.代码
- 3.特性
- (四)归并排序
- 1.定义
- 2.代码
- 3.特性
- (五)快速排序
- (六)堆排序
- (七)基数排序
- (八)计数排序
一、时间复杂度
(一)定义:常数操作
与数据量无关,是一个固定的东西。
一个操作如果和样本数量没有关系,每次都是固定时间内完成的操作,就叫做常数操作。
时间复杂度为一个算法流程中,常数操作数量的一个指标。常用o(读作big o)来表示。具体来说,先要对一个算法流程非常熟悉,然后去写出这个算法流程中,发生了多少常数操作,进而总结出常数操作数量的表达式。
评价一个算法流程的好坏,先看时间复杂度的指标,然后再分析不同数据样本下的实际运行时间,也就是“常数项时间”。
二、空间复杂度
(一)定义:
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的一个量度,同样反映的是一个趋势。
三、排序
(一)选择排序
1.定义
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完。

2.代码
void process(vector<int> &arr) {if (arr == nullptr || arr.size() < 2) {return ;}for (int i = 0 ; i < arr.size() - 1; i++) { // 当前位置int minIndex = i;for (int j = i + 1; j < arr.size(); j++) {minIndex = arr[j] < arr[minIndex] ? j : minIndex;}swap(arr,i,minIndex);}
}
void swap(vector<int> &arr,int j,int j) {arr[i] = arr[i] ^ arr[j];arr[j] = arr[i] ^ arr[j];arr[i] = arr[i] ^ arr[j];
}
3.特性
-
容易理解,但是效率太低,实际当中不太使用
-
时间复杂度O(n^2),空间复杂度O(1);

-
不稳定
(二)冒泡排序
1.定义
在要排序的一组数中,对当前还未排好序的范围内的全部数,自上而下对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。即:每当两相邻的数比较后发现它们的排序与排序要求相反时,就将它们互换。
2.代码
void bubbleSort(vector<int> &arr) {if (arr == nullptr || arr.size() < 2) {return ;}int n = arr.size();for (int i = 0; i < n; i++) { // //控制交换次数for (int j = 0; j < n - i - 1; j ++) { // //向后冒泡 ,控制边界if(arr[j] > arr[j+1])//如果前一个值大于后一个值,交换{swap(arr[j],arr[j+1]);} }}
}
3.特性
- 容易理解
- 时间复杂度O(n^2),空间复杂度O(1)
- 稳定
(三)插入排序
1.定义
插入排序的步骤如下:每次从无序部分中取出一个元素,与有序部分中的元素从后向前依次进行比较,并找到合适的位置,将该元素插到有序组当中。
例:对于数组 [3,2,5,4,2,3,3] 进行插入排序的详细过程:
1、0~0位置上做到有序 ——>就一个数 做到了
2、0~1位置上做到有序 ——>2比3小 2 3互换位置——> [2,3,5,4,2,3,3]
3、0~2位置上做到有序 ——>5比3大 位置不动——> [2,3,5,4,2,3,3]
4、0~3位置上做到有序 ——>4比5小 4 5互换位置——> [2,3,4,5,2,3,3]——>4比3大 位置不动
5、0~4位置上做到有序 ——>2比5小 2 5互换位置——> [2,3,4,2,5,3,3]
——>2比4小 2 4互换位置——> [2,3,2,4,5,3,3]——>2比3小 2 3互换位置——> [2,2,3,4,5,3,3]
2比2相等 位置不动
6、0~5位置上做到有序 ——>3比5小 3 5互换位置——> [2,2,3,4,3,5,3]
——>3比4小 3 4互换位置——> [2,2,3,3,4,5,3]——>3比3相等 位置不动
7、0~6位置上做到有序 ——>3比5小 3 5互换位置——> [2,2,3,3,4,3,5]
——>3比4小 3 4互换位置——> [2,2,3,3,3,4,5]——>3比3相等 位置不动
2.代码
void insertSort(vector<int> &arr) {if (arr == nullptr || arr.size() < 2) {return ;}for (int i = 1; i < arr.size(); i++) { // 0 - 0 有序的for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1] ; j--) { // 想有序swap(arr,j, j + 1);}}
}3.特性
- 元素集合越接近有序,直接插入排序算法的时间效率越高
- 时间复杂度:O(n^2)(情况最差时,即逆序转有序,最好为O(n));
- 空间复杂度:O(1);
- 稳定
(四)归并排序
1.定义
对于一个数组从中点的位置分开,先让左侧部分排好序,再让右边部分排好序,然后整体整合。
将图中左侧部分和右侧部分分别排好序,然后使用两个指针分别从两部分的最左侧开始,在内存中单独开辟一个空间 ,这时我们比较两个指针指向的数的大小,左侧小于等于右侧的时候,将左侧部分指针指向的值拷贝到辅助空间中,然后左侧指针右移一位。如果右侧部分指针指向的值小于左侧的,则将右侧部分指针指向的值拷贝到辅助空间中,然后右侧指针右移一位。依次循环,如果哪侧越界了,将剩下的部分直接拷贝到辅助空间中。将辅助空间拷贝到原数组。
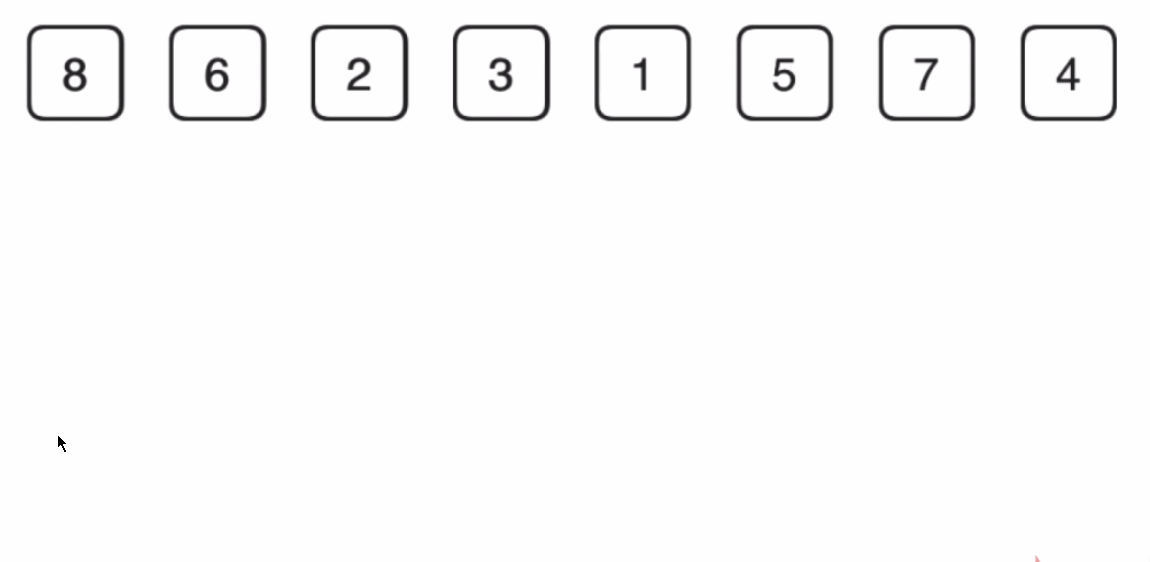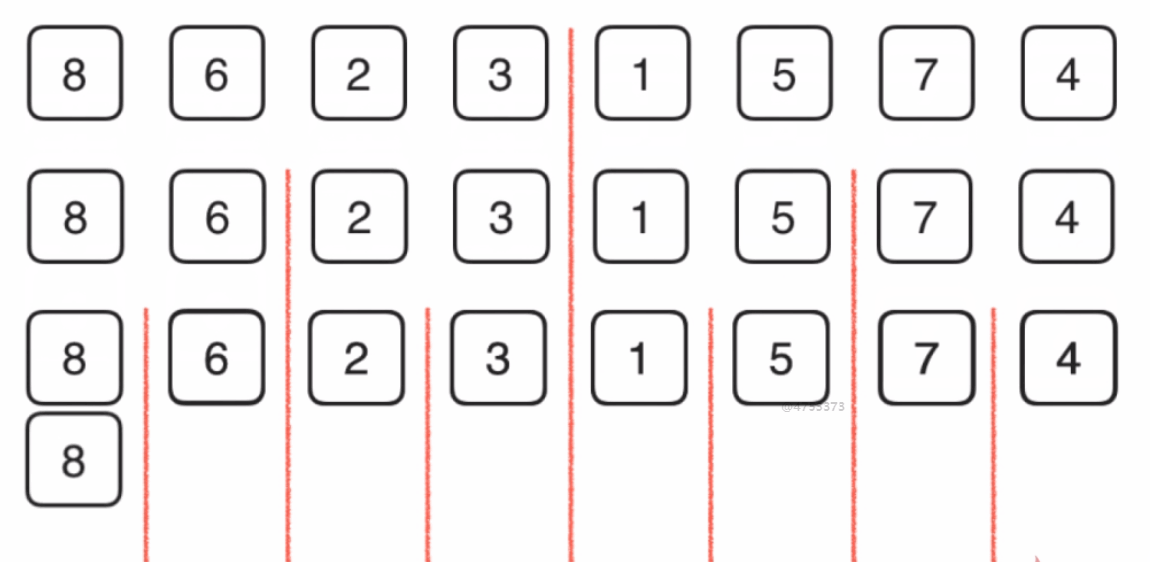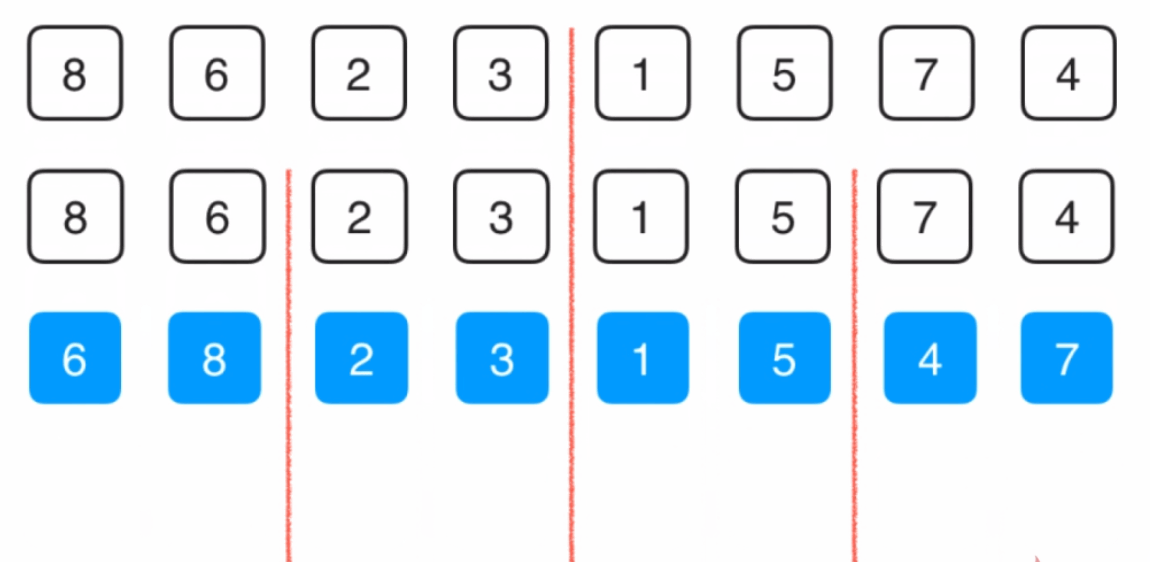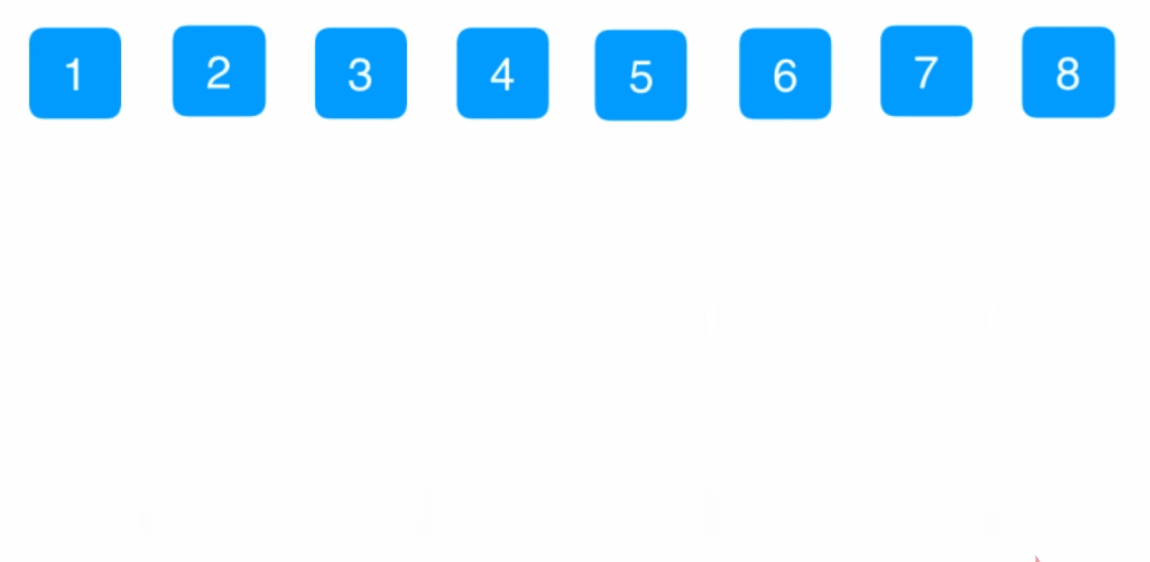
2.代码
3.特性
- 整体就是简单的递归,左边排好序、右边排好序、让整体有序
- 让其整体有序的过程里用了排外序的方法
- 利用master公式来求解时间复杂度
- 归并排序的实质
(五)快速排序
(六)堆排序
(七)基数排序
(八)计数排序
相关文章:

一、八大排序(sort)
文章目录 一、时间复杂度(一)定义:常数操作 二、空间复杂度(一)定义: 三、排序(一)选择排序1.定义2.代码3.特性 (二)冒泡排序1.定义2.代码3.特性 (…...
【AWS】AI 代码生成器—Amazon CodeWhisperer初体验 | 开启开挂编程之旅
使用 AI 编码配套应用程序更快、更安全地构建应用程序 文章目录 1.1 Amazon CodeWhisperper简介1.2 Amazon CodeWhisperer 定价2.1 打开VS Code2.2 安装AWS ToolKit插件 一、前言 1.1 Amazon CodeWhisperper简介 1️⃣更快地完成更多工作 CodeWhisperer 经过数十亿行代码的训…...

【Mysql主从配置方法---单主从】
Mysql主从 主服务器 创建用户 create user “for_rep”“从服务器IP地址” IDENTIFIED by “123456” 授权 grant replication slave on . to “for_rep”“从服务器IP地址” IDENTIFIED by “123456” 查看用户权限 SHOW GRANTS FOR “for_rep”“从服务器IP地址”; 修改M…...

⼀⽂读懂加密资产交易赛道的新锐⼒量Bitdu
交易所,仍然是加密资产赛道的皇冠级赛道。围绕这个领域展开的商业竞争,最能引起⼴⼤⽤⼾的关注。 经历了数轮资产价格涨跌的⽜熊之后,⼀批批创业者也在不断地思考这⼀议题 — 如何在去中⼼化的世界中,最⾼效率地集结流量、资本和…...
万里牛与金蝶云星空对接集成查询调拨单连通调拨单新增(万里牛调拨单-金蝶【直接调拨单】)
万里牛与金蝶云星空对接集成查询调拨单连通调拨单新增(万里牛调拨单-金蝶【直接调拨单】) 源系统:万里牛 万里牛是杭州湖畔网络技术有限公司旗下SaaS软件品牌,主要针对电商、外贸、实体门店等业务群体,帮助企业快速布局新零售,提升订单处理效…...
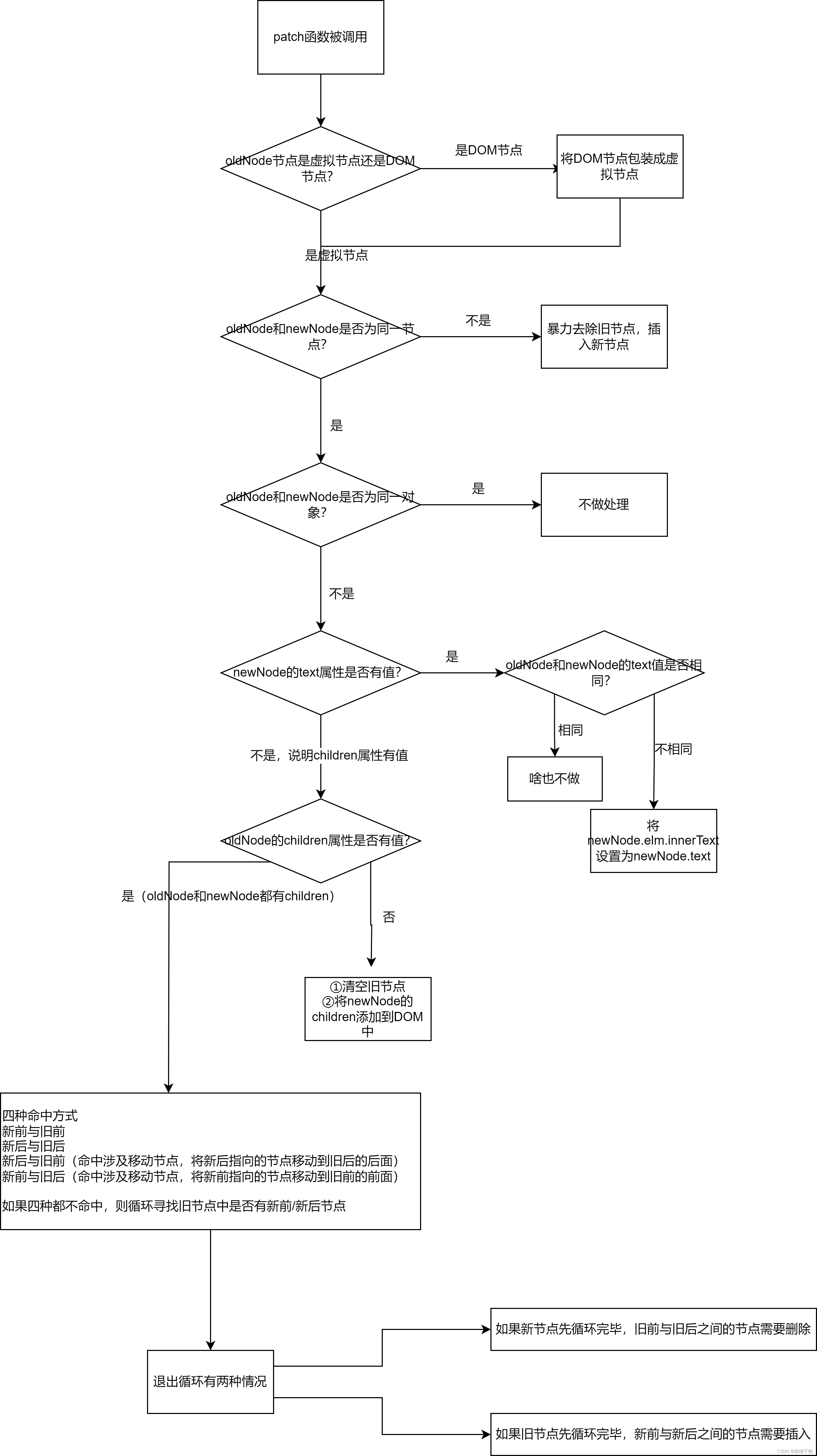
虚拟DOM与diff算法
虚拟DOM与diff算法 snabbdom虚拟DOMdiff算法 snabbdom 是什么:snabbdom是著名的虚拟DOM库,是diff算法的鼻祖,Vue源码借鉴了snabbdom 虚拟DOM 是什么:本质上是存在内存里的 JavaScript 对象 作用:用来描述真实DOM的层…...

K8S:pod资源限制及探针
文章目录 一.pod资源限制1.pod资源限制方式2.pod资源限制指定时指定的参数(1)request 资源(2) limit 资源(3)两种资源匹配方式 3.资源限制的示例(1)官网示例(2࿰…...

CSS中的定位
position 的属性与含义 CSS 中的 position 属性用于控制元素在页面中的定位方式,有四个主要的取值,每个取值都会影响元素的布局方式,它们是: static(默认值): 这是所有元素的初始定位方式。在静…...
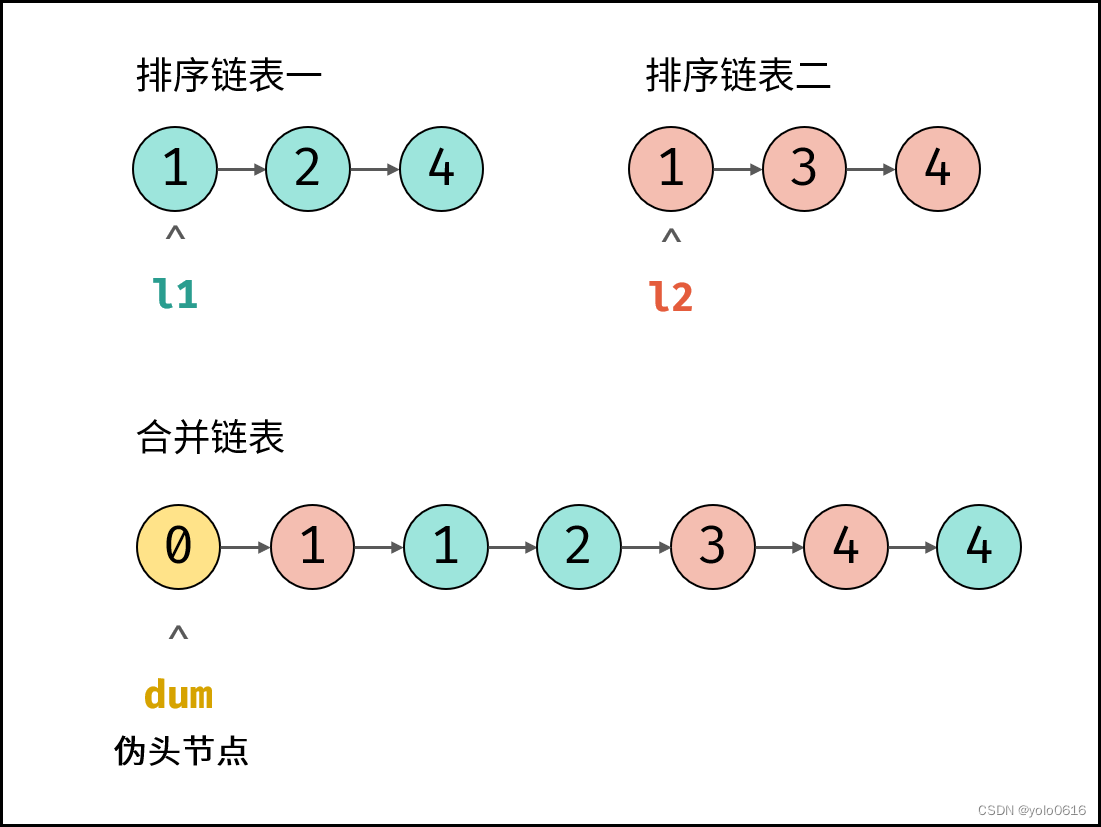
二、链表(linked-list)
文章目录 一、定义二、经典例题(一)[21.合并两个有序链表](https://leetcode.cn/problems/merge-two-sorted-lists/description/)1.思路2.复杂度分析3.注意4.代码 (二)[86.分割链表](https://leetcode.cn/problems/partition-list…...
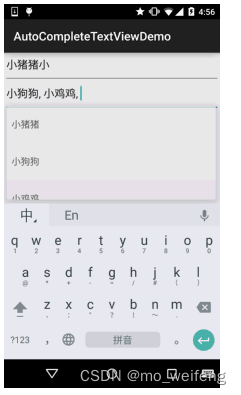
Android EditText筛选+选择功能开发
在日常开发中经常会遇到这种需求,EditText既需要可以筛选,又可以点击选择。这里筛选功能用的是AutoCompleteTextView,选择功能使用的是第三方库https://github.com/kongzue/DialogX。 Android AutoCompleteTextView(自动完成文本框)的基本使用…...

Linux 信号 alarm函数 setitimer函数
/*#include <unistd.h>unsigned int alarm(unsigned int seconds);功能:设置定时器。函数调用,开始倒计时,0的时候给当前的进程发送SIGALARM信号参数:倒计时的时长。。单位:秒 如果参数为0,无效返回…...

自主设计,模拟实现 RabbitMQ - 实现发送方消息确认机制
目录 一、实现发送方消息确认 1.1、需求分析 什么是发送方的消息确认? 如何实现?...

【数据结构】二叉树的·深度优先遍历(前中后序遍历)and·广度优先(层序遍历)
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...
优彩云采集器下载-免费优彩云采集器下载地址
免费优彩云采集器。您是否曾为了数据采集而感到头疼不已?是否一直在寻找一种能够轻松、高效地获取所需数据的方法?别着急,让我们一起来了解如何通过优彩云采集器解决这些问题,从而让您产生购买的欲望。 免费全自动采集发布批量管理…...

【Python】OJ 常用函数
这里写目录标题 一. math1. 求阶乘 - factorial()2. 绝对值 - fabs() 二. 容器的方法1. reverse() 三. Python 内置函数1. sort() 一. math 需要引入 math 包:import math 1. 求阶乘 - factorial() import math print(math.factorial(5))--------运行结果-------…...

【Vue】上万个字把事件处理讲解的淋漓尽致
hello,我是小索奇,精心制作的Vue系列教程持续更新哈,想要学习&巩固&避坑就一起学习吧~ 事件处理 事件的基本用法 重点内容 使用v-on:xxx缩写xxx绑定事件,其中 xxx 是事件名(回顾:v-bind缩写为冒号…...

Remmina中VNC、SSH和RDP的区别
Remmina 可以在 Linux 系统上对远程进行连接。它支持多种远程连接协议,包括 VNC(Virtual Network Computing)、SSH(Secure Shell)和 RDP(Remote Desktop Protocol)。这些协议用于实现不同类型的…...
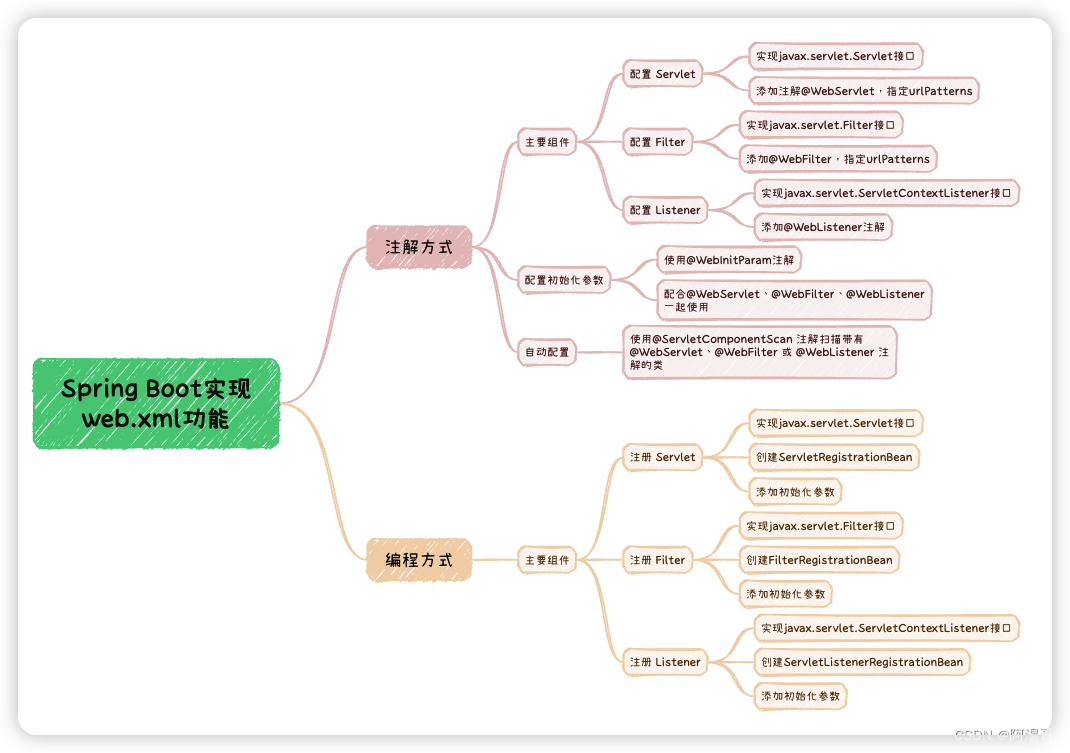
Spring Boot实现web.xml功能
Spring Boot实现web.xml功能 1. 基于注解实现1.1 组件注册1.2 WebInitParam注解 2. 基于编码实现2.1 Servlet & Filter2.2 Listener 3. 总结 在Spring Boot中,不再需要使用传统的 web.xml 文件来配置web应用的功能,Spring Boot支持通过注解和基于代码…...
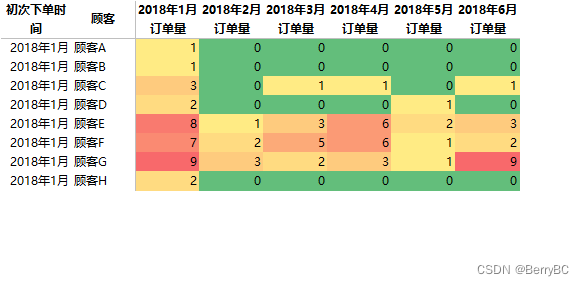
陆拾捌- 如何通过数据影响决策(三)
一、如何正确的引导别人? 引导与误导的区别是什么? 看下面这广告图 单看上面大字的结果,感觉好像真的使用过的人均觉得有好处 可如果我们看下面的细字 对111位连续14天食用(本产品)的燕麦片非重度使用者所做调研… 从…...

VMware 三种网络连接模式
VMware虚拟机的三种网络连接模式:桥接,NAT,仅主机。 网卡vmnet0,vmnet1,vmnet8区别。 在VMware中,虚拟机的网络连接主要是由VMware创建的虚拟交换机负责实现的,VMware可以根据需要创建多个虚拟网络。 VMware的虚拟网…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...
