二分类问题的解决利器:逻辑回归算法详解(一)
文章目录
- 🍋引言
- 🍋逻辑回归的原理
- 🍋逻辑回归的应用场景
- 🍋逻辑回归的实现
🍋引言
逻辑回归是机器学习领域中一种重要的分类算法,它常用于解决二分类问题。无论是垃圾邮件过滤、疾病诊断还是客户流失预测,逻辑回归都是一个强大的工具。本文将深入探讨逻辑回归的原理、应用场景以及如何在Python中实现它。
🍋逻辑回归的原理
逻辑回归是一种广义线性模型(Generalized Linear Model,简称GLM),它的目标是根据输入特征的线性组合来预测二分类问题中的概率。具体来说,逻辑回归通过使用Sigmoid函数(又称为Logistic函数)将线性输出映射到0到1之间的概率值。Sigmoid函数的数学表达式如下:
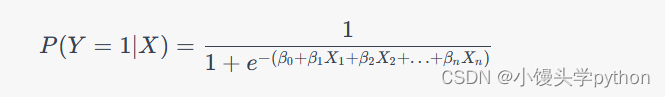
其中, P ( Y = 1 ∣ X ) P(Y=1|X) P(Y=1∣X) 表示在给定输入特征X的条件下,目标变量Y等于1的概率。 β 0 , β 1 , … , β n \beta_0, \beta_1, \ldots, \beta_n β0,β1,…,βn 是模型的权重参数, X 1 , X 2 , … , X n X_1, X_2, \ldots, X_n X1,X2,…,Xn 是输入特征。
逻辑回归的训练目标是找到最佳的权重参数,使得模型的预测结果与实际观测值尽可能一致。这通常通过最大化似然函数或最小化对数损失函数来实现。
🍋逻辑回归的应用场景
逻辑回归在各个领域都有广泛的应用,以下是一些常见的场景:
-
垃圾邮件检测: 逻辑回归可以根据邮件的内容和特征来预测一封邮件是否是垃圾邮件。
-
医学诊断: 在医学领域,逻辑回归可以用于预测患者是否患有某种疾病,基于患者的临床特征和实验室检测结果。
-
金融风险管理: 逻辑回归可用于评估客户违约的概率,帮助银行和金融机构做出信贷决策。
-
社交网络分析: 逻辑回归可以用于社交网络中的用户行为分析,例如预测用户是否会点击广告或关注某个话题。
🍋逻辑回归的实现
这里我们准备封装一个逻辑回归的py文件,命名为LogisticRegression.py
这里我们首先需要导入需要的库
from sklearn.metrics import accuracy_score
import numpy as np
accuracy_score函数用于计算分类模型的准确率,它是一个评估分类模型性能的常用指标。准确率表示正确分类的样本数量占总样本数量的比例。在机器学习中,通常希望模型的准确率越高越好,因为它衡量了模型对数据的分类能力。
之后我们定义一个LogisticRegression类,接下来的代码,我们将写在此类中
首先是初始化函数
def __init__(self):"""初始化LinearRegression模型"""self.coef_ = None # 系数self.interception_ = None # 截距self._theta = None
self.coef_ = None
创建了一个对象属性coef_,并将其初始化为None。coef_通常用来存储线性回归模型的系数(也称为权重),这些系数用于预测目标变量。在初始化时,这些系数还没有被计算,因此被设置为None。
self.interception_ = None
创建了一个对象属性interception_,并将其初始化为None。interception_通常用来存储线性回归模型的截距,也就是模型在特征值为零时的预测值。在初始化时,截距也还没有被计算,因此被设置为None。
self._theta = None
最后一行代码创建了一个对象属性_theta,同样初始化为None。这个属性可能用于存储模型的参数(系数和截距),但是它以一个下划线 _ 开头,这通常表示该属性是类内部使用的,不应该直接被外部访问或修改。
之后我们定义一个逻辑回归特有的函数
def sigmoid(self, t):return 1 / (1 + np.exp(-t))
这个函数用来计算Sigmoid函数的值。Sigmoid函数的数学表达式如下:

其中, t t t 是输入参数。函数使用NumPy库中的np.exp()函数计算 e e e的负t次方,然后将1除以这个结果,得到Sigmoid函数的值。Sigmoid函数的输出范围是0到1之间,当 t t t趋向于正无穷时,Sigmoid函数趋近于1,而当 t t t趋向于负无穷时,Sigmoid函数趋近于0。这使得Sigmoid函数在二分类问题中常用于将线性输出映射到概率值。
之后我们定义fit函数用于训练模型,采用的方法是批量梯度下降来最小化逻辑回归的损失函数,从而找到最优的模型参数,这里我将进行详细说明
def fit(self, x_train, y_train, eta=0.01, n_iters=1e4, epsilon=1e-8):"""根据给定的x_train和y_train 使用梯度下降法训练LogisticRegression模型"""def J(theta, X_b, y): # 计算损失函数J的值,theta是参数y_hat = self.sigmoid(X_b.dot(theta))try:return -np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat)) / len(X_b) # 稍微有点理解迷糊,y真实减去y预测 平方,然后除以个数except:# 返回一个float的最大值return float('inf')def dJ(theta, X_b, y): # theta是一个向量y_hat = self.sigmoid(X_b.dot(theta))return X_b.T.dot(y_hat - y) / len(X_b)def gradient_descent(X_b, y, initial_theta, eta, n_iters, epsilon): # 传入一个最大迭代次数,1万theta = initial_thetaiters = 0while iters < n_iters:gradient = dJ(theta, X_b, y)last_theta = thetatheta = theta - gradient * etaif abs(J(theta, X_b, y) - J(last_theta, X_b, y)).all() < epsilon: # 这里应该是all还是any? 结果好像是一样,不加会报错breakiters += 1return thetaX_b = np.hstack([np.ones((len(x_train), 1)), x_train])# 根据给定的x_train计算出X_binitial_theta = np.zeros(X_b.shape[1])# 创建出一个空的theta向量self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters, epsilon)self.interception_ = self._theta[0]self.coef_ = self._theta[1:]return self
def fit(self, x_train, y_train, eta=0.01, n_iters=1e4, epsilon=1e-8):
这是fit方法的定义,它接受训练数据x_train和对应的目标变量y_train作为输入,还包括三个可选参数:eta(学习率,默认为0.01)、n_iters(最大迭代次数,默认为1万)、epsilon(用于判断收敛的小量值,默认为1e-8)。
def J(theta, X_b, y):
这是一个内部函数,用于计算损失函数的值。传入参数包括模型参数theta、带有偏置项的训练数据X_b,以及目标变量y。损失函数的定义使用了逻辑回归的交叉熵损失函数。
def dJ(theta, X_b, y):
这是另一个内部函数,用于计算损失函数关于参数theta的梯度。梯度是损失函数关于参数的导数,它告诉我们在当前参数值下,损失函数增加最快的方向。这里使用了逻辑回归的梯度计算公式。
def gradient_descent(X_b, y, initial_theta, eta, n_iters, epsilon):
这是用于执行梯度下降法的内部函数。它接受训练数据X_b、目标变量y、初始参数initial_theta、学习率eta、最大迭代次数n_iters以及收敛判定值epsilon。在循环中,它计算梯度并更新参数,直到满足停止条件(收敛或达到最大迭代次数)。
X_b = np.hstack([np.ones((len(x_train), 1)), x_train])
这一行代码创建了一个新的特征矩阵X_b,通过在训练数据前面添加一列全为1的列来实现,以处理截距项。
initial_theta = np.zeros(X_b.shape[1])
这一行代码创建了一个初始的参数向量initial_theta,并将其初始化为全零向量。
self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters, epsilon)
这一行代码调用了gradient_descent函数,使用梯度下降法来训练模型并获得最优的参数向量self._theta。
self.interception_ = self.theta[0]
self.coef = self.theta[1:]
这两行代码将参数向量self.theta中的第一个元素作为截距项赋值给self.interception,将其余的元素作为系数赋值给self.coef。
return self
最后,fit方法返回模型对象自身,以便进行链式操作。
这里我们再定义一个随机梯度下降
def fit_sgd(self, X_train, y_train, n_iters=5, t0=5, t1=50): # 这里的n_iters代表 整个数据看几轮,不能取10000assert X_train.shape[0] == y_train.shape[0]def dJ_sgd(theta, X_b_i, y_i): # 计算梯度,不需要m了,因为是随机挑选出一行数据return X_b_i.T.dot(X_b_i.dot(theta) - y_i) * 2def sgd(X_b, y, initial_theta, n_iters, t0=5, t1=50): # 随机梯度下降法def learning_rate(t):return t0 / (t + t1)theta = initial_thetam = len(X_b)for cur_iter in range(n_iters): random_indexs = np.random.permutation(m) # 随机打乱样本X_b_new = X_b[random_indexs]y_new = y[random_indexs]for i in range(m):gradient = dJ_sgd(theta, X_b_new[i], y_new[i])theta = theta - gradient * learning_rate(cur_iter * m + i)return thetaX_b = np.hstack([np.ones((len(X_train), 1)), X_train])initial_theta = np.random.randn(X_b.shape[1])self._theta = sgd(X_b, y_train, initial_theta, n_iters, t0=5, t1=50)self.interception_ = self._theta[0]self.coef_ = self._theta[1:]
def fit_sgd(self, X_train, y_train, n_iters=5, t0=5, t1=50):
这是fit_sgd方法的定义,与之前的方法不同,它使用随机梯度下降来训练模型。接受训练数据X_train和对应的目标变量y_train,以及可选的参数:n_iters(迭代轮数,默认为5,表示整个数据集会被遍历5次)、t0 和 t1(用于计算学习率的超参数,默认分别为5和50)。
assert X_train.shape[0] == y_train.shape[0]
这一行代码用于确保训练数据X_train和目标变量y_train的样本数量一致,以避免数据维度不匹配的问题。
def dJ_sgd(theta, X_b_i, y_i):
这是一个内部函数,用于计算随机梯度下降的梯度。传入参数包括模型参数 theta、一个样本的特征向量 X_b_i,以及对应的目标变量 y_i。梯度计算使用了逻辑回归的梯度公式,但仅针对单个样本。
def sgd(X_b, y, initial_theta, n_iters, t0=5, t1=50):
这是执行随机梯度下降的内部函数。它接受特征矩阵 X_b、目标变量 y、初始参数 initial_theta、迭代轮数 n_iters,以及学习率计算的超参数 t0 和 t1。
learning_rate(t) 是一个学习率调度函数,根据当前迭代轮数 t 来计算学习率。学习率在每轮迭代中都会发生变化,起初较大,后来逐渐减小,这有助于随机梯度下降的收敛。
随机梯度下降的主要循环包括迭代整个数据集 n_iters 次。在每次迭代中,首先对样本进行随机打乱(打乱顺序),然后遍历每个样本,计算梯度并更新参数。
X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
这一行代码与之前类似,将原始特征矩阵 X_train 转换为带有截距项的特征矩阵 X_b。
initial_theta = np.random.randn(X_b.shape[1])
这一行代码创建了一个随机初始化的参数向量 initial_theta,用作随机梯度下降的起点。
self._theta = sgd(X_b, y_train, initial_theta, n_iters, t0=5, t1=50)
这一行代码调用了 sgd 函数来执行随机梯度下降,训练模型,并获取最优的参数向量 self._theta。
self.interception_ = self.theta[0]
self.coef = self.theta[1:]
这两行代码将参数向量 self.theta 中的第一个元素作为截距项赋值给 self.interception,将其余的元素作为系数赋值给 self.coef。
最后我们进行预测的处理
def predict_prob(self, X_predict):X_b = np.hstack([np.ones((len(X_predict), 1)), X_predict])return self.sigmoid(X_b.dot(self._theta))def predict(self, X_predict):return np.array(self.predict_prob(X_predict) >= 0.5, dtype='int')def score(self, x_predict, y_test):y_predict = self.predict(x_predict)return accuracy_score(y_test, y_predict)def __repr__(self):return "LogisticRegression()"predict_prob(self, X_predict):
这个方法用于对输入的特征数据 X_predict 进行预测,并返回预测的概率值。首先,它将输入数据 X_predict 扩展为带有截距项的特征矩阵 X_b,然后使用模型的参数 _theta 和 sigmoid 函数来计算每个样本的概率值。这个方法返回的是每个样本属于正类别的概率值,范围在0到1之间。
predict(self, X_predict):
这个方法使用 predict_prob 方法返回的概率值来进行二分类预测。它将概率值与阈值0.5进行比较,如果概率值大于等于0.5,则预测为正类别(1),否则预测为负类别(0)。返回的结果是一个包含0和1的数组,表示每个样本的预测类别。
score(self, x_predict, y_test):
这个方法用于评估模型的性能。它接受输入数据 x_predict 和对应的真实目标变量 y_test,并使用 predict 方法来进行预测。然后,它计算模型的准确率(Accuracy)分数,通过与真实标签进行比较来确定模型的预测精度。最终,这个方法返回模型的准确率作为性能评估的指标。
repr(self):
这是一个特殊方法,用于定义模型对象的字符串表示。当您创建模型对象并尝试打印它时,将返回该字符串,以便更好地描述模型。在这里,字符串表示简单地返回了 “LinearRegression()”,表示这是一个线性回归模型。
接下来我们用鸢尾花数据进行实践一下
首先还是导入库
from sklearn.datasets import load_iris
from LogisticRegression import LogisticRegression
import numpy as np
之后做一些前期数据选择,分割数据集的准备
iris = load_iris()
y = iris.target
X = iris.data[y<2,:2]
y = y[y<2]
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
X_train,X_test,y_train,y_test = train_test_split(X,y)
运行结果如下
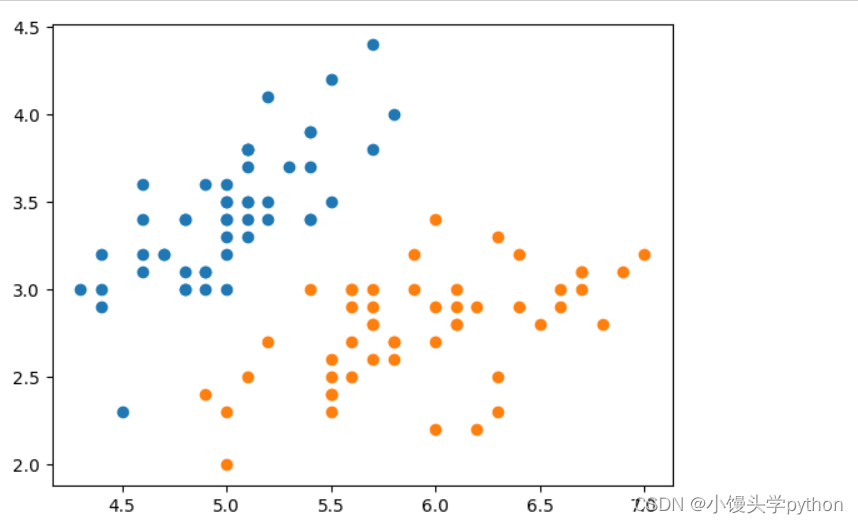
之后我们进行拟合预测
log_reg = LogisticRegression()
log_reg.fit(X_train,y_train)
log_reg.score(X_test,y_test)
运行结果如下

之后我们创建一个用于可视化模型决策会边界的函数
def x2(clf,x1):return (-clf.interception_-x1*clf.coef_[0])/clf.coef_[1]
并绘制图像
x_plot = np.linspace(4,7,100)
y_plot = x2(log_reg,x_plot)
plt.plot(x_plot,y_plot,color='r')
plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()
plt.scatter(X[y == 0,0], X[y == 0,1]) 和 plt.scatter(X[y == 1,0], X[y == 1,1]):
这两行代码用于绘制数据点的散点图。第一行绘制了属于类别0的数据点,第二行绘制了属于类别1的数据点。这样,你可以在图中看到不同类别的数据点的分布情况。
运行结果如下
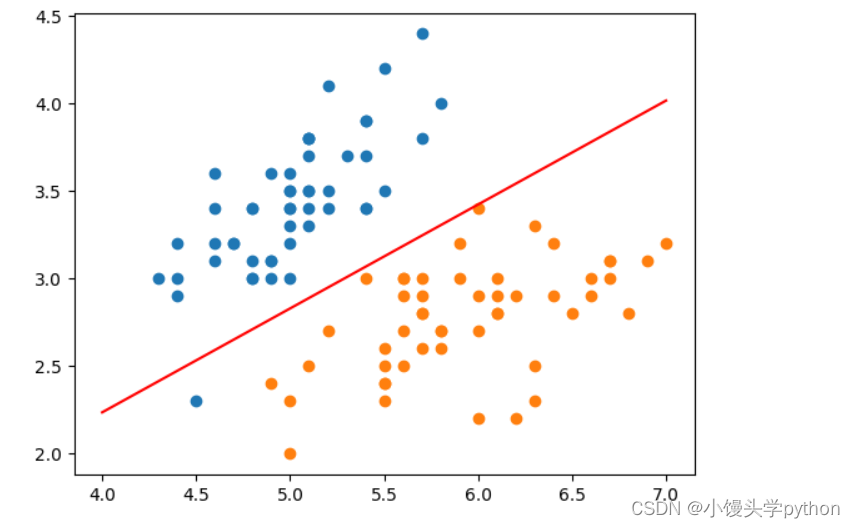
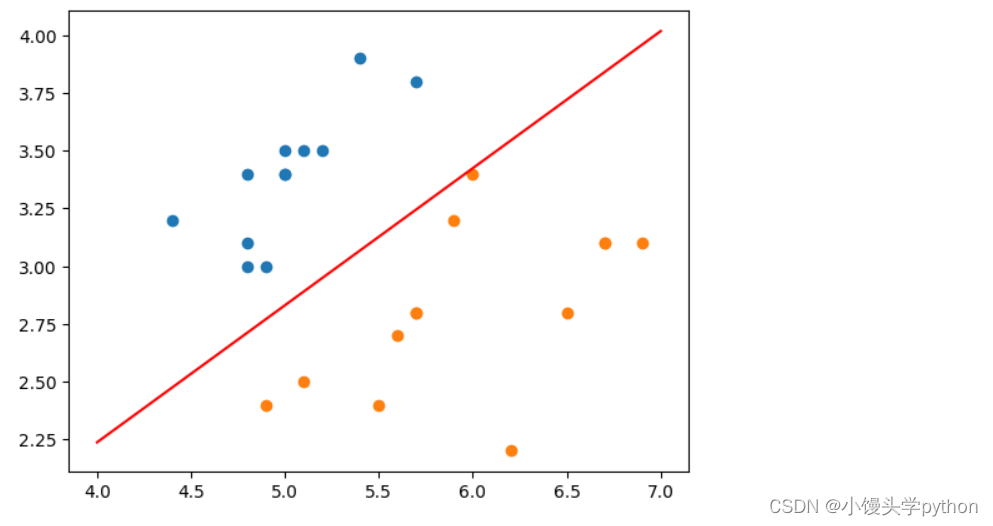
接下来我们用测试集来演示一下
plt.plot(x_plot,y_plot,color='r')
plt.scatter(X_test[y_test==0,0],X_test[y_test==0,1])
plt.scatter(X_test[y_test==1,0],X_test[y_test==1,1])
plt.show()

挑战与创造都是很痛苦的,但是很充实。
相关文章:

二分类问题的解决利器:逻辑回归算法详解(一)
文章目录 🍋引言🍋逻辑回归的原理🍋逻辑回归的应用场景🍋逻辑回归的实现 🍋引言 逻辑回归是机器学习领域中一种重要的分类算法,它常用于解决二分类问题。无论是垃圾邮件过滤、疾病诊断还是客户流失预测&…...

docker alpine镜像中遇到 not found
1.问题: docker alpine镜像中遇到 sh: xxx: not found 例如 # monerod //注:此可执行文件已放到/usr/local/bin/ sh: monerod: not found2.原因 由于alpine镜像使用的是musl libc而不是gnu libc,/lib64/ 是不存在的。但他们是兼容的&…...

python的多线程多进程与多协程
python的多线程是假多线程,本质是交叉串行,并不是严格意义上的并行,或者可以这样说,不管怎么来python的多线程在同一时间有且只有一个线程在执行(举个例子,n个人抢一个座位,但是座位就这一个,不…...

一文介绍使用 JIT 认证后实时同步用户更加优雅
首先本次说的 JIT 指的是 Just In Time ,可以理解为及时录入,一般用在什么样的场景呢? 还记的上次我们说过关于第三方组织结构同步的功能实现,主要目的是将第三方源数据同步到内部平台中来,方便做管控和处理 此处的管…...

搞定“项目八怪”,你就是管理高手!
大家好,我是老原。 玛丽.弗列特说:“权力已经逐渐被视为一个群体的组合能力。我们通过有效联系获取力量。” 有效联系也就是指的沟通,这个部分占据我们项目经理工作内容的80%,可见沟通在项目管理中的重要性。 项目经理的沟通包…...
机器视觉-标定篇
3D结构光标定 结构光视觉的优点: 非接触、信息量大、测精度高、抗干扰能力强。 结构光视觉传感器参数的标定包括:摄像机参数标定、结构光平面参数标定。 结构光视觉测量原理图 我们不考虑镜头的畸变,将相机的成像模型简化为小孔成像模型…...

linux离线安装make
一、下载rpm包 https://pkgs.org/search/?qmake 二、拷贝至服务器 三、安装make rpm -ivh make-3.82-24.el7.x86_64.rpm四、查看是否安装成功 make -v...

【深度学习】卷积神经网络(LeNet)【文章重新修改中】
卷积神经网络 LeNet 前言LeNet 模型代码实现MINST代码分块解析1 构建 LeNet 网络结构2 加载数据集3 初始化模型和优化器4 训练模型5 训练完成 完整代码 Fashion-MINST代码分块解析1 构建 LeNet 网络结构2 初始化模型参数3 加载数据集4 定义损失函数和优化器5 训练模型 完整代码…...
win10 Baichuan2-7B-Chat-4bits 上部署 百川2-7B-对话模型-4bits量化版
搞了两天才搞清楚跑通 好难呢,个人电脑 win10 ,6GB显存 个人感觉 生成速度很慢,数学能力不怎么行 没有ChatGLM2-6B 强,逻辑还行, 要求: 我的部署流程 1.下载模型 ,下载所有文件 然后 放到新建的model目录 https://huggingface.co/baichuan-inc/Baichuan2-7B-Chat-4bits/tr…...
2023/9/20总结
maven maven本质是 一个项目管理工具 将项目开发 和 管理过程 抽象成 一个项目对象模型(POM) POM (Project Object Model) 项目对象模型 作用 项目构建 提供标准的自动化 项目构建 方式依赖管理 方便快捷的管理项目依赖的资源…...

【Git】git 分支或指定文件回退到指定版本
目录 一、分支回滚 1. 使用 git reset 命令 2.使用 git revert 命令 3.使用 git checkout 命令 二、某个文件回滚 1.查看哪些文件发生修改 2.然后查看提交记录(最近几次提交) 3.执行提交命令 一、分支回滚 1. 使用 git reset 命令 命令可以将当前分支的 HEAD 指针指向指…...
Java 消息策略的实现 - Kafak 是怎么设计的
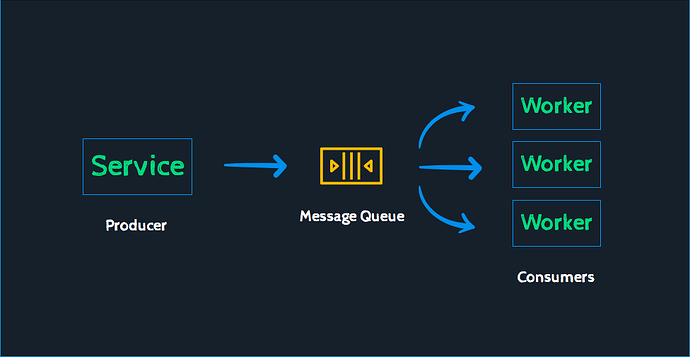
这个也是开放讨论题,主要讨论下 Kafka 在消息中是如何进行实现的。 1_cCyPNzf95ygMFUgsrleHtw976506 21.4 KB 总结 这个题目的开发性太强了。 Kafka 可以用的地方非常多,我经历过的项目有 Kafka 用在消息处理策略上的。这个主要是 IoT 项目,…...
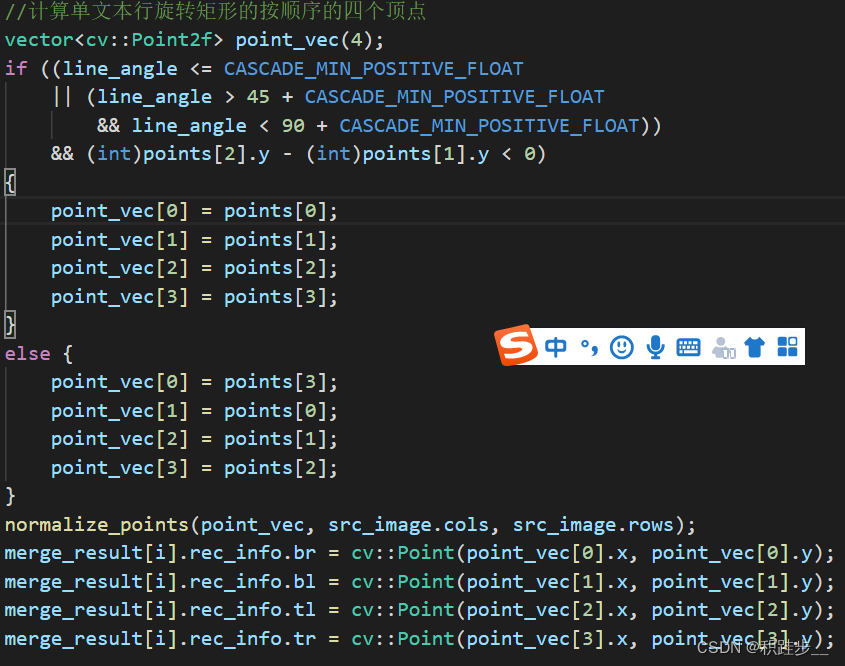
c++opencv RotatedRect 旋转矩形角度转换和顶点顺序转换
这里写自定义目录标题 以下代码记录主要是完成轮廓点求解最小外接矩形之后计算该文本行的角度和旋转矩形的左下(bl),左上(tl),右上(tr),右下(br)的坐标点。 RotatedRect rtminAreaRect(contours…...
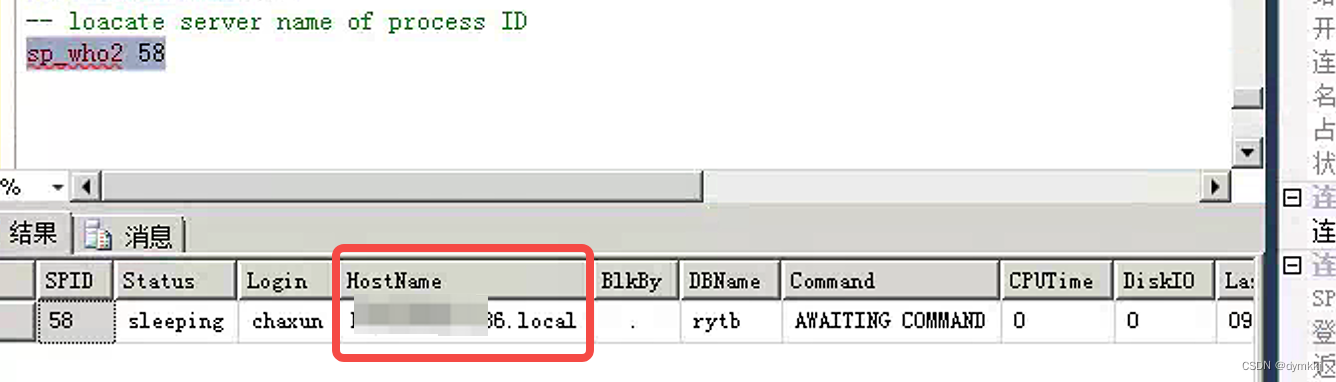
Flink-CDC 抽取SQLServer问题总结
Flink-CDC 抽取SQLServer问题总结 背景 flink-cdc 抽取数据到kafka 中,使用flink-sql进行开发,相关问题总结flink-cdc 配置SQLServer cdc参数 1.创建CDC 使用的角色, 并授权给其查询待采集数据数据库 -- a.创建角色 create role flink_role;-- b.授权…...
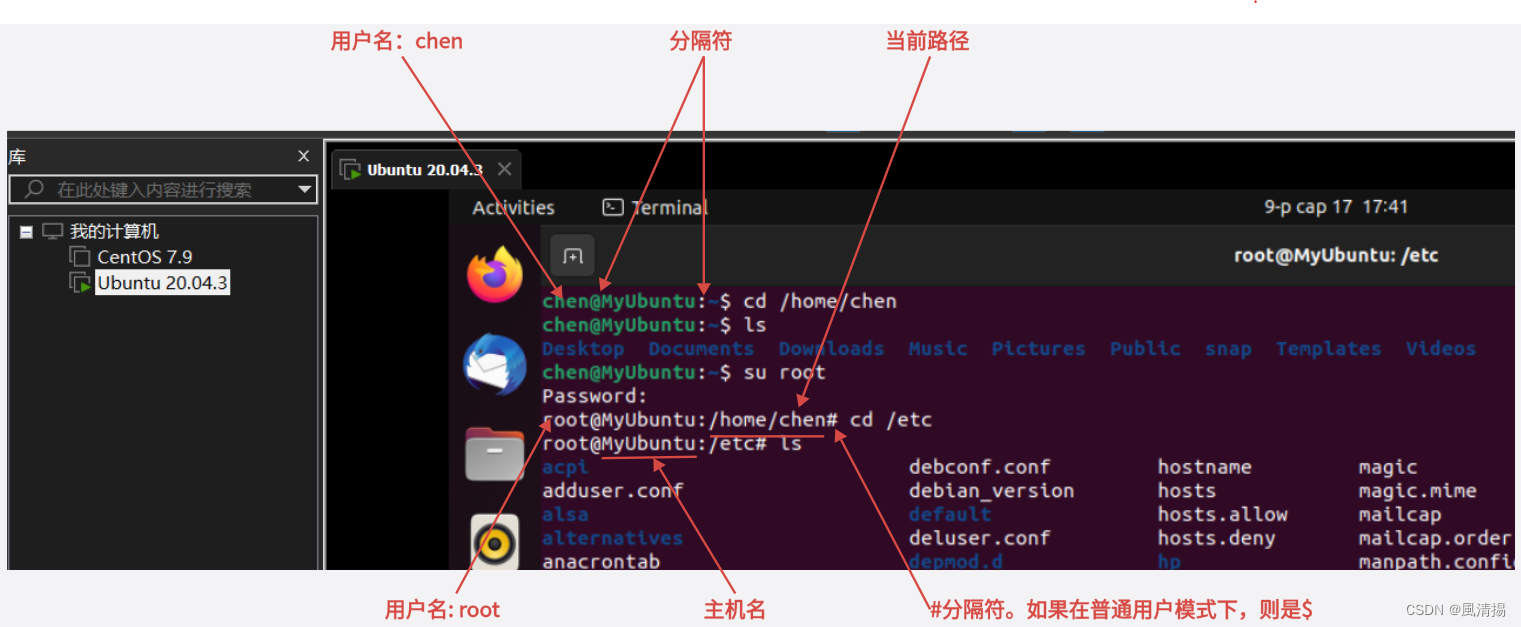
Linux 系统目录结构 终端
系统目录结构 Linux 或 Unix 操作系统中,所有文件和目录呈一个以根节点为始的倒置的树状结构。文件系统的最顶层是根目录,用 / 来表示根目录。在根目录之下的既可以是目录,也可以是文件,而每一个目录中又可以包含子目录文件。如此…...

Layui + Flask | 实现注册、登录功能(案例篇)(08)
此案例内容比较多,建议滑到最后点击阅读原文,阅读体验更佳。后续也会录制案例视频,将在本周内上传到同名的 b 站账号。 已经看了 layui 表单相关的知识,接下来就可以实现注册功能,功能逻辑如下: 项目创建 新建 flask 项目下载 layui 文件,解压之后复制到指定文件编写前…...

GitLab数据迁移后出现500错误
一、背景 去年做GitLab数据迁移时,写过一篇文章《GitLab的备份与还原》。后来发现新创建的项目没问题,但对于迁移过来的项目,修改名称等信息,或者删除该项目时,会出现500错误,以为是系统问题&#…...
音乐随行,公网畅享,群辉Audiostation给你带来听歌新体验!
文章目录 本教程解决的问题是:按照本教程方法操作后,达到的效果是本教程使用环境:1 群晖系统安装audiostation套件2 下载移动端app3 内网穿透,映射至公网 很多老铁想在上班路上听点喜欢的歌或者相声解解闷儿,于是打开手…...

机器学习入门:从算法到实际应用
机器学习入门:从算法到实际应用 机器学习入门:从算法到实际应用摘要引言机器学习基础1. 什么是机器学习?2. 监督学习 vs. 无监督学习 机器学习算法3. 线性回归4. 决策树和随机森林 数据准备和模型训练5. 数据预处理6. 模型训练与调优 实际应用…...

【Vue.js】vue-cli搭建SPA项目并实现路由与嵌套路由---详细讲解
一,何为SPA SPA(Single Page Application)是一种 Web 应用程序的开发模式,它通过使用 AJAX 技术从服务器异步加载数据,动态地更新页面内容,实现在同一个页面内切换不同的视图,而无需整页刷新 1.…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

字符串哈希+KMP
P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...
