角度回归——角度编码方式
文章目录
- 1.为什么研究角度的编码方式?
- 1.1 角度本身具有周期性
- 1.2 深度学习的损失函数因为角度本身的周期性,在周期性的点上可能产生很大的Loss,造成训练不稳定
- 1.3 那么如何处理边界问题呢:(以θ的边界问题为例)
- 1.3 顺时针(CW)
- 1.4 逆时针(CCW)
- 2 角度回归的方式
- 2.1 长边定义法,强制W<H,range范围 [-90,+90)
- 2.3 长边定义135度
- 2.4 OpenCV旧版本定义法
- 2.5 OpenCV新版本定义法
- 不同编码方式之间的转化
- 4 各种表示方法的边界问题
- 参考:
1.为什么研究角度的编码方式?
从框的形式划分,可分为水平检测和旋转检测(即DOTA数据集比赛的task2和task1)。遥感目标检测难点主要包括小目标(small objects)、密集(cluttered arrangement)、方向任意(arbitary orientations)。
1.1 角度本身具有周期性
[ b x , b y , b w , b h , b a n g l e ] [{bx},{by},{bw},{bh},{bangle}] [bx,by,bw,bh,bangle] and [ b x , b y , b w , b h , b a n g l e + π ] [{bx},{by},{bw},{bh},{bangle+π}] [bx,by,bw,bh,bangle+π] 可以表征相同的旋转矩形框
[ b x , b y , b w , b h , b a n g l e ] [{bx},{by},{bw},{bh},{bangle}] [bx,by,bw,bh,bangle] and [ b x , b y , b h , b w , b a n g l e + π / 2 ] [{bx},{by},{bh},{bw},{bangle+π/2}] [bx,by,bh,bw,bangle+π/2] 可以表征相同的旋转矩形框
1.2 深度学习的损失函数因为角度本身的周期性,在周期性的点上可能产生很大的Loss,造成训练不稳定
由于学习的目标参数具有周期性,在周期变化的边界处会导致损失值突增,因此增大网络的学习难度。这句话可以参考下图进行理解:
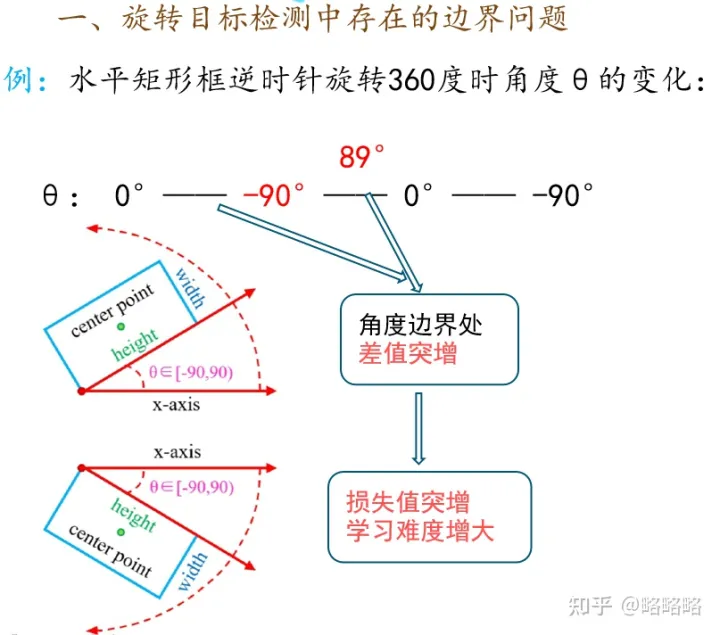
1.3 那么如何处理边界问题呢:(以θ的边界问题为例)
1、寻找一种新的旋转目标定义方式,定义方式中不含具有周期变化性的参数,却又能表示周期旋转的目标物体,根本上杜绝边界问题的产生;(Anchor free/mask的思路,PolarDet、P-RSDet基于极坐标系表示一个任意四边形物体,BBA-Vectors、O^2-DNet基于向量来表示一个有向矩形,ROPDet、Beyond Bounding Box、Oriented Reppoints基于点集来表示一个任意形状的物体,)
2、从损失函数上入手,使用Smooth L1单独考虑每个参数时,赋予损失函数和角度同样的周期性,使得边界处θ之间差值可以很大,但loss变化实际很小;或者综合考虑所有回归参数的影响,使用旋转IoU损失函数也可以规避边界问题,不过RIoU不可导,近似可导的相关工作可以参考KLD、GWD,工程上实现RIoU可导的工作可以参考s2anet/README.md at master · csuhan/s2anet (github.com)
3、θ由回归问题转为分类问题。(把连续问题直接离散化,避开边界情况),当θ变为分类问题后,网络就无法学习到角度距离信息了,比如真实角度为-90,网络预测成89和-89产生的损失值我们期望是一样的,因为角度距离实际上都是1
1.3 顺时针(CW)

1.4 逆时针(CCW)

注:在MMCV中可以设置旋转方向的算子有:box_iou_rotated (默认为CW),nms_rotated (默认为CW),RoIAlignRotated (默认为CCW),RiRoIAlignRotated (默认为CCW)。
2 角度回归的方式
- opencv定义法、
- 长边定义法,
- 四边形定义法
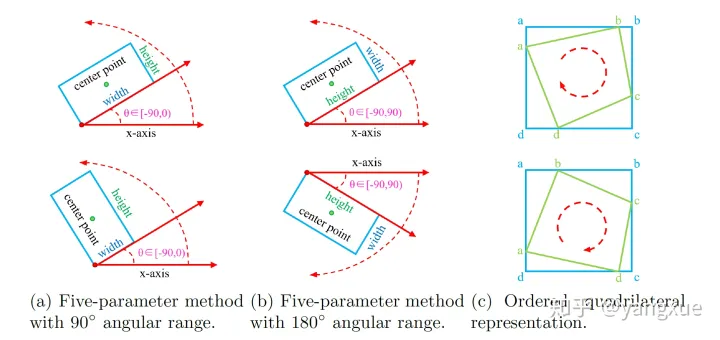

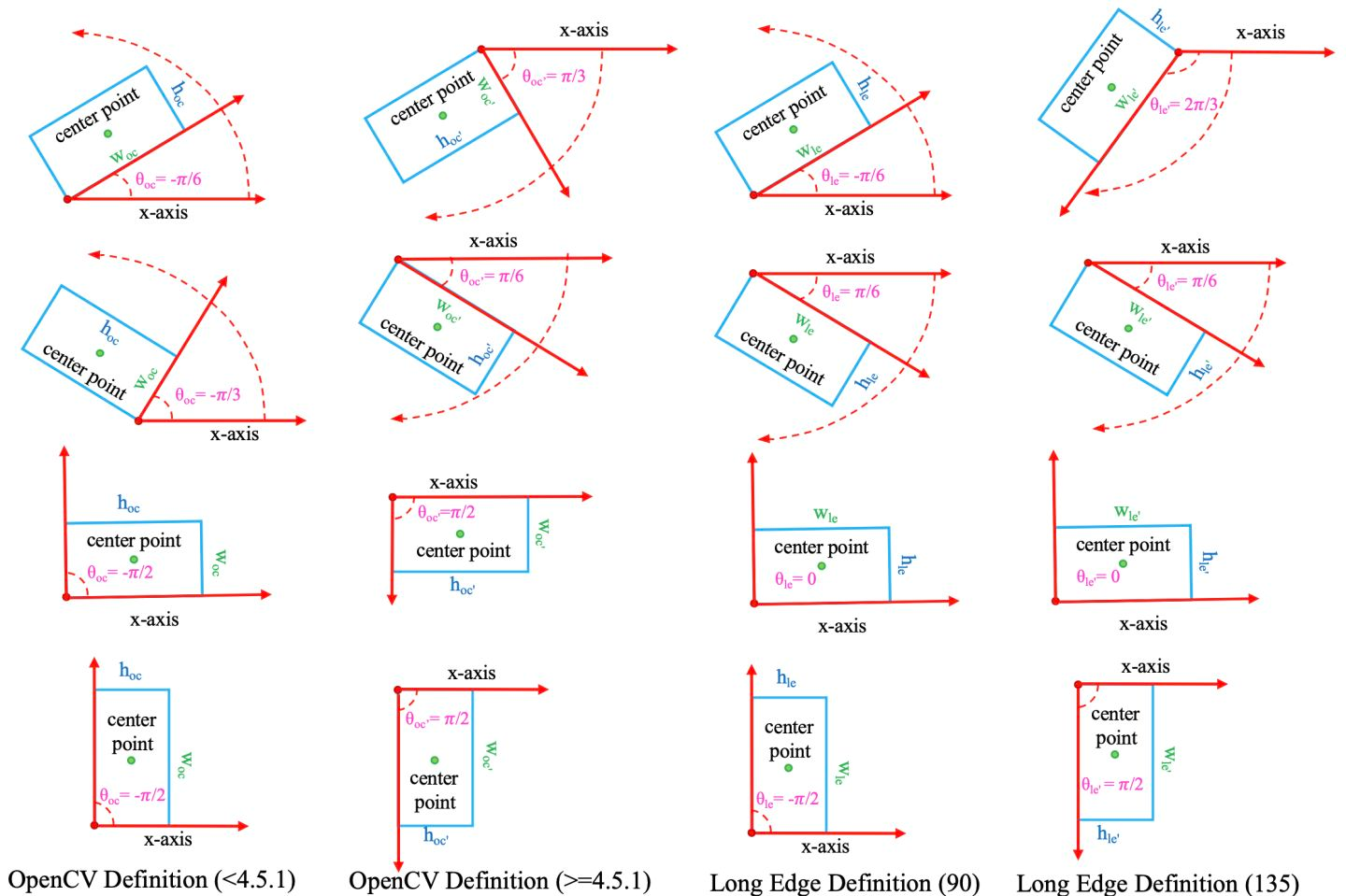
实际上,旋转框既可以由水平框绕在中心点顺时针旋转得到,也可以由水平框绕在中心点逆时针旋转得到。 旋转方向和坐标系的选择密切相关。图像空间采用右手坐标系(y,x) ,其中y轴 是上->下, x轴是左->右。 此时存在2种相反的旋转方向。
2.1 长边定义法,强制W<H,range范围 [-90,+90)
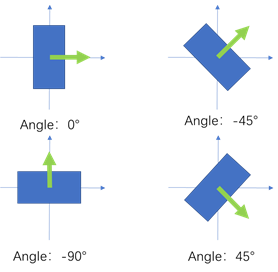

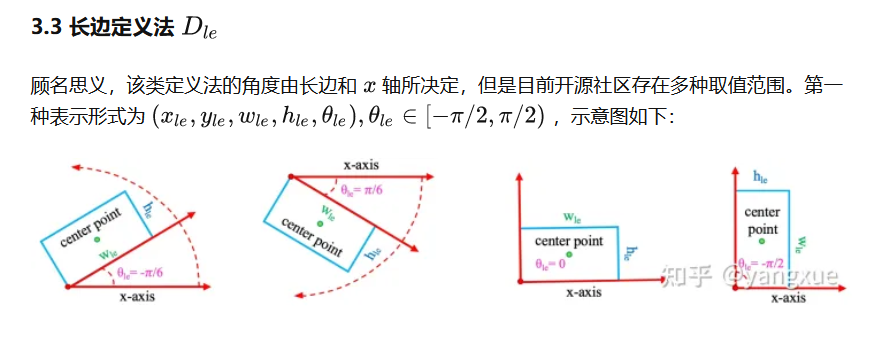
我们采用的是长边定义法,所以我们的注释文件格式为:
[ classid x_c y_c longside shortside Θ ] Θ∈[0, 180)* longside: 旋转矩形框的最长边* shortside: 与最长边对应的另一边* Θ: x轴顺时针旋转遇到最长边所经过的角度
利用好cv2.minAreaRect()函数+总结规律就可以
注意opencv4.1.2版本cv2.minAreaRect()函数生成的最小外接矩形框(x,y,w,h,θ)的几个大坑:
(1) 在绝大数情况下 Θ∈[-90, 0);
(2) 部分水平或垂直的目标边框,其θ值为0;
(3) width或height有时输出0, 与此同时Θ = 90;
(4) 输出的width或height有时会超过图片本身的宽高,即归一化时数据>1。
注意:数据加载器中存在大量的归一化和反归一化的操作,以及大量涉及到图像宽高度的数据变化,因此网络输入的图像size:HEIGHT 必须= WIDTH,因为长边定义法中的longside和shorside与图像的宽高没有严格的对应关系。
数据加载器中涉及三类数据增强方式:Mosaic,random_perspective(仿射矩阵增强),普通数据增强方式。
其中Mosaic,仿射矩阵增强都是针对(X_LT, Y_LT, X_RB, Y_RB)数据格式进行增强,修改时添加θ维度就可以,不过仿射矩阵增强函数内共有 Translation、Shear、Rotation、Scale、Perspective、Center 6种数据增强方式,其中旋转与形变仿射的变换会引起目标角度上的改变。
所以只要超参数中的 [‘perspective’]=0,[‘degrees’]=0 ,这块函数代码就不需要修改逻辑部分,为了方便我们直接把涉及到角度的增强放在最后的普通数据增强方式中。
注意:Mosaic操作中会同时触发MixUp数据增强操作,但是在遥感/无人机应用场景中我个人认为并不适用,首先背景复杂就是该场景中的普遍难题,MixUp会融合两张图像,图像中的小目标会掺杂另一张图的背景信息(包含形似物或噪声),从而影响小目标的特征提取。(不过一切以实验结果为准)
2.3 长边定义135度
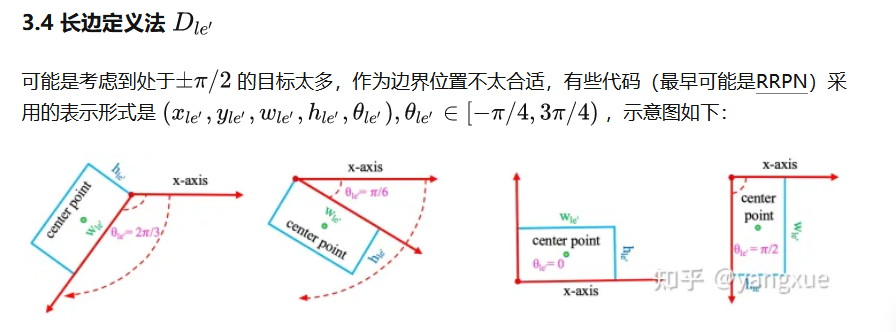
2.4 OpenCV旧版本定义法
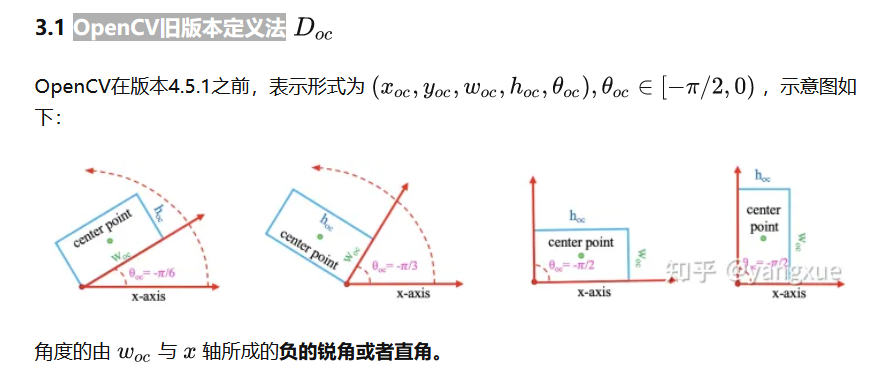
2.5 OpenCV新版本定义法
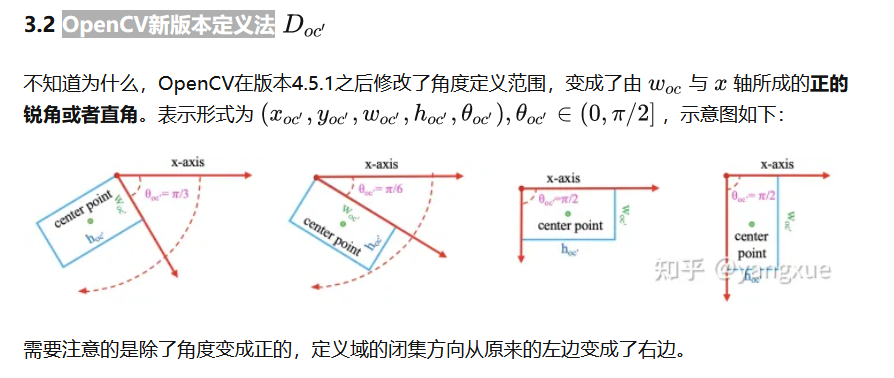
不同编码方式之间的转化
查阅
上面只列了三种转换关系,未列的可以通过这三个进行多步转换或者有兴趣的可以自己总结一下转换关系。不管是哪个表示法的转换,我们可以发现当需要进行变换操作的时候一般是这两种:
边进行交换,同时角度加减 pi/2
边不交换,角度加减 pi
这就很有意思,熟悉GWD论文的朋友可能也回想起不同定义法下的边界问题好像也是这两个关系。我们再来回顾一下为什么高斯建模可以统一不同的定义法和边界问题:
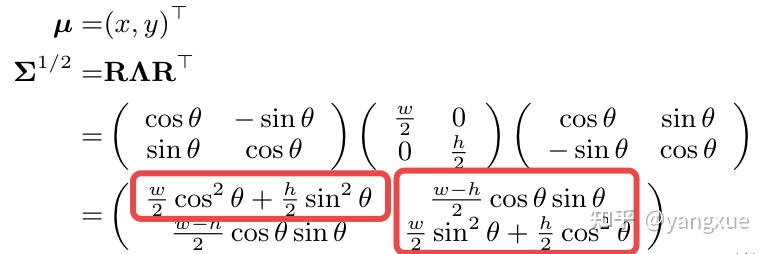
红框中是协方差
中三种不同的元素,这三个元素有一个共同的特点就是经过上面两种变换前后还是相同的,所以高斯建模的优势就在于此。之所以需要三个,那是因为这里有三个参数。抛开高斯分布这个框架,我们是不是可以自己先构造三个这样性质的不同组合,通过直接回归这些参数组合而不是采用GWD和KLD也能成功。
如果再思考得深入一点,我们发现对于不同的表示方式,它们计算IoU的代码其实都是通用的。这是为什么呢?因为IoU的计算过程是和第2节讲的旋转变换有关。在框的旋转过程中我们是不需要考虑旋转角度是怎么定义的,也就不需要担心变换之后是否超过定义范围,逆时针旋转5度对应的就是原始角度减去5度。检测器的参数回归也是这么做的,即使在解码中出现了我们所说的边界问题,其本质还是一个正常的旋转变换。边界问题是针对某一个确定的表示法来说的,因此如果使用IoU损失这种不用考虑框表示方式的损失函数来优化检测器就能完全不用在意边界问题。相同的,高斯建模中的协方差
也存在旋转变换,基于它的回归损失同样不需要考虑定义方式和边界问题。我暂将这种回归损失称为表示方式无关和边界问题免疫。
因此在设计旋转检测器过程中,表示法的作用应该局限于给初始候选框(如anchor)一个初始的表示形式,不能参与回归损失的计算,否则不同表示法和边界问题都会对检测器的优化带来影响,即回归损失应该是表示方式无关和边界问题免疫的。
MMRotate支持 OpenCV、长边135°、长边90° 3 种角度定义法,也支持 DOTA、SSDD、HRSID 3 个遥感数据集。
在OpenMMLab的MMCV中,实现了RiRoIAlignRotated, RotatedFeatureAlign 等高性能旋转框 CUDA 算子,因此 MMRotate 无愧是真正的史上最全、最统一的旋转目标检测算法框架。
4 各种表示方法的边界问题
由于大长宽比的目标对于角度的变化是非常敏感的,因此研究边界问题是比较有意义的。我们希望在边界情况也能预测的比较准确,减少有预测框但是不准被当FP的情况。先给出上面三种定义方法边界问题的描述图:
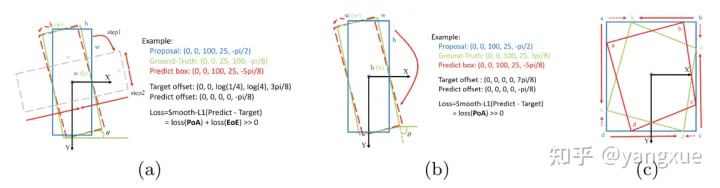
(a)90-regression-based:最理想的角度回归路线是由蓝色框逆时针旋转到红色框,但由于角度的周期性,导致按照这个回归方式的损失非常大(参见上图右边的Example)。此时模型必须以更复杂的形式回归(例如蓝色框顺时针旋转,同时缩放w和h),增加了回归的难度。通过下图(a)右边的example,我们可以发现损失值的突增来源于两部分,一个是角度周期性(periodicity of angular,PoA),另一个是边的交换性(exchangeability of edges,EoE)。
(b) 180-regression-based:相同的,这种方式比上面稍微简单一些,损失值的突增只来源于PoA。
© Point-based: 看©图,如果是蓝框是anchor,红框是ground-truth,那么通过点的排序之后,实际和理想的回归方式是一样的(按照回归的距离定义),都是:

通过上述三种例子的分析,我们不难得出这样的结论:理想的预测结果超出了我们所定义的范围,导致出现边界问题,即产生一个较大的损失值。
参考:
论文:RAPiD Rotation-Aware People Detection in Overhead Fisheye Images
https://zhuanlan.zhihu.com/p/358441134
https://zhuanlan.zhihu.com/p/108185873
https://zhuanlan.zhihu.com/p/111493759
相关文章:

角度回归——角度编码方式
文章目录 1.为什么研究角度的编码方式?1.1 角度本身具有周期性1.2 深度学习的损失函数因为角度本身的周期性,在周期性的点上可能产生很大的Loss,造成训练不稳定1.3 那么如何处理边界问题呢:(以θ的边界问题为例&#x…...

【C# Programming】值类型、良构类型
值类型 1、值类型 值类型的变量直接包含值。换言之, 变量引用的位置就是值内存中实际存储的位置。 2、引用类型 引用类型的变量存储的是对一个对象实例的引用(通常为内存地址)。 复制引用类型的值时,复制的只是引用。这个引用非常小…...
Linux Day18 TCP_UDP协议及相关知识
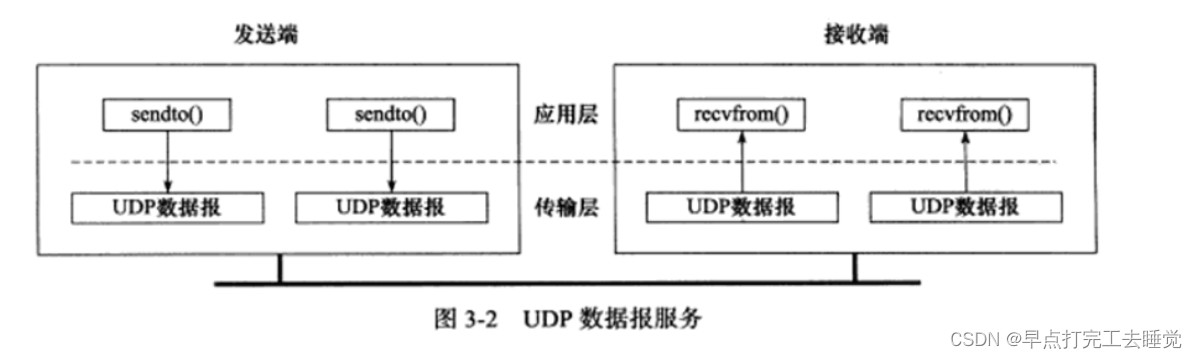
一、网络基础概念 1.1 网络 网络是由若干结点和连接这些结点的链路组成,网络中的结点可以是计算机,交换机、 路由器等设备。 1.2 互联网 把多个网络连接起来就构成了互联网。目前最大的互联网就是因特网。 网络设备有:交换机、路由器、…...

【Java 基础篇】Java网络编程实时数据流处理
在现代计算机应用程序中,处理实时数据流是一项关键任务。这种数据流可以是来自传感器、网络、文件或其他源头的数据,需要即时处理并做出相应的决策。Java提供了强大的网络编程工具和库,可以用于处理实时数据流。本文将详细介绍如何使用Java进…...

Oracle 和 mysql 增加字段SQL
在Oracle和MySQL中,可以使用ALTER TABLE语句来增加字段。下面是分别是两种数据库增加字段的SQL示例: 在Oracle中增加字段的SQL示例: ALTER TABLE 表名ADD (新字段名 数据类型);例如,如果要在名为"employees"的表中添加…...

【脚本】 【Linux】循环执行命令
loop.sh #!/bin/bashif [ "" "$1" ]; thenecho 用法: ./loop.sh 命令内容 时间间隔(毫秒) 循环次数(小于0表示无限循环)echo 示例: ./loop.sh "ps -ef" 1000 10exit 0 fiinterval1000 if [ "" ! "$2" ]; thenif echo &quo…...
快速用Python进行数据分析技巧详解
概要 一些小提示和小技巧可能是非常有用的,特别是在编程领域。有时候使用一点点黑客技术,既可以节省时间,还可能挽救“生命”。 一个小小的快捷方式或附加组件有时真是天赐之物,并且可以成为真正的生产力助推器。所以࿰…...

BD就业复习第二天
Hbase 1. 架构 HBase(Hadoop Database)是一个开源的分布式、面向列族(Column Family)的NoSQL数据库,它是构建在Hadoop之上的。HBase的架构设计旨在处理大规模的数据,特别适用于需要快速读写和随机访问大量…...

大数据Flink(八十五):Window TVF 支持多维数据分析
文章目录 Window TVF 支持多维数据分析 一、Grouping Sets 二、Rollup...

css-边框原理教程
1. CSS中边框原理 他不是一条直线,根据盒子原理,当边框宽度大于元素的长和宽时,呈现一个梯形和三角形的形状,用如下的代码来实地理解一下边框画法实现的原理 注:学习网址: CSS画几种图形的方法_css画图_老…...

【数据结构】时间、空间复杂度
⭐ 作者:小胡_不糊涂 🌱 作者主页:小胡_不糊涂的个人主页 📀 收录专栏:浅谈数据结构 💖 持续更文,关注博主少走弯路,谢谢大家支持 💖 时间、空间复杂度 1. 算法效率3. 时…...

Databend 开源周报第 111 期
Databend 是一款现代云数仓。专为弹性和高效设计,为您的大规模分析需求保驾护航。自由且开源。即刻体验云服务:https://app.databend.cn 。 Whats On In Databend 探索 Databend 本周新进展,遇到更贴近你心意的 Databend 。 理解 SHARE END…...
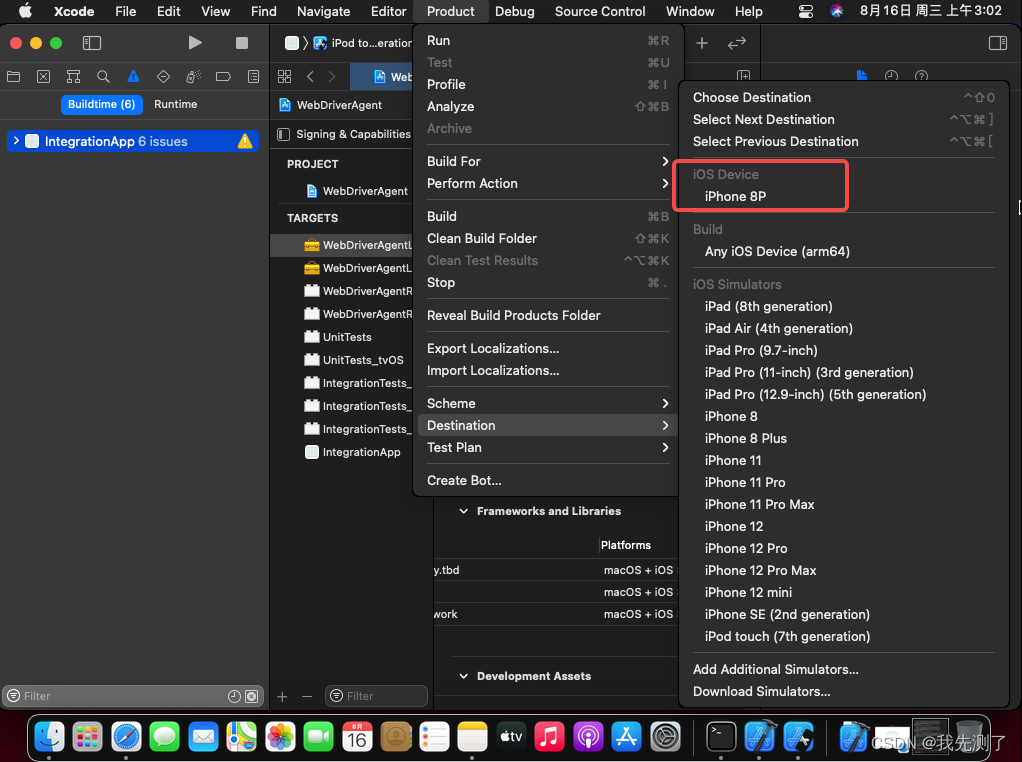
iOS自动化测试方案(一):MacOS虚拟机保姆级安装Xcode教程
文章目录 一、环境准备二、基础软件三、扩展:usb拓展插件 一、环境准备 1、下载VMware虚拟机的壳子,安装并注册软件(可以百度注册码),最新版本:v17 2、下MacOS系统iOS镜像文件,用于vmware虚拟机安装,当前镜…...

vue3 - Vue 项目处理GitHub Pages 部署后 _plugin-vue_export-helper.js 404
GitHub Demo 地址 在线预览 vue3项目打包后部署到github pages 后,预览网站提示下划线开头的一个文件_plugin-vue_export-helper访问不到,网络请求显示404 处理GitHub Pages 部署 _plugin-vue_export-helper.js 404 https://github.com/rollup/rollup/b…...
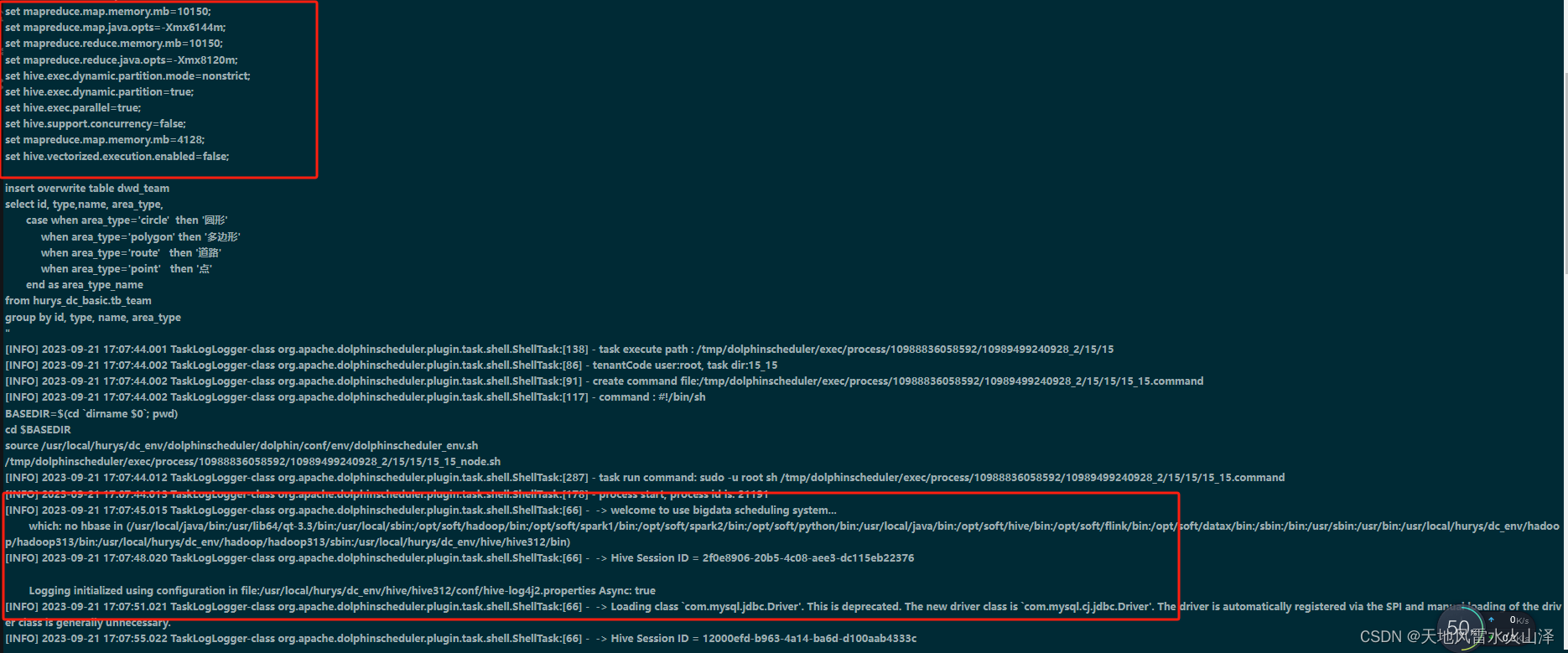
一百八十一、Hive——海豚调度HiveSQL任务时当Hive的计算引擎是mr或spark时脚本的区别(踩坑,附截图)
一、目的 当Hive的计算引擎是spark或mr时,发现海豚调度HQL任务的脚本并不同,mr更简洁 二、Hive的计算引擎是Spark时 (一)海豚调度脚本 #! /bin/bash source /etc/profile nowdatedate --date0 days ago "%Y%m%d" y…...
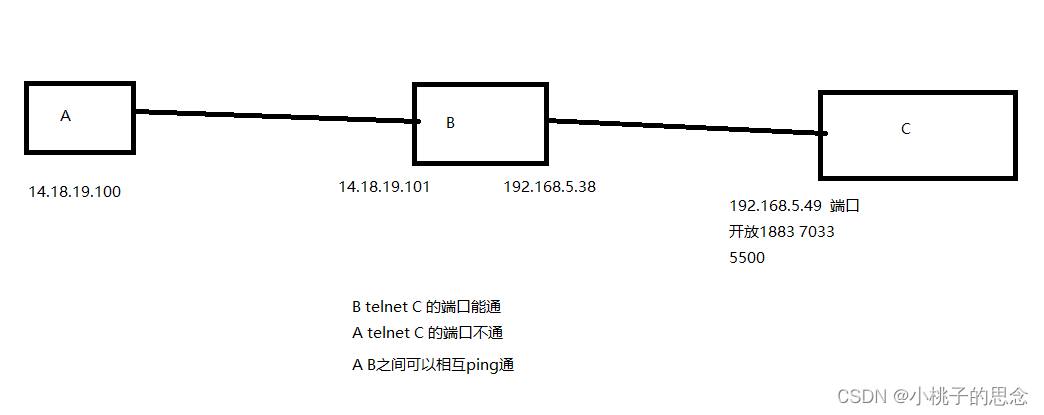
Linux 隔离网段下端口转发
设备在隔离网段下,设置端口转发。使A设备可访问C设备的服务 #!/bin/bash #输出成绩脚本 echo -n "请输入外网服务器的IP地址:" read score sudo iptables -t nat -A PREROUTING -p tcp --dport 1883 -j DNAT --to-destination $score:1883 s…...

【CDN和UDN】CDN和UDN技术特点以及使用场景
内容分发网络(CDN)和用户自定义网络(UDN)是两种不同的网络技术,在选择时,往往不能准备把握具不同的技术特点和应用场景。CDN 主要用于加速内容分发,而 UDN 则主要用于支持用户自定义的网络需求。…...

【Linux】改变缓存路径、清理缓存
写在前面 在做项目的过程中,服务器base路径下空间不足,准备在另一个目录下创建虚拟环境,但在安装的过程中,发现base路径下的空间还是在减少,后来经过学习了解到,pip安装下载依赖包时,会先下载缓…...

python+opencv寻找图片或视频中颜色进行追踪之HSV颜色处理
pythonopencv寻找图片或视频中颜色进行追踪之HSV颜色处理 1.颜色空间转换 import cv2img cv2.imread(1.jpg) # 转换为灰度图 img_gray cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)cv2.imshow(img, img) cv2.imshow(gray, img_gray) cv2.waitKey(0)cv2.cvtColor()用来进行颜色模…...
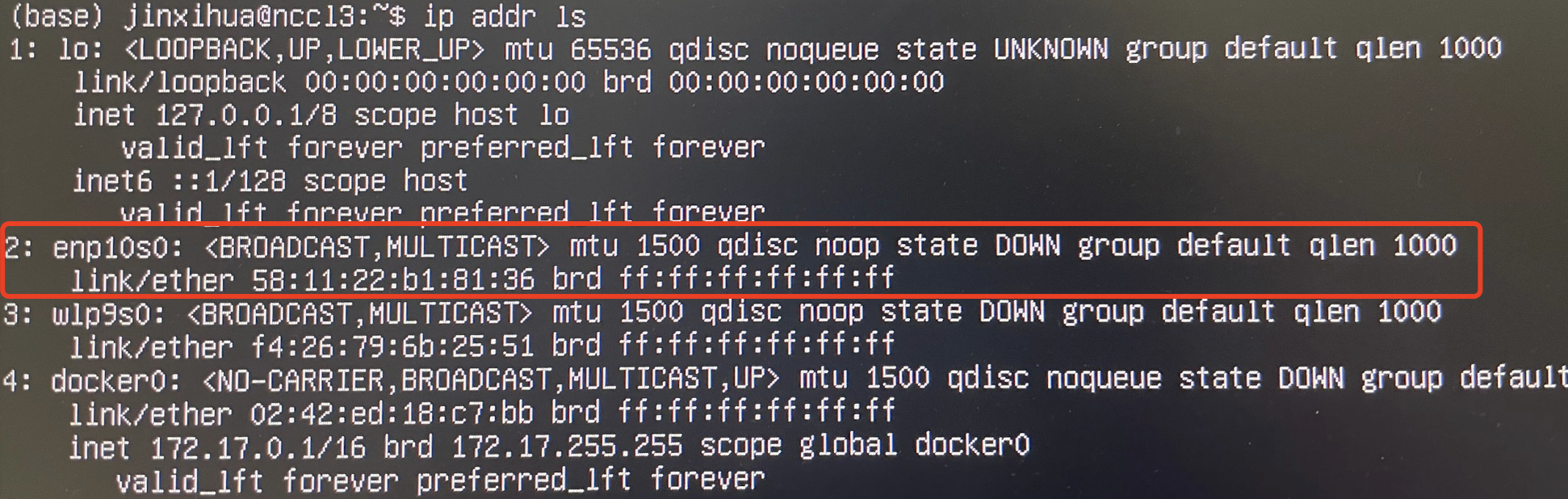
ubuntu 22.04 服务器网卡无IP地址
ssh连接服务器连接不上,提示如下; 连接显示器,ip addr ls 命令查看IP地址,有网卡但没有IP地址 solution: sudo dhclient enp10s0用于通过 DHCP 协议获取网络配置信息并为名为 enp10s0 的网络接口分配 IP 地址,enp1…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...
