Leetcode.2522 将字符串分割成值不超过 K 的子字符串
题目链接
Leetcode.2522 将字符串分割成值不超过 K 的子字符串
rating : 1605
题目描述
给你一个字符串 s s s ,它每一位都是 1 1 1 到 9 9 9 之间的数字组成,同时给你一个整数 k k k 。
如果一个字符串 s s s 的分割满足以下条件,我们称它是一个 好 分割:
- s s s 中每个数位 恰好 属于一个子字符串。
- 每个子字符串的值都小于等于 k k k 。
请你返回 s s s 所有的 好 分割中,子字符串的 最少 数目。如果不存在 s s s 的 好 分割,返回 − 1 -1 −1 。
注意:
- 一个字符串的 值 是这个字符串对应的整数。比方说,
"123"的值为 $1234 ,"1"的值是 1 1 1 。 - 子字符串 是字符串中一段连续的字符序列。
示例 1:
输入:s = “165462”, k = 60
输出:4
解释:我们将字符串分割成子字符串 “16” ,“54” ,“6” 和 “2” 。每个子字符串的值都小于等于 k = 60 。
不存在小于 4 个子字符串的好分割。
示例 2:
输入:s = “238182”, k = 5
输出:-1
解释:这个字符串不存在好分割。
提示:
- 1 ≤ s . l e n g t h ≤ 1 0 5 1 \leq s.length \leq 10^5 1≤s.length≤105
- s [ i ] s[i] s[i] 是
'1'到'9'之间的数字。 - 1 ≤ k ≤ 1 0 9 1 \leq k \leq 10^9 1≤k≤109
解法一 : 动态规划
我们定义 f ( i ) f(i) f(i) 为 s s s 的前 i i i 个字符中,好分割的最少个数。按照定义,最终我们返回的答案就是 f ( n ) f(n) f(n)。
那么我们很容易就能得出状态转移方程:
f [ j ] = m a x ( f [ j ] , f [ i ] + 1 ) ( s [ i + 1 , j ] ≤ k , i < j ) f[j] = max(f[j] , f[i] + 1) \qquad (s[i + 1,j] \leq k , i < j) f[j]=max(f[j],f[i]+1)(s[i+1,j]≤k,i<j)
由于 k ≤ 1 0 9 k \leq 10^9 k≤109,所以 j − i j - i j−i 最大就是 9 9 9。
时间复杂度: O ( n × 9 ) O(n \times 9) O(n×9)
C++代码:
class Solution {
public:int minimumPartition(string s, int k) {int n = s.size();vector<int> f(n + 1,1e9);f[0] = 0;for(int i = 0;i <= n;i++){int len = min(n , i + 9) , sum = 0;for(int j = i + 1;j <= len;j++){sum = sum * 10 + (s[j - 1] - '0');if(sum > k) break;f[j] = min(f[i] + 1 , f[j]);}}//for(int i = 1;i <= n;i++) cout<<f[i]<<" ";return f[n] == 1e9 ? -1 : f[n];}
};
解法二:贪心
我们每次分割的时候,让 好分割 尽可能的大,剩下的子串就更少,所能得到的 好分割 也就越少。
所以贪心策略就是,每次分割的时候让 好分割 尽可能地大,这样最终的答案就是最少的。
时间复杂度: O ( n ) O(n) O(n)
C++代码:
using LL = long long;class Solution {
public:int minimumPartition(string s, int k) {int n = s.size() , ans = 0;for(int i = 0;i < n;i++){//可能会溢出 所以要用 long longLL sum = 0;int j = i;for(;j < n;j++){if((s[j] - '0') > k) return -1;sum = sum * 10 + (s[j] - '0');if(sum > k) break;}ans++;i = j - 1;}return ans;}
};
相关文章:

Leetcode.2522 将字符串分割成值不超过 K 的子字符串
题目链接 Leetcode.2522 将字符串分割成值不超过 K 的子字符串 rating : 1605 题目描述 给你一个字符串 s s s ,它每一位都是 1 1 1 到 9 9 9 之间的数字组成,同时给你一个整数 k k k 。 如果一个字符串 s s s 的分割满足以下条件,我们…...
)
成绩分析(蓝桥杯)
成绩分析 题目描述 小蓝给学生们组织了一场考试,卷面总分为 100 分,每个学生的得分都是一个 0 到 100 的整数。 请计算这次考试的最高分、最低分和平均分。 输入描述 输入的第一行包含一个整数 n (1≤n≤104 ),表示考试人数。 接下来 n 行…...
【多思路附源码持续更新】2023年华为杯(中国研究生数学建模)竞赛C题
赛题 若官网拥挤,数据集和赛题下载地址如下: https://download.csdn.net/download/weixin_47723732/88364777 历届优秀论文下载地址,可以做参考文章 https://download.csdn.net/download/weixin_47723732/88365222 论文万能模板下载地址 htt…...
)
基于STM32设计的校园一卡通(设计配套的手机APP)
一、功能介绍 【1】项目介绍 随着信息技术的不断发展,校园一卡通作为一种高效便捷的管理方式,已经得到了广泛的应用。而其核心部件——智能卡也被越来越多的使用者所熟知。 本文介绍的项目是基于STM32设计的校园一卡通消费系统,通过RC522模块实现对IC卡的读写操作,利用2…...
有了Spring为什么还需要SpringBoot呢
目录 一、Spring缺点分析 二、什么是Spring Boot 三、Spring Boot的核心功能 3.1 起步依赖 3.2 自动装配 一、Spring缺点分析 1. 配置文件和依赖太多了!!! spring是一个非常优秀的轻量级框架,以IOC(控制反转&…...

【记录】Python 之于 C/C++ 区别
记录本人在 Python 上经常写错的一些地方(C/C 写多了,再写 Python 有点切换不过来) 逻辑判断符号用 and、or、!可以直接 10 < num < 30 比较大小分支语句:if、elif、else使用 、-,Python 中不支持 、- - 这两个…...

【Vue-Element-Admin】dialog关闭回调事件
背景 点击导入按钮,调出导入弹窗,解析excel数据后,不点击【确认并导入】按钮,直接关闭弹窗,数据违背清理 实现 使用dialog的close回调函数,在el-dialog添加close,在methods中定义closeDialog…...

Ansible自动化:简化你的运维任务
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
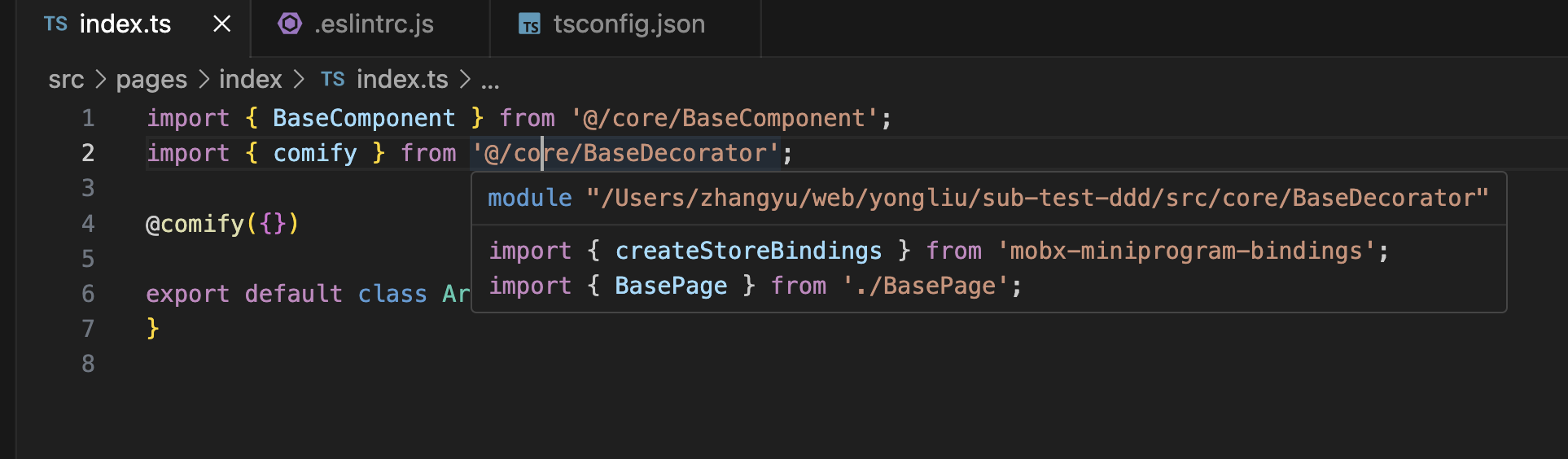
webpack配置alias后eslint和ts无法识别
背景 我们在 webpack 配置 alias 后,发现项目中引入的时候,还是会报错,如下: 可以看到,有一个是 ts报错,还有一个是 eslint 报错。 解决 ts 报错 tsconfig.json {"compilerOptions": {...&q…...
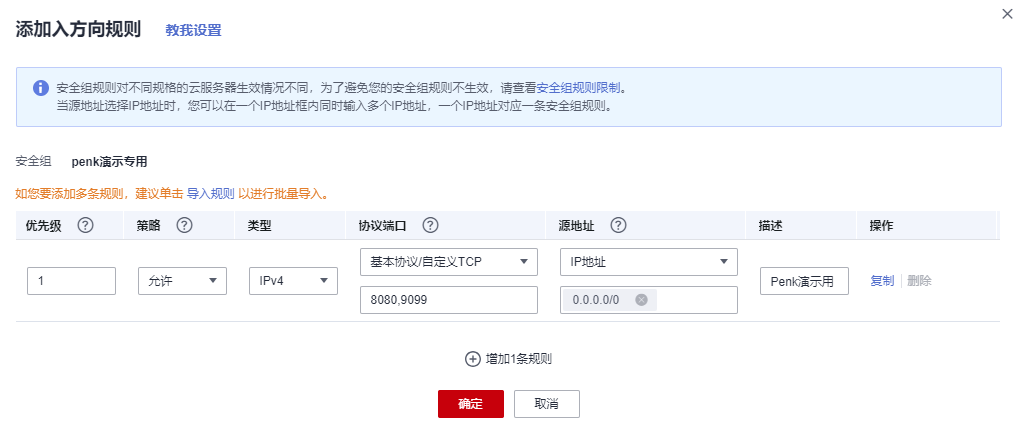
小程序从无到有教学教程-- 01.重置华为云服务器Huawei Cloud EulerOS 2.0版本并且设置安全组
概述 专门拿了专栏来讲解,所以目录结构就比较简单了 文章目录 概述修改华为云操作系统选择Huawei Cloud EulerOS 2.0 镜像顺便配置华为安全组 修改华为云操作系统 这里选择华为最新的系统,不过也就2.0~ 选择Huawei Cloud EulerOS 2.0 镜像 这里记住密…...

js实现短信验证码一键登录
前言 短信验证码一键登录是一种方便快捷的登录方式,用户只需输入手机号码,然后接收到手机短信验证码并自动填入验证码框,即可完成登录操作。本文将介绍短信验证码一键登录的原理,并给出一个简单的示例说明。 短信验证码一键登录…...

vue2的基础知识巩固
一、定义:是一个渐进式的JavaScript框架 二、特点: 减少了大量的DOM操作编写 ,可以更专注于逻辑操作分离数据和界面的呈现,降低了代码耦合度(前端端分离)支持组件化开发,更利于中大型项目的代码组织 vue2核心功能&a…...
echart离线地图下载地址
链接: 离线地图地址 https://datav.aliyun.com/portal/school/atlas/area_selector...

elk日志某个时间节点突然搜索不到了
elk日志某个时间节点突然搜索不到了,检查filebeat正常 Kibana手动上传数据: 响应: Error: Validation Failed: 1: this action would add [2] total shards, but this cluster currently has [2000]/[2000] maximum shards open 原因:ElasticSearch总分片数量导致的异常,ES…...
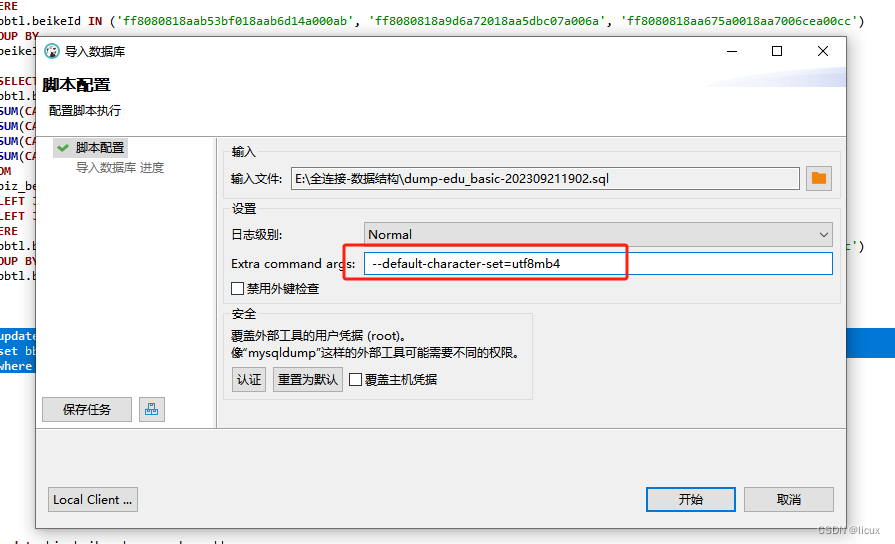
dbeaver 导出的sql文件,恢复数据库报错,Unknown command ‘\‘‘.
这是因为编码格式错误导致的, 加上这个即可 (注意前后不能有空格) --default-character-setutf8mb4...

Android.bp常用语法和预定义属性
介绍 Android.bp是Android构建系统中用于定义模块和构建规则的配置文件,它使用一种简单的声明式语法。以下是Android.bp的一些常见语法规则和约定: 注释: 单行注释使用//符号。 多行注释使用/和/包围。 和go语言相同 // 这是单行注释 /* 这是…...

close和fclose
在Linux系统中,close函数并不会主动调用fsync接口。close函数只是关闭了文件描述符,而不保证数据被写入到磁盘。如果你想确保数据被写入到磁盘,你需要在close函数之前调用fsync函数。这是因为Linux使用了缓存机制来提高磁盘的读写性能&#x…...
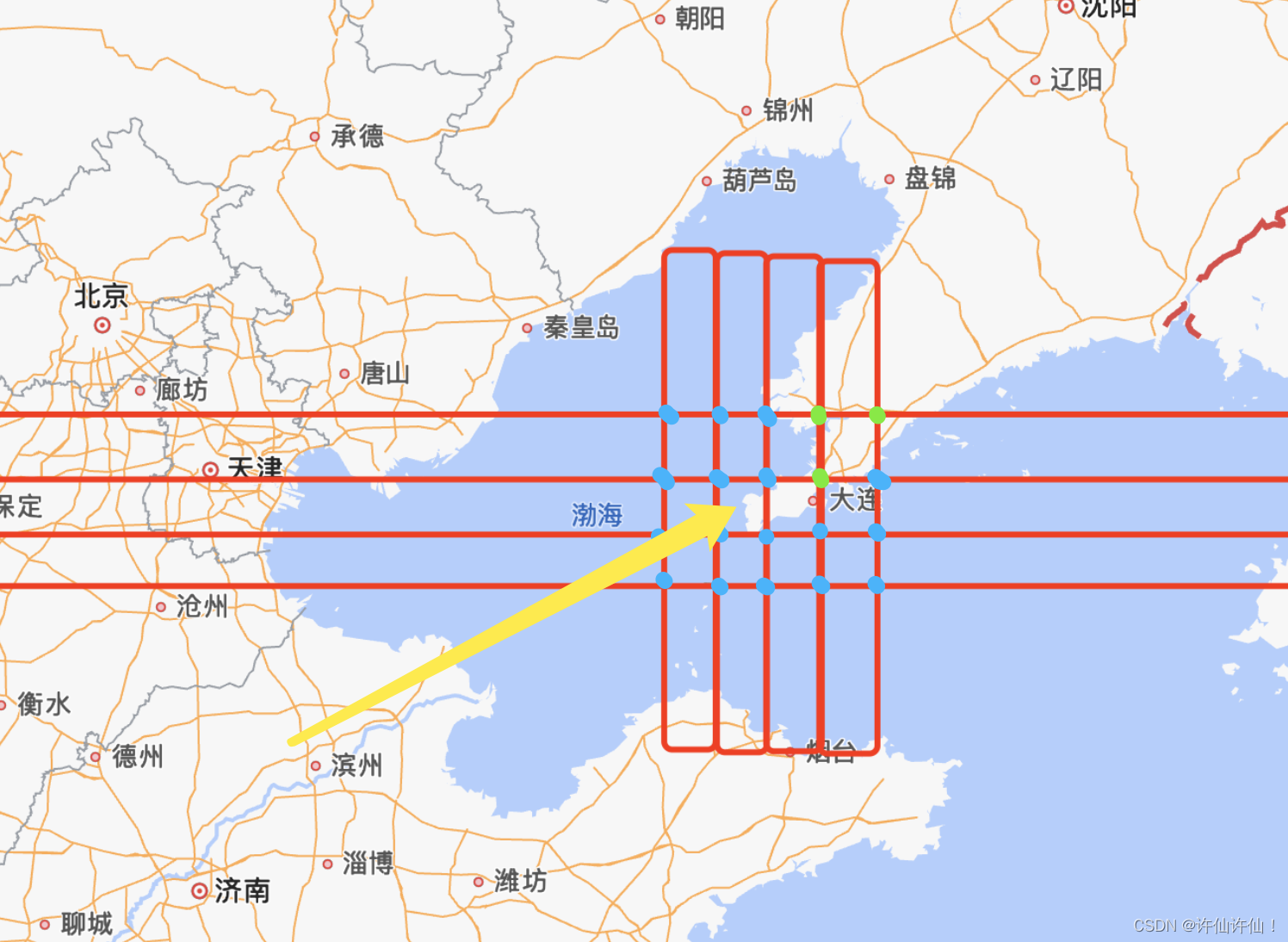
在已知的二维坐标里找到最接近的点
一、业务场景 最近在研发的项目,在做可视化层,在全球地图上,对我们的国家的陆地地图经纬度按照步长为1的间隔做了二维处理。在得到一组整数的点位信息后,需要将我们已有的数据库数据(业务项目)按照地址的经纬度,映射到…...

spring boot 八、 sharding-jdbc 分库分表 按月分表
在项目resources目录下新建com.jianmu.config.sharding.DateShardingAlgorithm 文件 新增yaml配置 数据源 spring:shardingsphere:props:sql:#是否在日志中打印 SQLshow: true#打印简单风格的 SQLsimple: truedatasource:names: pingxuanlogpingxuanlog:type: com.alibaba.dru…...

Java 8 中Stream流的一些用法
public class Djmxlist {private String dxmc;private Integer sl;public String getDxmc() {return dxmc;}public void setDxmc(String dxmc) {this.dxmc dxmc;}public Integer getSl() {return sl;}public void setSl(Integer sl) {this.sl sl;} }插入一下数据 List<Djm…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...

[USACO23FEB] Bakery S
题目描述 Bessie 开了一家面包店! 在她的面包店里,Bessie 有一个烤箱,可以在 t C t_C tC 的时间内生产一块饼干或在 t M t_M tM 单位时间内生产一块松糕。 ( 1 ≤ t C , t M ≤ 10 9 ) (1 \le t_C,t_M \le 10^9) (1≤tC,tM≤109)。由于空间…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...
