2023华为杯研究生数学建模竞赛选题建议+初步分析
如下为C君的2023华为杯研究生数学建模竞赛(研赛)选题建议+初步分析
2023华为杯研究生数学建模竞赛(研赛)选题建议
提示:DS C君认为的难度:C=E<D<F,开放度:C=D=E<F。
华为专项的题目(A、B题)暂不进行选题分析,不太建议大多数同学选择,对自己专业技能有很大自信的可以选择华为专项的题目。后续团队会直接更新A、B题思路,以下为CDEF题选题建议及初步分析:

C题:大规模创新类竞赛评审方案研究
C题是建模+评价类题目。题目需要按照给定的规则对大规模的竞赛做优良的评审方案。
C君觉得这道题不算难,之前训练过大数据、数据分析类题目的同学都可以做。这里简单提一下第一问,第一问需要建立数学模型确定最优的“交叉分发”方案,并讨论该方案的有关指标(自己定义)和实施细节。
这里方案考虑的因素尽量越多越好,有关指标的定义是关键,大家可以一开始想尽量多的指标,然后在后面可以进行相关性分析等算法,对很多的指标进行降重。
这里推荐的算法为拟合类算法和评价类算法。拟合类推荐:
最小二乘法(Least Squares Method):通过最小化观测值与拟合曲线之间的差距来进行拟合,适用于线性和非线性问题。
多项式拟合(Polynomial Fitting):将数据拟合为一个多项式函数,可以通过最小二乘法或牛顿插值法等方法实现。
线性回归(Linear Regression):通过拟合一个线性模型来描述观测值与预测变量之间的关系,可以使用最小二乘法来求解模型参数。
非线性回归(Nonlinear Regression):通过拟合一个非线性模型来描述观测值与预测变量之间的关系,通常需要使用迭代优化算法进行求解,如Levenberg-Marquardt算法。
曲线拟合(Curve Fitting):将数据拟合为一条曲线,可以使用多种拟合函数,如指数函数、对数函数、幂函数等。
插值法(Interpolation):通过已知数据点之间的插值来估计未知数据点的值,常见的插值方法有拉格朗日插值、牛顿插值、样条插值等。
核函数回归(Kernel Regression):通过使用核函数对数据进行加权平滑处理,来实现对非线性关系的拟合。
非参数回归(Nonparametric Regression):不依赖于事先设定的函数形式,而是根据数据的分布进行拟合,常见的方法有局部加权回归、核密度估计等。评价类算法,比如灰色综合评价法、模糊综合评价法对各个指标建立联系。
这道题建议统计学、数学等相关专业同学选择,难度适中,开放度较高。
D题:区域双碳目标与路径规划研究
D题是常见的建模+政策类问题。对于这种问题,建模比赛中经常会遇到,大家可以多去参考往年的其他比赛的相关赛题,很多都是有优秀论文的。
本题需要分析、评价和预测能效提升、产业(产品)升级、能源脱碳和能源消费电气化等重点工程对碳排放的影响。这道题目重点就是如何去找指标,建立对应数学建模,其中题目给了很多限制条件,相对而言这道题目也不算难。
所有专业的同学应该都可以选择这道题目,开放度较高,后续我们也会持续更新思路、代码等的。

E题:出血性脑卒中临床智能诊疗建模
这道题就是很多同学在训练的时候经常做的题目类型了,属于大数据、数据分析类题目,同时也是团队擅长的题目。需要一定的建模能力,和其他赛事赛题类型类似,建议大家(各个专业均可)进行选择。
题目需要通过对真实临床数据的分析,研究出血性脑卒中患者血肿扩张风险、血肿周围水肿发生及演进规律,最终结合临床和影像信息,预测出血性脑卒中患者的临床预后。建立数学模型,大家可以使用评价类算法,比如灰色综合评价法、模糊综合评价法对各个指标建立联系。
第一问前大家需要对数据进行分析和数值化处理,也就是EDA(探索性数据分析)。对于数值型数据,大家用归一化、去除异常值等方式就可以进行数据预处理。而对于非数值型数据进行量化,大家可以使用以下方法:
1标签编码
标签编码是将一组可能的取值转换成整数,从而对非数值型数据进行量化的一种方法。例如,在机器学习领域中,对于一个具有多个类别的变量,我们可以给每个类别赋予一个唯一的整数值,这样就可以将其转换为数值型数据。
2独热编码onehot
独热编码是将多个可能的取值转换成二进制数组的一种方法。在独热编码中,每个可能取值对应一个长度为总共可能取值个数的二进制数组,其中只有一个元素为1,其余元素均为0。例如,对于一个性别变量,可以采用独热编码将“男”和“女”分别转换为[1, 0]和[0, 1]。
3分类计数
分类计数是将非数值型数据转换为数值型数据的一种简单方法。在分类计数中,我们根据某些特定属性(比如学历、职业等)来对数据进行分类,然后统计每个类别的数量或频率。例如,在调查问卷中,我们可以对某个问题的回答按照“是”、“否”和“不确定”三个类别进行分类,并计算每个类别的数量或频率。
4主成分分析
主成分分析是将多维数据转换为低维度表示的一种方法。在主成分分析中,我们通过找到最能解释数据变异的主成分来对原始数据进行降维处理。这样就可以将非数值型数据转换为数值型数据。
而第一问建议大家使用一些可视化方法,可以使用常见的EDA可视化方法:
l 直方图和密度图:展示数值变量的分布情况。
l 散点图:展示两个连续变量之间的关系。
l 箱线图:展示数值变量的分布情况和异常值。
l 条形图和饼图:展示分类变量的分布情况。
l 折线图:展示随时间或顺序变化的趋势。
l 热力图:展示不同变量之间的相关性。
l 散点矩阵图:展示多个变量之间的散点图矩阵。
l 地理图:展示地理位置数据和空间分布信息。
由于和时间序列相关,所以推荐大家使用一些时间序列算法,比如ARIMA等。
由于这篇是选题建议,详细思路可以看我的后续文章/视频。就不赘述了。数据集怎么分析,可视化代码什么的,后续会更新。这道题目开放度较高,难度较易,是本次比赛获奖的首选题目。推荐所有专业同学选择门槛较低且开放度也相对较高。

F题:强对流降水临近预报
F题是数模类赛事很常见的物理类赛题,需要学习不少相关知识。一些数值计算的部分,应该还需要用到运筹学的多目标规划和一些专业相关的算式。
另外题目中提到了一类基于卷积神经网络(Convolutional Neural Networks, CNNs),如U-Net等模型[3];另一类基于循环神经网络(Recurrent Neural Networks, RNNs),如ConvLSTM、DGMR等模型[4, 5]。
代表可能需要用到深度学习的相关知识。另外,建议大家重点关注题目中给到的这些参考文献,建议大家都去阅读检索一下,把能用的都提炼出来。
这道题目建议物理、电气、数学等相关专业同学选择,相对而言门槛较高,小白/非相关专业同学谨慎选择。C君建议在最后对对答案,答案的正确与否会对最终成绩产生较大影响。
其中各题目思路、代码、讲解视频、论文及其他相关内容,可以点击下方群名片哦!
相关文章:

2023华为杯研究生数学建模竞赛选题建议+初步分析
如下为C君的2023华为杯研究生数学建模竞赛(研赛)选题建议初步分析 2023华为杯研究生数学建模竞赛(研赛)选题建议 提示:DS C君认为的难度:CE<D<F,开放度:CDE<F。 华为专项…...

多线程并发或线程安全问题如何解决
1、通过volatile关键字修饰变量,可以实现线程之间的可见性,避免变量脏读的出现,底层是通过限制jvm指令的重新排序实现的,适用于一个线程修改,多个线程读的场景。 2、通过synchronized锁(任意对象࿰…...
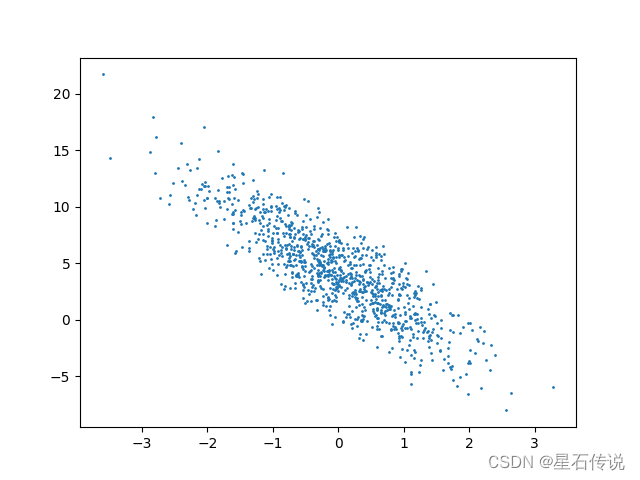
深度学习——线性神经网络一
深度学习——线性神经网络一 文章目录 前言一、线性回归1.1. 线性回归的基本元素1.1.1. 线性模型1.1.2. 损失函数1.1.3. 解析解1.1.4. 随机梯度下降1.1.5. 用模型进行预测 1.2. 向量化加速1.3. 正态分布与平方损失1.4. 从线性回归到深度网络 二、线性回归的从零开始实现2.1. 生…...
利用大模型知识图谱技术,告别繁重文案,实现非结构化数据高效管理
我,作为一名产品经理,对文案工作可以说是又爱又恨,爱的是文档作为嘴替,可以事事展开揉碎讲清道明;恨的是只有一个脑子一双手,想一边澄清需求一边推广宣传一边发布版本一边申报认证实在是分身乏术࿰…...

Java抽象类和普通类区别、 数组跟List的区别
抽象类 Java中的抽象类是一种特殊的类,它不能被实例化,只能被继承。抽象类通常用于定义一些通用的属性和方法,但是这些方法的具体实现需要在子类中完成。抽象类中可以包含抽象方法和非抽象方法。 抽象方法是一种没有实现的方法,…...

Leetcode.2522 将字符串分割成值不超过 K 的子字符串
题目链接 Leetcode.2522 将字符串分割成值不超过 K 的子字符串 rating : 1605 题目描述 给你一个字符串 s s s ,它每一位都是 1 1 1 到 9 9 9 之间的数字组成,同时给你一个整数 k k k 。 如果一个字符串 s s s 的分割满足以下条件,我们…...
)
成绩分析(蓝桥杯)
成绩分析 题目描述 小蓝给学生们组织了一场考试,卷面总分为 100 分,每个学生的得分都是一个 0 到 100 的整数。 请计算这次考试的最高分、最低分和平均分。 输入描述 输入的第一行包含一个整数 n (1≤n≤104 ),表示考试人数。 接下来 n 行…...
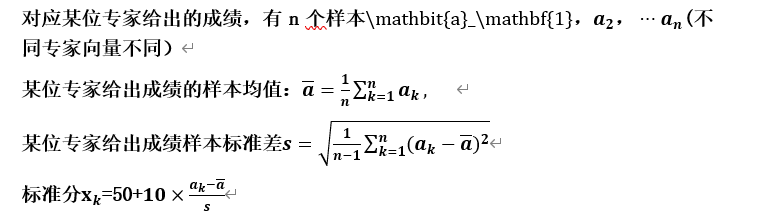
【多思路附源码持续更新】2023年华为杯(中国研究生数学建模)竞赛C题
赛题 若官网拥挤,数据集和赛题下载地址如下: https://download.csdn.net/download/weixin_47723732/88364777 历届优秀论文下载地址,可以做参考文章 https://download.csdn.net/download/weixin_47723732/88365222 论文万能模板下载地址 htt…...
)
基于STM32设计的校园一卡通(设计配套的手机APP)
一、功能介绍 【1】项目介绍 随着信息技术的不断发展,校园一卡通作为一种高效便捷的管理方式,已经得到了广泛的应用。而其核心部件——智能卡也被越来越多的使用者所熟知。 本文介绍的项目是基于STM32设计的校园一卡通消费系统,通过RC522模块实现对IC卡的读写操作,利用2…...
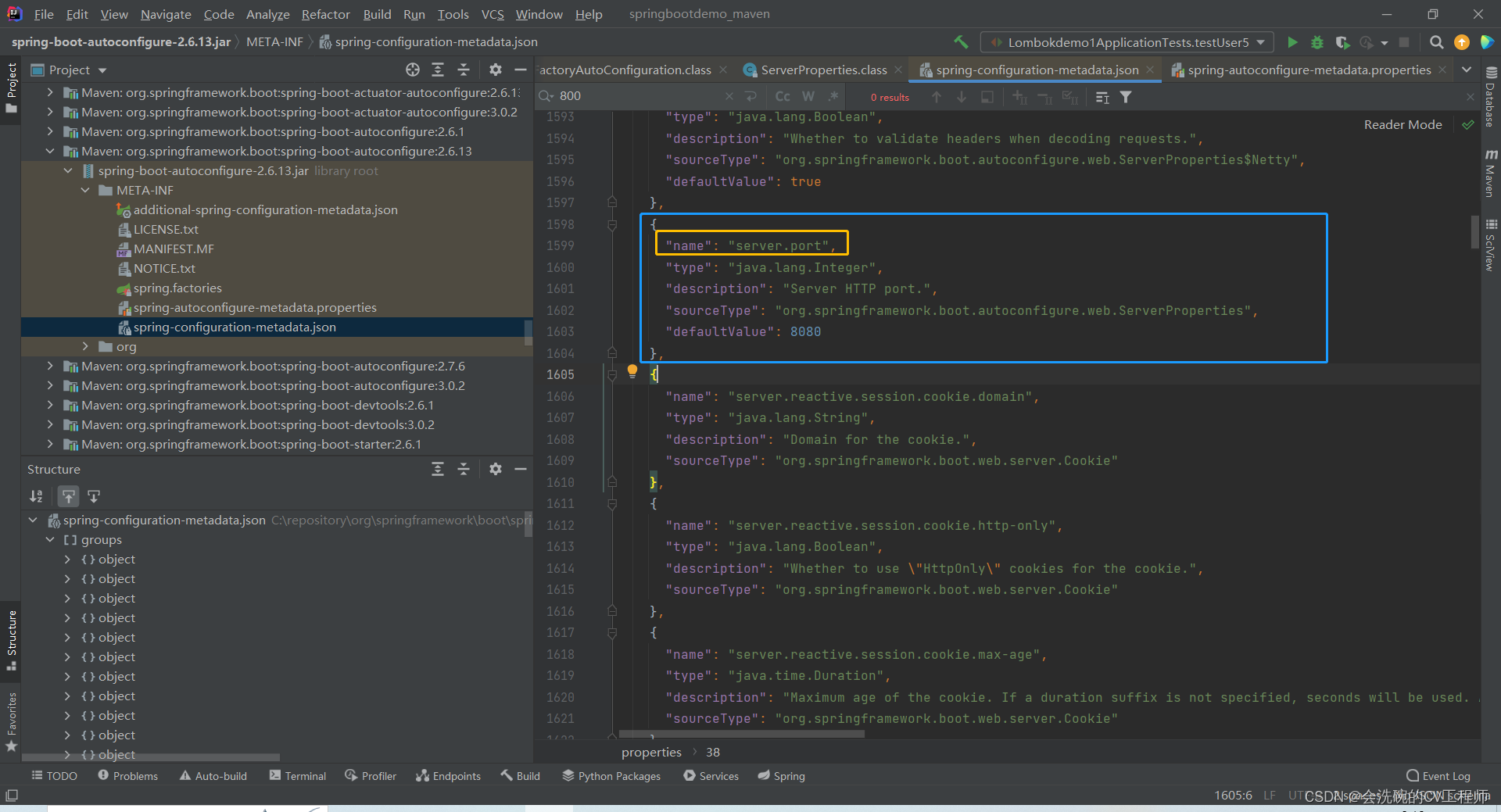
有了Spring为什么还需要SpringBoot呢
目录 一、Spring缺点分析 二、什么是Spring Boot 三、Spring Boot的核心功能 3.1 起步依赖 3.2 自动装配 一、Spring缺点分析 1. 配置文件和依赖太多了!!! spring是一个非常优秀的轻量级框架,以IOC(控制反转&…...

【记录】Python 之于 C/C++ 区别
记录本人在 Python 上经常写错的一些地方(C/C 写多了,再写 Python 有点切换不过来) 逻辑判断符号用 and、or、!可以直接 10 < num < 30 比较大小分支语句:if、elif、else使用 、-,Python 中不支持 、- - 这两个…...

【Vue-Element-Admin】dialog关闭回调事件
背景 点击导入按钮,调出导入弹窗,解析excel数据后,不点击【确认并导入】按钮,直接关闭弹窗,数据违背清理 实现 使用dialog的close回调函数,在el-dialog添加close,在methods中定义closeDialog…...

Ansible自动化:简化你的运维任务
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
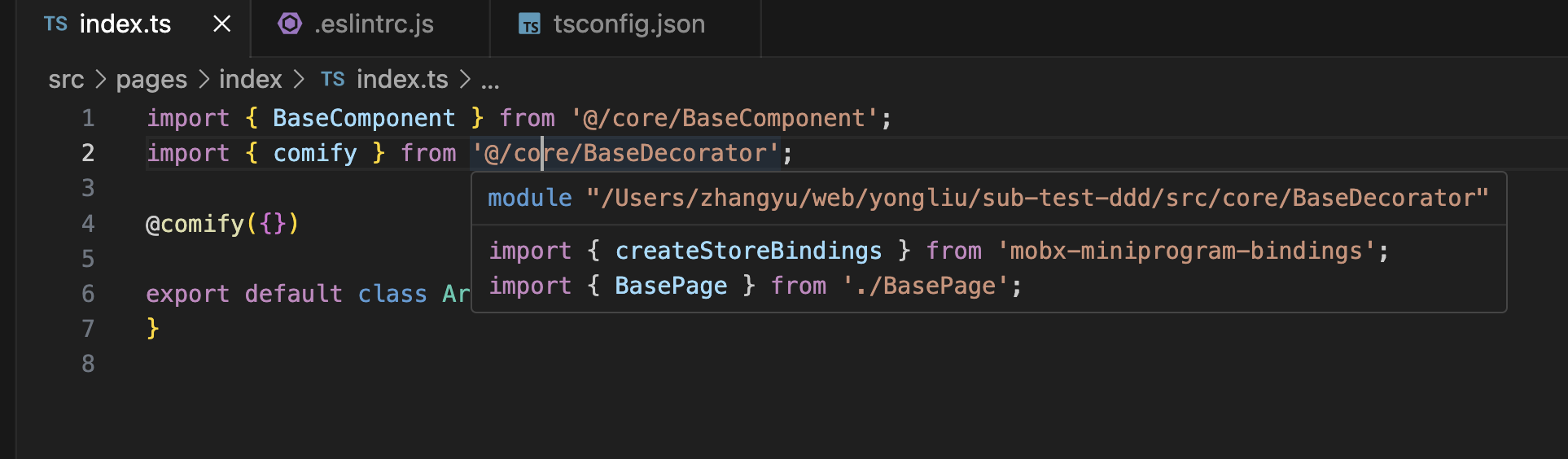
webpack配置alias后eslint和ts无法识别
背景 我们在 webpack 配置 alias 后,发现项目中引入的时候,还是会报错,如下: 可以看到,有一个是 ts报错,还有一个是 eslint 报错。 解决 ts 报错 tsconfig.json {"compilerOptions": {...&q…...
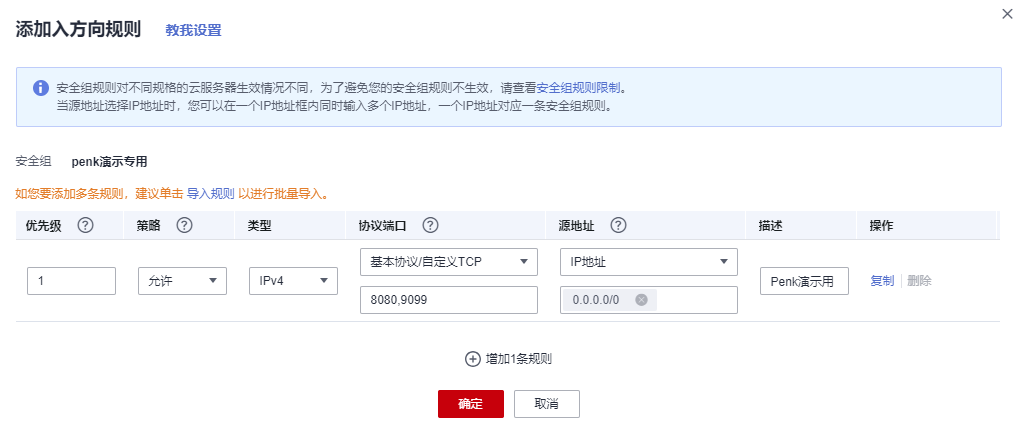
小程序从无到有教学教程-- 01.重置华为云服务器Huawei Cloud EulerOS 2.0版本并且设置安全组
概述 专门拿了专栏来讲解,所以目录结构就比较简单了 文章目录 概述修改华为云操作系统选择Huawei Cloud EulerOS 2.0 镜像顺便配置华为安全组 修改华为云操作系统 这里选择华为最新的系统,不过也就2.0~ 选择Huawei Cloud EulerOS 2.0 镜像 这里记住密…...

js实现短信验证码一键登录
前言 短信验证码一键登录是一种方便快捷的登录方式,用户只需输入手机号码,然后接收到手机短信验证码并自动填入验证码框,即可完成登录操作。本文将介绍短信验证码一键登录的原理,并给出一个简单的示例说明。 短信验证码一键登录…...

vue2的基础知识巩固
一、定义:是一个渐进式的JavaScript框架 二、特点: 减少了大量的DOM操作编写 ,可以更专注于逻辑操作分离数据和界面的呈现,降低了代码耦合度(前端端分离)支持组件化开发,更利于中大型项目的代码组织 vue2核心功能&a…...
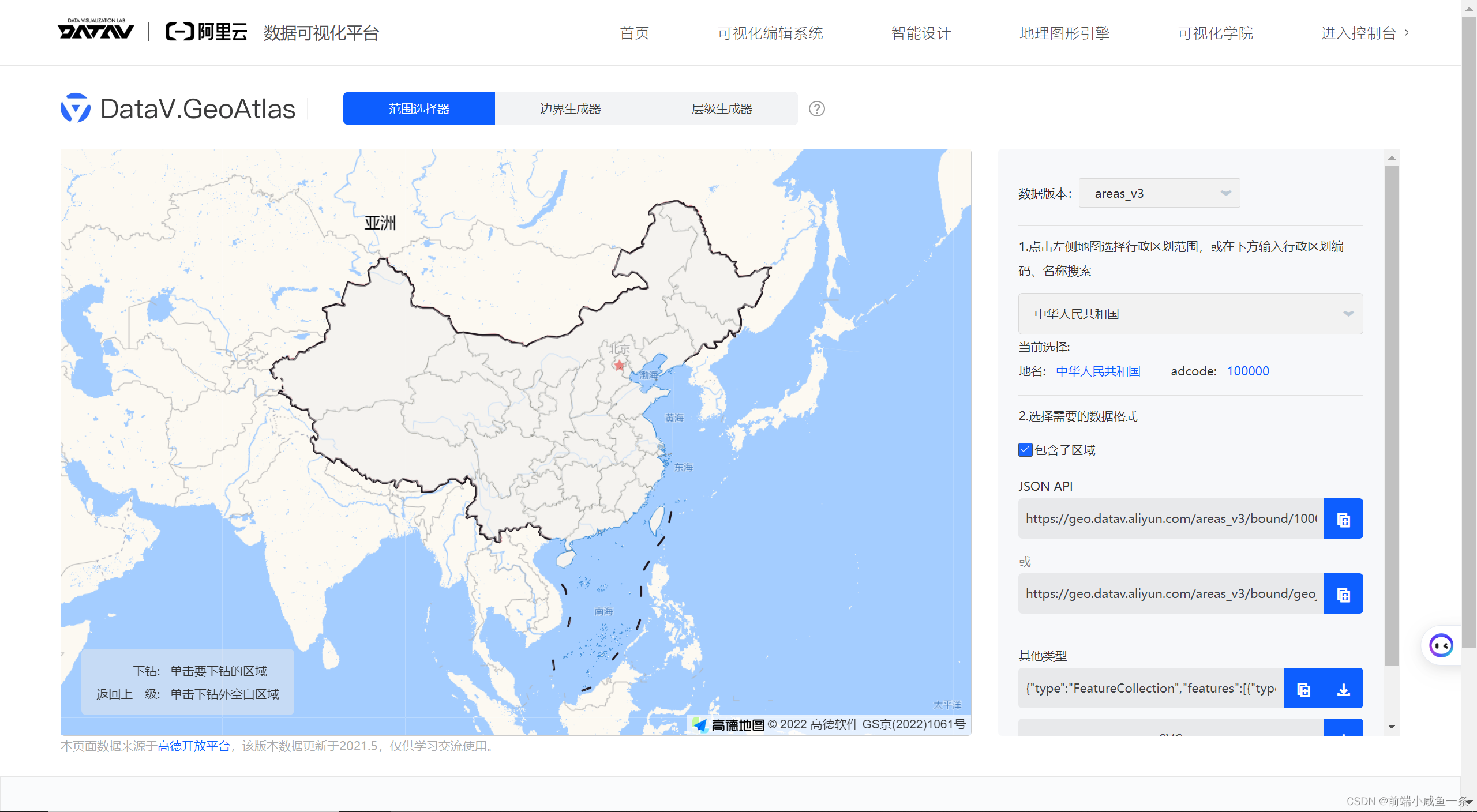
echart离线地图下载地址
链接: 离线地图地址 https://datav.aliyun.com/portal/school/atlas/area_selector...

elk日志某个时间节点突然搜索不到了
elk日志某个时间节点突然搜索不到了,检查filebeat正常 Kibana手动上传数据: 响应: Error: Validation Failed: 1: this action would add [2] total shards, but this cluster currently has [2000]/[2000] maximum shards open 原因:ElasticSearch总分片数量导致的异常,ES…...
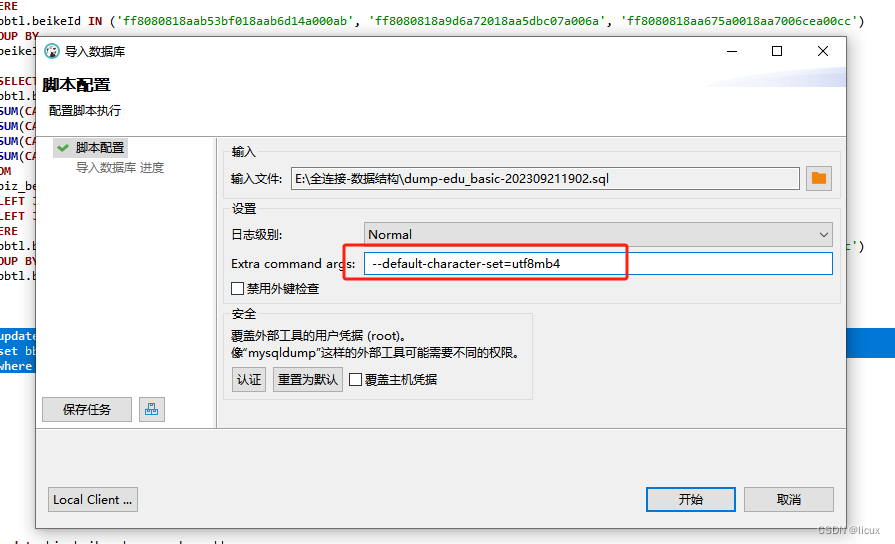
dbeaver 导出的sql文件,恢复数据库报错,Unknown command ‘\‘‘.
这是因为编码格式错误导致的, 加上这个即可 (注意前后不能有空格) --default-character-setutf8mb4...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
