四、数学建模之图与网络模型
1.定义
2.例题及软件代码求解
一、定义
1.图和网络是相关概念
(1)图(Graph):图是数学和计算机科学中的一个抽象概念,它由一组节点(顶点)和连接这些节点的边组成。图可以是有向的(有方向的,边有箭头表示方向)或无向的(没有方向的,边没有箭头表示方向)。图用于表示各种关系,如社交网络、电路、地图、组织结构等。
(2)网络(Network):网络是一个更广泛的概念,可以包括各种不同类型的连接元素,不仅仅是图中的节点和边。网络可以包括节点、边、连接线、路由器、服务器、通信协议等多种组成部分。网络的概念在各个领域都有应用,包括计算机网络、社交网络、电力网络、交通网络等。
2.图论的概念
(1)图:图是由一组节点(顶点)和连接这些节点的边组成的数学结构。图可以分为有向图和无向图,根据边是否有方向。
(2)顶点:顶点是图中的节点,它们可以代表不同的实体或对象。
(3)边:边是连接两个顶点的线段,它可以表示顶点之间的关系或连接。
(4)有向图:有向图是一种图,其中边有方向,从一个顶点指向另一个顶点。
(5)无向图:无向图是一种图,其中边没有方向,只表示两个顶点之间的连接。
(6)最小生成树问题:在一个连通图中,寻找一个包含所有顶点的子图,使得边的权重之和最小,被称为最小生成树问题。其中,Prim算法和Kruskal算法是解决这个问题的常用方法。
(7)路径:路径是图中一系列相邻的顶点,它们通过边相连。
(8)环:环是一条路径,起始点和结束点相同,形成一个闭合的循环。
(9)连通图:如果在无向图中,任意两个顶点之间都存在路径,那么这个图是连通的。对于有向图,可以有强连通图的概念。
(10)度数:一个顶点的度数是与它相邻的边的数量。在有向图中,分为入度和出度。
(11)图的表示:图可以用邻接矩阵、邻接表等不同方式来表示,这取决于需要进行的操作和问题类型。
(12)最短路径问题:寻找两个顶点之间最短路径的问题是图论中的一个经典问题,例如Dijkstra算法和Bellman-Ford算法。
3.稀疏矩阵表示法
一种用于有效存储和处理稀疏矩阵(大部分元素为零)的方法。在很多实际应用中,矩阵中的许多元素都是零,因此使用传统的密集矩阵表示法会浪费大量的存储空间和计算资源。稀疏矩阵表示法可以显著减少这种浪费。
常见的稀疏矩阵表示法
(1)压缩稀疏行表示法:在CSR表示法中,矩阵被分为三个数组:值数组(非零元素的值)、列索引数组(每个值对应的列索引)、行偏移数组(每行的起始位置在值数组中的索引)。这种表示方法适用于稀疏矩阵中的非零元素分散地分布在各行中的情况。
(2)压缩稀疏列表示法:与CSR类似,CSC也使用值数组、行索引数组和列偏移数组,但是列偏移数组表示每列的起始位置。CSC适用于稀疏矩阵中的非零元素分散地分布在各列中的情况。
(3)三元组表示法:在这种表示法中,矩阵的每个非零元素都由一个三元组 (行号、列号、元素值) 来表示。适用于初始构建稀疏矩阵或者非常稀疏的情况,但不太适用于高效的矩阵操作。
(4)对角线存储法:当稀疏矩阵具有对角线稀疏性(非零元素主要分布在对角线上)时,可以使用对角线存储法,只存储对角线及其附近的元素。
(5)块压缩表示法:对于某些特定应用,可以将矩阵分成块,并对每个块使用一种稀疏矩阵表示法。这对于一些科学计算和图像处理任务中的大型稀疏矩阵很有用。
二、例题(matlab或lingo求解)
1.矩阵表示有向图
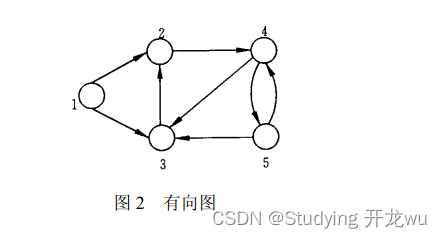

2.例 某公司在六个城市 中有分公司,从 到 的直接航程票价记在下述矩阵的 位置上。( 表示无直接航路),请帮助该公司设计一张城市 到其它城市间的票价最便宜的路线图。

clc,clear
a=zeros(6);
a(1,2)=50;a(1,4)=40;a(1,5)=25;a(1,6)=10;
a(2,3)=15;a(2,4)=20;a(2,6)=25;
a(3,4)=10;a(3,5)=20;
a(4,5)=10;a(4,6)=25;
a(5,6)=55;
a=a+a';
a(find(a==0))=inf;
pb(1:length(a))=0;pb(1)=1;index1=1;index2=ones(1,length(a));
d(1:length(a))=inf;d(1)=0;temp=1;
while sum(pb)<length(a)tb=find(pb==0);d(tb)=min(d(tb),d(temp)+a(temp,tb));tmpb=find(d(tb)==min(d(tb)));temp=tb(tmpb(1));pb(temp)=1;index1=[index1,temp];temp2=find(d(index1)==d(temp)-a(temp,index1));index2(temp)=index1(temp2(1));
end
d, index1, index2
3.例 在图 3 中,用点表示城市,现有 A, B1, B2 ,C1,C2 ,C3 , D 共 7 个城市。点与
点之间的连线表示城市间有道路相连。连线旁的数字表示道路的长度。现计划从城市 A到城市 D 铺设一条天然气管道,请设计出最小价格管道铺设方案。

编写 LINGO 程序如下:
model:
sets:
cities/A,B1,B2,C1,C2,C3,D/;
roads(cities,cities)/A B1,A B2,B1 C1,B1 C2,B1 C3,B2 C1,
B2 C2,B2 C3,C1 D,C2 D,C3 D/:w,x;
endsets
data:
w=2 4 3 3 1 2 3 1 1 3 4;
enddata
n=@size(cities); !城市的个数;
min=@sum(roads:w*x);
@for(cities(i)|i #ne#1 #and# i #ne#n:
@sum(roads(i,j):x(i,j))=@sum(roads(j,i):x(j,i)));
@sum(roads(i,j)|i #eq#1:x(i,j))=1;
@sum(roads(i,j)|j #eq#n:x(i,j))=1;
end
- 例无向图的最短路问题)求图 4 中 1 v 到 11 v 的最短路。
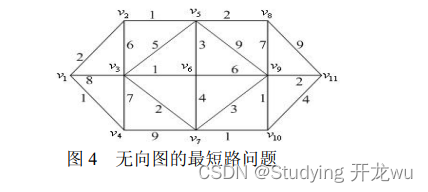
编写 LINGO 程序如下
:
model:
sets:
cities/1..11/;
roads(cities,cities):w,x;
endsets
data:
w=0;
enddata
calc:
w(1,2)=2;w(1,3)=8;w(1,4)=1;
w(2,3)=6;w(2,5)=1;
w(3,4)=7;w(3,5)=5;w(3,6)=1;w(3,7)=2;
w(4,7)=9;
w(5,6)=3;w(5,8)=2;w(5,9)=9;
w(6,7)=4;w(6,9)=6;
w(7,9)=3;w(7,10)=1;
w(8,9)=7;w(8,11)=9;
w(9,10)=1;w(9,11)=2;w(10,11)=4;
@for(roads(i,j):w(i,j)=w(i,j)+w(j,i));
@for(roads(i,j):w(i,j)=@if(w(i,j) #eq# 0, 1000,w(i,j)));
endcalc
n=@size(cities); !城市的个数;
min=@sum(roads:w*x);
@for(cities(i)|i #ne#1 #and# i #ne#
n:@sum(cities(j):x(i,j))=@sum(cities(j):x(j,i)));
@sum(cities(j):x(1,j))=1;
@sum(cities(j):x(j,1))=0; !不能回到顶点1;
@sum(cities(j):x(j,n))=1;
@for(roads:@bin(x));
end
相关文章:

四、数学建模之图与网络模型
1.定义 2.例题及软件代码求解 一、定义 1.图和网络是相关概念 (1)图(Graph):图是数学和计算机科学中的一个抽象概念,它由一组节点(顶点)和连接这些节点的边组成。图可以是有向的&…...

php在header增加key,sign,timestamp,实现鉴权
在PHP中,您可以通过在HTTP请求的Header中增加Key、Sign和Timestamp等信息来进行安全性鉴权。 以下是一种基本的思路和示例,用于说明如何实现这种鉴权机制: 生成Key和Sign: 服务端和客户端之间共享一个密钥(Key&#x…...
Spring实例化源码解析之ConfigurationClassParser(三)
前言 上一章我们分析了ConfigurationClassPostProcessor的postProcessBeanDefinitionRegistry方法的源码逻辑,其中核心逻辑do while中调用parser.parse(candidates)方法,解析candidates中的候选配置类。然后本章我们主要分析ConfigurationClassParser的…...

在 Substance Painter中实现Unity Standard Shader
由于有需要在Substance Painter中显示什么样的效果,在Unity就要显示什么样的效果的需求,最近研究了几天,总算在Substance Painter中实现Unity standard的材质的渲染效果。具体效果如下: 在Unity中: Substance Painte…...

第二证券:个人开证券账户要开户费吗?
随着互联网和移动端东西的遍及,越来越多的人开端涉足股票投资,开立证券账户也成为一个热门话题。但是,许多初学者或许会有疑问,个人开证券账户是否需求支付开户费呢?这个问题的答案并不是那么简略,需求考虑…...
大厂面试-16道面试题
1 java集合类有哪些? List是有序的Collection,使用此接口能够精确的控制每个元素的插入位置,用户能根据索引访问List中元素。常用的实现List的类有LinkedList,ArrayList,Vector,Stack。 ArrayList是容量…...
搭建GraphQL服务
js版 GraphQL在 NodeJS 服务端中使用最多 安装graphql-yoga: npm install graphql-yoga 新建index.js: const {GraphQLServer} require("graphql-yoga")const server new GraphQLServer({ typeDefs: type Query { hello(name:String):String! …...

数据仓库介绍及应用场景
数据仓库(Data Warehouse)是一个用于存储、管理、检索和分析大量结构化数据的集中式数据库系统。与传统的事务处理数据库不同,数据仓库是为了支持决策支持系统(Decision Support Systems, DSS)和业务智能(B…...
 LeetCode 583. 两个字符串的删除操作 72. 编辑距离)
代码随想录算法训练营Day56 | 动态规划(16/17) LeetCode 583. 两个字符串的删除操作 72. 编辑距离
动态规划马上来到尾声了,当时还觉得动态规划内容很多,但是也这么过来了。 第一题 583. Delete Operation for Two Strings Given two strings word1 and word2, return the minimum number of steps required to make word1 and word2 the same. In on…...
HTML+CSS+JavaScript 大学生网页设计制作作业实例代码 200套静态响应式前端网页模板(全网最全,建议收藏)
目录 1.介绍2.这样的响应式页面这里有200套不同风格的 1.介绍 资源链接 📚web前端期末大作业 (200套) 集合 Web前端期末大作业通常是一个综合性的项目,旨在检验学生在HTML、CSS和JavaScript等前端技术方面的能力和理解。以下是一些可能的Web前端期末大…...

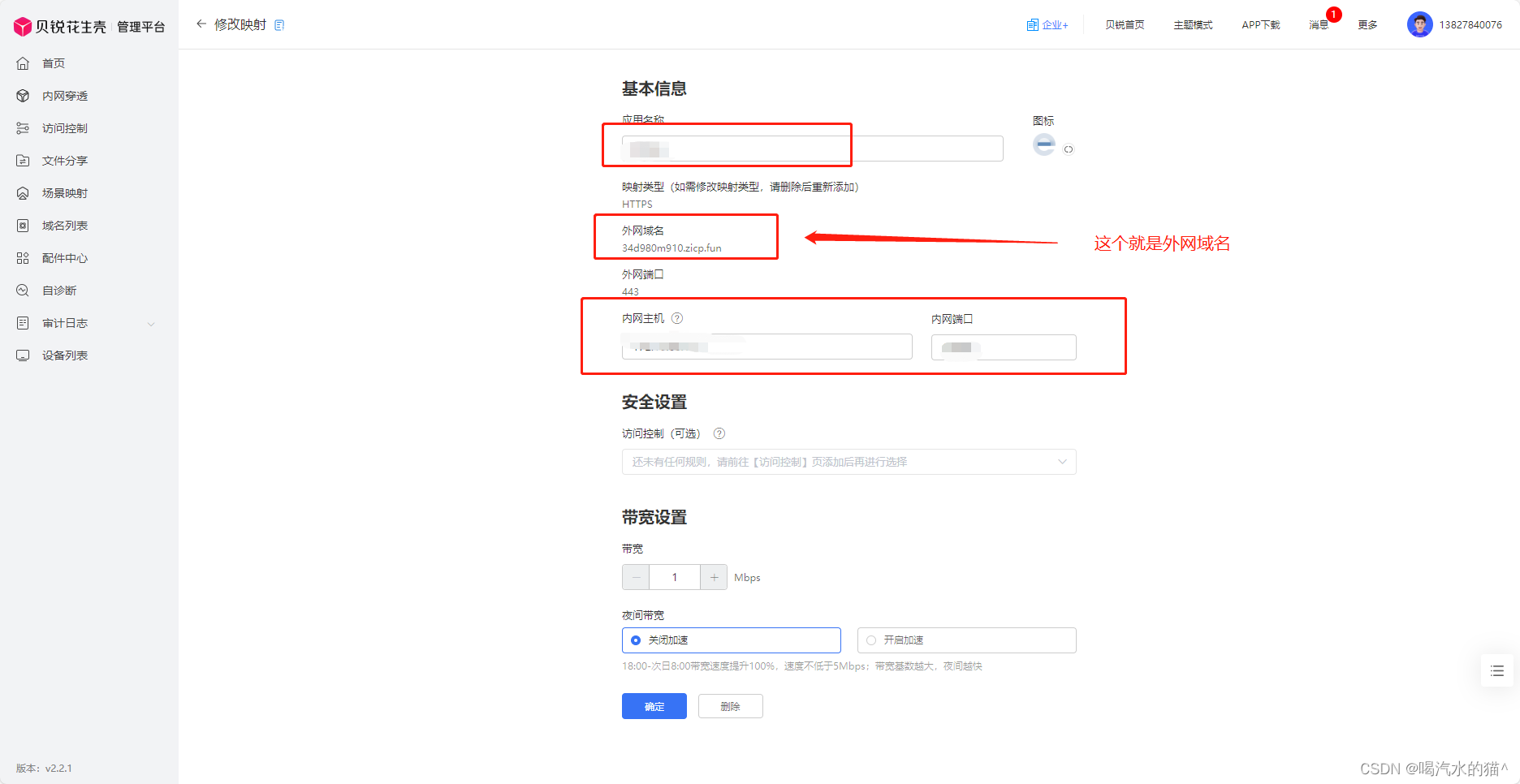
CFimagehost私人图床本地部署结合cpolar内网穿透实现公网访问
文章目录 1.前言2. CFImagehost网站搭建2.1 CFImagehost下载和安装2.2 CFImagehost网页测试2.3 cpolar的安装和注册 3.本地网页发布3.1 Cpolar临时数据隧道3.2 Cpolar稳定隧道(云端设置)3.3.Cpolar稳定隧道(本地设置) 4.公网访问测…...

uniapp瀑布流布局写法
首先我们要清楚瀑布流是什么? 瀑布流布局(Waterfall Flow Layout),也称为瀑布流式布局,是一种常见的网页或移动应用布局方式,特点是元素以不规则的方式排列,就像瀑布中的流水一样,每…...
蓝桥杯 题库 简单 每日十题 day8
01 扫雷 题目描述 在一个n行列的方格图上有一些位置有地雷,另外一些位置为空。 请为每个空位置标一个整数,表示周围八个相邻的方格中有多少个地雷。 输入描述 输入的第一行包含两个整数n,m。 第2行到第n1行每行包含m个整数,相邻整…...

Keepalived 高可用(附带配置实例,联动Nginx和LVS)
Keepalived 一、Keepalived相关知识点概述1.1 单服务的风险(单点故障问题)1.2 一个合格的集群应该具备的特性1.3 VRRP虚拟路由冗余协议1.4 健康检查1.5 ”脑裂“现象 二、Keepalived2.1 Keepalived是什么?2.2 Keepalived体系主要模块及其作用…...

第二证券:今年来港股回购金额超700亿港元 9月近200家公司获增持
本年以来,港股上市公司回购力度不断增强。据恒生指数公司计算,到9月15日,本年以来港股回购金额到达735亿港元,占去年全年总额的70%。该公司预测,2023年港股回购金额可能到达929亿港元,是前5年年度平均水平的…...

Autosar基础——RTE简介
AutoSAR文章目录 AUTomotive Open System Architecture Autosar-简介和历史发展 Autosar-软件架构 Autosar软件组件-Application Layer介绍和SWC(Software Component)类型 Autosar-Runnables(可运行实体) Autosar-OS配置 Autosar IOC机制(核间通信) Autosar实践-CANTp Auto…...

几个国内可用的强大的GPT工具
前言: 人工智能发布至今,过去了九个多月,已经成为了我们不管是工作还是生活中一个重要的辅助工具,大大提升了效率,作为一个人工智能的自然语言处理工具,它给各大行业的提供了一个巨大的生产工具,…...

《Python等级考试(1~6级)历届真题解析》专栏总目录
❤️ 专栏名称:《Python等级考试(1~6级)历届真题解析》 🌸 专栏介绍:中国电子学会《全国青少年软件编程等级考试》Python编程(1~6级)历届真题解析。 🚀 订阅专栏:订阅后可…...
在IntelliJ IDEA 中安装阿里P3C以及使用指南
在IntelliJ IDEA 中安装阿里P3C以及使用指南 1.关于阿里p3c1.1说明1.2什么是P3C插件1.3p3c的作用是什么 2 如何在IDEA中安装p3c2.1 插件安装2.2 插件使用 3.参考连接 1.关于阿里p3c 1.1说明 代码规范检查插件P3C,是根据《阿里巴巴java开发手册(黄山版)》转化而成的…...
Java集成支付宝沙箱支付,详细教程(SpringBoot完整版)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、开发前准备?二、使用步骤1、引入库2、配置在 application.yml 里面进行配置:3、alipay的java配置:AplipayConfig.java4、支付…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
