python/C++二分查找库函数(lower_bound() 、upper_bound,bisect_left,bisect_right)
二分查找是一种经典的搜索算法,广泛应用于有序数据集中。它允许在大型数据集中高效地查找目标元素,减少了搜索的时间复杂度。本文将介绍在 C++ 和 Python 中内置的二分查找函数,让二分查找变得更加容易。
c++
lower_bound() 、upper_bound
定义在<algorithm>头文件中,
lower_bound 和 upper_bound 是 C++ STL 中与二分查找相关的两个非常有用的函数。它们都用于在有序容器中查找元素的位置。下面我将通过一个示例来详细讲解它们的用法。
假设我们有一个有序的整数数组 arr,如下所示:
#include <iostream>
#include <vector>
#include <algorithm>int main() {std::vector<int> arr = {1, 2, 2, 3, 4, 4, 4, 5, 6, 7, 8, 9};int target = 4;// 使用 lower_bound 查找目标值的第一个出现位置std::vector<int>::iterator lower = std::lower_bound(arr.begin(), arr.end(), target);// 使用 upper_bound 查找目标值的最后一个出现位置的下一个位置std::vector<int>::iterator upper = std::upper_bound(arr.begin(), arr.end(), target);// 输出结果std::cout << "数组中 " << target << " 的出现位置:" << std::endl;std::cout << "lower_bound 的结果:" << std::distance(arr.begin(), lower) << std::endl;std::cout << "upper_bound 的结果:" << std::distance(arr.begin(), upper) << std::endl;return 0;
}在上述示例中,我们使用了 lower_bound 和 upper_bound 函数来查找目标值 4 在数组中的位置。下面是这两个函数的详细解释:
-
lower_bound:它返回一个迭代器,指向数组中第一个不小于目标值的元素。在我们的示例中,lower 将指向数组中第一个 4 的位置。
-
upper_bound:它返回一个迭代器,指向数组中第一个大于目标值的元素。在我们的示例中,upper 将指向数组中第一个大于 4 的元素位置。
请注意,如果目标值在数组中不存在,lower 和 upper 的差值将为零,因为它们将指向同一个位置。这两个函数在查找有序容器中的范围时非常有用,帮助我们精确定位元素的位置。
python
bisect_left
bisect.bisect_left(a, x, lo=0, hi=len(a), *, key=None)
bisect.bisect_left 函数在 Python 的 bisect 模块中用于在有序序列中查找目标值的插入位置,它接受四个参数:
a:表示有序序列,通常是一个列表。
x:表示要查找的目标值。
lo(可选):表示搜索范围的起始位置,默认为 0。
hi(可选):表示搜索范围的结束位置,默认为序列的长度。
下面是一个示例,演示了 bisect.bisect_left 函数的用法:
import bisectarr = [1, 2, 3, 4, 4, 4, 5, 6, 7, 8, 9]
target = 4# 在整个序列中查找目标值的插入位置
index = bisect.bisect_left(arr, target)
print(f"在整个序列中查找 {target} 的插入位置:{index}")# 在指定范围内查找目标值的插入位置
lo = 2 # 搜索范围的起始位置
hi = 7 # 搜索范围的结束位置
index_range = bisect.bisect_left(arr, target, lo, hi)
print(f"在范围 [{lo}, {hi}] 内查找 {target} 的插入位置:{index_range}")在上述示例中,首先我们在整个序列中查找目标值 4 的插入位置,然后在指定范围 [2, 7] 内查找 4 的插入位置。这两个插入位置的结果将告诉你如果将目标值插入到序列中,它应该出现在哪个位置。
bisect_right
bisect.bisect_right 函数与 bisect.bisect_left 函数非常类似,都用于在有序序列中查找目标值的插入位置。它们的区别在于,bisect_right 返回的位置是目标值插入后应该位于的右侧位置,而 bisect_left 返回的位置是目标值插入后应该位于的左侧位置。
相关文章:
 、upper_bound,bisect_left,bisect_right))
python/C++二分查找库函数(lower_bound() 、upper_bound,bisect_left,bisect_right)
二分查找是一种经典的搜索算法,广泛应用于有序数据集中。它允许在大型数据集中高效地查找目标元素,减少了搜索的时间复杂度。本文将介绍在 C 和 Python 中内置的二分查找函数,让二分查找变得更加容易。 c lower_bound() 、upper_bound 定义…...

爬虫 — App 爬虫(二)
目录 一、Appium介绍二、node.js 安装三、Java 的 SDK 安装以及配置1、安装步骤2、配置环境变量 四、安卓环境的配置1、配置环境变量 五、Appium 安装1、安装2、打开 APP3、使用 六、Appium 使用1、定位数据(方法一,不常用)2、定位数据&#…...
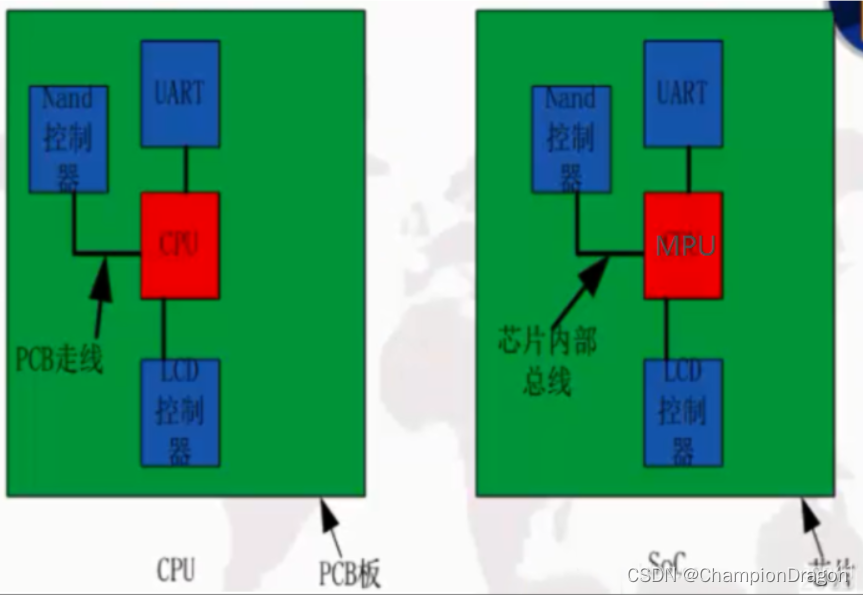
汽车电子相关术语
SOA SOA(Service-Oriented Architecture,面向服务的架构)是一种在计算机环境中设计、开发、部署和管理离散模型的方法。是由Garnter1996年提出的概念,将应用程序的不同功能单元(称为服务)进行拆分…...
Python 找出最大数
"""在输入的三个数中找出最大知识点:1、条件嵌套语句if/else2.字符串分割函数split()3、列表元素索引4、数据类型转换举一反三:1、如何控制只能输入三个数,否则重新输入2、如何避免输入无效字母"""# 定义一个变…...

Spring Security 用了那么久,你对它有整体把控吗?
文章目录 1.Servlet Filter:守门人的角色2.DelegatingFilterProxy:桥接 Servlet 和 Spring 的神器3.FilterChainProxy:Spring Security 过滤器链的管家3.SecurityFilterChain:Security 过滤器的串绳4.Spring Security 中的过滤器机…...

vue+minio实现文件上传操作
vueminio实现文件上传操作 minio文件上传vueminio实现文件上传操作 minio文件上传 minio文件上传有两种方法: 第一种是通过ak,sk,调用minio的sdk putObject进行文件上传;该方法支持go,java,js等各种语言&…...

使用JavaScript实现无限滚动的方法
前言 在网页设计中,无限滚动是一种常见的交互方式,用户可持续地加载更多内容而无需刷新页面,提高用户体验。本文将介绍如何运用JavaScript实现无限滚动的效果,使网页能够自动加载更多数据,减轻用户加载新页的负担&…...
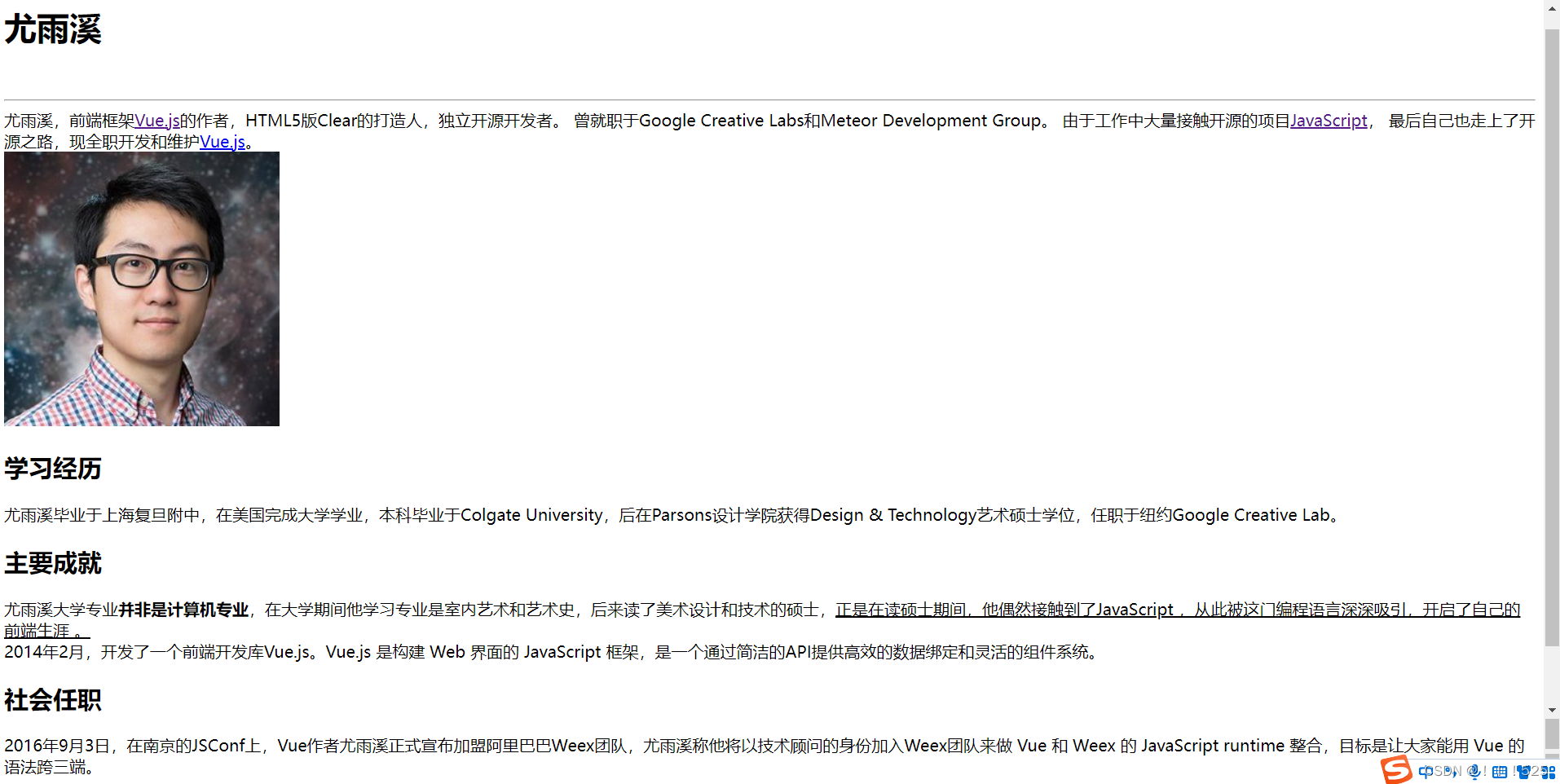
html学习综合案例1
<!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>个人简介</title> </head> <body>…...

神经节苷脂抗体——博迈伦
神经节苷脂抗体是指人体免疫系统中产生的一类抗体,其主要作用是攻击神经节苷脂抗原物质。神经节苷脂是一种存在于神经细胞表面的重要分子,参与了神经细胞间的信号传导和细胞黏附等重要功能。正常情况下,人体免疫系统不会对神经节苷脂产生抗体…...
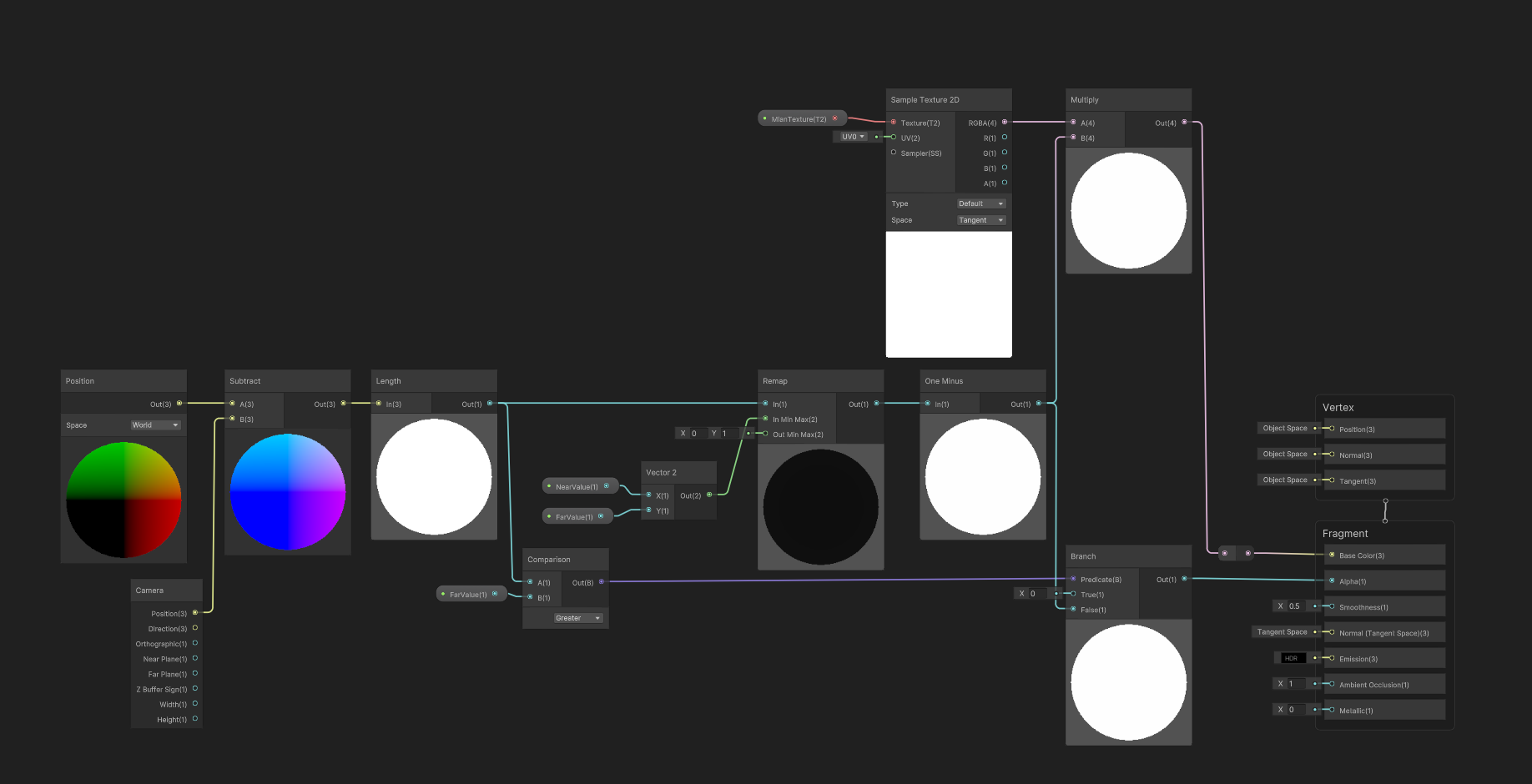
【Unity】简单的深度虚化shader
【Unity】简单的深度虚化shader 实现效果 可以用于对地图场景边界的白模处理 实现方法 1.关键方法 UnityObjectToClipPos:将物体坐标转换为屏幕坐标 LinearEyeDepth:将屏幕坐标中的z值转换为实际的深度值 saturate:将值规范到0~1之间&a…...

启动 React APP 后经历了哪些过程
本文作者为 360 奇舞团前端开发工程师 前言 本文中使用的React版本为18,在摘取代码的过程中删减了部分代码,具体以源代码为准。 在React 18里,通过ReactDOM.createRoot创建根节点。并且通过调用原型链上的render来渲染。 本文主要是从以下两个…...

带自动采集小说网站源码 小说听书网站源码 小说网站源码 带教程
PTCMS可听书可下载的小说站源码 带自动采集和搭建视频教程 必装环境:Nginx(apache.iis也可),mysql,php5.6,memcached php5.6安装扩展memcache新建站点,注意新建时,PHP版本必须选择PHP5.6 安装教程 1.上传网站文件到网站目录&…...
MySQL学习笔记2
MySQL glibc版本安装: 下载相应的安装包。 学会查看mysql的官方文档: 1) 2)点击“Reference Manual”按钮: 3)选择5.7版本: 4)点击Installing MySQL on Unix/Linux Using Generic …...

【python爬虫】—星巴克产品
文章目录 需求爬取星巴克产品以及图片,星巴克菜单 python爬虫爬取结果 需求 爬取星巴克产品以及图片,星巴克菜单 网页分析: 首先,需要分析星巴克官方网站的结构,了解菜单栏的位置、布局以及菜单项的标签或类名等信息…...
)
算法 矩阵最长递增路径-(递归回溯+动态规划)
牛客网: BM61 求矩阵的最长递增路径 解题思路: 1. 遍历二维矩阵每个位置,max求出所有位置分别为终点时的最长路径 2. 求某个位置为终点的最长路径时,使用动态规划dp对已经计算出的位置进行记录 3. 处理某个位置的最长路径时,如果dp[i][j]位…...
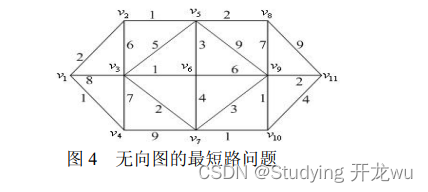
四、数学建模之图与网络模型
1.定义 2.例题及软件代码求解 一、定义 1.图和网络是相关概念 (1)图(Graph):图是数学和计算机科学中的一个抽象概念,它由一组节点(顶点)和连接这些节点的边组成。图可以是有向的&…...

php在header增加key,sign,timestamp,实现鉴权
在PHP中,您可以通过在HTTP请求的Header中增加Key、Sign和Timestamp等信息来进行安全性鉴权。 以下是一种基本的思路和示例,用于说明如何实现这种鉴权机制: 生成Key和Sign: 服务端和客户端之间共享一个密钥(Key&#x…...
Spring实例化源码解析之ConfigurationClassParser(三)
前言 上一章我们分析了ConfigurationClassPostProcessor的postProcessBeanDefinitionRegistry方法的源码逻辑,其中核心逻辑do while中调用parser.parse(candidates)方法,解析candidates中的候选配置类。然后本章我们主要分析ConfigurationClassParser的…...

在 Substance Painter中实现Unity Standard Shader
由于有需要在Substance Painter中显示什么样的效果,在Unity就要显示什么样的效果的需求,最近研究了几天,总算在Substance Painter中实现Unity standard的材质的渲染效果。具体效果如下: 在Unity中: Substance Painte…...

第二证券:个人开证券账户要开户费吗?
随着互联网和移动端东西的遍及,越来越多的人开端涉足股票投资,开立证券账户也成为一个热门话题。但是,许多初学者或许会有疑问,个人开证券账户是否需求支付开户费呢?这个问题的答案并不是那么简略,需求考虑…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

初探用uniapp写微信小程序遇到的问题及解决(vue3+ts)
零、关于开发思路 (一)拿到工作任务,先理清楚需求 1.逻辑部分 不放过原型里说的每一句话,有疑惑的部分该问产品/测试/之前的开发就问 2.页面部分(含国际化) 整体看过需要开发页面的原型后,分类一下哪些组件/样式可以复用,直接提取出来使用 (时间充分的前提下,不…...

C/Python/Go示例 | Socket Programing与RPC
Socket Programming介绍 Computer networking这个领域围绕着两台电脑或者同一台电脑内的不同进程之间的数据传输和信息交流,会涉及到许多有意思的话题,诸如怎么确保对方能收到信息,怎么应对数据丢失、被污染或者顺序混乱,怎么提高…...

组合模式:构建树形结构的艺术
引言:处理复杂对象结构的挑战 在软件开发中,我们常遇到需要处理部分-整体层次结构的场景: 文件系统中的文件与文件夹GUI中的容器与组件组织结构中的部门与员工菜单系统中的子菜单与菜单项组合模式正是为解决这类问题而生的设计模式。它允许我们将对象组合成树形结构来表示&…...
